基于多种群搜索的PSO的物流配送中心寻址求解

李 磊, 杨爱峰, 唐 娜, 陈亚波

(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.过程优化与智能决策教育部重点实验室,安徽 合肥 230009)

基于多种群搜索的PSO的物流配送中心寻址求解

李 磊1,2, 杨爱峰1,2, 唐 娜1,2, 陈亚波1,2

(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.过程优化与智能决策教育部重点实验室,安徽 合肥 230009)

物流配送中心选址不仅影响运输等成本,而且也影响顾客的服务水平,在现代物流中具有重要的现实意义。针对物流配送中心选址问题,文章提出了一种基于改进粒子算法的智能求解方法，建立了物流配送中心选择模型,根据模型特点设计出了与免疫优化算法混合的粒子群算法、多种群搜索策略、混沌初始化方法、多样性评价方法。通过合理地设置算法参数,对物流配送中心选址问题进行实验比较,实验结果表明,该文算法的求解效果良好,并且求解的速度较快。

物流配送中心选址;粒子群算法;多种群;混沌;精英子群

粒子群优化算法[1](particle swarm optimization,PSO)是1995年美国学者Eberhart E C和Kennedy J提出的一种群智能优化算法。PSO算法具有参数少、收敛速度快的优点[2],但是同时也具有容易陷入局部解的缺点,而且基本PSO算法主要是用来解决连续性问题的一种算法,要应用到离散问题或者组合优化问题则要进行相应的设置和改进。目前主要用于解决离散化问题的PSO算法主要有如下3种:① 对PSO算法解的表现形式和更新公式进行重新定义,如二进制PSO算法[3]等;② 不改变PSO算法的形式,仍然使用基本PSO算法进行求解,只是在求解的最后将所得解取整;③ 将PSO算法与离散化的算法进行混合求解,如与遗传算法混合的PSO算法[4]、与蚁群算法混合的PSO算法[5]、模拟退火粒子群优化算法[6]、基于粒子群优化的电动汽车再生制动模糊控制[7]等。

物流配送中心选址问题[8]是典型的组合优化问题,由于它是一个整数规划,且变量及相关约束非常多,属于典型的NP难问题,找到多项式计算时间内的解非常困难。传统的求解方法有重心法、拉格朗日松弛法、分支定界法等。其中重心法主要用于单一配送中心选址模型;拉格朗日松弛法往往可以获得中等规模问题的次优解,但其性能依赖于问题本身结构;分支定界法能获得问题的全局最优解,但随着问题规模增加求解效率低下,适合一些小规模简单模型。近年来由于启发式随机优化方法在复杂优化问题中的广泛应用,为物流配送中心选址问题提供了新的思路,比如遗传算法、免疫优化算法、粒子群算法等。

1 免疫优化算法

生物免疫系统是一个高度进化的生物系统,旨在区分外部有害抗原和自身组织,从而保持有机体的稳定。从计算角度看,生物免疫系统是一个高度并行、分布、自适应和自组织的系统,具有很强的学习、识别和记忆能力。

免疫优化算法[9](immune optimization algorithm,IOA)是在遗传算法的基础上发展起来的。它模拟生物免疫系统对外来抗原的排除,借鉴免疫系统的自组织学习、自适应调节的特点,在保留遗传算法优良特性的前提下,力图有选择、有目的地利用待求问题中的一些特征信息或知识来抑制其优化过程中出现的退化现象,具有免疫记忆特性、抗体自我识别能力和免疫多样性的特点,但与遗传算法一样,它仍不能充分利用求解问题的特征信息指导全局搜索,搜索是盲目的、随机的,在小区域仍不能克服不成熟收敛现象,在小空间搜索效率并不显著。免疫算法与遗传算法类似,采用群体搜索策略,并且强调群体中个体间的信息交换。但免疫算法评价个体的标准不是适应度,而是亲和度,因此免疫算法对个体的评价更加合理。

免疫优化算法的优化过程如下:

(1) 分析问题。对问题及其解的特性进行分析,设计解的合适表达形式。

(2) 产生初始抗体群。随机产生N个个体并从记忆库中提取m个个体构成初始群体,其中,m为记忆库中个体的数量。

(3) 对上述群体中各个抗体进行评价。在本算法中对个体的评价是以个体的期望繁殖概率为标准的。

(4) 形成父代群体。将初始群体按期望繁殖概率进行降序排序,并取前N个个体构成父代群体;同时取前m个个体存入记忆库中。

(5) 判断是否满足结束条件,是则结束;反之,则继续下一步操作。

(6) 新群体的产生。基于步骤(4)的计算结果对抗体群进行选择、交叉、变异操作得到新群体,再从记忆库中取出记忆的个体,共同构成新一代群体。

2 基于多种群搜索的粒子群算法

2.1 基本粒子群算法

粒子群算法[10]中每个潜在解都代表一个粒子,每个粒子对应一个适应度值,每个粒子都有一个表示移动方向的速度和位置。粒子在解空间中运动,通过跟踪个体极值Pbest和群体极值Gbest更新个体位置。

设在一个D维搜索空间中,n个粒子组成的种群X=(X1,X2,…,Xn),其中Xi=(xi1,xi2,…,xiD)T,代表第i个粒子在D维搜索空间中的位置,即一个潜在解。Vi=(vi1,vi2,…,viD)T,代表第i个粒子在D维搜索空间中的移动速度,其个体极值为pi=(pi1,pi2,…,piD)T,种群的群体极值为g=(g1,g2,…,gD)T。粒子的速度位置更新公式如下:

(1)

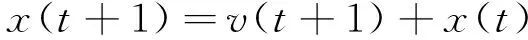
(2)

其中,c1、c2为非负的常数,称为学习因子;r1、r2为分布于[0,1]的随机数。

2.2 基于多种群搜索的粒子群算法

2.2.1 粒子群的初始化

本文算法(MSPSO)用粒子的位置变量来表示离散问题的可行解,采用整数编码的方式,每个粒子用length维向量表示。混沌[11]是自然界广泛存在的一种非线性现象,具有随机性、遍历性和规律性的特点,现在已被广泛地运用到随机优化问题中。

为了提高算法搜索的效率,在粒子群初始化时将粒子均匀分布在解空间中,可以扩展可行解的搜索范围,有助于提高求解的效率和质量,因此,本文将混沌引入到粒子的初始化当中。Logistic混沌映射模型的定义如下:

(3)

(4)

其中,maxAk、minAk为区间Ak的最大值和最小值；[]为取整符号。

2.2.2 粒子的多样性评价

粒子的多样性评价反映了粒子之间的相似程度,主要吸取了免疫优化算法中抗体间亲和度的计算方法。

定义1(粒子间的相似度) 粒子间的相似度反映了2个粒子之间的相似程度,此处借鉴免疫优化算法中抗体间亲和度的计算方法。粒子采用整数编码的方式,假设粒子是length维空间上的点,则粒子间的相似度表示为:

Sij=lij/length

(5)

其中,i=1,2,…,N,j=1,2,…,N,N为种群中粒子的数目;Sij为粒子i与粒子j的分量取值相等的个数lij占粒子维数length的比例。

定义2(粒子与种群的相似程度) 粒子与种群的相似程度指的是粒子分别与种群中其余粒子之间的相似度大于某个阈值的个数与种群大小的比例,即

(6)

其中,T为预先设定的某个值;i=1,2,…,N,j=1,2,…,N,N为种群中粒子的数目。

定义3(粒子的多样性参数) 粒子在种群中的多样性评价参数是由粒子的适应度值和粒子与种群的相似程度共同决定的,即

(7)

其中,i=1,2,…,N,j=1,2,…,N,N为种群中粒子的数目;fi为粒子i的适应度值的倒数;α∈(0,1)。

(7)式表明：若粒子的适应度值越好,则多样性越好;若粒子与群体相似程度越高,则多样性越低。这样就促进了适应度好的粒子,同时也抑制了多样性不好的粒子。

2.2.3 种群搜索策略

在初始化种群后,将种群分成pop1和pop2 2个子群,子群pop2进行精确搜索,而子群pop1则辅助pop2进行探索式搜索。

子群pop1中的每个粒子分别与自身的极值pbest交叉,这样每个粒子都分别跟踪不同的历史极值进行更新,不仅能够保持该子群的多样性,而且还能进行全局的搜索,之后通过适当的选择进行变异操作以进行局部的搜索,确保更加准确的搜索。

子群pop2中的粒子与精英子群中随机选择的粒子best进行交叉操作,这样可以产生更多优秀的粒子,之后同样进行适当的变异操作,确保对优秀个体的局部进行搜索。而精英子群elite的形成是将适应度值较好的粒子和根据(7)式计算得到的粒子组合成的一个子群。

2个子群间的信息交流是单向交流,pop1通过在搜索过程中得到的种群极值保留在elite中来向pop2传递信息,算法搜索策略及子群间的信息交流方式如图1所示。

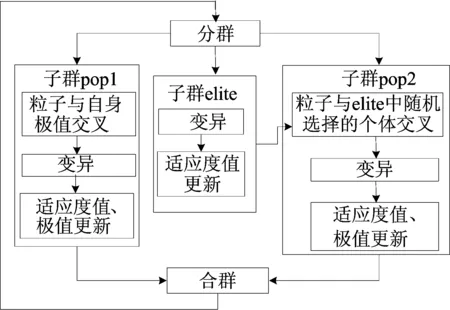
图1 算法的搜索策略及子群间的信息交流

粒子与历史极值和优秀个体进行交叉分别表示为:

p(t)=p(t)⊗pbest(t)

(8)

(9)

其中,p(t)为群体中的一个粒子;pbest(t)为这个粒子的历史极值;best(t)为随机从子群elite中选中的一个粒子,这样每个粒子追求不同的极值进行迭代,能维持种群的多样性加快收敛速度;⊗为交叉操作,这里采用单点交叉法。

为了在迭代过程中保留较好的粒子,对子群elite主要进行局部的精确搜索,这里采用随机变异位变异的方法。

2.2.4 算法流程

(1) 分析问题。对问题及其解的特性进行分析,设计解的合适表达形式。

(2) 参数设置。设置种群大小N、子群大小n1和n2、最大迭代次数Maxiter、精英子群大小m、解的长度length和多样性评价参数D。

(3) 产生初始解。利用(3)式与(4)式混沌初始化粒子群。

(4) 分群。首先,把种群中适应度值最优的粒子加入到精英子群中,然后利用(5)～(7)式将多样性较好的粒子加入到精英子群中。其次,将群体划分为2个子群pop1和pop2。

(5) 子群更新。在子群pop1中,粒子分别与自身极值交叉,然后进行选择变异,最后计算适应度值;在子群pop2中,粒子与在精英子群中随机选择的优秀粒子进行交叉,然后进行选择变异,最后计算适应度值。

(6) 精英子群搜索操作。对精英子群进行局部变异搜索是为了精确地搜索优秀个体的局部潜在的最优解。

(7) 合群。将子群pop1与子群pop2重新组合成一个群体。

(8) 判断是否满足结束条件,是则结束;否则跳到步骤(4)继续执行。

3 物流配送中心选址问题求解

3.1 物流配送中心选址模型

物流配送中心选址模型[12]中有如下假设:

(1) 配送中心的规模容量总可以满足需求点的需求,并由其配送辐射范围内的需求量确定。

(2) 一个需求点仅由一个配送中心供应。

(3) 不考虑工厂到配送中心的运输费用。

基于以上假设建立模型，该模型是一个选址/分配模型,在满足距离上限的情况下,需要从M个备选配送中心中找出m个配送中心向n个需求点配送物品。目标函数是各配送中心到需求点的运费与配送中心固定建设费用之和最小。规划模型如下:

(10)

(11)

(12)

(13)

(14)

(15)

其中,N={1,2,…,n}为所有需求点的序号集合;Mi为到需求点i的距离小于s的备选配送中心集合;s为新建配送中心离由其服务的需求点的距离上限;v为单位产品单位距离的运输费用(即运费率);wi为需求点的需求量;dij为从需求点i到离其最近的配送中心j的距离;Cj为配送中心的固定建设成本;p为从候选点选出的配送中心总和;Zij为0-1决策变量,表示用户和物流中心的服务需求分配关系,当其为1时,表示需求点i的需求量由配送中心j供应,否则Zij=0;hj为0-1决策变量,当其为1时,表示候选点j被选为配送中心,否则hj=0。

(10)式表示各配送中心到需求点的运费与配送中心固定建设费用之和;(11)式表示每个需求点只能由一个配送中心送货;(12)式表示若候选的配送中心没有被选中,则从该配送中心不能供应任何需求点,否则可以供应;(13)式表示从配送中心到需求点运输距离不超过s;(14)式表示从候选点选出的配送中心总和等于p;(15)式表示决策变量的0-1约束。

3.2 问题求解

本文算法采用整数编码的方式,根据实际问题的需要,每个粒子都是维数为length(配送中心的数目)的可行解,代表被选为配送中心的需求点序列,例如:粒子[3 2 8 12 5 9]代表序号为3、2、8、12、5和9的城市被选为配送中心。针对上述配送中心选址模型得到的粒子适应度值函数为:

(16)

现在要从12个候选配送中心城市中选取出6个城市作为配送中心来给需求点城市配送物资,使得总的运输成本最小。为了简化实验,将城市间的距离作为运输费用,单位物资的成本为1。

21个需求点城市的空间位置和物资需求量见表1所列。

候选配送中心城市的空间位置和建设费用见表2所列。

表1 需求点位置及其物资需求量 t

表2 候选配送中心城市的位置坐标及建设成本 万元

3.3 实验结果分析

本文的实验环境为:硬件环境采用32位Windows7操作系统、I5CPU、4GB内存;软件环境采用matlabr2012a。

本文的实验参数设置为:种群规模为80、2个子群大小均为40、精英子群的大小为10、最大迭代次数为200。

在实验参数相同的条件下,将本文算法与PSO[13]、IOA[14](internetofficeautomation)和HPSO[15](harmonionsparticleswarmoptimizer)进行仿真实验得到的结果进行比较。

问题模型的最优解方案为[1 8 6 4 2 7],该方案表示候选配送中心城市序号分别为1、8、6、4、2和7的6个候选配送城市被选为配送中心,作为给需求点配送物资的配送点,且这个方案的最小的配送费用为581 663.859 450 40,该最优配送方案如图2所示。

图2中25个空心圆圈表示的是25个需求点城市,12个实心圆是候选配送中心城市,而正方形中间的实心圆圈是选中的配送中心城市,与各个配送点有连线的空心圆圈表示圆圈所代表的需求点由这个配送中心配送物资。

在实验过程中,4种算法通过迭代寻优都能够找到这个模型的最优解,因此得到的最优方案与图2中的方案一致。

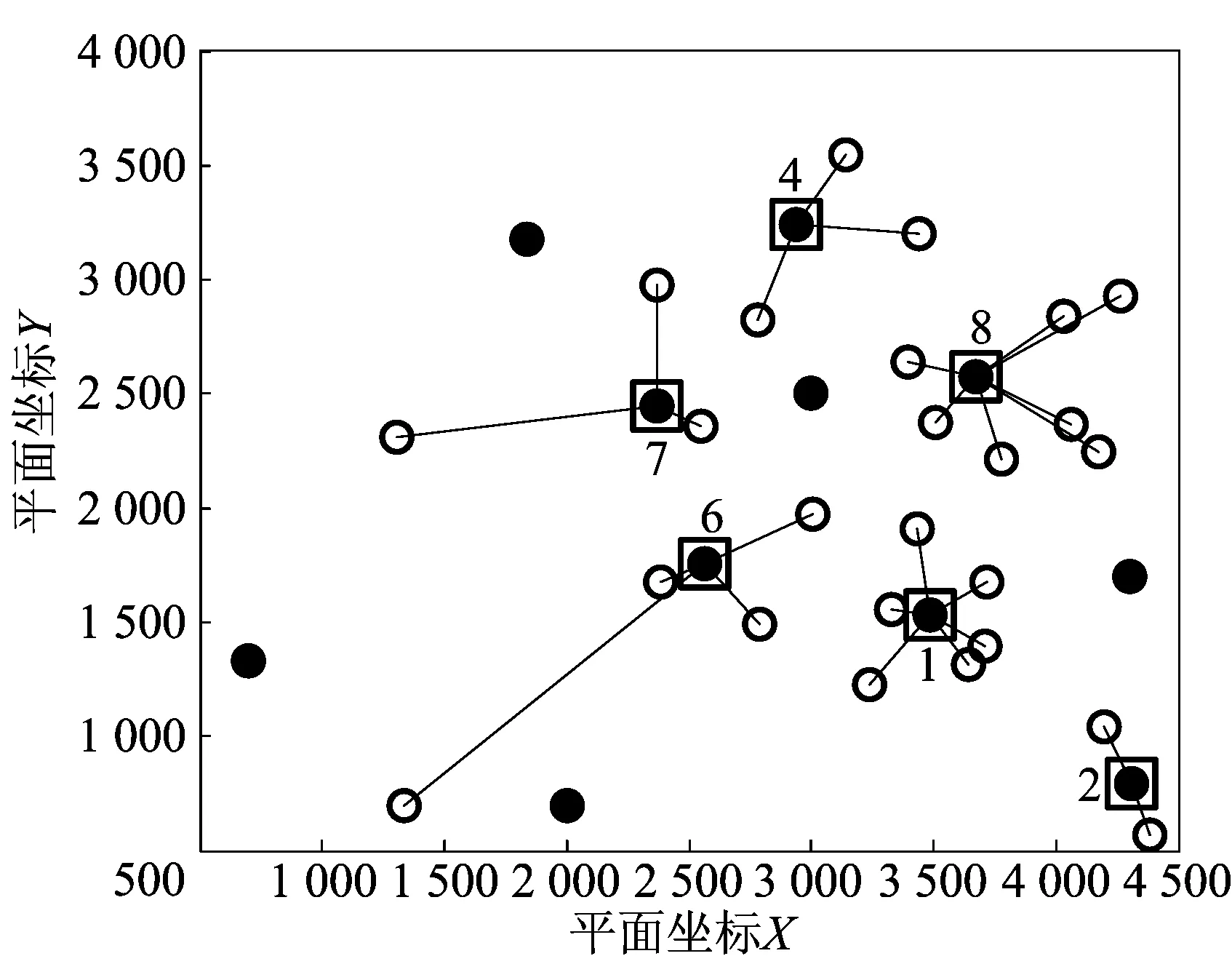
图2 最优配送方案

4种算法迭代的收敛曲线如图3所示。从图3中可以看出4种算法都能收敛到最优解。其中,本文算法MSPSO收敛速度比IOA和HPSO算法的收敛速度快,但是要比PSO算法的收敛速度慢。

图3 4种算法的收敛曲线

程序独立运行20、30、50次时算法得到的最优解次数折线图如图4所示。

从图4a中可以看出,基本粒子群算法PSO得到最优解的次数最少,其次是免疫优化算法IOA、混合粒子群算法与本文算法得到的最优解次数是最多的。

从图4b中可以看出,本文算法得到最优解的次数要比PSO、IOA和MPSO算法得到最优解次数都要多。

从图4c中可以看出本文算法得到的最优解次数是最多的,比PSO、IOA和MPSO算法得到的最优解次数都要多。

图4 程序独立运行20、30、50次时算法得到的最优解次数

综上所述,PSO算法在求解该问题时最不稳定、寻优的概率最低,IOA算法和HPSO算法在寻优的过程中得到最优的概率则比较稳定,但是得到最优解的概率也没有本文算法的高,而本文算法MSPSO寻找最优解的概率是最大的,从而证明了本文算法在求解物流配送中心选址问题时具有良好的效果及稳定性。

4 结 论

针对物流配送中心选址问题,本文提出了基于多种群搜索策略的混合粒子群优化算法。结果表明，本文算法在求解物流配送中心选址问题中具有较好的搜索能力,并且搜索的性能也较优,证明了本文算法在求解离散化的问题方面有着较好的能力。在本文算法中,提出了一种利用混沌初始化种群个体的方法,使粒子能够均匀分布在问题空间中,提高了搜索到最优解的概率,同时把混沌引入到解决离散问题的算法更新中将是下一步的研究工作。

[1] LABAL N,ZERGUINE A,AL-DHAHIR N.Decision feedback equalization using particle swarm optimization[J].Signal Processing,2015,108:1-12.

[2] 李丽,牛奔.粒子群优化算法[M].北京:冶金工业出版社,2010:123-124.

[3] 王志刚,夏慧明,王明刚,等.求解多维背包问题的改进二进制粒子群算法[J].数学的实践与认识,2013,43(19):129-137.

[4] 刘快,纪志成.基于混合粒子群的RFID网络的优化部署[J].计算机应用研究,2012,29(4):1326-1328.

[5] 徐青鹤,刘士荣,吕强.基于蚁群混沌行为的离散粒子群算法及其应用 [J].计算机科学,2010,37(5):178-180.

[6] 刘志峰,杨德军,顾国刚.基于模拟退火粒子群优化算法的拆卸序列规划[J].合肥工业大学学报(自然科学版),2011,34(2):163-165,179.

[7] 周云鹏,赵韩,江昊.基于粒子群优化的电动汽车再生制动模糊控制[J].合肥工业大学学报(自然科学版),2014,37(7):771-772.

[8] 王志刚,王明刚,尚旭东.基于人工蜂群算法的配送中心选址问题求解[J].数学的实践与认识,2014, 44(17):170-175.

[9] 戚玉涛,刘芳,常伟远,等.求解多目标问题的Memetic的免疫优化算法[J].软件学报,2013,24(7):1529-2544.

[10] 朱大林,詹腾,张屹,等.多策略差分进化的元胞多目标粒子群算法[J].电子学报,2014,42(9):1831-1838.

[11] YANG Zuyuan,YANG Huafen,YANG You,et al.An improved particle swarm optimization method based on chaos.[C]//2014 10th International Conference on Natural Computation.[S.l.]:IEEE,2014:209-213.

[12] 史峰,王辉,郁磊,等.Matlab 智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011:118-120.

[13] 赵莉,董玉民.基于量子遗传的混合粒子群优化算法[J].计算机工程与设计,2014,35(7):2566-2571

[14] 李贞双,李争艳.基于云模型的量子免疫优化算法[J].计算机工程与应用,2011,47(21):123-125.

[15] GHAMISI P,BENDIKTSSON J A.Feature selection based on hybridization of genetic algorithm and particle swarm optimization[J].IEEE Geoscience and Remote Sensing Letters,2015,12(2):309-313.

(责任编辑 张 镅)

Solution for logistics distribution center location based on multi-population search PSO algorithm

LI Lei1,2, YANG Aifeng1,2, TANG Na1,2, CHEN Yabo1,2

(1.School of Management, Hefei University of Technology, Hefei 230009, China; 2.Key Laboratory of Process Optimization and Intelligent Decision Making of Ministry of Education, Hefei 230009, China)

Logistics distribution center location not only decides the cost such as transportation cost, but also impacts the customer service level. It has important practical significance in modern logistics. For solving this logistics distribution center location problem, an improved particle swarm optimization(PSO) based intelligent optimization algorithm is proposed. Firstly, the mathematical model of the logistics distribution center location is set up. And for solving it, the PSO hybridized with immune optimization algorithm(IOA), multi-population search strategy, chaos initialization method and diversity evaluation method are designed. By setting parameters reasonably, the experiments are conducted and the results show that the proposed algorithm has better solving performance and rapid solving speed.

logistics distribution center location; particle swarm optimization(PSO); multi-population; chaos; elite-subgroup

2015-11-16；

2016-01-14

国家自然科学基金青年科学基金资助项目(71301038;71301041)

李 磊(1990-),男,湖北武汉人,合肥工业大学硕士生; 杨爱峰(1976-),女,河南濮阳人,博士,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.02.024

TP18

A

1003-5060(2017)02-0266-06