心磁信号插值处理的相关性研究
陈 浩, 陈 波, 李 华, 储昭碧, 孔 艳
(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)
心磁信号插值处理的相关性研究
陈 浩, 陈 波, 李 华, 储昭碧, 孔 艳
(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)
插值是丰富离散数据有效的方法,文章在构建心磁相关序列的基础上,研究了离散心磁数据插值前后的相关性,将统计学秩和检验引入来判断系统是否有显著性差别,并在频域范围内,对插值前后数据进行解析。经过相关性和统计学秩和检验分析后,得出插值前后的数据系统存在具体的联系,证实插值前后的数据没有显著差别,并且插值前后的心磁数据保持了相关系数、方差、峰度、幅频波形的一致性。因此插值是丰富心磁医学数据的有效方法。
相关性;插值;心磁数据
综合国内外对心磁信号的研究可知,通过超导量子干涉仪(superconducting quantum interference device,SQUID)测量获得的心磁数据是反映心脏磁场变化的一种非准周期性的非平稳信号,它包括了大量的心脏生理信息。由于硬件SQUID条件所限,在检测人体心脏表面磁场时采用分时分块采点法,即在心脏表面上检测20 cm×20 cm区域中36个点上的磁场数据。根据探头测量通道个数不同,在每时刻只能同时采集到与通道数量相同的点,例如4通道SQUID在每采集时刻内同时采集2×2个点上的磁场数据,分时采集9次得到人体心脏磁场表面6×6个点的心脏磁场数据[1-2]。
研究心磁场分布时这36个点的数据作为绘制MFM填充图和心脏电流密度分布图的唯一信息,若心磁测量设备能提供大量的、密集的心磁空间点数据,则可以得到精确度高的信息,得到更高质量的图像。但是由于测量设备的限制,实际通过SQUID测得的数据不但是离散数据而且还是有限的,通过科学计算来增加合理的点数,用以丰富数据系统,有利于心磁数据的进一步处理和分析。插值是丰富离散数据有效的方法,插值的目的是依据实测得到的采样数据,在更高的精度下“恢复”原来的连续信号[3-5]。对心磁数据进行插值处理,通过分析计算增加符合条件的点数,可以丰富数据系统。但必须对插值前后心磁数据的相关性进行分析,明确插值对医学信息不一致的可能性。本文研究了实测心磁数据插值前、后的相关性,为正确使用插值理论方法提供依据和理论基础。样条插值是最佳的插值函数模型,具有光滑的性质;而线性插值是最简单的插值模型,本文以样条插值和线性插值为基础,对插值前后数据进行相关性分析。
1 相关性分析理论基础
本文以一组单通道高温SQUID 所测得6×6 的心脏磁场离散数据进行研究。测得数据共有36组,每组数据包含有753个点。对插值前后的数据在相关性理论基础上进行时域相关性分析[6-11]。
1.1 心磁相关序列
心磁相关序列是在计算一组心磁周期与下一组心磁周期之间相关系数的基础上构建而成的。为保证实验的认可度,从实测的36组心磁数据中随机抽取出2组数据记为A和B, 2组心磁周期间的相关系数计算公式为:
(1)
(2)

1.2 秩和检验
为了更加清晰地表征插值前后数据系统有无显著性差别,必须对插值前后的数据系统进行秩和检验。从实测36组心磁数据和插值后心磁数据中各随机抽取出一组数据组成X和Y2个样本,其分布函数各为F(x)和G(x)量为n的样本X1,X2,…,Xn和Y1,Y2,…,Yn,且2个样本独立,欲检验假设H0:F(x)=G(x)。
2个心磁样本秩和检验方法的步骤如下:
(1) 把2个心磁样本观测值x1,x2,…,xn和y1,y2,…,yn混合,再按其值大小排列,得到m+n个秩,把xi的秩记为Ri,yj的秩记为Sj,得到秩代替原来的样本,最后得到2个样本的秩为:
(3)

秩和为离散型随机变量,取值范围为:
用秩和T统计量去检验原假设H0:F(x)=G(x),即2组心磁数据没有显著性差别。因为当H0:F(x)=G(x)为真时,2个心磁样本X和Y实际上是一个数据系统,因此,第1个心磁样本的秩一定随机均匀地分散在开头到各个自然数中而不会过度集中在较小或较大的数中,可知秩和T不会太靠近取值范围两端的值。若太靠近取值范围,则两端的秩就认为出现了小概率事件,即
(4)
2 仿真结果及分析
2.1 时域相关性分析结果
采用三次样条插值法和线性插值法,在2个实测数据点间再计算出20数据点插入,可得原始数据和2种不同插值法计算后数据间的方差、相关系数和峰度图,如图1、图2所示。

图1 线性插值与原始数据相关系数、方差、峰度比较

图2 样条插值与原始数据相关系数、方差、峰度比较
由图1、图2可知,2种插值之后的数据特性与原始数据保持了一致性和完整性;通过对相关系数的比较可以得出插值前后心磁数据间的形态差异很小。在医学信息诊断应用上为进一步研究提供理论基础。
将线性插值数据与原始心磁数据和样条插值数据与原始心磁数据分别从中随机取出6组进行秩和检验,结果见表1所列。表1中,P为插值前后样本总体是否相同的显著性概率,P越是接近1表明插值后的数据与原数据相同的概率越大;P接近0则可以认为对原假设质疑。H为检验结果,当H=0时表示X和Y总体差别不显著,当H=1时表示X和Y总体差别显著。本次实验默认的显著水平为0.05。

表1 心磁数据插值前后秩和检验结果
从表1可以看出:① 插值前后两样本总体均值相等的概率,非常接近于1;②H=0也可以说明接受原假设。即从2个方面都可认为插值前后2个心磁周期的样本数据无明显差别。
2.2 频域相关性分析结果
心磁数据中包含丰富的频谱信息,本文利用快速傅里叶变换(fast Fourier transform,FFT)方法,对插值前后心磁信号通过非递归型(finite impulse responrse,FIR)高通、低通滤波器滤波后在频域范围内进行幅频、相频以及频谱图对比分析。
采用三次样条插值法和线性插值法,在原始心磁数据2个相隔实测数据点间计算新的200数据点插入,最后绘制出原始数据和2种不同插值法之后V1导联的频谱,如图3~图6所示。

图3 原始数据频谱、相频分析结果
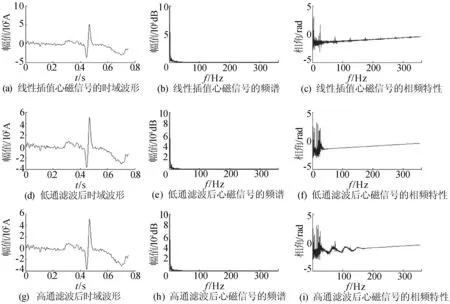
图4 线性插值频谱、相频分析结果

图6 插值前后幅频比较结果
由图3可知,在没有滤波的情况下,原始数据的相频图杂乱无章,经过FIR低通滤波器的处理能滤去高频部分的干扰,但是由于人体电磁信号通常都是微弱的低频信号,因而原始数据经过高通滤波之后无法滤去低频干扰。对比图3、图4与图5可以得出,无论何种插值方法之后的数据都被滤去了50 Hz的工频干扰;插值之后的数据相频图相对原始数据相频图来说,更加平滑且有低通滤波器的功效。对比图4和图5,可以看出样条插值比线性插值在高频滤波部分变得更为出色,并且将低频部分变得更加平滑;此外样条插值比线性插值之后的数据相频图更加光滑,抖动更小,有利于进一步绘制心磁图等。由图6可以看出,插值之后并没有影响数据的频谱完整性。
3 结 论
实测心磁信号是离散的、有限的、关于时间的数据序列,将心磁数据通过插值合理地在实测点间插入数据,使其包含足够的数据量来进行心磁图计算,提高精度,从而更有利于辅助医生诊断,这样能解决实测数据困难且有限的缺点,但必须不能损害原始心磁数据的完整性。本文采用线性插值和三次样条插值分别在实测原始数据高、低频滤波中使用,研究了36组实测的心磁数据与2种不同插值方法之后系统的相关性分析,证实了插值前后的心磁数据形态没有差别,随后引入秩和检验判断了插值前后的系统没有显著性差别。本文对实测数据进行了丰富,从而有助于填充图像变换时像素之间的空隙,但未考虑到数据的测量精度,将在以后的研究中进行改善。
[1] 陈波,刘冬梅,陈薇.基于插值的准周期电生理信号样本构建的研究[J].电子测量与仪器学报,2013,27(12):1127-1133.
[2] 王倩,马平,华宁,等.基于心磁信号的心脏电流偶极子阵列成像及相关性质的研究[J].物理学报,2010,59(4):2882-2888.
[3] 唐烁,杨明娟.二元牛顿关联连分式插值的矩阵算法[J]. 合肥工业大学学报(自然科学版),2010,33(8):1260-1263.
[4] 孔维华,林京. 医学图像的多方向加权层间插值算法[J]. 合肥工业大学学报(自然科学版),2010,33(9):1438-1440.
[5] 陈浩,华灯鑫,张毅坤,等.基于三次样条函数的激光雷达数据可视化插值法[J].仪器仪表学报,2013,34(4):831-837.
[6] 任崇玉,张妍.同步脉搏心电信号的混沌特性分析[J].兰州理工大学学报,2011,37(5):83-87.
[7] 孙静,黄丹飞,乔洪勇.脑梗塞时心电信号和脑电信号的相关性分析[J].长春理工大学学报(自然科学版),2014,37(1):156-159.
[8] 刘蓉,李春月,王永轩,等.基于序贯似然比检验的运动想象脑电信号分类方法研究[J].大连理工大学学报,2013,53(6):898-902.
[9] 蔡超峰,张勇,郭舒婷,等.思维脑电信号的关联维数分析[J]. 河南科技大学学报(自然科学版),2012,33(1):37-40.
[10] 刘澄玉,赵莉娜,刘常春.生理信号时间序列周期性和平稳性对近似熵和样本熵算法的影响分析[J]. 北京生物医学工程,2012,31(2):154-158,163.
[11] 谌玉红,郑捷文,李晨明,等.不同负荷模拟行走时的生理、生物力学信号分析[J].北京生物医学工程,2014,33(6):603-608.
(责任编辑 张 镅)
Study of MCG signal correlation based on interpolation process
CHEN Hao, CHEN Bo, LI Hua, CHU Zhaobi, KONG Yan
(School of Electric Engineering and Automation, Hefei University of Technology, Hefei 230009, China)
Interpolation is an effective method to enrich discrete data. In this paper, on the basis of the construction of magnetocardiography(MCG) correlation sequence, the correlation analysis of the discrete MCG data before and after interpolation is conducted, and the statistical rank sum test is introduced to determine whether there is a significant difference between the interpolated data and the primitive one. Finally, the interpolated and primitive data is analyzed in the frequency domain. Based on the results of the correlation and statistical rank sum test analyses, it is pointed out that there is a specific relationship between the data systems before and after interpolation and there is no significant difference between the interpolated data and the primitive one. The correlation coefficient, variance, kurtosis and amplitude-frequency waveform keep consistent after interpolation. Therefore, the interpolation is an effective method to enrich MCG medical data.
correlation; interpolation; magnetocardiography(MCG) data
2015-08-20;
2015-10-09
国家自然科学基金青年科学基金资助项目(11105037)
陈 浩(1992-),男,安徽六安人,合肥工业大学硕士生; 储昭碧(1970-),男,安徽岳西人,博士,合肥工业大学教授,硕士生导师.
10.3969/j.issn.1003-5060.2017.02.012
TP391.41
A
1003-5060(2017)02-0200-05

