考虑润滑因素的两圆柱体接触承载能力的分形模型研究
徐 帆, 陈 奇, 马运波, 张 振
(合肥工业大学 机械工程学院,安徽 合肥 230009)
考虑润滑因素的两圆柱体接触承载能力的分形模型研究
徐 帆, 陈 奇, 马运波, 张 振
(合肥工业大学 机械工程学院,安徽 合肥 230009)
为了研究润滑对两圆柱体结合面接触承载能力的影响,文章引入弹性流体动压润滑理论,在分形理论M-B接触模型的基础上,结合弹性流体动压润滑机理,利用雷诺方程、Grubin积分法以及Hamrack关于最小油膜厚度的修正公式,推导了考虑弹性流体动压润滑状态下的两圆柱体结合面分形接触模型。通过Matlab仿真发现,弹性流体动压润滑能明显地减小圆柱体结合面接触应力,且随着润滑油膜厚度的增加,接触应力上升;随着粗糙度幅值减小、分形维数增加、啮合曲率半径变大,两圆柱体间的接触应力减小,且外啮合比内啮合时的接触应力大。该文将润滑因素引入圆柱体分形接触模型中,为后续进行真实工况下的齿轮接触分析奠定了一定的理论基础。
润滑;圆柱体;接触承载能力;分形理论
齿轮接触承载能力的分析至关重要,目前常用的方法有Hertz 弹性接触理论[1]和有限元理论[2],但该理论只适用于光滑表面且无润滑的静态接触。后来有学者将分形理论应用于接触力学特性的分析,其中以Majumdar-Bhushan 创建的M-B 模型[3-4]为典型代表;本研究团队在该模型的基础上,建立了任意两曲面[5]、两球面[6]以及两圆柱面[7-8]的分形接触模型,并成功应用于齿轮的承载能力分析[8]。然而上述模型分析未考虑润滑因素对接触承载能力的影响。
对于齿轮和轴承等点接触或线接触的接触情况,绝大多数是工作在部分膜弹流润滑状态下,弹流油膜的厚度通常在0.5~5.0 μm之间,而机加工圆柱体的表面轮廓跳动在0~10.0 μm之间,故齿面因切削形成的粗糙度和它同一个数量级,接触表面依靠润滑油膜与峰点接触共同承载。油膜厚度、接触性质、接触表面的微观形貌以及表面纹理方向等均对润滑产生影响。文献[9]提出的“平均流动模型”建立了三维粗糙表面平均Reynolds方程,通过压力流量因子和剪切流量因子的计算,定量揭示了膜厚比与表面纹理的方向性对润滑性能的影响规律;文献[10]针对“平均流动模型”计算的复杂性,引入了接触因子的概念并建立了部分膜润滑方程;文献[11]根据椭圆弹塑性接触模型,计算了粗糙峰微接触对润滑的影响。但是,上述关于润滑条件的表面承载能力分析没有考虑表面形貌的微观因素对接触承载的影响。
本文以齿轮啮合模型的简化圆柱体啮合模型为研究对象,结合分形理论,在圆柱体分形接触模型和弹性流体动压润滑研究的基础上,引入润滑因素对齿轮接触应力的影响,建立考虑润滑因素的圆柱体结合面分形接触模型;通过对模型中各参数变化对接触性能影响的预测分析,并利用Matlab进行模型仿真,得出不同参数与接触承载能力之间的影响趋势与规律,给出对比和分析结果,为圆柱体接触面的承载分析及其相关产品的接触应力计算提供了一定的理论参考。
1 理论基础
1.1 微凸体变形分析
假设粗糙表面间的接触为粗糙表面与理想刚性平滑表面之间的接触,其模型如图1所示。
在弹性流体动压润滑方式下,设油膜的厚度为h(图1a),则微凸体油膜之外的高度值为:
(1)
其中,Δh为油膜厚度跳动差量;z(x)max为形貌轮廓跳动量的最大值。由参考文献[12]可知,粗糙表面微观形貌满足W-M函数,则变形之前的微凸体轮廓跳动量(图1b)可以表示为:
(2)
其中,z(x)为微凸体轮廓跳动量;x为轮廓位移坐标;D为表面轮廓分形维数,它定量地度量表面轮廓在所有尺度上的不规则和复杂程度;G为反映z(x)大小的特征尺度系数;l为轮廓线上的接触长度。

图1 M-B分形接触模型
根据微凸体的弹塑性变形研究,微凸体的顶端变形量δ为:
(3)
其中,a为变形之后的微凸体接触面积。
1.2 弹性流体动压润滑油膜的受力分析
弹性流体动压润滑(elastic-hydrodynamic lubrication,EHL)在分析刚性柱体接触时,根据润滑油黏度是否变化将接触分析分为2类。
(1) 等黏度状态。等黏度情况主要利用雷诺方程和Martin公式进行问题分析。根据圆柱体接触状况,雷诺方程为:
(4)
最小油膜厚度h0可以由抛物线函数推出,即
(5)
将(5)式代入(4)式,积分求解可得线分布承载量wz的近似表达式为:
(6)
(2) 变黏度状态。变黏度情况主要利用Barus方程表征雷诺方程中的黏度η变化情况,得出分析结果。由Barus方程有:
(7)
同理,结合(4)式和(7)式,利用Grubin积分法对雷诺方程的积分求解和Hamrack对最小油膜厚度的修正公式,可得wz的近似表达式为:
(8)

2 分形接触应力分析
根据油膜跳动差量Δh与微凸体的顶端变形量δ之间的大小关系,将弹性流体动压润滑状态下的微凸体接触状况分为以下几种。
(1) Δh≤0时,润滑油膜承担全部接触载荷。此时h≥z(x)max,如图2所示,所有的微凸体均处于油膜之下,法向接触压力p首先接触油膜,油膜承担绝大部分的载荷,润滑状态趋近于理想的液体动压润滑,接触体基本不发生变形,此时分形理论已不再适用,故忽略此种情况。

图2 Δh≤0时的简化接触模型
(2) 0<Δh≤δc时,微凸体和润滑油膜共同承担接触载荷,其中δc为弹塑料性临界变形曲率。此时简化接触模型如图3所示。微凸体的顶端变形量达到h之后,润滑油膜和微凸体共同承担接触载荷,若忽略润滑油膜的厚度变化量,则微凸体顶端无法继续纵向变形形成大曲率接触点,因此微凸体处于塑性变形状态。

图3 0<Δh≤δc时的简化接触模型
根据(3)式,当δ=h时,润滑状态下的微凸体接触面积aR为:
(9)
设微凸体接触面积图形为圆形,则接触线长度为:
(10)
参照G-W模型和M-B分形接触模型[13],弹性变形下法向载荷与面积之间的公式为:
(11)
塑性变形下法向载荷与面积之间的公式为:
(12)
其中,σy为屈服强度;K为相关系数。结合(6)式和(8)式,对于单个微凸体,等黏度状态和变黏度状态的润滑油膜分担的接触载荷分别表示为:
(13)
(14)
处于塑性变形状态的微凸体,由(12)式有:
(15)
其中,aS为最小变形接触面积,一般取aS=0。
根据(13)式~(15)式,0<Δh≤δc时的结合面接触应力公式为:
(16)
其中,PR随润滑黏度的假设方式选取不同而变化,如(13)式和(14)式;aC为微凸体由弹性到塑性变化的临界面积。
(3)δc<Δh≤δl时,微凸体和润滑油膜共同承担接触载荷。此时简化的接触模型如图4所示,微凸体在法向接触载荷的作用下,曲率半径大于δc,微凸体发生弹性变形,若忽略润滑油膜的厚度变化量,微凸体顶端则无法继续纵向变形,因此由润滑油膜和微凸体共同承担接触载荷。

图4 δc<Δh≤δl时简化接触模型
结合(9)式~(15)式,此时aR>aC,该部分的微凸体处于弹性变形状态,微凸体和润滑油膜共同承担法向接触载荷,即
(17)
(4) Δh>δl时,微凸体承担全部接触压力。此时,润滑油膜厚度和接触结合面的微观形貌轮廓跳动量z(x)不属于同一个数量级,润滑作用接近于0,接触问题趋近于无润滑状态,法向接触应力全部由微凸体承担,在此不做详述。
3 分形接触模型
在“岛屿面积分布理论”的基础上[12],结合上述弹性流体动压润滑状态下的微凸体接触状态分析,接触面积超过aR的微凸体个数为:
(18)
对(18)式微分,则微凸体的面积分布为:
(19)
由文献[10]中构造的表面接触影响系数,直接修正接触面积分布函数,可得:
(20)
其中,xh=(1/R1)±(1/R2)(“+”为外啮合,“-”为内啮合),R1、R2分别为接触圆柱体的端面半径;圆柱体接触一般取C2=1/2。
总的实际接触面积为:
(21)
综合以上公式,弹性流体动压润滑状态下的圆柱体分形接触无量纲模型如下。
当最大接触点面积al>aC时,接触点发生弹塑性变形,考虑到数值计算中分形维数D的取值问题,将公式分为2种形式,即
(1) 当D=1.5时,有
(22)
(23)
(24)
(25)
(2) 当D≠1.5时,有
(26)
(27)
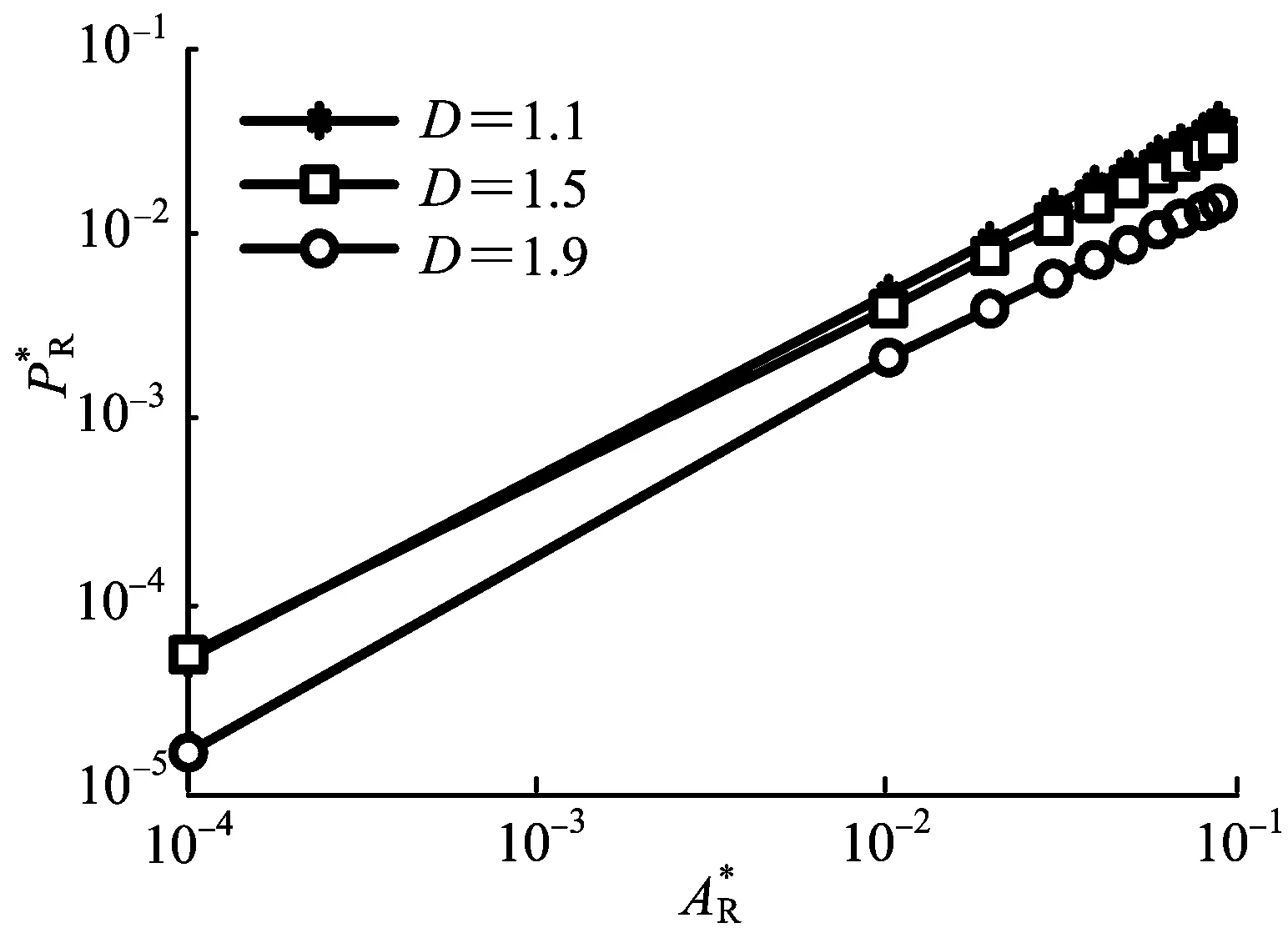
当al (28) (29) (30) 润滑油膜厚度与实际接触面积关系如图5所示。由图5可知,随着润滑油膜厚度h的增加,实际接触面积AR随之呈现非线性减小,结合(9)式和(21)式,在弹性流体动压润滑状态下油膜厚度增加,大曲率半径的微凸体也开始被油膜覆盖,实际粗糙结合面的微凸体接触面积减小。 图5 润滑油膜厚度与实际接触面积关系 润滑条件下圆柱体接触强度、分形接触强度以及圆柱体接触强度的模型对比如图6所示。将弹性流体动压润滑状态下的接触应力与M-B分形及圆柱体接触强度模型对比发现,图6a中的接触载荷随着真实接触面积的增大而增大,与图6b中模型变化趋势一致,说明润滑状态下的模型整体趋势是正确的;而在润滑条件下,本文假设润滑油膜厚度是不可形变的,从而接触微凸体只承担了一部分法向接触载荷,另一部分由润滑油膜承担,因此在图6a中,相同数量级的接触面积下,弹性流体动压润滑条件下的接触应力要稍小一些。 图6 3种接触强度的模型对比 等黏度和变黏度情况对比如图7所示。 图7 等黏度和变黏度情况对比 由图7可知,随着润滑油膜厚度的增加,变黏度情况下的油膜分担法向载荷远远大于等黏度情况下的,这种情况与格鲁宾分析法的结果相近;变黏度情况下,润滑油随着接触载荷的增加,黏度急剧增加,提供更大的承载能力。由此可见,本文所建立的等黏度模型与实际工况相差较大,在模型使用中,应该选用变黏度强度模型。 不同粗糙度幅值的接触强度如图8所示。由图8可知,随着粗糙度幅值的增加,相同的真实接触面积对应的法向接触载荷增加;在考虑润滑条件下相同分形维数时,随着粗糙度幅值的增加,弹性变形和塑性变形的临界变形量减小,同样厚度的润滑油膜所分担的法向接触载荷也随之减小,所以微凸体法向接触载荷增加,承载能力下降。 图8 不同粗糙度幅值的接触强度 不同分形维数时的接触强度如图9所示。由图9可知,在相同的法向载荷条件下,随着分形维数的增加,真实接触面积也增加,使得弹性流体动压润滑条件下润滑油膜承担的法向载荷减小,表面接触承载能力也变小。弹性流体动压润滑条件下的微凸体承担的法向载荷在D∈[1.1,1.5]时几乎保持不变,在D∈[1.5,1.9]时逐渐减小。 图9 不同分形维数时的接触强度 由(24)式和(25)式可知,无论是等黏度还是变黏度情况下,随着啮合曲率半径的增加,润滑油膜所承担的法向载荷增加。 不同曲率半径时的接触强度如图10所示。由图10可以看出,与不考虑润滑的圆柱体分形接触强度模型相比,随着啮合曲率半径的增加,微凸体承担的法向载荷都呈现减小趋势,且外接触情况比内接触情况下的接触载荷大,这与理论模型和实际情况相一致。但是受润滑油膜分压的影响,弹性流体动压润滑时,圆柱体间的啮合曲率对微凸体接触承载能力的影响更为明显。 图10 不同曲率半径时的接触强度 本文在圆柱体结合面分形接触承载能力研究的基础上,结合弹性流体动压润滑机理,利用雷诺方程、Grubin对雷诺方程的积分法以及Hamrack关于最小油膜厚度的修正公式,建立了润滑状态下的圆柱体结合面分形接触模型,并在Matlab中进行了仿真分析。 (1) 与干摩擦相比,弹性流体动压润滑条件下的接触应力要稍小一些,但随着润滑油膜厚度的增加,两微凸体间的实际接触面积随之呈现非线性减小,接触应力上升。 (2) 在考虑润滑条件的情况下,相同的分形维数时,随着粗糙度幅值的增加,弹性变形和塑性变形的临界变形量减小,接触应力增加,承载能力下降。 (3) 随着分形维数的增加,弹性流体动压润滑条件下润滑油膜承担的法向载荷减小,表面接触承载应力也变小,承载能力增加;弹性流体动压润滑条件下的微凸体承担的法向载荷在D∈[1.1,1.5]时几乎保持不变,在D∈[1.5,1.9]时逐渐减小。 (4) 与不考虑润滑的圆柱体分形接触强度模型相比,随着啮合曲率半径的增加,微凸体承担的法向载荷都呈现减小趋势,且外接触情况比内接触情况下的接触载荷大;弹性流体动压润滑时,圆柱体间的啮合曲率对微凸体接触承载能力的影响更为明显。 [1] JOHNSON K L.Contact mechanics[M].Cambridge,Eng.:Cambridge University Press,1987. [2] 张允真,曹富新.弹性力学及其有限元法[M].北京:中国铁道出版社,1983. [3] 张汝清,詹先义.非线性有限元分析[M].重庆:重庆大学出版社,1990. [4] BHUSHAN B,MAJUMDAR A.Elastic-plastic contact model for bifractal surfaces[J].Wear,1992,153(1):53-64. [5] 陈奇,黄康,张彦,等.两任意轮廓弹性体接触应力计算的分形模型研究[J].机械强度,2012,34(4):557-561. [6] ZHAO H,CHEN Q,HUANG K.Analysis of two ball’s surface contact stress based on fractal theory[J].Materials Science Forum,2011,675/676/677:619-627. [7] 黄康,赵韩,陈奇.两圆柱体表面接触承载能力的分形模型研究[J].摩擦学学报,2008,28(6):529-533. [8] 陈奇,赵韩,黄康,等.分形理论在齿轮接触应力分析中的应用研究[J].中国机械工程,2010,21(9):1014-1017,1057. [9] PATIR N,CHENG H S.An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication[J].Journal of Tribology,1978,100(1):12-17. [10] MILLS R S,AVAN E,DWYER-JOYCE R S.Piezoelectric sensors to monitor lubricant film thickness at piston-cylinder contacts in a fired engine [J].Proceedings of the Institution of Mechanical Engineers,Part J: Journal of Engineering Tribology,2013,227(2):100-111. [11] 汪家道,陈大融,孔宪梅.粗糙峰微接触及其对润滑的影响 [J].摩擦学学报,1999,19(4): 362-367. [12] 葛世荣,朱华.摩擦学的分形[M].北京:机械工业出版社,2005. [13] MAJUMDAR A,BHUSHAN B.Fractal model of elastic-plastic contact between rough surfaces[J].Journal of Tribology,1991,113(1):1-11. [14] XIAO L,ROSEN B G,AMINI N,et al.A study on the effect of surface topography on rough friction in roller contact[J].Wear,2003,254(11):1162-1169. (责任编辑 胡亚敏) Research on fractal contact model for contact carrying capacity of two cylinders’ surfaces considering lubrication factors XU Fan, CHEN Qi, MA Yunbo, ZHANG Zhen (School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China) In order to study the influence of lubrication on the contact strength between two cylinders, the fractal contact strength model considering the elasto-hydrodynamic lubrication was derived by Reynolds equation, Grubin integral method and Hamrack correction formula of minimum oil film thickness based on the elasto-hydrodynamic lubrication theory, M-B fractal contact model and elasto-hydrodynamic lubrication mechanism. The numerical results in Matlab show that the contact stress between two cylinder surfaces is obviously reduced with the elasto-hydrodynamic lubrication; the contact stress increases with the growth of the thickness of lube film; the contact stress between the two cylinders reduces as the roughness amplitude decreases and the fractal dimension and meshing radius of curvature rises; the contact stress with the external meshing is larger than that with internal meshing. The introduction of lubrication factor into the fractal contact model for cylinders can lay a theoretical foundation for subsequent analysis of gear contact under the real working conditions. lubrication; cylinder; contact carrying capacity; fractal theory 2015-12-14; 2016-03-31 国家自然科学基金资助项目(51305116) 徐 帆(1993-),男,江苏常州人,合肥工业大学硕士生; 陈 奇(1979-),男,安徽合肥人,博士,合肥工业大学副教授,硕士生导师. 10.3969/j.issn.1003-5060.2017.02.006 TH114 A 1003-5060(2017)02-0169-06
4 Matlab仿真对比分析






5 结 论

