冲激噪声下相干信源的求根MUSIC算法
陈栋 杨保海 丁文斌

摘 要: 由于在冲激噪声背景下,MUSIC算法对信源波达方向估计将失去韧性,且无法解相干,运算量较大,为此对前后向平滑算法和修正的MUSIC算法进行了改进,提出相干信源波达方向估计新算法。简要分析了线阵模型以及共变,将阵列输出矩阵从二阶原点矩扩展到低阶矩,通过分析共变矩阵,得到基于共变矩阵的空间谱,再将谱峰搜索转变为多项式求根,最后可得相干信源波达方向估计。通过仿真,在冲激噪声或高斯噪声下,改进算法可以对相干信源的波达方向进行正确估计。算法性能分析表明改进算法具有良好的稳健性。
关键词: 冲激噪声; MUSIC算法; 相干信源; 波达方向; 共变矩阵; 求根
中图分类号: TN911.1?34 文献标识码: A 文章编号: 1004?373X(2017)05?0001?04
Abstract: Under the background of impulse noise, the MUSIC algorithm will loss the tenacity for the DOA (direction of arrival) estimation of the signal source, cant perform the decorrelation, and has heavy computation, therefore the forward?backward smoothing algorithm and modified MUSIC algorithm are improved to propose a new algorithm for DOA estimation of the signal source. The linear array model and co?variation are analyzed briefly. The output matrix of the array is extended from the 2?order origin moment to low?order moment. The spatial spectrum based on co?variation matrix is obtained by analyzing the co?variation matrix, and then the spectral peak searching is transformed into the polynomial rooting to estimate the DOA of the coherent signal source. The simulation results show that the algorithm can correctly estimate the DOA of the coherent signal source under the background of impulse noise or Gaussian noise. The analysis result of the algorithm performance shows that the algorithm has good robustness.
Keywords: impulse noise; MUSIC algorithm; coherent signal source; DOA; co?variation matrix; rooting
0 引 言
波达方向估计在雷达、声纳、通信等领域有广泛应用,MUSIC算法是波达方向估计的经典算法,但它是基于二阶矩,仅能够处理非相干信号,且运算量较大。实际环境中,往往存在冲激噪声,如大气噪声、海杂波噪声、人为噪声等,这类噪声具有尖峰及厚拖尾,不存在有限的二阶矩[1?5],同时空间存在大量相干信号,所以MUSIC算法性能将显著退化且不易实时处理。本文分析了在冲激噪声下基于共变的求根前后向平滑算法和求根修正的MUSIC算法。
1 信号模型及噪声模型
1.1 信号模型
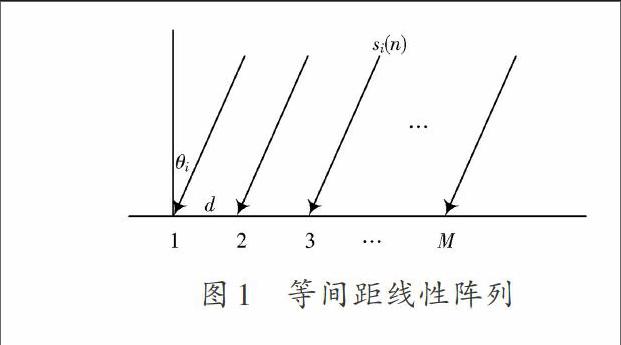
如图1所示,设有[P]个远场、窄带、平稳信号源。[M]个全向无差异阵元等间距线性排列,阵元间距[d。][θi]表示第[i]个信号[si(n)]到达各阵元入射线与阵列法线方向的夹角,即波达方向。
1.2 噪声模型
冲激噪声可用[SαS]分布进行描述[1?5],它有4个参数:特征参数[α]表示分布的冲激及拖尾程度,越小冲激越大且拖尾越重;尺度参数[σ]表示分布的离散程度,相当于二阶矩的方差;偏斜参数[β]表示分布相对于其中心点左右分布的对称程度,等于0;位置参数[μ]表示分布的位置,相当于二阶矩的均值。
2 改進的解相干MUSIC算法
空间平滑算法是目前较为有效的解相干算法,主要有前后向平滑算法[11]和MMUSIC算法[12]。通过将阵列分成若干个子阵, 取各子阵输出相关矩阵的算术平均值来解决秩亏损。在冲激噪声背景下,[Rxx]无法收敛,但共变矩阵[Γxx]收敛,可用[Γxx]代替[Rxx。]
2.1 改进的前后向平滑算法
如图2所示,阵列阵元数为[M,]每个子阵阵元数为[K,]子阵数目为[L。]
3 改进的解相干求根MUSIC算法
算法进行方向估计是通过对空间谱搜索实现的,搜索步进越小,估计精度越高,从而实现高分辨率波达方向估计。然而,对空间谱的搜索会导致算法运算量较大,难以实现实时估计。为了降低运算量,可利用求根算法[13]将谱峰搜索转变为对多项式的求解。
4 计算机仿真及性能分析
4.1 计算机仿真
仿真条件:两相干信源入射角度为10°和60°;背景为特征参数[α=1.4、]尺度参数[σ=1、]偏斜参数[β=0、]位置参数[μ=0]的冲激噪声;信噪比均为5 dB;角度搜索范围为[-90°~90°,]搜索步进为0.1°;阵元间距为中心频率对于波长的一半。谱峰搜索如图3所示,改进的求根算法结果标注于谱峰旁。

