从“无限”走向“极限”———浅谈小学教学中“极限”思想的渗透之路

沈华斌

极限是指用以描述变量在一定的变化过程中的终极状态的概念。在小学数学的实际教学中，有些教师对极限思想方法的理解及应用还有所忽视，那么极限的思想方法其思想内涵又是什么，与“无限”有着怎样的联系，又如何渗透于小学数学教学之中，学生才能感悟其中的极限思想？本文将针对以上问题提出自己的观点。

一、从“无限”走向“极限”，培养学生无限观念

由于小学生受年龄特点的限制，他们对具体的、数量有限的事物容易理解，对抽象的、数量无限的事物难于把握。所以要理解“极限”的内涵，可以从“无限”入手，让小学生首先理解小学数学中的“无限”。

1.图形无限延伸。

小学几何概念中有许多概念是具有无限性的，如直线、射线、角的边、平行线的长度等等，它们都是可以无限延伸的，但是这些概念在现实生活中并不是真实存在的（现实生活中找不到一条能无限延伸的线），它们只是存在于人脑的想象之中，是人脑抽象的结果，而这种想象又是进一步学习数学的必不可少的基础能力。

2.数量无限多。

现行人教版小学教材中有许多知识点会涉及到数量无限多的情况。在“自然数”、“奇数”、“偶数”、“小数”这些概念教学时，教师可让学生体会自然数是数不完的；奇数、偶数的个数有无限多个；小数没有最小的数；通过一点可以画无数条直线等等。

比如四年级下册求0.5和0.6之间有几个小数，答案是无数个，写不完也数不完，让学生体会这样的小数是无穷无尽的。在五年级上册循环小数这一部分内容中，1÷6=0.1666……商是一个循环小数，它的小数点后面的数字是写不完的。通过这些方面让学生初步体会“无限”思想。

以上两点是从不同方面体现了“无限”的观念，虽然并不是真正意义上的“极限”，但是，培养学生的无限观念是初步形成极限思想的基础，是学生必经的一个阶段。

二、从“逼近”走向“极限”，积累极限感性认识

由于小学生的生活经验、数学知识还比较贫乏，他们只能通过一些具体的事例，逐渐感悟到什么是“无限地逼近”，为将来学习“收敛”这个数学中的概念积累一些感性的认识。因此，逐步理解“逼近”是形成极限思想的另一个重要方面。

例如特级教师张齐华在教学《圆的认识》的片断：深究圆与正多边形。

教师在让学生理解了圆之所以美，是因为在同一个圆里，半径处处相等，明白这一道理之后，课件出示正三角形，从中心出发，连接三个顶点，三条长度相等。再出示正四边形、正六边形、正八边形，最后是正三十二边形，正一百边形，然后让学生想象，如果是正一千边形、正一万边形，正一亿边形，直至无穷无尽，它就是——圆（学生答）。整个过程其实就是一个正多边形不断地逼近一个圆的过程，先通过课件实物引导，再想象无穷无尽多边形即是一个圆。张老师不断地引导学生理解随着边的无限增多，正多边形逐渐成为一个圆。

通过课件的不断演示，从正三角形不断地向圆“逼近”，在外形上越来越接近一个圆，直至真的成为一个圆，是一个不断的“逼近”过程。让学生在观看课件的同时，逐步理解正多边形随着边数的增多逐渐“无限地逼近”一个圆，在具体的情境中理解“无限地逼近”是一个怎样的概念。

三、从“感悟”走向“理解”，实践极限渗透教学

受年龄特征的制约，小学生可能对极限思想不会有深刻的理解，但这并不等于我们在小学数学教学中可以淡化对极限思想的渗透，相反我们应该抓住一切可以利用的契机加以渗透，为他们将来学习极限理论，掌握极限思想，提高抽象思维奠定基础。

1.概念教学渗透。

如此教学不但能激发学生学习数学的兴趣，而且对于发展学生智力，培养学生良好的思维能力是十分有益的，更重要的是渗透给学生极限的思想方法。

2.几何教学渗透。

片断二：人教版四年级上册《直线、射线和角》的教学，有多个渗透极限思想的点。一是直线的两端、射线的一端（没有端点）可以无限延伸，教学时，可以借助学生的想象，先让学生画一条直线，然后延长，再延长一直到不能画为止，这时可提问，还可以延伸吗，直至想象这条直线穿出教室、学校、我们所在的城市、地球的大气层……，教师让学生闭上眼睛，自己边说直线的路径，边让学生体会直线两端的无限延伸，从中体会其中的“极限”思想；二是经过一点可以画（）条直线，这里我们可以借助现代化工具制作多媒体课件，在让学生试画之后，出示课件，经过一个点的直线，1条、3条、10条、50条、上百条……直至变成近似于以这个点为中心的圆，而这个圆即是答案，个数是无限的，圆则是最终极限的结果。

通过有限想象无限，根据课件出示的数量变化趋势，想象它们的最终结果。既让学生掌握了直线的性质，又理解了无限逼近的极限思想。

3.练习教学渗透。

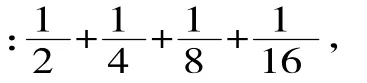
解决这题运用了极限和数形结合两种不同的思想方法，所以我们的练习设计不能仅仅着眼于一个问题的解决，而是关注学生在解决这个问题中领悟到其中的数学知识及思想方法，更关注在解决问题中充分锻炼学生的思维能力。

4.公式推导渗透。

片断四：《圆的面积》。在学生学过一些图形的面积计算公式后，研究圆的面积公式。先问学生有什么好的办法，再利用课件演示先把圆平均分成了2份，把两个半圆拼起来，结果还是一个圆。再多分几份试一试。课件又接着演示把一个圆分割为完全相同的小扇形，并试图拼成正方形。从平均分成4个、8个、到16个……然后问学生的发现，同学们通过分的过程，发现分的份数越多，拼成的图形就越接近长方形。

课件继续演示把圆平均分成32个、64个……，教师适时说“如果一直这样分下去，拼出的结果会怎样？学生发现拼成的图形就“真的”变成了长方形，因为边越来越“直”了。

这个过程中从“分的份数越来越多”到“这样一直分下去”的过程就是“无限”的过程，“图形就真的变成了长方形”就是收敛的结果。学生经历了从无限到极限的过程，感悟了极限思想的巨大价值。以上的推导过程，采用了“变曲为直”、“化圆为方”极限分割思路。