“双联”模式在“图形与几何”复习中的实践与策略研究

盛荣海

如何让复习课有新意？我们在教学中要尝试运用“联想+联系”的模式开展复习，努力让数学复习课既要做到“温故”，更要让学生“知新”，让学生在复习课上有新的收获。

一、让学生在“联想”中构建知识体系

联想是指由一个事物经验想起另一事物经验，或由想起的一个事物经验再想起另一事物经验。著名的中国科学院院士闵恩泽说过：“联想是创新的基础，创新催化神奇。”在复习课上教师可以提供有效的学习素材，让学生借助素材，在教师的引导下自己联想所学。

案例1：复习：图形与几何

师：看到这个课题你想到了什么？

生：我们今天要复习的是“图形与几何”的知识。

师：小学阶段我们已经学过哪些几何图形？

生1：长方形、正方形、平行四边形、三角形……

生2：长方体、正方体、圆柱、圆锥。

师：一节课里我们不可能复习所有的图形，这节课老师选择了两个代表：长方形和圆柱，想一想老师为什么会选择它俩？

生1：因为长方形是平面图形的代表，圆柱是立体图形的代表。

生2：因为圆柱可以通过长方形旋转变出来。

师：看到长方形你能想到哪些关于它的知识？

生1：长方形的周长＝（长+宽）×2。

生2：长方形的面积＝长×宽。

生3：长方形对边相等，有4个直角。

生4：长方形是轴对称图形，有两条对称轴。

……

师：我们可以把长方形的相关知识整理成一个表格。

图形　特征　周长　面积长方形4条边、对边相等；4个角，都是直角；是轴对称图形，有2条对称轴。C＝2（a+b） S=ab

师：看到圆柱你又能想到哪些关于它的知识呢？想一想，小组合作整理一下，可以用表格也可以用网络图。

有了前面长方形的整理经验，学生对圆柱相关知识的整理各有针对性，整理出了以下内容：

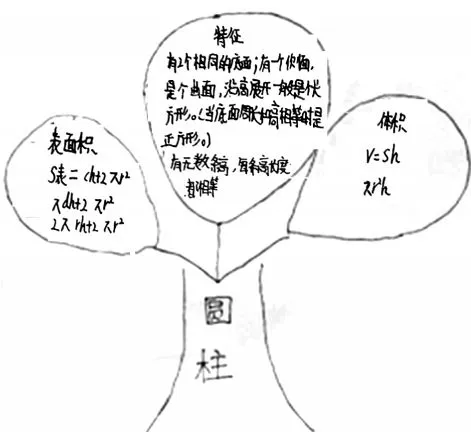
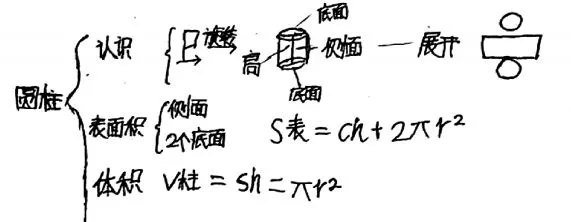
引入与整理环节，采用“素材+联想+分享”的复习方式是学生比较喜欢的一种学习方式，每个学生可以根据自己的认知水平，积极地参与到联想中去，身心都处于活跃的状态，学生对知识的回顾与整理的过程兴致盎然。更重要的是让学生体验到了一些复习的策略，如选择代表性的复习材料长方形和圆柱进行复习可以以点带面，提高效率；又如平面图形的复习可以参照长方形从特征、周长、面积这些维度进行复习整理；立体图形的复习可以从特征、表面积、体积这些维度复习整理，可以用表格也可以用网络图整理，当然也可以用自己喜欢的、有效的方式进行整理。在小学数学教学中联想作为一种极为重要的思维方式，有利于学生联想思维的训练与培养，促进学生创新意识的增强，提高学生的创新能力。利用教师提供的素材引导学生展开积极的联想，不仅可以唤起学生原有知识的回忆，而且还能根据自己的理解对知识进行分类整理，有效梳理，用自己独特的方式，把知识系统形象、简洁、合理地建构起来，使这些知识在学生头脑中竖成串、横成链、构成网、建立一个完整的知识网络体系。使学生加深对所学知识的理解，便于储存与运用。

二、让学生在“联系”中提升思维深度

在“图形与几何”的复习教学中，我们应该特别重视对各个对象之间关系的分析，从而帮助学生逐步建立起关于相应数学结构整体性认识，让学生逐步学会用“结构性观念”去认识和把握学习对象，特别是不同对象之间的联系与区别。

案例2：长方形与圆柱的联系

师：长方形是平面图形，圆柱是立体图形，那么它们有什么关系呢？看到长方形你能联想到圆柱吗？或者你能从圆柱里找到长方形吗？

师：先自己独立思考，然后把你的想法告诉你小组里的同学，你也可以听听组内同学的发现。

……

师：谁愿意与大家分享你们的发现？

生1：我们发现长方形旋转可以变成圆柱，像这样一张长方形纸绕一条边旋转一周就可以形成一个圆柱（边说边演示）。

师：看到生1的演示，大家能想象出那个圆柱吗？

呈现动画：

师：请同学们仔细观察，原来的长方形与圆柱有什么样的关系呢？长方形的长相当于圆柱的什么？宽呢？

生：长方形的长相当于圆柱的高，宽相当于圆柱的底面半径。

师：刚才我们是绕长旋转，如果我们绕宽旋转得到的圆柱又会是什么情况呢？

生：如果绕宽旋转得到的圆柱，那么宽相当于圆柱的高，长相当于圆柱的底面半径了。

生：我发现了绕谁旋转谁就是圆柱的高，另一条边就是圆柱的底面半径。

师：真棒！我们可以把我们的发现整理在下面的表格里。

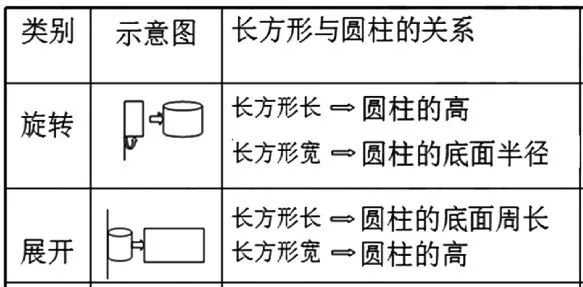
师：除了长方形旋转可以得到圆柱外，还有没有另外的关联了？

生2：我还知道圆柱侧面展开是一个长方形。像这个圆柱（由作业本卷成的圆柱）侧面展开（边操作边说）就是一个长方形。

师：你能找到这个长方形和圆柱的关系吗？

生：这个长方形的长是圆柱的底面周长，宽是圆柱的高。

师：真厉害，又发现一组。

生3：我们还发现把圆柱切开后的切面是一个长方形。

师：你能用这个模型说说你们的发现吗？

生：像这样（学生操作模型）把圆柱切成两半，这个切面是一个长方形，长方形的长是圆柱的高，宽是圆柱的底面直径。

师：你能具体说说你是怎样切的吗？

生：应该是沿直径垂直于底面切的。

师：那如果是这样平行于底面切，切面会是什么形状？

生：应该是一个圆。

师：这样切一刀，就圆柱的表面积来说，是增加了还是减少了，增加（减少）了多少？

生：切一刀，表面积增加两个切面面积。

师：真了不起，第三组了。

师：还有没有第四种情况了？

生：……

师：大家回忆一下，我们在推导圆柱体积公式时是怎样操作的，有长方形吗？

生：我想起来了，我们把圆柱切开转化成一个长方体，长方体上有长方形。

师：我这里有一个圆柱体（教具）你能来操作演示一下给大家看一下吗？

（学生操作把圆柱切拼成长方体）

师：请同学们关注这个长方体的这两个侧面，想想为什么？

生1：因为这两个侧面是长方形的。

生2：因为这两个长方形的面是切拼后多出来的面。

师：也就是说把圆柱切拼成长方体后，表面积是增加这样的两个长方形的侧面。那么这个长方形与圆柱又有什么关系呢？

生：长方形的长是圆柱的高，宽是圆柱的底面半径。

师：你们太棒了，我们发现了四种长方形与圆柱的关系，收获可真不小啊。

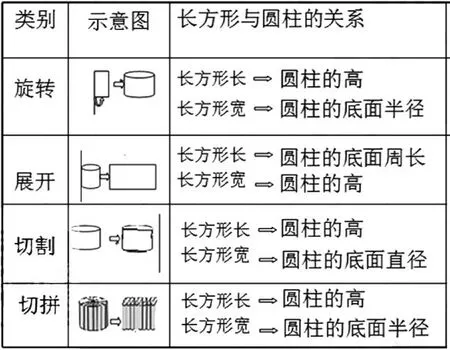
师：仔细观察这个表格，你又有什么发现？

生：我发现长方形的一条边总是圆柱的高，而另一条边可能是底面周长、直径或半径。

在数学教材中主要是按照逻辑顺序对各种数学概念和知识进行组织编排的，但是对数学概念和知识的理解更多的表现为能否对各个数学概念与知识之间建立更多更强的联系。因此在总复习的教学设计时，我们尝试突破常规的逻辑顺序的束缚，让学生从更为广泛的角度去认识和沟通各个概念和知识之间的联系，这成为了这节复习课的一个重要的目标。即通过复习促使学生将原来似乎互不相关的一些概念和知识联系起来，从而逐步形成整体性的知识结构。找“关系”这一环节中，教师把三年级学习的长方形和六年级学习的圆柱放在一起，这两个图形学生还真就没有把它们放在一起研究过，似乎它们并没有什么关联，而今天的课堂上学生通过操作演示，观察思考，讲解分享得到了这么多种长方形与圆柱的关系，学生感到很新鲜也很兴奋，也很有成就感。通过整理建构，让学生对长方形与圆柱关系有了更加清晰的认识和理解，为后面解决稍复杂的圆柱表面积的实际问题奠定了坚实的基础。因此在总复习的教学中我们应该注意沟通知识间的内在联系，从较为广泛的角度进行分析思考，这样才能准确地把握相关知识内容所蕴含的数学思想。当然也只能从数学思维的角度进行分析和思考，我们才能更好地把握各种数学知识内在的联系，所以我们要从整体上对复习内容进行设计，这对发展学生思维的广度、深度和完整度都是非常重要的。

二、让学生在“双联”并用中体验复习的乐趣

“联想”+“联系”的复习模式，让学生把分布在不同学段，不同时间内学习的零散知识沟通起来，找寻其中的逻辑顺序和关联，使所学知识条理化、系统化，形成完整的知识网络，达到以点带面的效果。

案例 3：“联想”+“联系”复习模式的运用。

师：今天我们运用“联想”+“联系”的模式复习了长方形和圆柱这两个几何图形。那么在“图形与几何”单元还有哪些知识也可以通过这种模式来复习。请同学们搜索一下，并根据它们之间的内在联系，尝试制作成表格或网络图。

1.学生根据长方形与圆柱关系的启发，整理出的三角形与圆锥的关系表。

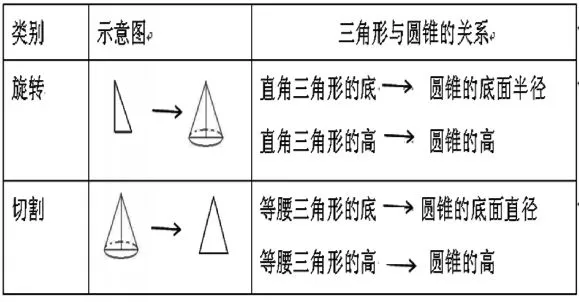
2.平面图形面积公式推导关系图。

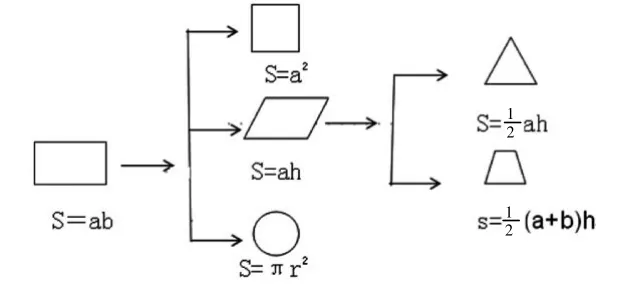
3.圆面积公式推导与圆柱体积公式推导关系。

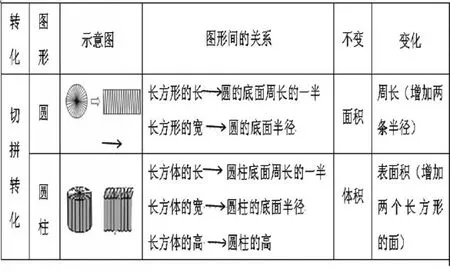
“联想”+“联系”的复习模式，让学生不仅建立知识的系统，而且要让学生认识系统内部结构中相关知识建立内在联系。这种认识既有横向的串联，又有纵向的并联。这种网络图的梳理过程，对学生来说是一次全新的且具有探究意义和挑战性的过程。