“生本教育”理念下的“学困生”转化策略

叶昊

【摘要】本文以《全等三角形的判定》教学为例，关注流动儿童生本课堂，探讨在初中数学“生本教育”中对于“学困生”会遇到的问题，通过对教学设计的改进达到提高教学效率的目的提出了建议。

【关键词】生本教育 《全等三角形判定》 思维定势

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2017）01A-0010-02

在城市迅速发展的今天，尽管城市教育资源得到了较大的改善，但仍存在教育资源不足的现象，因此，相当一部分流动儿童只能到办学条件相对较差的民办学校或农民工子弟学校就读。这些学校条件相对简陋、师资欠缺，一般难以保障教学质量，所以，流动儿童大多成为了学习能力中等偏下的“学困生”。倡导“生本教育”在重视优等生的培优教育的同时，对“学困生”的教育更应该予以重视。对此，本文以《全等三角形的判定》教学中“学困生”会遇到的问题为例进行分析，进一步提高“学困生”的课堂学习效率。

一、“学困生”在学习中常遇到的问题

《全等三角形的判定》是新人教版八年级上册的教学内容，本章内容第一节先介绍全等形以及全等三角形的性質、定义，第二节便开始通过找对应边、对应角相等来判定两个三角形全等。教学至此，一些问题就出现了：学习速度较快的班级只需要一节课甚至不到一节课的时间，就能完成从“探索最少需要多少个条件才能判定两个三角形全等”到“利用SSS来证明两个三角形全等”这些内容，此后就能展开练习，并在下一节课继续讲SAS、ASA及AAS等判定方法。而学习进度较慢的班级则会在第一个判定条件教学中用2-3节课的时间来讲解、练习、巩固，所以持续的时间会有2到3天，这样长时间停留在SSS的讲解中，在让学生加深记忆的同时，也让部分学生思维固化，特别是那些一直靠死记硬背学习的学生来说，“证明两个三角形全等”等于且只等于“找三组对应边用SSS证明”。这种情况在学习能力不是很强的“学困生”班级尤为突出。

二、全等三角形教学中让学生远离这一思维定势误区的对策

（一）不在第一个判定问题（SSS）上停留过长的时间

思维定势的形成需要一定的持续时间，如果能在一天之内接触到两个或两个以上的判定方法，就能让学生意识到全等三角形的判定方法其实有多种，从而打破思维定势。教师可以调整时间在有连堂课时上本节内容。但是短时间内大量知识的学习，需要学生有较强的接受能力、理解能力以及扎实的数学基础，所以这一方法只对部分学习能力较强的学生适用。

（二）改进教学过程，让SSS、SAS、ASA、AAS一起进入学生视野

本章第二节全等三角形判定的第一课时内容包含了“探索最少需要多少个条件才能判定两个三角形全等”“利用SSS来判定两个三角形全等”以及“判定全等三角形问题的证明格式”。这些内容对于学习能力不是很强的学生来说，要在一节课的时间内牢固掌握明显是力有未逮，导致教师不得不用更多的时间来讲解这部分内容。因此，教师在教学过程中可以因人而异，针对接受能力不足的“学困生”，适当地调整学习内容，把部分内容移到后面的章节中开展教学，以此来优化课程结构。教学设计如下：

1.回顾全等三角形的性质，学生集体回答三组对应边相等，三组对应角相等。

师：如果有这六个条件能否说明两个三角形是全等三角形呢？

生：可以。

师：条件数量是否可以减少？试着给出一个条件或者两个条件，画出一个三角形，然后观察是否与同桌画的全等？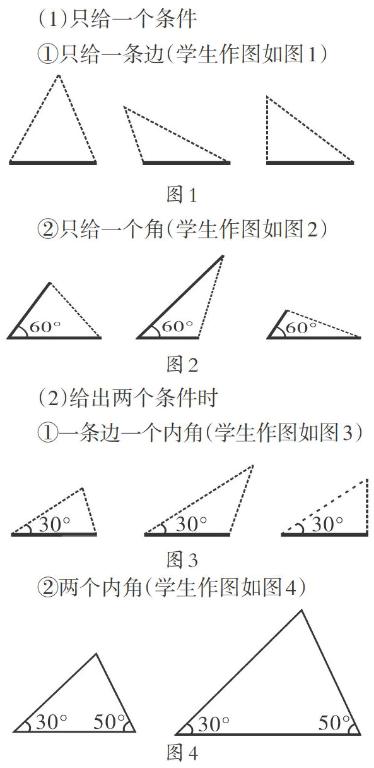

③两边（学生作图如图5）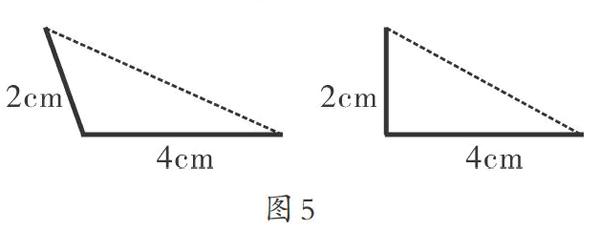

2.引出当有三个条件时，学生能画出部分三角形与其他学生画的三角形全等。

三条边（可以）、三个角（不可以）、两个角一条边（可以）、两条边一个角（部分可以、部分不可以）画法如下：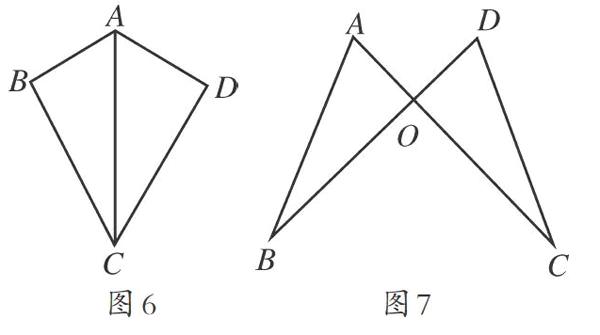

（1）画一个三角形，使它的三边长分别为4cm，5cm，7cm.

①画线段AB=4cm；

②分别以A、B为圆心，5cm、7cm长为半径作圆弧，交于点C；

③连接AB、AC.

（2）已知△ABC是任意一个三角形，画△DEF使∠D=∠A，DE=AB，DF=AC.

①画∠MDN=∠A；

②在射线DM，DN上分别取DE=AB，DF=AC；

③连接EF，得△DEF.

（3）已知△ABC是任意一个三角形，画△DEF使∠D=∠A，∠E=∠B，DE=AB.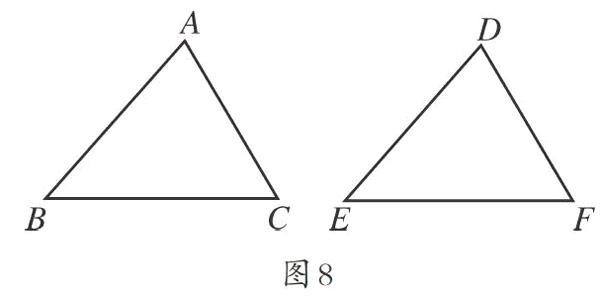

①画∠MDN=∠A；

②在射线DM上取DE=AB；

③画∠E=∠B；

④∠D与∠E边的交点为F，得△DEF.

总结：边决定三角形的大小，角决定三角形的形状，三角形要全等至少需要一条边相等。并得出全等三角形的4种判定方法SSS、SAS、AAS、ASA，且AAS与ASA其实是相同的，因为三角形内角和是180°，其中两个角相等那么第三个角也相等。

3.把对应这四种判定的四个简单的题目列出来，让学生通过观察找出自己认为在题目的图中全等的两个三角形，并加以证明。

练习（1）.如图6，AB=AD，BC=CD，求证：△ABC≌△ADC.

证明：在△ABC和△ADC中

△ABC≌△ADC（SSS）

练习（2）.如图7，在△AOB和△DOC中，AO=DO，BO=CO，求证：△AOB≌△DOC.

证明：在△AOB和△DOC中

AO=DO（已知）

∠AOB=∠DOC（对顶角相等）

BO=CO（已知）

∴△AOB≌△DOC（SAS）

練习（3）.如图8，∠A=∠D，∠B=∠E，AC=DF，求证：△ABC≌△DEF.

证明：在△ABC和△DEF中

∠A=∠D（已知）

∠B=∠E（已知）

AC=DF（已知）

∴△ABC≌△DEF（AAS）

练习（4）.如图9，∠A=∠D，∠B=∠E，AB=DE，求证：△ABC≌△DEF.

证明：在△ABC和△DEF中

∠A=∠D（已知）

AB=DE（已知）

∠B=∠E（已知）

∴△ABC≌△DEF（ASA）

4.让学生从题目中寻找与列出六组条件一致的条件，如果不够三个条件就再从题目的条件中寻找，看有没有能够推导出对应边、对应角相等的已知条件，例如中线、高、角平分线、平行等；最后如果还是不够就开始寻找图中有没有可以直接看出来的条件，例如公共边、公共角以及对顶角等，并总结归纳出缺条件时的解题思路：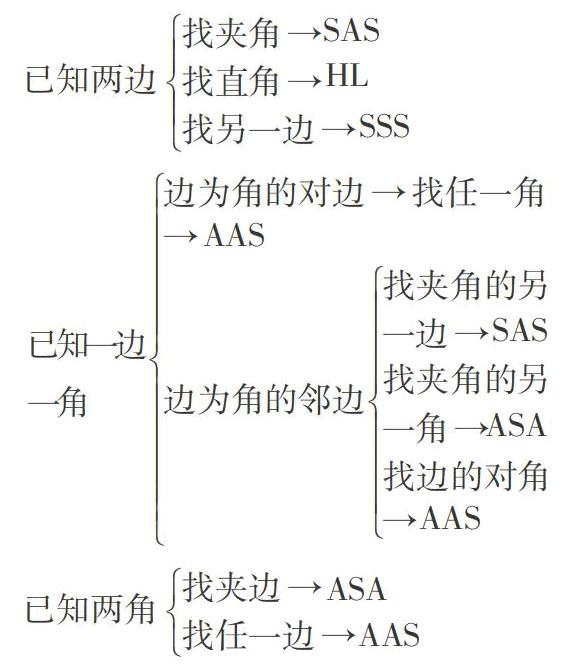

（将“判定全等三角形问题的证明格式”这部分内容押后。因为这部分内容的讲解及格式的练习会占用课堂教学的大部分时间，这是导致教学时间不足的一个重要原因。当把这部分内容押后以后教师就有充足的时间把四种判定方法一一向学生介绍）

5.通过学生的分组讨论及互相补充找出三个条件后，让学生对比四种判定所需的条件来找出此题应该用哪一种判定方法来证明。最后在学生能熟练掌握运用判定方法来证明问题后，才在后面的课堂教学中引导学生如何在选定方法后写出规范的证明过程。

由此可见，通过调节学习内容的先后顺序来让“学困生”能够同时接受四种判定方法来解决学生陷入思维定势的问题；通过几种判定方法的对比学习，能让学生快速有效地掌握知识，而不是一节课一种方法的传统的灌输式教学。

总之，在当今“生本教育”呼声日益强烈的环境下，教师不应墨守成规、照本宣科，而应结合学生的实际情况，改进教学方法和教学手段，而那些本就输在起跑线上的流动儿童更需要教师的重点关注，更需要教师为他们量身定制一套适合他们的教学方法，以更好地提高流动儿童的数学学习能力，提高课堂教学效果。

（责编 林 剑）