激光移除空间碎片过程的三维仿真与建模

张品亮，龚自正，杨武霖，陈 川

( 北京卫星环境工程研究所, 北京100094)

激光移除空间碎片过程的三维仿真与建模

张品亮，龚自正，杨武霖，陈 川

( 北京卫星环境工程研究所, 北京100094)

基于轨道力学和激光与物质相互作用理论建立激光移除空间碎片的三维变轨模型。该模型利用激光站/卫星与碎片位置和速度矢量作为初始数据，通过设定激光参数，实时计算和更新速度增量矢量，能够真实地反映碎片的移除过程。该模型包括地基和天基两种类型，根据激光作用临界条件与降轨效果计算碎片的降轨过程，能够实时输出碎片轨道信息，图形化输出使结果更加直观。考虑到速度增量分量对轨道倾角的影响，该模型增加了碎片逃逸情况的判断。最后，利用该模型计算了地基/天基系统移除多种空间碎片材料的过程和效果，发现钢材料碎片移除难度最大，而移除多层绝缘材料的效率最高。

激光烧蚀；空间碎片；变轨；三维仿真；数值模型

0 引 言

日益严峻的空间碎片环境，对航天器的安全运行造成严重威胁，减缓空间碎片的数量是空间技术发展面临的关键问题。近年来，以NASA和ESA为代表的航天组织对空间碎片移除技术进行了探索，提出了多种移除方法[1-5]。其中激光移除碎片技术具有独特的优势，是国际上一致认可的理想碎片移除方法，它具有操作简单、效率高、响应时间短和成本较低等优点。该技术的基本原理是：当高强度脉冲激光照射在碎片表面时，使表面材料等离子化产生高温气体，产生一系列类似于火箭反推的热物质反喷羽流，给碎片提供速度增量来降低近地点高度，使其在较短时间内落入大气层烧毁，达到移除空间碎片的目的。

激光移除碎片系统可分为地基[6]和天基[7]两种类型，它们各有优缺点。地基系统成本较低，维护方便，能量转化成本低，但是对碎片的监测时间受光照影响，并且容易受到大气干扰，效率较低。而天基系统可以实现全天监视，移除效率高，但维护困难，能源使用成本高。

从二十世纪末期开始，航天强国就已经开始激光移除碎片的技术论证。NASA将这个项目命名为ORION[8-9]。这项研究采用地基激光系统，主要针对高度在400～1100km的危险空间碎片。ESA也开展了激光移除空间碎片的计划CLEANSPACE[10]，该项目将建立一个从空间碎片环境监测、跟踪、识别到激光移除的系统框架。此外，中国学者也对空间碎片的监测[11]、定轨[12]和姿态跟踪导航[13]，以及激光与物质相互作用[14]、地基/天基驱动碎片变轨规律[14]等问题进行了研究。

无论地基还是天基，在激光移除碎片进程中，碎片的降轨是关键问题之一。目前已经建立了一些理论模型来计算碎片的变轨过程[14-15]，虽然这些模型可以定性地反映速度增量与降轨效果的关系;但是，它们以固定的速度增量作为初始数据[16]，而与激光物质相互作用分离开来，这样在计算中就忽略了碎片移动过程中速度增量的变化。此外，这些模型大部分为二维模型，假设激光与碎片轨道在同一平面上，而忽略了轨道倾角变化对速度增量的影响。因此，研究一种具有普适性的、应用更加灵活的三维模型对定量分析激光移除空间碎片的过程具有重要意义。

针对以上问题，本文基于轨道力学和激光与物质相互作用相关理论建立了三维变轨模型。该模型包括地基和天基两种类型，根据输入的激光和碎片相关参数，计算成功移除碎片所需的脉冲数量和作用过程，并且实现了图形化输出。

1 三维变轨模型

在三维空间的变轨问题中，根据地心赤道坐标系中碎片的初始位置和速度矢量，以及激光站的位置矢量，激光的波长、频率等参数，计算模拟空间碎片的降轨过程。

首先需要判断碎片是否具有移除条件，即：碎片的位置是否在激光的作用范围内。如果不在作用范围内，碎片按照脉冲时间间隔t开始移动，直到碎片进入激光作用范围内，开始计算脉冲激光与碎片的相互作用。依据相互作用机理，计算单次激光脉冲作用后碎片的状态矢量，得到变轨后碎片的轨道根数，判断激光脉冲作用后碎片轨道近地点高度是否降低，如果降低则使激光脉冲作用次数+1，更新变轨后碎片状态矢量；反则不作用，保持原轨道状态矢量。随后开始下一脉冲时间间隔t碎片状态的判断和计算，确定碎片的位置和速度矢量。以t为单位重复计算，直到近地点高度小于设定值(即移除成功)，或者碎片超出激光作用范围。对于后者，根据碎片的移动，重新判断碎片是否具有移除条件，开始二次或多次过顶/交会计算直到碎片被移除，或者逃逸出具备移除条件的轨道，无法继续移除。图1为模型的计算流程图。

1.1 轨道根数的确定

在地心赤道坐标系中，X轴指向春分点的方向，XY平面为地球的赤道平面，Z轴与地球的旋转轴一致，且指向北。单位矢量i、j和k满足右手定则。在给定时刻，空间碎片的初始状态向量速度v0和位置r0，在地心赤道坐标系中状态向量可表示为：

r0=x0i+y0j+z0k

(1)

v0=vx0i+vy0j+vz0k

(2)

在该点受到激光辐照后，获得速度增量

Δv=Δvxi+Δvyj+Δvzk

(3)

变轨后速度矢量和位置矢量分别为：

v=v0+Δv=(vx0+Δvx)i+

(vy0+Δvy)j+(vz0+Δvz)k

(4)

r=r0

(5)

根据二体运动方程和牛顿定律可以计算出变轨后的轨道根数[12]：比角动量的模h、轨道倾角i、升交点赤经Ω、偏心率e、近地点幅角ω和真近点角θ。

1.2 轨道与时间的函数

如果已知t0时刻的位置r0和速度v0，其模分别为r0和v0。可由拉格朗日系数f和g及其一阶导数，根据下述表达式求出任意时刻的位置r和速度v：

r=fr0+gv0

(6)

(7)

利用全局变量χ和斯达姆夫函数C(z)与S(z)所表示的拉格朗日系数如下：

(8)

(9)

(10)

(11)

其中长半轴的导数α为：

(12)

对于椭圆轨道，α>0。

如果已知Δt、r0、v0和α，可从全局开普勒方程中解出全局近点角χ，具体步骤如下：

计算χ0合理的初始估计值：

(13)

以χ0为初始数据进行迭代计算：

(14)

(15)

其中vr0为v0在r0方向上的投影,vr0=(r0·v0)/r0。

(16)

(17)

(18)

算出比值ηi=f(χi)/f′(χi)。如果|ηi|超出精度范围10-8，则按χi+1=χi-ηi重新选取χ估计值，计算式(14)、(15)直到|ηi|<10-8，则接受χi作为解。这样就可以根据式(6)、(8)、(9)得到Δt时刻的位置矢量r，根据式(7)、 (10) 、(11)得到Δt时刻的速度矢量v[17]。

1.3 判定激光作用条件

在地基移除系统中，由于受到大气的影响，理论上只有当天顶角在-45°～45°范围内才能使从地面发射的激光辐照在空间碎片上[18]。但是在计算中，向量夹角的范围在0～180°，需要根据碎片的坐标和象限来计算天顶角，特别是对于任意激光站位置和空间碎片轨道的情况，这无疑增加了计算的复杂程度。本文采用激光站地表切面的方法，对是否具备移除条件进行判断。

假设激光站坐标为 (x0,y0,z0), 碎片的位置矢量为(x1,y1,z1)，地球球面方程为：x2+y2+z2=63782，根据几何方法可确定激光站点在地球表面的切面方程：x0x+y0y+z0z=63782。

只有在碎片移动到激光站上方时(x1x0+y1y0+z1z0-63782>0)，才具有移除条件，此时向量夹角即为天顶角。这样就可对碎片的天顶角进行精确判断，而无需考虑碎片和激光站的象限问题。

在天基系统中，可根据碎片与激光卫星的距离来判断是否具有移除条件。本文认定300km为激光的作用范围。

当碎片进入作用范围后，需要判断是否适合进行激光辐照，如果作用后近地点高度降低则进行辐照，反则不辐照，碎片继续按原轨道移动，继续判断下一个脉冲的作用效果。

1.4 激光与碎片相互作用

激光辐照物体表面时，产生反喷冲量，使物体获得速度增量，冲量耦合系数反映了激光能量转化为物体冲量的能力。在确定速度增量时，激光与材料的冲量耦合系数是主要参数：

Cm=pτ/Φ=mΔv/E

(19)

其中，激光作用后靶的质量m=m0-μE；μ为激光烧蚀率(铝为80×10-9kg/J[18])；p为一个强度为I、脉宽τ的激光脉冲在靶上产生的烧蚀压；激光通量为Ф；E为靶上的激光能量。目前已经通过实验获得了多种材料的Cm值[19-20]。

为了在较大距离上将激光传输到靶上，需要数千焦的激光脉冲能量和大型发射镜来克服光的衍射：

(20)

ds=aM2λz/Deff

(21)

式中：ds为靶上光斑直径，M2为光束质量因子(≥1，1代表最好)，Deff为计算衍射时输出孔径D中的有效照射光直径，a为一个乘数因子，对于高斯光束a=4/π。对于一个从地基系统发出的高斯光束，修正后光束质量M2=2.0，Deff/D=0.9，a=1.7[19]。

如果需要将通量为Ф的激光辐照到距离为z的靶上，激光器需要输出WD2的激光[21]，

(22)

式中：W为激光脉冲能量，Teff为有效传输率。

研究表明[22]：不同形状的空间碎片在相同的激光脉冲下所获得的速度增量可能不同。对于激光辐照球体材料，所获得的冲量为垂直辐照平板材料的2/3[23]。在计算模型中，对激光辐照次数进行记录，每次辐照后碎片的质量变化都能够计算，从而获得精确的速度增量。

1.5 碎片逃逸

在三维轨道计算中，速度增量可能与碎片轨道不在同一个平面上，这样就会产生速度增量改变碎片的轨道倾角，当轨道倾角增加到一定程度时，碎片就逃逸出激光的作用范围，无法继续作用。在地基系统中，如果碎片沿当前轨道移动一周后仍然不具备激光辐照的条件，则认为碎片逃逸。在天基系统中，如果激光与碎片在100个轨道周期内不交会，则碎片逃逸。

2 计算实例

在地基系统中，本文采用波长为1.06μm的近红外激光，具体参数列于表1中，分别采用了1mm、1cm和10cm三种直径的球形铝碎片进行计算，初始轨道参数列于表1中。坠入大气层烧毁的判据为近地点高度≤200km[9]。

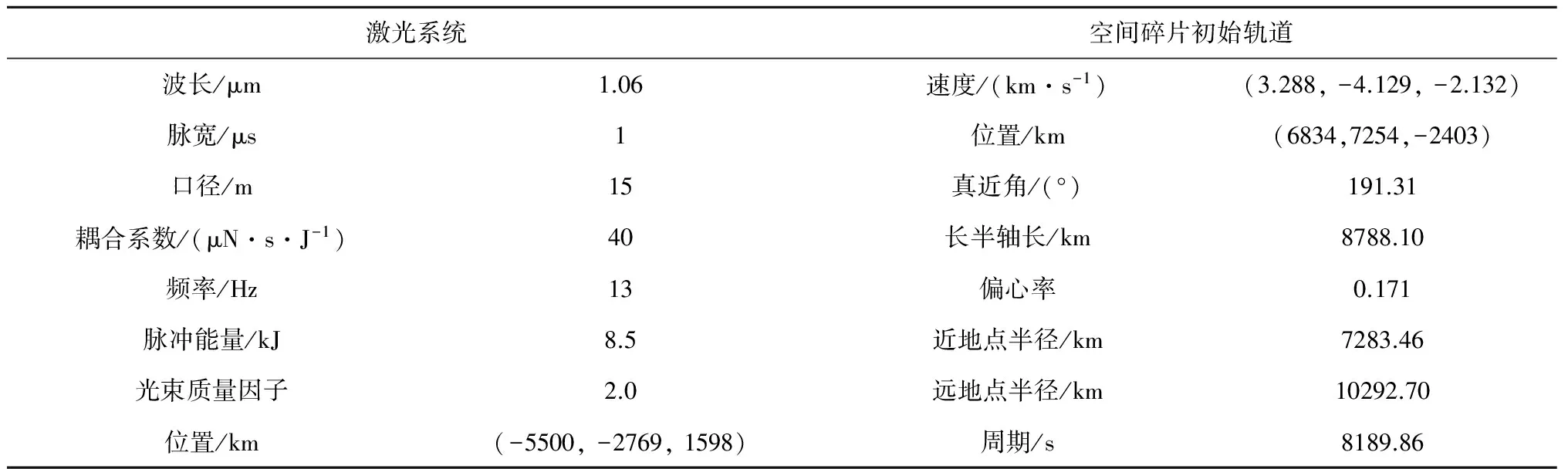
表1 地基激光系统和空间碎片相关参数

计算结果表明，碎片的初始位置不在激光的作用范围内。碎片移动4145.54s后，在位置(-5852.6,-3837.3,2361.7)处进入激光作用范围(此时天顶角为45°)。表2为计算结果，结果表明：对于具有相同轨道参数、材质、形状和姿态的碎片，随着碎片直径的增加，移除所需要的时间增加，过顶次数增加。在本文的算例中，对于1mm的碎片，能够利用394次脉冲在一次过顶中被移除；而10cm的碎片，则需要19次过顶39636次脉冲，经历154172s才能被移除。采用100kW左右的激光装置，能在2～3天、19次过顶之内移除0.1～10cm的碎片。表3为移除过程中关键点的实时信息。图2(a)为图形化输出结果，其中黑色圆点为激光站位置，灰色圆点为碎片初次变轨位置。

表2 激光移除碎片所需的过顶/交会次数，脉冲次数和时间

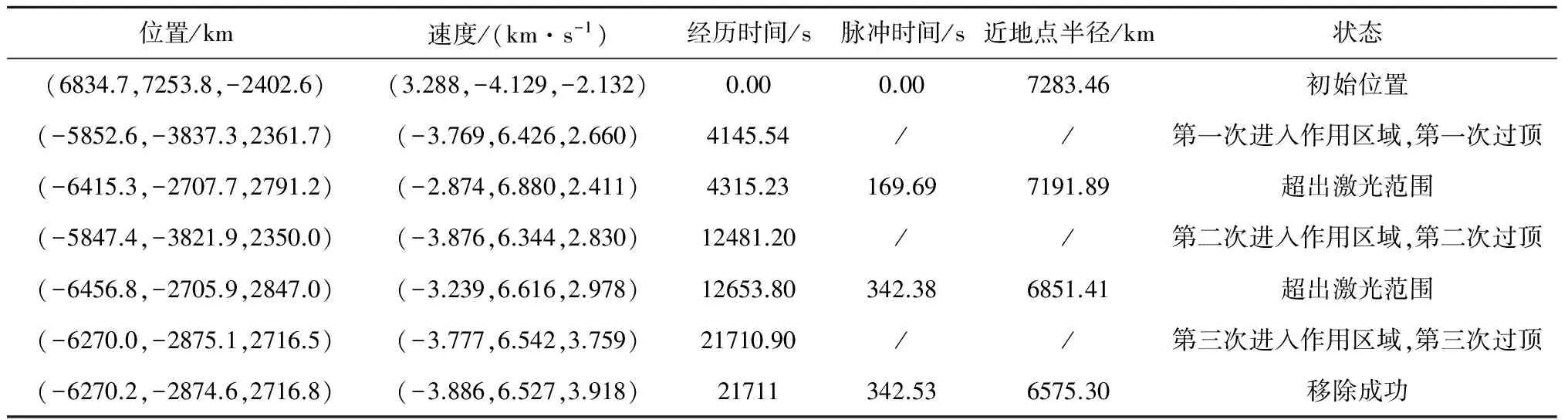
表3 直径1cm碎片的移除过程(地基)

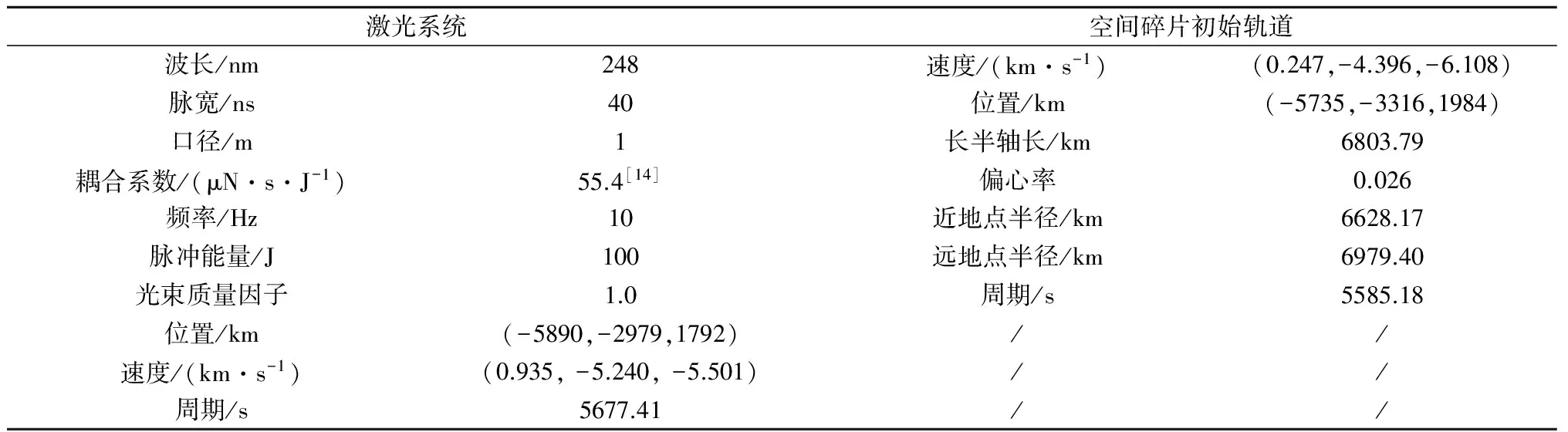
表4 天基激光系统和碎片初始轨道参数

在天基系统中，我们采用波长为248nm的近紫外激光，激光卫星和空间碎片的初始轨道参数见表4，其中耦合系数来源于文献[19]。结果表明：碎片的初始位置不在激光的作用范围内，经过143.7 s，碎片在位置(-5678.3, -3722.3, 1383.1)处进入激光(-5765.3, -3467.9, 1250.0)作用范围(此时距离为300km)。计算结果列于表2，对于具有相同初始状态的碎片，随着碎片直径的增加，移除所需要的时间增加，交会次数增加。在本文的算例中，采用1kW的激光装置，在一次交会中就能移除1 cm的碎片，对于较大碎片需要多次交会。天基所需激光系统功率远低于地基系统，移除效率明显高于后者。图2(b)为移除1 cm碎片的图形化输出结果。

3 常见空间碎片的移除效果

在Orion项目中[8]将空间碎片分为5大类：Na/K冷却剂、碳酚醛树脂、多层绝缘材料(MLI)、铝和钢。不同的材料具有不同的移除效果，本文计算了这些常见空间碎片的移除过程，碎片参数取自文献[9]。假设激光始终垂直辐照在全部截面上，计算结果见表5。可以发现钢材料的移除难度最大，多层绝缘材料最容易被移除。本文算例中，对于天基系统，利用表4中的激光参数，能够移除所有碎片。对于地基，利用110.5kW的激光装置，能够移除除钢材料之外的全部碎片。在三维空间中，由于速度增量不一定在碎片轨道平面上，向外的速度分量使轨道倾角增大，在多脉冲长时间作用下使碎片逃逸出激光站的作用范围，无法达到移除碎片的目的。因此，在实际操作中应选择合适的作用位置和激光脉冲参数。

从表5可以看出，天基系统对激光系统的功率需求远小于地基系统，天基1kW的激光能够在三次交会中移除所有碎片，获得优于地基110.5kW的移除效果，并且移除效率远远高于后者。

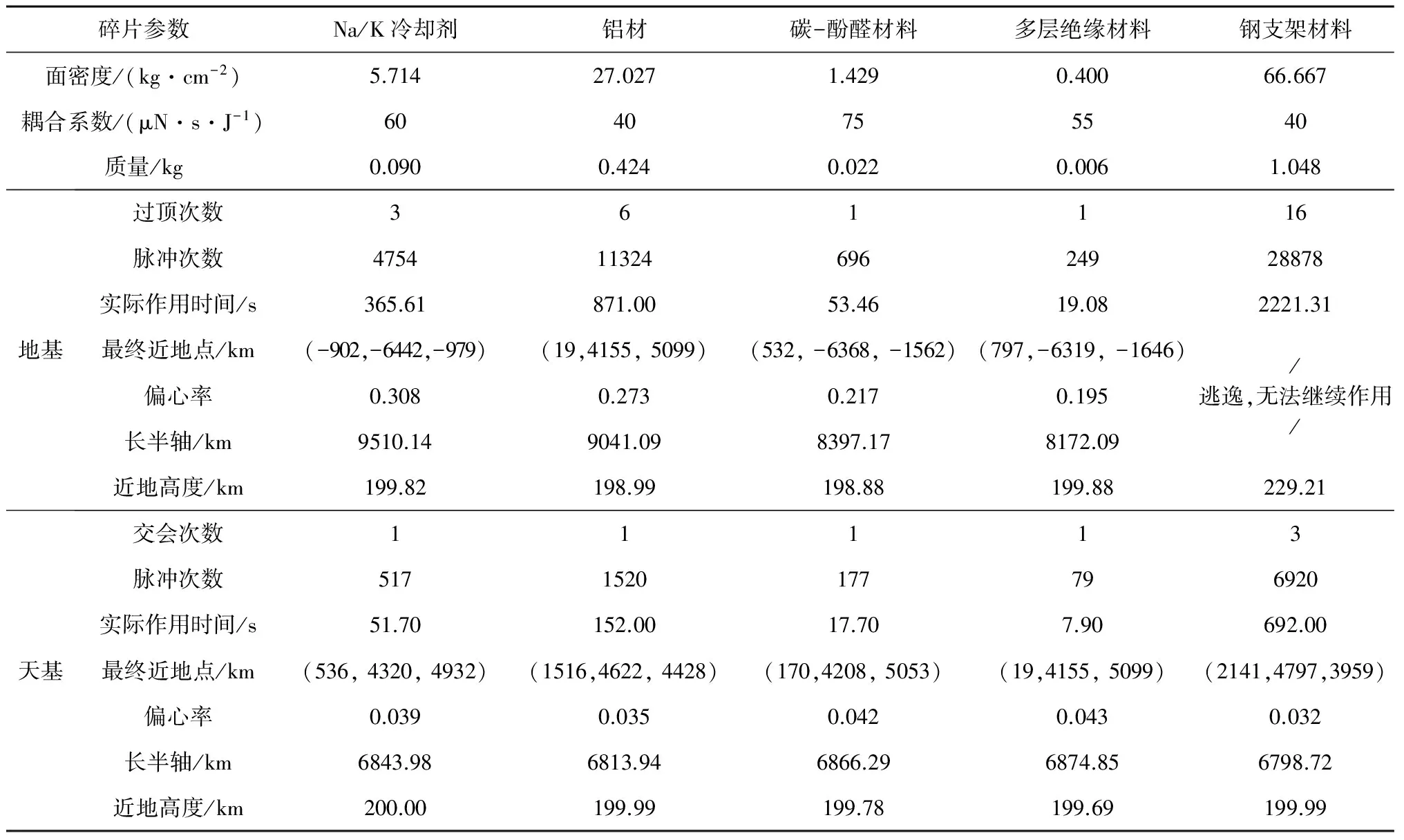
表5 地基和天基系统移除5种常见空间碎片的效果

4 结 论

本文建立了适用于地基和天基激光移除空间碎片系统的三维仿真模型。该模型能够根据输入的激光(能量、频率、波长、位置矢量等)和碎片参数(耦合系数，位置矢量，速度矢量等)，计算碎片的变轨过程，实时输出碎片的轨道信息和移除结果。

采用该模型计算了波长为1.06μm的近红外地基系统和波长为246nm的近紫外天基系统移除碎片的过程。结果表明：天基系统对激光系统的功率需求远小于地基系统。在本文的算例中，采用100kW左右的地基激光装置，能在2～3天、19次过顶之内移除给定轨道上0.1～10cm的铝碎片。采用1kW的天基激光装置，在一次交会中就能移除给定轨道上1cm的铝碎片，对于较大碎片需要多次交会。不同材料具有不同的移除效果，其中钢材料的移除难度最大，多层绝缘材料最容易被移除。由于存在轨道倾角，向外的速度增量分量使轨道倾角增大，在多脉冲的作用下可能使碎片逃逸出激光站/卫星的作用范围。

[1] Weeden B. Overview of the legal and policy challenges of orbital debris removal [J]. Space Policy, 2011, 27(1): 38-43.

[2] White A E, Lewis H G. The many futures of active debris removal [J]. Acta Astronautica, 2014, 95: 189-197.

[3] Levin E, Pearson J, Carroll J. Wholesale debris removal from LEO [J]. Acta Astronautica, 2012, 73: 100-108.

[4] 陈钦, 杨乐平. 空间绳网系统发射动力学问题研究[J]. 宇航学报, 2009，30(5): 1829-1833. [Chen Qin, Yang Le-ping. Research on casting dynamics of orbital net systems [J]. Journal of Astronautics, 2009, 30(5): 1829-1833.]

[5] 刘志新, 游秀杨, 洪玖, 等. 基于扩张状态观测器的空间飞网捕捉系统参数估计[J]. 宇航学报, 2014, 35(2): 906-915. [Liu Zhi-xin，You Xiu-yang，Hong Jiu，et al. The Parameter estimation based on extended state observerfor space net capture system [J]. Journal of Astronautics, 2014, 35(2): 906-915.]

[6] Phipps C R, Baker K L, Libby S B, et al. A laser optical system to remove low Earth orbit space debris[C]. Sixth European Conference on Space Debris, Darmstadt, Germany, April 22-25, 2013.

[7] Choi S H, Pappa R S. Assessment study of small space debris removal by laser satellites [C]. 2011 IEEE Aerospace Conference, Montana, USA, March 5-12, 2011.

[8] Campbell J W. Project ORION: orbital debris removal using ground-based sensors and lasers [R]. NASA Technical Memorandum 108522, 1996.

[9] Phipps C R, Friedman H, Gavel D, et al. ORION: clearing near-Earth space debris using a 20 kW, 530 nm Earth-based, repetitively pulsed laser [J]. Laser Particle Beams, 1996, 14(1): 1-44.

[10] Esmiller B, Jacquelard C. CLEANSPACE “Small debris removal by laser illumination and complementary technologies”[J]. AIP Conference Proceedings, 2011, 1402(1): 347.

[11] 袁振涛, 胡卫东, 郁文贤. 电子篱笆型空间监视雷达测向数据关联算法[J]. 宇航学报, 2009, 30(5): 1972-1978. [Yuan Zhen-tao, Hu Wei-dong, Yu Wen-xian. Direction data association in NAVSPASUR-type space surveillance radar[J]. Journal of Astronautics, 2009, 30(5): 1972-1978.]

[12] 李冬, 易东云, 程洪玮. 天基空间目标监视的短弧段定轨技术[J]. 宇航学报, 2011, 32(11): 2339-2345. [Li Dong, Yi Dong-yun, Cheng Hong-wei. Orbit determination with short arcs for space-based space object surveillance [J]. Journal of Astronautics, 2011, 32(11): 2339-2345.]

[13] 翟光, 张景瑞. 空间非合作目标快速姿态跟踪导航方法研究[J]. 宇航学报, 2013, 34(3): 362-368. [Zhai Guang, Zhang Jing-rui. Research on rapid attitude tracking for space non-cooperative target [J]. Journal of Astronautics, 2013, 34(3): 362-368.]

[14] 常浩, 金星, 洪延姬, 等. 地基激光清除空间碎片过程建模与仿真[J]. 航空学报, 2012, 33(6): 994-1001. [Chang Hao, Jin Xing, Hong Yan-ji, et al. Modeling and simulation on ground-based lasers cleaning space debris [J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(6): 994-1001.]

[15] Rubenchik A M, Erlandson A C, Liedahl D. Laser system for space debris cleaning [J]. AIP Conference Proceedings, 2012, 1464(1): 448-455.

[16] Phipps C R, Baker K L, Libby S B, et al. Removing orbital debris with lasers [J]. Advances in Space Research, 2012, 49: 1283-1300.

[17] Curtis H D. Review of orbital mechanics for engineering students [J]. Journal of Guidance, Control, and Dynamics, 2008, 21(2): 445-446.

[18] 洪延姬, 金星. 激光清除空间碎片方法[M]. 国防工业出版社, 2013.

[19] Phipps C. An alternate treatment of the vapor-plasma transition [J]. International Journal of Aerospace Innovations, 2011, 3(1): 45-50.

[20] Phipps C, Turner T P, Harrison R F, et al. Spicochi. Impulse coupling to targets in vacuum by KrF, HF and CO2 lasers [J]. J. Appl. Phys., 1988, 64(3): 1083-1096.

[21] Phipps C R. A laser-optical system to re-enter or lower low Earth orbit space debris [J]. Acta Astronautica, 2014, 93: 418-429.

[22] Liedahl D A, Libby S B, Rubenchik A. Momentum transfer by laser ablation of irregularly shaped space debris [J]. AIP Conf. Proc., 2010, 1278(1): 772-779.

[23] 金星, 常浩, 洪延姬, 等. 激光辐照不规则空间碎片冲量矢量计算[J].强激光与粒子束, 2012, 24(8):1956-1960. [Jin Xing, Chang Hao, Hong Yan-ji, et al. Impulse calculation for irregularly shaped space debris under laser irradiation[J]. High Power Laser and Particle Beams, 2012, 24(8): 1956-1960.]

通信地址：北京市海淀区友谊路104号(100094)

电话：(010)68745870

E-mail:zhangpinliang620@126.com

(编辑：牛苗苗)

Three-Dimensional Simulation and Modeling on Removing Orbital Debris with Lasers

ZHANG Pin-liang, GONG Zi-zheng, YANG Wu-lin, CHEN Chuan

(Beijing Institute of Spacecraft Environment Engineering, Beijing 100094, China)

This paper establishes a laser irradiation three-dimensional orbit dynamic model based on the theory of orbital mechanics and the interaction effects between laser and matters. With the position vector and velocity vector regarded as the initial data, and setting the parameters of laser, this model calculates the velocity and provides the real-time updates, which can actually reflect the process of the debris removal. It contains the ground-based and space-based models, both of them can output the orbit information of the debris real-time updates, and the graphical output directly displays the process of the orbital transfer. The effect of the velocity increment component on the orbit inclination is taken into consideration, thus this model can deal with the situation of the debris escape. Moreover, we successfully calculate the removal process and the result of various debris using ground-/space-based model. We suppose that it is the most difficult to remove steel, while multilayered insulation removal is the most efficient.

Laser ablation; Space debris; Orbital transfer; 3D simulation; Numerical model

2016-11-14;

2017-01-12

V416.5; TN249

A

1000-1328(2017)03-0323-08

10.3873/j.issn.1000-1328.2017.03.014

张品亮(1986-)，男，博士，工程师，主要从事航天器空间碎片防护、空间碎片移除、材料动态力学性能和高压物理等研究。