基于神经网络的RLV再入段有限时间自适应姿态控制
陈 辰,吕跃勇,马广富,王润驰
(哈尔滨工业大学控制科学与工程系,哈尔滨150001)
基于神经网络的RLV再入段有限时间自适应姿态控制
陈 辰,吕跃勇,马广富,王润驰
(哈尔滨工业大学控制科学与工程系,哈尔滨150001)
针对可重复使用运载器(RLV)再入段的姿态控制问题,提出了一种基于神经网络的有限时间自适应姿态跟踪控制方法。首先,在传统RLV建模的基础上将模型不确定性、耦合及扰动力矩分离作为复合扰动;然后,利用径向基神经网络(RBFNN)对其在线估计并在标称控制器中进行动态前馈补偿;最后,利用终端吸引子改进控制器实现了对期望状态的有限时间跟踪,并通过引入鲁棒项降低了RBFNN估计误差对控制精度的影响。设计的姿态控制器无需获知精确的气动数据与扰动范围而仅需某飞行状态下的标称值。仿真结果表明提出的控制方法对RLV再入姿态跟踪具有较好的控制效果。
可重复使用运载器;神经网络;自适应估计;有限时间稳定
0 引 言
RLV等高超声速飞行器再入返回过程中跨越临近空间,由于这一区域气压和大气密度变化剧烈,加之高速飞行引起飞行器表面烧蚀和变形,因此很难通过地面试验获得准确的气动特性数据[1]。伴随飞行状态的改变,飞行器动力学特性变化显著,各通道间耦合特性、模型不确定性对控制系统影响也愈发明显,这些都为再入段姿态控制系统的设计带来了更多的挑战[2]。
对于上述非线性问题,自适应控制[3]和扰动观测器是处理系统不确定性以及提高鲁棒性的常用方法。文献[3]结合高超声速飞行器特征模型,设计了全通道自适应控制器。文献[4]将自适应与反步控制相结合,实现了对不确定项未知边界的估计,并引入鲁棒项进一步抑制了扰动。非线性扰动观测器[5]、滑模扰动观测器[6]与反步控制、最优控制相结合能够有效抑制复合扰动,提高系统动态性能。
神经网络估计技术具备对任意非线性连续函数的智能逼近能力,可以对外界干扰、非线性动态等系统不确定性进行有效估计;神经网络控制策略不依赖于系统扰动或不确定性的阈值具有更好的鲁棒性和容错性,且采用权值自适应律可以实时调整控制器参数从而保证网络的逼近性能,因此在飞行控制系统设计中得到了广泛应用[7]。文献[8]将自适应RBF用于逼近模型不确定性部分,结合动态面控制方法实现了航迹角轨迹跟踪控制;文献[9]采用神经网络干扰观测器对动态逆误差进行在线逼近并补偿。文献[10] 基于神经网络观测器对气动建模误差进行补偿,并以F-16气动模型为例验证了姿态控制系统的有效性。文献[11]将单隐层神经网络与自适应律相结合来修正动态逆的近似误差,在输入饱和条件下设计了姿态控制器。
需要指出,上述方法均易受到神经网络估计误差的影响,且仅能保证系统渐近稳定,收敛时间较长,不利于处理RLV的快时变特性。相比之下,有限时间控制能够使系统在有限时间内收敛,具有良好的快速性和抗扰动性,对于处理RLV的快时变特性具有明显优势[12]。文献[13]基于高阶滑模控制技术设计时标分离条件下的内外环控制器,解决了存在参数不确定性和外界扰动的再入姿态有限时间控制问题。文献[14]针对系统不确定性和外界扰动设计了准连续高阶滑模姿态控制器,实现了对制导指令的有限时间跟踪。终端滑模面中的终端吸引子[15]是使系统具备有限时间收敛特性的主要原因,以此为基础的终端滑模控制方法在有限时间控制领域得到了广泛研究。
基于上述研究,本文提出了一种基于RBF神经网络的RLV再入姿态自适应鲁棒控制方案。首先将未建模动态,不确定项,耦合影响,参数摄动等扰动转化为复合扰动,建立了用于控制器设计的 RLV 再入姿态模型;然后,设计了RBF神经网络自适应估计器,对复合扰动进行在线估计并前馈补偿;最后,针对神经网络估计误差引入终端吸引子与鲁棒项,提出了一种改进的有限时间神经网络鲁棒姿态控制器,使系统跟踪误差有限时间收敛。数值仿真验证了本文所提出控制策略的有效性。
1 RLV再入姿态数学模型及问题描述
忽略地球自转影响,再入段RLV姿态模型为[1]:
(1)
(2)
式中:Ω=[αβμ]T,α,β和μ分别为攻角,侧滑角和倾侧角;ω=[ωxωyωz]T,ωx,ωy和ωz分别是滚转角速率,偏航角速率和俯仰角速率;δ=[δeδaδr]T,δe,δa和δr分别为左右升降舵副翼和方向舵偏角。fs=[fαfβfμ]T以及ff=[fωxfωyfωz]T具体表达式如下:
(3)
(4)
式中:X,Y和Z分别为阻力、升力和侧向力,l,m和n分别为滚转、偏航和俯仰力矩。V为飞行器速率,S为参考面积,b为翼展长度,M为飞行器质量,Ix,Iy和Iz分别为三轴的转动惯量。Xcg为参考力矩中心到重心距离,θ为弹道倾角,q=0.5ρV2为动压,ρ为大气密度。gs1,gs2,gf为3×3的矩阵,具体表达式为:
(5)
(6)
(7)
式中:gi,j为气动系数项,具体参数见文献[1]。在一般研究中,由于角速度变量响应较快而角度动态响应较慢,因此式(1)常被称为外环或慢回路,式(2)常被称为内环或快回路。
由式(1)~(4)可以看出,高超声速飞行器再入飞行姿态动力学模型具有复杂非线性、三通道强耦合的特点。由于已知真实飞行试验数据的不足,很难建立精确的数学模型,因此控制器设计应该充分考虑系统的不确定性以及扰动对控制系统的影响。为此对模型做如下数学变换,以外环慢回路模型为例,由于未建模动态参数摄动及不确定性主要包含于fs(Ω)中,因此用fs(Ω)+Δfs(Ω)表示,其中Δfs(Ω)为不确定项。假设ds为外环扰动项。则方程(1)等效为:
(8)
式中:h1(t)=Δfs(Ω)+gs2δ+ds,u1=gs1ω。
对于内环快回路模型,主要存在力矩扰动,系统未建模动态、气动参数的不确定性,主要包含在ff(Ω,ω)中,因此用ff(Ω,ω)+Δff(Ω,ω)表示。对于内环的控制输入矩阵gf由于很难精确获知舵的气动特性,因此我们用标称值gf0来近似,df为内环扰动项,于是得到内环面向控制的动态模型
(9)
式中:h2(t)=Δff(Ω,ω)+(gf-gf0)δ+df,u2=gf0δ。至此,得到了用于本文神经网络控制器设计的再入姿态运动方程。
2 姿态控制器设计
姿态控制的主要目的为实现对期望姿态角指令Ωd的跟踪。根据时标分离原则,对外环回路设计所需要的姿态角速率指令ωc,称为慢回路控制器;再对内环回路设计控制舵偏量δ,称为快回路控制器。通过合理设计内外环增益,保证满足时标分离条件,则在慢回路控制器设计时可忽略快回路动态特性,对ωc和δ分别独立设计。系统控制结构如图 1 所示。由动力学模型(1)~(2)式可知,双环的控制器设计过程类似,因此以外环控制器设计为例给出设计过程。
为方便系统稳定性分析,给出如下引理及定义,
引理1[12]. 考虑如下系统:
假设存在连续可微函数V(x):u→R满足下列条件:
1.V(x)为正定函数,
2.存在正实数c>0和α∈(0,1),以及一个包含原点的开邻域U0∈U,使得下列条件成立:
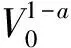
引理2[16]. 对于任意实数li∈R,i=1,…,n,0 引理3[17]. 根据RBF神经网络的局部特性,径向基函数网络在有足够多的节点,且有适当构建的节点中心及中心宽度的情况下,能够对任意连续函数Q(X)在有界闭集ΩX内任意逼近,存在如下表达式: 定义如下吸引子函数: 2.1 神经网络姿态控制器设计 首先对系统(8)设计如下的标称控制器: (10) 式中:e=Ω-Ωd为姿态角跟踪误差,增益值ks为: ks=diag(ks,α,ks,β,ks,μ),ks,α,ks,β,ks,μ>0 (11) (12) (13) 从式(13)可以看出,控制器的构成只需要系统标称模型,降低了对飞行器模型精确度的要求。 2.2RBF神经网络控制系统稳定性分析 为了分析系统的稳定性,根据RBF神经网络对连续非线性函数具有全局任意精度逼近的能力,给出如下假设: 首先,构造如下Lyapunov函数: (14) (15) 对式(14)求导可得: (16) 将式(13)代入式(8),可得系统误差动态方程: (17) 代入式(16),可得 (18) ks为正定对称阵,因此存在正定矩阵P,Q满足如下Lyapunov方程 (19) 结合式(18)可知: (20) (21) 设计如下神经网络自适应律: (22) 代入式(21)可得: (23) (24) 由式(24)可知,Q的最小特征值越大,P的最大特征值越小,系统跟踪误差e的收敛半径越小,跟踪精度越高。同时从收敛域可以看出,较大的神经网络逼近误差η0也会加大误差收敛半径,因此有必要对控制器进行改进,提高控制器对神经网络逼近误差的鲁棒性。 2.3 有限时间RBF神经网络姿态控制器设计 从第2.2节分析过程可知,跟踪误差指数收敛但存在稳态误差,当神经网络逼近误差较大时必将恶化系统的跟踪效果,因此为了加快系统状态的跟踪速度达到有限时间稳定,并且消除系统稳态误差,设计新的控制器: (25) 式中: v1是为实现有限时间稳定而引入的终端吸引子,v2为鲁棒控制项,用于消除权值估计误差产生的逼近误差。ks1,ks2为增益矩阵,定义如下:ks1=diag(ks1,α,ks1,β,ks1,μ),ks2=diag(ks2,α,ks2,β,ks2,μ),ksi,α,ksi,β,ksi,μ>0,i=1, 2。 (26) 利用Lyapunov方法对采用新控制器(25)式作用下的系统进行稳定性分析。 第一步:首先选取如下Lyapunov函数: (27) 对上式求导可得: (28) 将误差动态(26)代入式(28),经过与式(16)~(23)类似的数学推理方法可得: (29) 当取参数满足条件:λmin(Pks2)≥η0λmax(P)时可得 (30) 即系统全局稳定。 第二步:定义如下Lyapunov函数: (31) 对上式求导并结合误差方程(26)式,可得 (32) 进一步数学处理,可得 (33) (34) 由引理2可知 (35) 从以上分析过程可知,在控制器式(25)作用下,系统误差有限时间收敛至零,消除了神经网络逼近过程中稳态误差对控制系统的影响。同理,根据时标分离原则,针对快回路式(9)设计神经网络有限时间控制器: δ*=δ+vω1+vω2 (36) 式中: (37) (38) 其中,τ为滤波参数。vω1和vω2表达式如下: (39) 内环控制器中神经网络自适应律设计为: (40) γ2>0,kf 0,kf 1,kf 2分别为内环增益,反馈控制项系数和鲁棒控制项系数,kf 0=diag(kf 01,kf 02,kf 03),kf 1=diag(kf11,kf12,kf13),kf 2=diag(kf 21,kf 22,kf 23),kfij>0,i=0,1,2,j=1,2,3。 [18]中的飞行器模型基础参数。合理选择RLV仿真初始条件:h(0)=50km,α(0)=0°,β(0)=0° ,μ(0)=0°,[ωx0ωy0ωz0]=[0 0 0]Trad/s。控制器参数选取如表1所示,以满足系统稳定性要求。 表1 控制系统参数 标称值gf0取为: 神经网络节点取为6个,节点中心选为0,初始化RBF神经网络输出矩阵为0。 内环扰动项表达式如下: (41) 系统攻角和倾侧角输入指令为幅值10°的方波信号,由于飞行器BTT的转弯要求,侧滑角指令设置为0°。 考虑内环扰动(41)式情况下系统响应如图2和图3所示,图2为对期望姿态角的跟踪曲线,对比未加补偿控制器,可以看出带有神经网络补偿的两种控制器对于方波信号均具有较好的跟踪效果,改进控制律FTRBFNN在跟踪时间和精度上都有很大提升,跟踪误差幅值小于0.1,通道之间解耦效果更好,控制性能进一步提升。从两种控制器作用下的系统控制输入图3可以看出,控制输入均在执行机构限幅之内,有效实现了再入姿态跟踪控制。控制输入舵偏角中峰值的出现是由于方波信号的不连续造成,实际系统中对指令信号会进行滤波和平滑处理,这里仅给出最苛刻的跟踪仿真分析。 图4为神经网络对内环扰动的观测值,从图中可以看出,神经网络能够快速对扰动进行观测,并且在放宽RBF参数条件下,观测器存在观测误差,RBFNN和FTRBFNN两种控制器作用下,RBFNN观测效果基本一致,对比图2可以得出,引入鲁棒项的FTRBFNN能够消除误差的影响,有效提高扰动环境下的姿态控制精度,具有更好的控制性能。 本文针对RLV再入飞行的姿态控制问题,提出一种基于RBF神经网络的有限时间自适应控制方法。该方法能够利用RBF神经网络对由系统不确定性、动力学耦合项和干扰形成的复合扰动进行自适应估计,控制器设计只需使用系统标称值而无需精确的气动模型参数,极大减小了对系统精确模型的依赖,简化了控制器设计。进一步引入的终端吸引子和鲁棒控制项则在赋予系统有限时间收敛特性的同时,进一步降低了自适应估计误差对控制精度的影响。仿真结果表明,本文提出的基于RBF神经网络的有限时间自适应控制器能够快速无超调地跟踪期望指令,控制系统具有较好的鲁棒性。 参 考 文 献 [1] 李惠峰. 高超声速飞行器制导与控制技术[M]. 北京: 宇航出版社, 2012. [2] 张天翼, 周军, 郭建国. 高超声速飞行器鲁棒自适应控制律设计 [J]. 宇航学报, 2013, 34(3): 384-388. [ZhangTian-yi,ZhouJun,GuoJian-guo.Astudyonrobustadaptivecontrolmethodforhypersonicvehicle[J].JournalofAstronautics. 2013, 34(3): 384-388.] [3] 杜立夫, 黄万伟, 刘晓东, 等. 考虑特征模型的高超声速飞行器全通道自适应控制 [J]. 宇航学报, 2016, 37(6): 711-719. [DuLi-fu,HuangWan-wei,LiuXiao-dong,etal.Whole-channeladaptivecontrolforhypersonicvehicleconsideringcharacteristicmodel[J].JournalofAstronautics. 2016, 37(6): 711-719.] [4] 王芳, 宗群, 田栢苓, 等. 基于鲁棒自适应反步的可重复使用飞行器再入姿态控制[J]. 控制与决策, 2014, 29(1): 12-18. [WangFang,ZongQun,TianBai-ling,etal.Robustadaptiveback-steppingflightcontroldesignforreentryRLV[J].ControlandDecision, 2014, 29(1): 12-18.] [5] 余光学, 李惠峰.RLV抗扰动非线性最优控制器设计[J]. 控制与决策, 2015, 30(3): 513-519. [YuGuang-xue,LiHui-feng.Anti-disturbancenonlinearoptimalcontrollerdesignforRLV[J].ControlandDecision. 2015, 30(3):513-519.] [6] 程路, 姜长生, 都延丽, 等. 基于滑模干扰观测器的近空间飞行器非线性广义预测控制[J]. 宇航学报, 2010, 31(2): 423-431. [ChengLu,JiangChang-sheng,DuYan-li,etal.TheresearchofSMDObasedNGPCmethodforNSVcontrolsystem[J].JournalofAstronautics. 2010, 31(2): 423-431] [7] 周丽, 姜长生, 钱承山. 一种基于神经网络的快速回馈递推自适应控制[J]. 宇航学报, 2008, 29(6): 1888-1894. [ZhouLi,JiangChang-sheng,QianCheng-shan.Afastadaptivebacksteppingmethodbasedonneuralnetworks[J].JournalofAstronautics. 2008, 29(6): 1888-1894.] [8]GuoY,LiuJ.Neuralnetworkbasedadaptivedynamicsurfacecontrolforflightpathangle[C].The51stIEEEConferenceonDecisionandControl,Hawill,USA, 2012, 8350(2): 5374-5379. [9] 陈谋, 邹庆元, 姜长生, 等. 基于神经网络干扰观测器的动态逆飞行控制[J]. 控制与决策, 2008, 23(3): 283-287. [ChenMou,ZouQing-yuan,JiangChang-sheng,etal.Dynamicalinversionflightcontrolbasedonneuralnetworkdisturbanceobserver[J].ControlandDecision,2008, 23(3): 283-287.] [10]LeeT,KimY.Nonlinearadaptiveflightcontrolusingbacksteppingandneuralnetworkscontroller[J].JournalofGuidance,Control,andDynamics, 2012, 24(4): 675-682. [11]JohnsonEN,CaliseAJ.Limitedauthorityadaptiveflightcontrolforreusablelaunchvehicles[J].JournalofGuidance,Control,andDynamics, 2003, 26(6): 906-913. [12] 丁世宏, 李世华. 有限时间控制问题综述[J]. 控制与决策, 2011, 26(2): 161-169. [DingShi-hong,LiShi-hua.Asurveyforfinite-timecontrolproblems[J].ControlandDecision, 2011, 26(2): 161-169.] [13] 范金锁, 张合新, 张明宽, 等. 基于自适应二阶终端滑模的飞行器再入姿态控制[J]. 控制与决策, 2012, 27(3): 403-407.[FanJin-suo,ZhangHe-xin,ZhangMing-kuan,etal.Adaptivesecond-orderterminalslidingmodecontrolforaircraftre-entryattitude[J].ControlandDecision, 2012, 27(3): 403-407.] [14] 王婕, 宗群, 田栢苓, 等. 基于拟连续高阶滑模的高超声速飞行器再入姿态控制[J]. 控制理论与应用, 2014, 31(9): 1166-1173.[WangJie,ZongQun,TianBai-ling,etal,Reentryattitudecontrolforhypersonicvehiclebasedonquasi-continuoushighorderslidingmode[J].ControlTheory&Applications, 2014, 31(9): 1166-1173.] [15]ZakM.Terminalattractorsinneuralnetworks[J].NeuralNetworks, 1989, 2(4): 259-274. [16]YuSH,YuXH,ShirinzadehB,etal.Continuousfinitetimecontrolforroboticmanipulatorswithterminalslidingmode[J].Automatica, 2005, 11(41): 1957-1964. [17]ParkJH,SandbergIW.Universalapproximationusingradial-basis-functionnetworks[J].NeuralComputation, 2008, 3(2): 246-257. [18] 王建华, 刘鲁华, 汤国建. 高超声速飞行器俯冲段制导与姿控系统设计[J]. 宇航学报, 2016, 37(8): 964-973. [WangJian-hua,LiuLu-hua,TangGuo-jian.Guidanceandattitudecontrolsystemdesignforhypersonicvehicleindivephase[J].JournalofAstronautics, 2016, 37(8): 964-973.] 通信地址:黑龙江省哈尔滨市香坊区一匡街2号,哈尔滨工业大学科学园2B栋322室 电话:(0451)86418320-322 E-mail:chenchen@hit.edu.cn 吕跃勇(1983-),男,助理研究员,主要从事导航、制导与控制、编队飞行控制方面研究。本文通信作者。 通信地址:黑龙江省哈尔滨市香坊区一匡街2号,哈尔滨工业大学科学园2B栋322室(150001) 电话:(0451)86418320-322 E-mail:lvyy@hit.edu.cn (编辑:张宇平) Neural Network Based Finite-Time-Stable Adaptive Attitude Control for RLV Reentry CHEN Chen, LV Yue-yong, MA Guang-fu, WANG Run-chi (Department of Control Science and Engineering, Harbin Institute of Technology, Harbin 150001, China) A neural network based finite-time-stable adaptive attitude control strategy for a reusable launch vehicle (RLV) reentry is proposed. Firstly, the traditional RLV dynamic model is improved by separating out the uncertainty, coupled dynamic and disturbance together as combined disturbance. Then, adaptive estimation for the combined disturbance based on radical basis function neural network (RBFNN) is introduced into a nominal controller as feed-forward compensation. Moreover, the terminal attractor is used to improve the controller so that the desired system state could be tracked in finite time, and a robust control function is also introduced so as to reduce the impact on control accuracy from the error of RBFNN estimation. Only the nominal parameters of the system rather than the precise value and bounds of disturbance are utilized for the proposed controller. Finally, the effectiveness of the controller is demonstrated by the numerical simulations. Reusable launch vehicle; Neural network; Adaptive estimation; Finite time stable 2016-05-21; 2016-11-29 国家自然科学基金(61673135, 61603114,61403103) V448.2 A 1000-1328(2017)03-0279-08 10.3873/j.issn.1000-1328.2017.03.008 陈 辰(1987-),男,博士生,主要从事飞行器姿态控制,鲁棒非线性控制。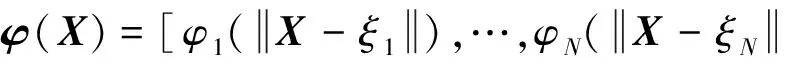


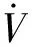
3 仿真分析
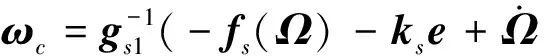

4 结 论

