矿用汽车转向机构仿真与优化

太原重工股份有限公司技术中心　朱涛

一、引言

煤炭和铁矿是支撑全球经济发展的重要资源，其开采及运输工作是高效开发利用矿产资源的重要环节。矿用汽车作为主要运输工具，运输着露天矿区40%的煤炭及90%的铁矿，同时在大型水利工程建设行业中也有着广阔的发展空间。矿用汽车被广泛应用于煤、铁、铜、铝和油砂等各种露天矿山的运输任务中，这些工程场所路况差、坡路较多而且环境恶劣复杂，往往是连续满载上坡，而下坡时又必须连续制动，因此对矿用汽车的使用安全性及可靠性要求很高。同时，由于重型矿用汽车批量小，造价非常高，对道路又有一定的要求，所以无法像公路车辆一样可以在实验室进行零部件和整车试验，通过试验来评价和改进设计。因此，在矿用汽车的开发设计过程中，计算机辅助工程技术得到越来越多的应用，这对缩短开发设计周期和节约生产成本意义重大。

转向机构作为矿用汽车的重要组成部分，用来改变或恢复其行驶方向，对行驶安全至关重要。转向机构的设计影响着矿用汽车的平顺性、安全性、操纵稳定性及轮胎的寿命。良好的转向梯形机构能够减小行驶阻力，使转向轻便，并减小轮胎磨损。对转向梯形机构的运动学相关问题进行研究，并对机构进行优化。这种方法使得结构设计过程更加人性化和科学化，同时为矿用汽车的设计提供参考。

二、 转向梯形机构运动学分析

转向梯形机构主要由汽车前轴、转向节臂和转向横拉杆组成，如图1所示。转向动力缸推动转向节臂，转向节臂再推动转向横拉杆，从而带动转向横拉杆的摆动，实现矿用汽车的转向。

转向梯形机构的设计直接影响着矿用汽车的转向性能。合理的转向梯形机构对提高汽车的安全性至关重要。特别是在矿山这种路况差的运输环境，如果发生危险，将造成巨大损失，因此安全性要求很高。

图1 转向梯形结构

若要保证汽车在转弯时能够顺利转弯，两侧转向轮的偏转角度必须按一定关系变化，才能使汽车转向时车轮与地面的相对滑动尽可能小，不发生侧滑。转向梯形机构用来确保汽车转弯行驶时，所有车轮都能绕同一瞬时转动中心，在不同的圆周上作无滑动的纯滚动，即符合阿克曼理论转向特性，如图2所示。设φi、φo分别为内、外转向车轮转角，K为两个转向节中心点的距离，L为汽车轴距。则理想的内、外转向车轮的转角有如下关系：

若假设自变量为φo，依据阿克曼理论转向关系，可以得出因变量φi的理想值为：

从图2中我们可以得出最小转弯半径Rmin满足下列关系式：

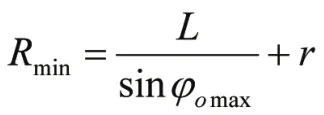
图2 阿克曼转向关系图

式中：r为转向轮绕主销转动半径（又称车轮转臂），设计值为0.92m。在给定最小转弯半径Rmin=14.5m的条件下，我们可以计算出外轮最大转角φomax=27.8°，内侧车轮最大转角理论值为φimax=38.4°。

建立转向梯形平面数学模型。由图3可知，只要确定转向节臂长度m和梯形底角β，就可以确定整个转向梯形机构。

图3转向梯形机构示意图

设φo为外侧车轮转角，φi’为内侧车轮实际转角，根据图中几何关系，可以推导出实际转向过程中内侧车轮转角与外侧车轮转角之间的关系。在汽车转向过程中，所设计的转向梯形机构给出的实际内侧车轮转角φi’应尽可能接近前面推导出来的理论值φi。

根据转向梯形机构的各项参数，在运动学分析软件中建立转向梯形的虚拟样机模型。仿真模型主要通过构件、标识点、约束、驱动和力等来创建。模型简化后包括两个转向节臂和转向横拉杆。添加一个1°/s的旋转驱动，用来模拟转向运动。转向梯形机构的虚拟样机模型如图4所示。

图4 转向梯形机构的虚拟样机模型

图5是优化前的原始转向梯形机构转弯过程中，车轮内外转角关系和理论转角关系曲线对比图。由图可知，对于初始的转向梯形结构，转弯角度逐渐增大时，内轮的实际转角与理论转角之间的偏差也在逐渐变大。

从图6误差曲线可知，理论转角与实际转角的误差最大值达到1.972°。为提高转向梯形机构的转向性能，可以对该机构进行优化设计。

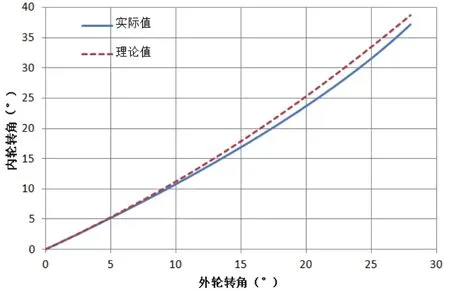
图5 优化前车轮内外侧转角关系

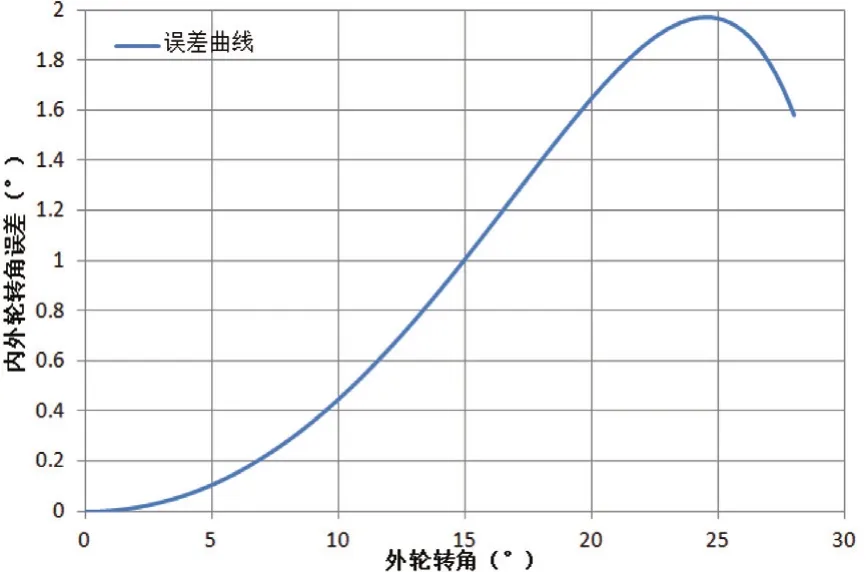
图6 误差曲线

三、转向梯形机构的优化

在运动学分析的基础上，对转向梯形机构进行优化，使其最大限度的逼近理想的阿克曼转向特性，从而提高整车的转向性能。

优化设计的目标就是要保证在实际转向过程中，内外轮转角关系尽量逼近阿克曼转向特性，即在转向过程中，实际内轮转角φi’与理想内轮转角φi的偏差尽可能的小。从而使转向轻便并有效减小轮胎的磨损。根据优化设计的原理，给出了优化目标函数为：

此外，还需要对转向节臂长m及梯形底角β的取值范围设置合理的约束。转向梯形机构必须满足几个条件：mmin≤ m ≤ mmax；β-βmin≥ 0。

根据转向梯形机构设计经验，转向节臂的最小值和最大值取mmin=0.11K、mmax=0.15K，梯形底角最小值取βmin=65°。

为方便分析，将图4中标记点1处的横纵坐标参数化作为优化变量，等价于将转向节臂长m以及梯形底角β作为优化变量。优化变量初始值为：x1=-1805，y1=-563。

使用多学科多目标优化软件对转向梯形机构进行优化。该软件将数字技术、推理技术及设计探索技术有效地融合，并把大量需要人工完成的工作由软件实现自动化处理。使用该软件提供的设计工具，进行从零部件到系统各层级的性能设计和质量设计，可以高效且科学地完成日益复杂和高难度的产品设计任务。最重要的是，在设计阶段保证了产品的可靠性和稳健性。

采用全局探索法进行优化，该方法适应性强，只评价设计点，无须计算任何函数的梯度，因此目标函数可以是多峰性、非线性、非连续、不可微函数。而且能求解全局最优解，避免了集中在局部区域的搜索。优化过程如图7所示。

图7 优化过程

优化结果：x1=-1785，y1=-544。此时，梯形底角β=67.53°，转向节臂长m=588.69mm。（注：优化前梯形底角β=70°，转向节臂m=599.16mm）优化前后车轮内外转角关系和理论转角关系曲线对比如图8所示。优化前后误差曲线对比如图9所示。

从图8和图9可以看出，优化后的梯形机构更能逼近理论转向特性，实际值与理想值能够很好的吻合，最大转角误差从原模型的1.972°减小到0.941°，从而更好地提高转向性能，使转向轻便并减小了轮胎磨损和侧滑。

图8　优化前后内外侧转角关系对比

图9　优化前后误差曲线对比

四、结语

转向梯形机构的设计直接影响着矿用汽车转向系统性能。本文综合应用运动学及结构优化的方法对矿用汽车转向机构进行结构分析和设计研究。

首先通过转向梯形机构运动学分析。以阿克曼转角公式为理论依据，运用运动学分析对转向梯形机构进行了运动学仿真，分析了内外转向车轮之间的转角关系以及实际值与理论值之间的偏差，为转向梯形机构的优化设计提供了理论基础。接着选取合理的优化目标函数，建立了转向梯形机构的优化数学模型。对转向梯形机构进行了优化，使其更加符合阿克曼转向原理，结果表明，优化后的梯形机构更能逼近理论转向特性，最大转角误差从原模型的1.972°减小到0.941°，从而更好地提高了整车转向性能，减小了轮胎磨损和侧滑。本文的研究实现了对矿用汽车转向性能的评价，为矿用汽车设计提供了理论参考。