Arnold活塞环径向压力分布函数的研究

张 钊，赵高晖，王新华 ，李传磊，邵国森

(上海理工大学 机械工程学院，上海 200093)

Arnold活塞环径向压力分布函数的研究

张 钊，赵高晖，王新华 ，李传磊，邵国森

(上海理工大学 机械工程学院，上海 200093)

基于现代活塞环设计方法，研究了Arnold 径向压力分布函数表达式的理论依据，在此基础上提出了一种非仅由余弦函数构成的活塞环径向压力分布函数表达式，分析了该表达式的特性及优点，并用Matlab软件的仿真结果验证了函数与Arnold表达式的关系。结果表明，Arnold表达式可看作非仅由余弦函数的一个特例，非仅由余弦函数表达式形式上更为简洁普遍，其系数仅是压比p(π)/pm和平均压力pm的函数，更适合于活塞环的设计生产。

活塞环；径向压力分布；函数； 数值模拟；仿真验证

活塞环是内燃机中关键零件之一, 具有密封、润滑、导热和定位的作用[1-2]。为使活塞环装入气缸后以适当的径向压力分布作用于缸壁[3]，现代活塞环设计时会按照发动机类型与用途,首先选择较佳的径向压力分布函数,然后计算出符合该压力分布的环的自由形状,按此形状确定靠模凸轮和环模,加工出所需的活塞环形状。因此,径向压力分布函数是活塞环设计的基础和依据[4]。

从径向压力分布形式看，活塞环有3种情况：压力均匀分布的等压环、开口处压力大于平均压力的高点环，以及开口处压力低于平均压力的低点环。在高速发动机中,常用高点环以便抑制环的颤振、提高密封性能[5]。二冲程气口扫气的发动机则常采用低点环[6]。从函数的构成看，活塞环的径向压力分布函数都可由余弦函数构成和非仅由余弦函数构成[7]。本文在分析著名的Arnold径向压力分布函数式基础上，研究非仅由余弦函数构成的通用函数式，以期得到工作性能良好、且便于生产的活塞环。

1 Arnold径向压力函数的研究

理想的活塞环自由状态型线是对称于x轴的，即活塞环径向压力分布函数p(θ)应为偶函数，如图1所示。仅为余弦函数的活塞环径向压力分布函数表达式为

(1)

式中，pm为活塞环的平均压力；cn为函数系数;θ为径向压角。

上式的主要缺点有：对高点环，开口处为压力的极大值, 对抑制环的颤振不利；当压比p(π)/pm较大时，(p(θ)/pm)min之值会太小；k值必须较大,使极值点过多，且k增大时不能显著改进压力分布函数的特性[8]。因此，为得到性能较佳的活塞环，在德国、日本以及我国常应用形式如式(2)的Arnold径向压力表达式[9-11]。

图1 环受径向力作用

(2)

式(2)可从下面的分析和理论推导中得到。

由文献[12]可知，当曲率半径与径向厚度之比r/t很大(活塞环的r/t>10)时, 可仅考虑弯矩的作用，即有

(3)

式中，ρ为活塞环自由状态时的曲率半径；r为气缸半径；M为弯矩；E为材料的弹性模数；J为惯性矩。

对等压环，b点截面上的总弯矩M为

(4)

将式(4)代入式(3)可得

(5)

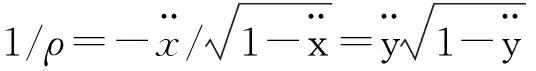
(6)

对于式(6)，由于k值很小, 可用sin[k(α+sinα)]≈k(α+sinα)和cos[k(α+sinα)]≈1的近似关系，经积分得到活塞环的自由状态型线为

(7)

在径向压力非等压时, 式(4)变为

(8)

对式(8) 进行二次求导得

(9)

将式(3)代入式(9)，整理得

(10)

通过1/ρ=(x′y″-y′x″)/(x′2+y′2)3/2和式(7)、式(10)，可得下式

p(α)=p{1+k[(α2sin2α)/2+2(cosα+cos2α)]}

(11)

式(11)是从等压环的自由状态型线式(7)导出，在导出式(7)时用过近似关系, 故p(α)并不完全等于p。在式(11)中，引入两个参数n和l替代式(11)中的1和k，就是式(2)的Arnold活塞环径向压力分布函数式。由此可见，式(2)中的n、l含义不甚明确，且带有相当人为的选择性。

2 非仅由余弦函数表达式的研究

作为活塞环的径向压力分布函数，除余弦函数外，尚有多种偶函数形式[14-15]，如θ2n、sin2nθ、(θsinθ)n(n通常为正整数)等。通过优化组合，可得到相对简单的一种形式[16]

p(θ)=(pm/cm)(1+α2θ2+c1cosθ+c2cos2θ)

(12)

式(12)的主要优点有：压力分布变化比较平缓，即dp/dθ变化小；引入单调上升偶函数θ2后，p(θ)在0～π范围内只有一个极值点，从而使极值点将减少；对于高点环，在θ=π处p(θ)为最大值，而非极大值，这将有利于抑制环振；函数表达式简单，有利于在生产中实施[9]。

活塞环仅在径向压力作用下受力平衡, 即

c2cos2θ)cosθdθ=0

求解可知

c1/a2=4

(13)

cm=1+π2a2/3

(14)

在θ=π时，式(12)可整理为

求解可知

a2>0

(16)

由式(15)和式(16) 得

(17)

由上述分析可知，式(12)中的4个参数cm、c1、c2和a2不可任意选取，式(17)限制了c2/a2的选择范围。一般在式(17)允许范围内选定较佳的c2/a2后，按发动机的要求选取p(π)/pm，然后由式(13)～式(15)得出a2、c2、cm、c1的值，这样径向压力分布曲线就完全确定了。

p(θ)的极值点，由dp(θ)/dθ=0求解，即

(18)

解得

(19)

由式(18)和式(19)可知，p(θ)的极值点是θ=0处，不是θ=π处。对于高点环，径向压力的极小值点θmin仅取决于c2/a2。

3 与Arnold函数式的比较

将sin2θ=(1-cos2θ)/2和cos2θ(1+cos2θ)/2代入式(2)中，可得

(20)

n+(5/4+π2/6)l=n+2.895l=1

(21)

比较式(20)和式(12)可知，式(20)中的cos2θ的系数与θ2的系数之比为3/2，所以Arnold式仅是式(20)的一个特例，其中n和l的关系可由式(21)得到。

由式(19)可计算出取不同c2/a2值时，高点环的(p(π)/pm)min极值点对应的θmin值。pmin=0取不同c2/a2时，θmin和p(π)/pm的部分计算结果见表1。图2是利用Matlab软件模拟式(12)的部分压力分布线图[17]，计算时的平均压力pm=20 MPa。由图线可看出，与Arnold活塞环径向压力分布函数式相比, 本文提出的通用函数式, 较好地涵盖了Arnold式，实际生产中可按需要在更大范围中选择合适的径向压力表达式系数。

表1 pmin时式(12)的特性值

图2 活塞环径向压力为非仅余函数时的压力分布图

4 结束语

(1) Arnold函数式与仅有余弦函数组成的径向压力分布函数式比较，具有极点少、压力变化较平缓，p(π)/pm仅为最大(或最小值)、函数形式简单等优点，但式中参数n、l含义不明，不利于在生产中应用；(2) 利用θ2、θsinθ、sin2θ等非余弦函数进行线性组合，也可得到较为理想的活塞环径向压力函数表达式；(3) 由理论推导和数值模拟结果可验证，文中式(12)既概括了Arnold函数式，又形式简单等优点；0<θ<π时，极值点明确；θ=π时，dp(θ)/dθ≠0，对抑制环的颤振有利。而且式中的系数与p(π)/pm和pm联系密切，更便于实际应用。

[1] БЯ根茨布尔克.活塞环理论[M].谢仲群,译.北京:机械工业出版社,1986.

[2] 长沙铁道学院.内燃机构造与原理[M].北京:中国铁道出版社,1981．

[3] Semenyuk N F, Novikov I I. Calculation of the parameters of contact between piston ring and cylinder[J].Chemical and Petroleum Engineering,2007,23(10): 492-494.

[4] 孙贞义.活塞环压力分布函数的建立与自由状态的计算方法[J]．山东内燃机通讯，2011，15 (2)：6-14．

[5] 黄志云.内燃机活塞环性能研究[D].武汉:华中科技大学,2012.

[6] Nakashima K,Nakano Y,Ishihara S.Behavior of piston rings passing over cylinder ports in two-stroke cycle engines[J]. Journal of Mechanical Science andTechnology,2010,24(1):227-230.

[7] 赵高晖,罗君,左成宝.一种活塞环径向压力分布函数的研究[J].上海理工大学学报,2006,28(4):367-369．

[8] 王伯年,赵高晖.活塞环径向压力分布特性及其在余弦函数表达式上的应用[J].内燃机学报,2000，7 (4):325-332．

[9] 赵高晖,李小兰.一种新型活塞环径向压力分布函数[J].上海理工大学学报,2009,31(3):261-262.

[10] Ji Young K,Jee Woon K,Myung Rae C. Friction characteristics of piston ring pack with consideration of mixed lubrication: Parametric investigation[J]. KSME International Journal，2012,16(4):468-475.

[11] T Ortjohann DIT, Voncken DI A P J. Piston ring dynamics simulation based on FEA software[J]. MTZ Worldwide,2008,69(12):36-41.

[12] 罗迎社,柴维斯. 材料力学[M].北京：高等教育出版社,2013.

[13] 徐森林,纪永强,金亚东. 微分几何[M].合肥：中国科学技术大学出版社，2013.

[14] 赵高晖,王伯年.活塞环压力分布非仅为余弦函数表达式的研究[J].上海机械学院学报,1994,16(1):1-9.

[15] 苏颖颖,王伯年.活塞环径向压力分布函数分析[J].上海理工大学学报,1999,21(1):47-50.

[16] 高保东,黄友胜,李小兰,等.活塞环径向压力分布函数的分析[J]. 上海工程技术大学学报，2007,21(4):315-317.

[17] 周建兴.Matlab从入门到精通[M].北京:人民邮电出版社,2012.

Research and Numerical Simulation of Distribution Function for Arnold Piston Ring Radial Pressure

ZHANG Zhao ，ZHAO Gaohui，WANG Xinhua，LI Chuanlei，SHAO Guosen

(School of Mechanical Engineering ，University of Shanghai for Science and Technology, Shanghai 200093, China)

An non-cosine function expression of the radial pressure distribution on the piston ring was discussed based on the modern designing theory of piston ring and the research of Arnold radial pressure distribution function, its characteristics were analyzed, and the function was compared with the Arnold function expression of the radial pressure distribution making use of the simulate results on Matlab software. The compare result proves the latter is just a special case of the former, which is simpler and more general, and the coefficient in which is only the function ofp(π)/pmandpm.The distribution function suggested is propitious to designing and produced of piston rings.

piston rings；radial pressure distribution；function；numerical simulation；emulation proof

2016- 03- 06

张钊(1992-),男，硕士研究生。研究方向：现代设计在机械设计中的应用。赵高晖(1960-),男，副教授。研究方向：机械设计与理论，CAD/CAE。

10.16180/j.cnki.issn1007-7820.2017.01.027

TK413.33

A

1007-7820(2017)01-097-04