基于动态几何软件的模型教学—以《直线与平面垂直的判定》的教学为例
湖北大学数学与统计学学院(430062) 张素婷
西南大学数学与统计学院(400715) 邓伍丹
基于动态几何软件的模型教学—以《直线与平面垂直的判定》的教学为例
湖北大学数学与统计学学院(430062) 张素婷
西南大学数学与统计学院(400715) 邓伍丹
1 引入
DGS是动态几何软件(Dynamic Geometer Software)的简称,目前使用较广的有几何画板、超级画板等等,这类几何软件为学习者提供了几何探究的开放性台.本文围绕DGS技术,以《直线与平面垂直的判定定理》[1]一课为例,探讨如何将传统的模型教学与DGS技术灵活结合,以减轻学习者认知过程的负担.
《普通高中数学课程标准 (实验)》(以下简称《标准》)指出,通过直观感知,操作确认,归纳出直线平面垂直的判定定理[2],故教学的重点为通过直观演示来探究和理解直线与平面垂直的判定定理.传统的做法是演示实物模型,实物演示固然生动形象,但难免有局限性,如材料工具的不足;难以进行复杂的空间形式变换;个案的演示难以呈现同类事物的数学本质;难以避免偶然误差.这些不足恰好可以由DGS技术来弥补.将实物模型借助DGS技术抽象为几何模型,是形象思维向抽象思维过渡的过程,也是学生在认识事物时从感性认识到理性认识的发展,体现了DGS技术环境中几何教学从几何到技术再到几何的发展过程,是一种促进概念理解和思维发展的过程[3].下面将对“直线与平面垂直的判定”的教学设计中如何直观构建定理来进行探讨.
2 传统模型教学中学生可能会碰到的困难
让学生通过折纸活动来探究直线与平面垂直的判定定理是困难的.皮亚杰说:知识、认识来源于主体和客体之间的交互——活动.很多教师在处理“折纸实验”时并不能清楚认识折纸的目的,未能挖掘其蕴含的深层次数学思维[4].一位教师曾这样指导学生折纸:要让三角形纸片稳当地站立在桌子上.这样的处理虽然有意避开肉眼难以判断线面垂直的不足,但是却忽略了在偏差允许范围内,即使折痕不垂直桌面,也能让三角形纸片立在桌面上,的确有脱离线面垂直的主题之嫌,实际上“折纸实验”应关注的焦点不在于钻牛角尖折痕是否垂直桌面,而在于启发学生为何这样折能让折痕垂直桌面,让学生解释折纸方法的理由.然而在学生还未接触线面垂直的判定定理之前,学生并不能解释其理由,因此在未曾揭开直线与平面垂直的判定定理的面纱之前,让学生通过折纸活动探究发现该定理是不容易的.
3 帮助学生突破难点的策略
在这节课的设计中,许多优质课均借助各式各样的生活中的实物模型来辅助理解,解释说理,但对于模型的使用有时流于表面,不能深层次挖掘模型中所蕴含的数学道理,这无异于买椟还珠.另一方面,实物模型过于形象化,有时难以把实际问题抽象化,这或多或少会阻碍学生对数学本质的认识,这时如果能把实物模型借助DGS技术转化为抽象模型,就会帮助学生真正透过现象看到数学本质.
探究发现判定定理的策略
正如前文所分析,让学生在未尝理解折纸实验的意图之前,通过折纸实验来探究发现定理是不容易的,仅仅折出三角形纸片的一条高就能揭示出线面垂直的定理显然不切实际.因此折纸实验用来探究定理操作性较弱,而用于操作认证该定理较适宜.
模型教学最关键的是选取合适的模型,模型越简单直观越能达到事半功倍的效果.实物演示可采取传统的做法,用一本书来操作演示.此外,笔者还借助几何画板设计了长方体模型,在保证一条侧棱垂直于底面的一条棱、两条平行的棱、两条相交的棱这三种情况下,让长方体“动”起来,观察其倾斜情况.在长方体模型这种常见的立体模型中得到了线面垂直的判定定理,实物模型和几何画板相辅相成,既形象具体,又回归了数学本质,此时由学生之口讲出判定定理已是水到渠成.
4 教学过程设计
据前面所分析,结合执教经验及思考,辅之对优质课教学设计的反思,笔者采用问题链形式,设计了探究定理的教学过程.
模型融合DGS,发现归纳定理
活动1教师演示,学生观察
(1)如图1,将一本书合上,倾斜置于桌面,书脊垂直于书的下底边,即AB⊥BC,此时可视为书脊所在的直线垂直于桌面所在平面内的一条直线,书脊一定垂直于桌面吗?
(2)如图2,将这本书按照(1)中摆放,在桌面内另取一条平行于书的下底边的直线,即AB⊥BC,AB⊥DE,可视为书脊所在的直线垂直于桌面内的两条平行的直线,书脊一定垂直于桌面吗?
(3)如图3,将这本书一分为二均匀翻开,使书的两条下底边与桌面完全接触,即AB⊥BC,AB⊥BD,此时可视为书脊所在的直线垂直于桌面内两条相交的直线,书脊一定垂直于桌面吗?
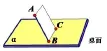
图1

图3
【设计意图】引入这个实物模型用于引导学生发现判定定理,通俗易懂,易于操作,且与前面引入部分前后呼应,实现了一例多用反复强化的作用.有人曾质疑,这个模型完全可以用一张A4纸来替代,其实不然,因为纸张有张力,即使不垂直折纸也能让纸张整体立在桌面上,但用书本来做这个实验就能巧妙地避开这个问题.
几何画板演示1长方体模型
(1)在几何画板中画出一个长方体,保证一条侧棱垂直于底面的一条棱,如图4,AA1⊥A1B1,点击“变换”按钮,观察侧棱是否仍然垂直于底面?
(2)保证一条侧棱垂直于底面的两条平行的棱,如图5,AA1⊥A1B1,AA1⊥C1D1,点击“变换”按钮,观察侧棱是否仍然垂直于底面?
(3)保证一条侧棱垂直于底面两条相交的棱,如图6,AA1⊥A1B1,AA1⊥A1D1,点击“变换”按钮,观察侧棱是否仍然垂直于底面?

图4

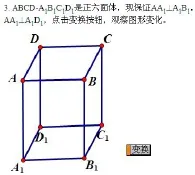
图6
【设计意图】这个环节是整个教学设计中最关键之处,在已有书本的实物演示之后,再引入几何画板动态演示,并非画蛇添足,实际上这两个演示过程实质是相同的,只是后者将实物模型抽象为典型的长方体模型,再次对定理的两个关键条件“双垂直”和“相交”进行理解和确认,一目了然,是形(实形物体)—型(数学模型)—质(数学本质)的自然过渡,这也是学习空间几何元素的关系的重要方法之一.用好这种方法对空间观念的形成、几何概念的把握都十分有效,这实际上是抽象概念与实际事物间的一种桥梁.
【归纳】线不在多,相交则灵.
【反思】探究式学习的基本方式之一就是在观察中发现规律,并进行归纳总结[5].在定理的探究过程中,学生通过观察实验操作,思维上经历了“直觉—直观—矛盾—思考—猜想—归纳”的过程[6],DGS技术将数学现象更直观地展现,从而清晰明了地直指矛盾,给学生进行数学思考和数学表达扫清障碍,这不是剥夺和削弱学生的基本活动经验,而是更高层次地积累数学活动经验,处理好了直接经验与间接经验之间的关系.
5 教学反思——实物模型结合DGS技术对教学效率的影响
在立体几何的教学中,实物模型不可或缺,它是沟通现实世界与数学本质的实体媒介,然而仅仅停留在媒介上就事论事就是功亏一篑.DGS技术的参与使几何问题具体化、模型化、直观化,对启发学生思维起到了推波助澜的作用.在本节课中,实物模型经历了动态演示过程,再借助几何画板将其抽象为只含有图形和符号的数学模型,极大地发挥了信息技术“动态性、交互性”的优势,不少的难点用信息技术做个动画就解决了[7].当然,若想学生达到事半功倍的学习效果,模型的选择至关重要,既要通俗易懂,又要深入浅出,更要凸显数学本质,这是本节课还可继续再斟酌的课题.
[1]刘绍学.普通高中课程标准实验教科书•数学2必修[M].北京:人民教育出版社(A版),2004.
[2]中华人民共和国教育部制定.普通高中数学课程标准(实验)[S].北京:人民教育出版社,2003
[3]尚晓青等.基于DGS技术环境的教学过程及其实现[J].数学教育学报,2010,19(6):94-97
[4]张曜光.从有效教学看数学教学设计—以人教A版“直线与平面垂直的判定”为例[J].数学通报,2008,47(5):18-21
[5]徐章韬,梅全雄.论基于课堂教学的数学探究性学习[J].数学教育学报,2013,22(6):1-4
[6]宋建辉.刍议高中数学实验教学的几个视角[J].数学通报,2015,54(1):9-13
[7]张景中,彭翕成.深入数学学科的信息技术[J].数学教育学报,2009,18(5):1-7

