初唐的数学与礼学*——以诸家对《礼记·投壶》的注疏为例

朱 一 文

初唐的数学与礼学*
——以诸家对《礼记·投壶》的注疏为例

朱 一 文

传世文献中有两条线索刻画了中国古代礼与数学的密切关系：一条线索是《周礼》所述“六艺”之一为“九数”(即数学)，由此被后世学者逐渐扩展为数学是礼学或儒学的一部分；另一条线索是《左传》所云“王命诸侯，名位不同，礼亦异数”，由此被理解为礼数与政治等级相关，并进而以数学安排之。从孔颖达与甄鸾、李淳风等对《礼记·投壶》的注疏看，两方对同一经文及郑玄注运用了不尽相同的数理解释。具体来说，有计算方式与结果、注疏体例与目的等方面的不同；尤其是前者通过书写计算，而后者使用算筹。基于其他文献中也有类似的情形，两方的差异具有一般性。因此，《周礼》所述更多反映了周代数学与礼学的关系，而后世的发展导致算经数学与儒经数学各自逐渐成为相对独立的体系，并且后者与礼学的关系更为密切；《左传》所云侧重关于政治等级的礼数，而未述其关于礼器尺寸的一面。汉代以降，投壶由礼仪向游戏渐变，出土实物与传世绘画印证了其形制的变化；诸家对相关经文的解释就逐渐偏离了实际，而转为相对纯粹的文本学术探讨。在初唐恢复古礼、注疏儒家、算家经典的历史背景下，数学与礼学的关系实际处于文本与现实的多重张力之中。

数学； 礼学； 投壶；《礼记》； 《五经筭术》

一、引言：关于数学与礼学的两条线索

中国古代，礼与数学有密切的关系。传世经典中有两条线索可以用来识别两者的联系：一方面，传本《周礼·地官司徒·保氏》记载“九数”是六艺之一，汉代郑玄注表明此九数就是与当时数学相关的九部分*《周礼》云：“保氏掌谏王恶，而养国子以道，乃教之六艺。一曰五礼，二曰六乐，三曰五射，四曰五驭，五曰六书，六曰九数。”郑玄注：“九数，方田、粟米、差分、少广、商功、均输、方程、赢不足、旁要。今有重差、夕桀、句股也。”([汉]郑玄注、[唐]贾公彦疏：《周礼注疏》，[清]阮元校刻：《十三经注疏》上册，北京：中华书局，1980年，第731页)郑玄注的“九数”，其具体内容已不可考，但学术界一般认为它们与汉代成书的《九章筭术》密切相关(参见郭书春汇校：《汇校〈九章筭术〉增补版》，沈阳：辽宁教育出版社、台北：台湾九章出版社，2004年，第480—481页)。。三国时，魏国刘徽注《九章筭术》云：“按周公制礼而有九数，九数之流，则《九章》是矣。”*郭书春汇校：《汇校〈九章筭术〉增补版》，第1页。据此，学界一般认为数学是周代礼制的一部分，进而亦是儒学的一部分*这一观点在学术界有很深的渊源，几乎成为今天的共识。典型的说法来自钱宝琮：“我们以为《九章算术》和许慎《说文解字》相仿，是东汉初年儒学的一部分，与儒家的传统思想有密切关系。”(氏著：《〈九章算术〉及其刘徽注与哲学思想的关系》，李俨、钱宝琮：《李俨钱宝琮科学史全集》第9卷，沈阳：辽宁教育出版社，1998年，第688页)。。另一方面，传本《左传·庄公十八年》云：“王命诸侯，名位不同，礼亦异数。”*[晋]杜预注、[唐]孔颖达等疏：《春秋左传正义》，[清]阮元校刻：《十三经注疏》下册，北京：中华书局，1980年，第1773页。这就是一般认为的“礼数”。近来，阎步克先生认为：“中国礼制自初就显示出了一个重要特征：浓厚的‘数字化’倾向，大量采用数列手段来区分尊卑贵贱，是所谓‘礼数’……礼制的‘数字化’，首先可能跟‘神秘数字’或‘数术’有关……‘数字化’还有一种行政与管理的意义，为精密安排身份、地位、礼遇及其变动，提供了重大便利。”*阎步克：《服周之冕——〈周礼〉六冕礼制的兴衰变异》，北京：中华书局，2009年，第113—114页。笔者同意阎先生的看法，认为礼数与数学的紧密联系是肯定的，但我们必须拓展“中国古代数学”的内涵，从而进一步分析两者的复杂关系。阎先生进而论证经学家注释经典之时，为了安排礼数需解“不定方程”，即用到数学。

二、诸家对于《礼记·投壶》的不同注解

投壶是中国古代的一种礼仪与游戏，至迟在春秋时代便已产生，为射礼转变而来*《左传·昭公十二年》：“晋侯以齐侯宴，中行穆子相，投壶。”孔颖达等疏：“凡宴不射，即为投壶。”([晋]杜预注、[唐]孔颖达等疏：《春秋左传正义》，前揭书，第2062页)郑玄注《礼记》云：“投壶，射之类也。”([汉]郑玄注、[唐]孔颖达等疏：《礼记正义》，前揭书，第1665页)。从时代背景看，投壶的产生反映出春秋时期礼崩乐坏与文武分途的趋势*参见揣静：《中国古代投壶游戏研究》，陕西师范大学硕士学位论文，2010年，第5—8页。。大体而言，早期投壶礼仪成分更多，越往后则其游戏性越高。传本《礼记》第四十与《大戴礼记》第七十八都是专门的《投壶》篇章。《礼记》经文对于投壶的形制与尺寸有一段论述，即：“壶颈修七寸，腹修五寸，口径二寸半，容斗五升……”*[汉]郑玄注、[唐]孔颖达等疏：《礼记正义》，前揭书，第1666页。《大戴礼记》则云：“壶脰修七寸，口径二寸半，壶高尺二寸，受斗五升，壶腹修五寸。”与《礼记》基本一致。([清]王聘珍撰、王文锦点校：《大戴礼记解诂》，北京：中华书局，1983年，第244页)这即说壶的形状分成上下两个圆柱体：上部分壶颈高7寸，直径2.5寸(二寸半)；下部分壶腹高5寸，容积1斗5升(见图1)。《礼记》经文实际没有直接给出壶腹的直径。因此，汉代大儒郑玄(127—200)注云：

修，长也。腹容斗五升，三分益一，则为二斗，得圜囷之象，积三百二十四寸也。以腹修五寸约之，所得。求其圜周，圜周二尺七寸有奇。是为腹径九寸有余也……*[汉]郑玄注、[唐]孔颖达等疏：《礼记正义》，前揭书，第1666页。

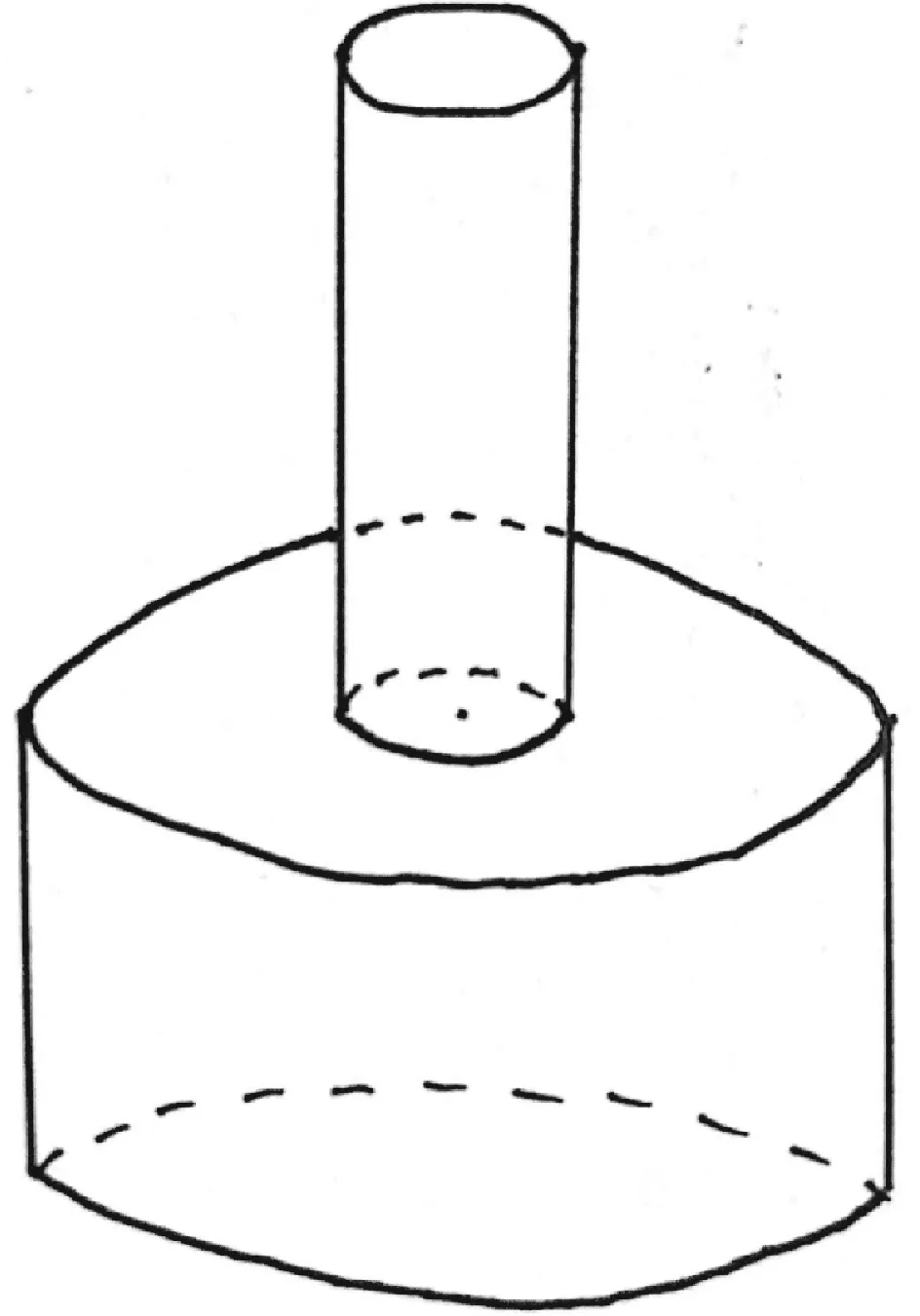
图1 投壶示意图

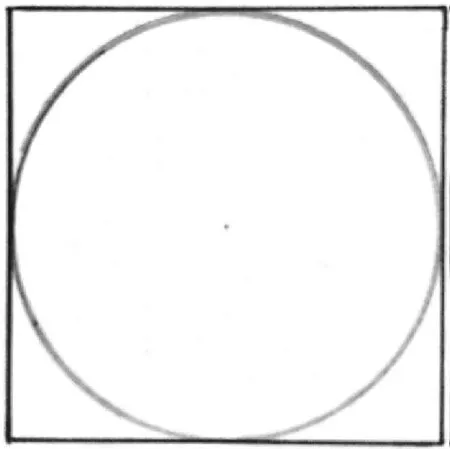
图2 圆与外接方图

(一) 孔颖达等注疏

在初唐注疏《五经》的活动中，《礼记》名列其中*初唐的《五经》指《毛诗》《尚书》《礼记》《周易》《春秋左传》五部儒家经典。。孔颖达等在《礼记正义》中对此段郑玄注给出了详尽的解释，笔者按其内容分成六段，开头以甲、乙、丙、丁、戊、己标识，逐一说明*下面的六段引文，据[汉]郑玄注、[唐]孔颖达等疏：《礼记正义》，前揭书，第1666—1667页；并参考李学勤主编：《十三经注疏·礼记正义》第3册，北京：北京大学出版社，1999年，第1574页。：

甲)正义曰：“腹容斗五升，三分益一，则为二斗”者，既称“腹容斗五升”，又云“三分益一”者，以斗五升其数难计，故加三分益一为二斗，从整数计之。

甲段孔颖达等注疏郑玄“三分益一”。孔氏等以1斗5升难以计算，故而加上1/3，得到整数2斗。

乙)云“得圜囷之象，积三百二十四寸也”者，以筭法方一寸，高十六寸二分为一升，则一斗之积方一寸，高一百六十二寸也。二斗之积为三百二十四寸也。于此壶之圜囷之中，凡有三百二十四寸也。

丙)云“以腹修五寸约之，所得”者，腹之上下高五寸，共有三百二十四寸。今且以壶底一寸约之，即于三百二十四寸之中，五分之一，得六十四寸八分也。是腹修五寸约之所得之数也。

丙段中，孔颖达等通过壶腹的体积324(立方)寸、高5寸来求壶底圆的直径。孔氏等认为以324(立方)寸除以5寸，得到64寸8分。实际上，这个值既可以看作底面积，即64.8(平方)寸；也可以看作是高1寸、底64.8(平方)寸的圆柱体体积(即1/5的壶腹体积)，即64.8(立方)寸。在孔氏等之后的注疏中，我们可以看到：在计算面积时，此数值取面积的意义；在计算体积时，此数值取体积的意义。

丁)云“求其圜周，圜周二尺七寸有奇”者，壶底一重既有六十四寸八分，以圜求方，须三分加一。六十四寸八分，分为三分，则一分有二十一寸六分。并前六十四寸八分*依据计算及上下文，阮元刻本误“六十四寸八分”为“六十六寸八分”，李学勤主编《礼记正义》简体标点本从阮元之误，今正之。参见李学勤主编：《十三经注疏·礼记正义》第3册，第1574页。，得八十六寸四分也*依据计算及上下文，阮元刻本误“八十六寸四分”为“八十六寸八分”，李学勤主编《礼记正义》简体标点本正之，今从之。参见李学勤主编：《十三经注疏·礼记正义》第3册，第1574页。。即是壶底一重方积之数也。今将八十六寸开方积之，九九八十一，则为方九寸强也。一面有九寸强，四面凡有三十六寸强。今以方求圜，四分去一，有二十七寸强，是壶圜周二尺七寸有强。故云“圜周二尺七寸有奇”也。

丁段，孔颖达等求解圆周2尺7寸有奇。孔氏等先求壶底圆的外接正方形面积，按照3:4的关系(取π=3，则圆面积：方面积=3:4，见图2)，需要把圆面积加上其1/3。这样64寸8分+1/3×64寸8分=86寸4分，即是外接正方形面积。开方之后得到9寸强，是外接正方形边长*实际上，这同时是壶底圆的直径，由此可以直接得到圆周2尺7寸强。孔颖达等并未沿此路线计算。。4倍之后，得到36寸强是外接正方形的周长。圆周与方周的比也是3:4(同样取π=3，则圆周长：方周长=3:4，见图2)，则方周减1/4为圆周。这样36寸强-1/4×36寸强=27寸强=2尺7寸强，即圆周。

戊)郑之此计，据二斗之数*“二斗之数”，阮元刻本误为“一斗之数”，李学勤主编《礼记正义》简体标点本正之，今从之。参见李学勤主编：《十三经注疏·礼记正义》第3册，第1574页。。必知然者，壶径九寸，以圜求方，以方九寸计之，凡九九八十一，壶底一重有八十一寸，五重则有五个八十一寸，总为四百五寸。今以方求圜，四分去一，去其一百一寸四分寸之一，余三百三寸四分寸之三。于二斗之积三百二十四寸之内，但容三百三寸四分寸之三*依据计算及上下文，阮元刻本误“三百三寸四分寸之三”为“三百二寸四分寸之三”，李学勤主编《礼记正义》简体标点本从阮元之误，今正之。参见李学勤主编：《十三经注疏·礼记正义》第3册，第1574页。，余有二十寸四分寸之一，不尽。故云“圜周二尺七寸有奇”*按郑玄注，当为“圜周二尺七寸有奇”，阮元刻本误“圜周二十七寸有奇”，李学勤主编《礼记正义》简体标点本正之，今从之。参见李学勤主编：《十三经注疏·礼记正义》第3册，第1574页。，乃得尽也。

戊段中，孔颖达等通过反推的办法验证：郑玄1斗5升取整得2斗，是与壶腹直径9寸多相容的。孔氏等先假设壶腹的直径是9寸，这样壶底圆的外接正方形面积是9寸×9寸=81(平方)寸。这个数值也可以理解成高1寸、底面81(平方)寸的长方体体积(即1/5的壶腹外接长方体)，即81(立方)寸。这样壶腹的外接长方体体积等于5×81(立方)寸=405(立方)寸。取π=3，圆柱体(壶腹)与外接长方体的体积之比等于3:4，后者体积减1/4为前者体积。于是，405(立方)寸-1/4×405(立方)寸=303.75(立方)寸，为壶腹体积。这个数值小于郑玄给出的324(立方)寸。两者之差为324(立方)寸-303.75(立方)寸=20.25(立方)寸。因此，壶腹直径应该比9寸多，壶腹圆周则应该比2尺7寸多。

己)若以斗五升计之，计一十五升之积，有二百四十三寸，则壶之所径唯八寸余也，得容此数。必知然者，凡方八寸开方计之，八八六十四，得六十四寸。壶高五重，则五个六十四寸，总为三百二十寸。以方求圜，四分去一，去八十寸，余有二百四十寸。于一斗五升之积，余有三寸，不尽。是壶径八寸有余，乃得尽也。今检郑之文注之意，以二斗整数计之，不取经文斗五升之义。故云：“圜周二尺七寸有奇。”今筭者以其二尺七寸之圜，必受斗五升之物，数不相会也。云壶体腹之上下各渐减杀，苟欲望合，恐非郑意。

在最后一段——己段中，孔颖达等验证：如果按照《礼记》经文取壶的容积1斗5升计算，其体积相当于243(立方)寸，则其直径只有8寸多，不合郑玄注的圆周2尺7寸有奇。为此，孔氏等采取与戊段中一样的反推办法。先8寸×8寸=64(平方)寸，求得壶底外接正方形面积，此数值也可以视作高1寸、底面积64(平方寸)的长方形体积(即1/5的壶腹外接长方体)。5×64(立方)寸=320(立方)寸，为壶腹外接长方体体积。同样按照3：4的关系，320(立方)寸-1/4×320(立方)寸=240(立方)寸，为壶腹体积。此值比243(立方)寸小3寸。因此，壶腹直径为8寸多。孔氏等最后论道：当时有人想调和2尺7寸和1斗5升，只能说壶腹的尺寸由上至下的尺寸是不同的，不符合郑玄之意。此段孔颖达等实际表明《礼记》经文所载的壶容积1斗5升，与郑玄注给出的壶腹周长2尺7寸是不可调和的，但孔氏等站在郑玄一边。

(二) 甄鸾、李淳风等注释

北周甄鸾编写的《五经筭术》是一部用传统筹算解释经典的数学著作。初唐李淳风等注释十部算经的时候，该书也列入其中*初唐的十部算经指《周髀筭经》《九章筭术》《海岛筭经》《缀术》《孙子筭经》《张丘建筭经》《夏侯阳筭经》《五经筭术》《五曹筭经》《辑古筭经》十部数学著作。北宋元丰年间，《缀术》《夏侯阳筭经》丢失，用《数术记遗》及另一部数学著作(唐人韩延著，被误为《夏侯阳筭经》)替代。。传本《五经筭术》卷下也讨论了《礼记·投壶》的问题。在陈述完经文和郑玄注之后，甄鸾和李淳风等依次给出注解*郭书春校点：《五经算术》，郭书春、刘钝校点：《算经十书》第2册，沈阳：辽宁教育出版社，1998年，第398—399页。：

甄鸾按：斛法一尺六寸二分，上十之，得一千六百二十寸，为一斛。积寸下退一等，得一百六十二寸，为一斗。积寸倍之，得三百二十四寸，为二斗。积寸以腹修五寸约之，得六十四寸八分。乃以十二乘之，得积七百七十七寸六分。又以开方除之，得圆周二十七寸，余四十八寸六分。倍二十七，从方法得五十四。下法一亦从方法，得五十五。以三除二十七寸，得九寸。又以三除不尽四十八寸六分，得一十六寸二分。与法俱上十之，是为壶腹径九寸五百五十分寸之一百六十二。母与子亦可俱半之，为二百七十五分寸之八十一。

臣淳风等谨按：其问宜云：今有壶腹修五寸，容斗五升。三分益一则为二斗，得圆囷之象。问积寸之与周径各几何？曰：积三百二十四寸。周二尺七寸二百七十五分寸之二百四十三。径九寸二百七十五分寸之八十一。

术宜云：置二斗，以斗法乘之，得积寸。以腹修五寸除之。所得，以十二乘之。开方除之，得周数。三约之，即得径数。

李淳风等的注释首先把《礼记》及郑玄注重构为一个数学问题(有“问”有“答”)，接着按照传统数学著作的写法给出算法(即“术”)。虽然李氏等没有给出计算细节，但其“术”与甄鸾的算法一样，并且亦是筹算方法。

三、对《周礼》与《左传》的回应

就此例而言，孔颖达等与甄鸾、李淳风等对于《礼记》及郑玄注的注疏差别很大，反映出两方所运用的数学知识不尽相同。两方相同之处主要在于：都未挑战郑氏将《礼记》经文壶腹容积1斗5升取整为2斗的做法*宋代大儒朱熹曾批评郑玄、孔颖达等人取2斗做计算的做法([宋]朱熹：《仪礼经传通解》，朱杰人、严佐之、刘永翔主编：《朱子全集》第2册，上海：上海古籍出版社、合肥：安徽教育出版社，2002，第255页)，这表明宋代数学、礼学的关系与唐代不尽相同。朱熹的数学知识不是本文的研究重点，因此不做展开，笔者有另文专论之。。这符合唐代“宁道周孔误，讳言服郑非”的学术风气。

两方差别主要体现在：1.计算方式与结果。孔颖达等利用圆方3:4的关系进行圆方之间周长、面积、体积的换算，进而进行简单的估算开方，所得结果为约数*根据笔者先前的研究，初唐学者贾公彦有一种几何开方术，可以取得更精确的数值(参见朱一文：Different cultures of computation in seventh century China from the viewpoint of square root extraction，前揭刊，第 6—18页)。因此，尽管我们知道贾公彦参与了《礼记正义》，但此处他应并未发挥更大的作用(参见[宋]欧阳修、宋祁等：《新唐书》第5册，北京：中华书局，1975年，第1433页)。。甄鸾、李淳风等则直接运用《九章筭术》圆面积公式，并使用筹算开方术得到更精确的数值。2.注疏体例与目的。孔颖达等注疏的主要目的是为了表明郑玄注的正确性，并在戊、己两段中用反推的方法证明郑玄取2斗的正确性：如果取2斗，则壶腹周长2尺7寸多；如果取1.5斗，则壶腹圆直径为8寸多。甄鸾利用筹算开方术得出比郑玄更精确的数值，李淳风等更是重构经文以作为数学问题。因此可以说，与孔颖达等相比，甄、李等人的注释都没有完全遵循郑玄注，而以展现传统筹算数学方法为目的*基于笔者先前的研究，两者的差别还有注疏和算法的结构、对数的认识、对图形的认识、推理的方式等方面。。如果我们考虑到孔颖达与李淳风是互相熟悉，并且作为前辈孔颖达还帮助过李淳风，那么上述差别就更值得重视*贞观十四年(640)，诸儒论历，孔颖达请从李淳风(参见[宋]欧阳修、宋祁等：《新唐书》第2册，第536页)。。两方产生差别的主要原因是：孔颖达等是在做经学研究，而李淳风等是在做算学研究，并且双方的数学知识结构本就有所不同，因此尽管问题相同，但是用到数学自然有别*本文的匿名审稿专家认为：诸家算法不同，还受到经学传统、注疏者知识结构及著作性质的影响。笔者在此表示感谢，并接受建议，认为孔颖达与李淳风熟识，因此他们之间的不同更多是受知识结构与著作性质的影响。。

基于诸家对于《礼记·投壶》的不同注疏，我们可以回应《周礼》与《左传》的记述。一方面，《周礼》记述的九数为其一部分，被郑玄确认为早期数学的九个部分，及刘徽总结这一发展的结果就是《九章筭术》。基于儒经与算经反映的数学知识之差异，《周礼》之后这一礼学与数学关系的脉络具有一定的建构成分。至少在唐初的时候，儒家经典尤其是《礼记》《周礼》《仪礼》所反映的数学是礼学及儒学的一部分，而包括《五经筭术》在内的十部算经所反映的数学与礼学及儒学只有微弱的联系*实际上，甄鸾、李淳风等试图通过《五经筭术》重建《周礼》所建构的数学与礼学或儒学的紧密联系。。换言之，儒经数学与礼学的联系更紧密，算经数学则是相对独立的知识体系。

另一方面，《左传》所述主要是讲与政治相关的礼数，并被阎步克先生等学者衍生到礼数与数学的关系。从投壶的例子我们可以看到，实际上礼数的种类多样，除了与政治、身份等级相关的礼数之外，至少还有礼器尺寸这一礼数。由《五经筭术》而论，该书共38个标题，其中21个标题与天文历法计算有关*《五经筭术》分上下两卷，卷上16问，卷下22问，总计38问。关于天文历法计算的21个标题分别是：1.《尚书》定闰法(卷上第1问)；2. 推日月合宿法(卷上第2问)；3. 求一年定闰法(卷上第3问)；4. 求十九年七闰法(卷上第4问)；5. 推《春秋》鲁僖公五年正月辛亥朔法(卷下第6问)；6. 推积日法(卷下第7问)；7. 求次月朔法(卷下第8问)；8. 推僖公五年正月辛亥朔旦冬至法(卷下第9问)；9. 求次气法(卷下第10问)；10. 推文公元年岁在乙未，闰当在十月下而失在三月法(卷下第11问)； 11. 推文公六年岁在庚子，是岁无闰而置闰法(卷下第12问)；12. 推襄公二十七年岁在乙卯再失闰法(卷下第13问)；13. 推绛县老人生经四百四十五甲子法(卷下第14问)；14. 推文公十一年歲在乙巳，夏正月甲子朔绛县老人生月法(卷下第15问)；15. 推昭公十九年闰十二月后而以闰月为正月，故以正月为二月法(卷下第16问)；16. 推昭公十九年岁在戊寅闰在十二月下法(卷下第17问)；17. 推昭公十九年岁在戊寅月朔法(卷下第18问)；18. 推昭公二十年岁在己卯，月朔法(卷下第19问)；19. 推昭公二十年岁在己卯，正月己丑朔旦冬至，而失云王二月己丑冬至法(卷下第20问)；20. 推哀公十二年岁在戊午应置闰而不置，故书十二月有螽法(卷下第21问)；21. 求十二年闰月法(卷下第22问)。、3个与记数系统有关*这三问分别是：1. 《尚书》《孝经》“兆名”注数越次法(卷上第5问)；2. 《诗·伐檀》毛、郑注不同法(卷上第6问)；3. 《诗·丰年》毛注数越次法(卷上第7问)。、4个与音律有关*这四问分别是：1. 《礼记·月令》黄钟律管法(卷下第1问)；2. 《礼记·礼运》注“始于黄钟、终于南吕”法(卷下第2问)；3. 《礼运》一本注“始于黄钟、终于南事”法(卷下第3问)；4. 《汉书》终于南事算之法(卷下第4问)。、1个来自《周易》*此即卷上第8问“《周易》策數法”。，余下9个可以归为礼数。这9个问题中8个取自《周礼》《礼记》《仪礼》三本著作，1个取自《论语》；其中有2问是关于周代封国领土*即卷上第9问“《论语》千乘之国法”，与卷上第13问“《礼记·王制》国及地法”。、3问是关于度量衡系统*即卷上第14问“求经云‘古者百里当今一百二十里六十步四尺二寸二分’法”，第15问“求郑氏注云‘古者百亩当今一百五十六亩二十五步’依郑计之法”，以及第16问“求郑注云‘古者百里当今一百二十五里’法”。、2问是关于丧礼制度*即卷上第11问“《仪礼·丧服》绖带法”，与第12问“《丧服》制食米溢数法”。、1问是关于车盖尺寸*即卷上第10问“周官车盖法”。、1问关于投壶尺寸(卷下第5问“《礼记》投壶法”，亦即本文所分析)。显而易见，我们必须考虑不同的礼数，以及它们与数学可能的不同关系。这有待将来进一步研究。

四、结语：文本与现实

我们已经从文本的角度分析了孔颖达、甄鸾、李淳风等注疏《礼记·投壶》所展现的不尽相同的数学知识、不同于行政等级的器物尺寸的礼数，并进而以《五经筭术》对礼数进行分类，由此可以初步回应《周礼》《左传》的记述。为了对经典文本所反映出的礼学与数学的复杂关系获得进一步的深入理解，我们必须考察文本产生的历史语境，及其与历史现实的关系。为此，我们将从投壶的历史、初唐注经的语境两方面来分析。

对于投壶的历史，揣静的硕士学位论文《中国古代投壶游戏研究》做过专题研究。笔者概括之并加以阐发。《礼记》记载的投壶是一种礼仪，通常认为是由射礼之一的燕射转化而来*依据《仪礼》，射礼有乡射、燕射、大射三种。郑玄云：“投壶，射之细也。射谓燕射。”([汉]郑玄注、[唐]孔颖达等疏：《礼记正义》，前揭书，第1667页)。在空间、人数等受限或宾主不擅射箭的情况下，投壶便可替代燕射。投壶礼大致有下面八个步骤*揣静：《中国古代投壶游戏研究》，第10—13页。：1. 主人邀请宾客投壶，宾客遵从；2. 主人引导宾客就投壶之宴，并授矢；3. 司射设置壶、中、筭等器物；4. 司射宣布规则，并命令乐工奏《狸首》等乐曲；5. 游戏开始，宾主依次投壶，共投四矢，投中者以筭记分；6. 计算筭筹，多者胜；7. 负者喝罚酒；8. 重复步骤5到7，即进行三局两胜，为胜者庆祝。汉代画像石投壶生动地描述了当时宾主投壶的场景(图3)。

图3 汉代画像石：投壶*中国画像石全集编辑委员会编：《中国画像石全集》第6册，郑州：河南美术出版社，2000年，第86页。

投壶之礼兼具礼仪与游戏的性质，随着时代的变迁，其器物、规则都有所改变。《礼记》所规定的壶尺寸：壶颈长7寸，按周代1寸=2.31cm，约为16.17cm; 壶腹高5寸，约为11.55cm; 口径2.5寸，约为5.78cm; 壶总高12寸，约为27.72cm。郑玄注壶腹直径9寸多，按甄鸾计算约9.29寸，相当于21.47cm。于是壶高与腹径之比约为12:9.29=1.29:1。如果根据《礼记》经文给出的容积1斗5升，按孔颖达等计算(己段)得8寸多，约为18.48cm强。如此壶总高与壶腹径比约为12:8.48=1.41:1，略大于郑玄注。笔者以1.29:1(《礼记》)、1.41:1(郑玄注)两个比例来考察经典及其注疏所载与考古出土实际用壶之间的差异。

1975年山东省莒南县大店莒国殉人墓出土一只春秋时期的陶壶，残高26cm，腹径19.8cm，底径17cm(图4甲)。此壶口沿已残，实际高度应略高于26cm。腹径长度，及壶高与腹径之比(1.31∶1)介于《礼记》与郑玄注之间。1977年河北省平山县三汲寸战国中山王墓出土一只战国时期的铜壶，高58.8 cm，口径24.5 cm(图4乙)。该壶为圆柱体，与《礼记》不符。壶高与直径比(2.4∶1)也远大于《礼记》及郑玄注。由此可见，《礼记》及郑玄注可以部分反映春秋战国时期投壶尺寸情况*据此，在假定《礼记·投壶》能够完全反映现实的前提下，我们可以推断其对应的时代不晚于春秋。。

1969年河南省济源县泗涧沟曾出土一只西汉陶壶，高26.6 cm，颈高13 cm，口径4 cm(图4丙)。其总高与腹径比(目视约为1.8∶1)大于《礼记》及郑玄注。2002年东龙山东汉墓出土了一只绿釉陶投壶，口径4.5 cm，高24 cm(图4丁)，形制接近《礼记》所载。实际上，如果考虑到汉代1尺长度有时比周代短，将厘米转换回汉代尺寸(按1寸=2.135 cm)，那么这两例投壶尺寸很接近《礼记》所载。此外，如果我们考察汉代画像石(图3)中间投壶总高与腹径之比，约在1.2至1.3之间，基本符合《礼记》或郑玄注。因此，我们认为《礼记》经文与郑玄注大致符合汉代投壶的实际情况。

甲：春秋*④⑤ 崔乐泉：《中国古代体育文物图录》，北京：中华书局，2000年，第195,195,195页。乙：战国④丙：西汉⑤丁：东汉*⑦ 转引自王建玲：《投壶——古代寓教于乐的博戏》，《文博》2008年第3期，第77页。戊：初唐⑦

图4 出土投壶

1972年陕西礼泉县唐越王李贞(627—688)幕出土了一件三彩投壶(图4戊)，高35 cm，颈部两侧有双耳。按唐代1寸=3.07 cm换算，此壶高度约为11.4寸，近于《礼记》所载。但是此壶高与腹径比明显过大(目视约为1.8∶1)，而且双耳的出现说明其规则也有所改变，即矢可以投入壶耳*晋代虞檀的《投壶变》与宋代司马光的《投壶新格》均对投壶规则的变化有所论述。。唐代诗人韩愈(768—824)说：“公与宾客朋游饮酒，必极醉，投壶博弈，穷日夜，若乐而不厌者。”*[唐]韩愈：《韩昌黎全集》第2册，北京：燕山出版社，1996年，第754页。这说明投壶作为一种纯粹游戏的角色已经出现。因此，我们可以说孔颖达、甄鸾、李淳风等对于投壶尺寸的注疏、注释是一种文本探讨或曰经学、算学研究，与实际的投壶尺寸、形制只有松散的关系。

阎步克先生从冕服角度论述了其历史发展处于“宗经与复古”和“宗君与实用”的张力之中，并认为唐初有恢复周礼的复古运动*参见阎步克《服周之冕——〈周礼〉六冕礼制的兴衰变异》序言及第10章。。实际上，初唐不仅有孔颖达、长孙无忌等领衔的注解儒经的活动，即《诗经》《尚书》《礼记》《周易》《春秋左传》五部经典的注疏*贞观七年(633)，颜师古考订《五经》([后晋]刘昫等：《旧唐书》第8册，北京：中华书局，1975年，第2594页)。先由孔颖达(574—648)领衔诸儒注疏《五经》，贞观十六年(642)完成(孔颖达在五部经典的序言中都提到贞观十六年完成注疏)。孔颖达去世后，诸儒对注疏仍有争议和讨论，故高宗于显庆元年(651)启动《五经》的再注疏，其结果就是《五经正义》，并于显庆三年(653)颁于天下([后晋]刘昫等：《旧唐书》第1册，第71页；[宋]王溥：《唐会要》第3册，北京：中华书局，1955年，第1405页；[宋]王钦若：《册府元龟》第8册，北京：中华书局，1960年，第7303页)。，而且贾公彦也独立注解《周礼》《仪礼》《礼记》《孝经》《论语》等著作，还有徐彦、杨士勋等人的注经工作；另一方面，唐廷也让李淳风领衔注释十部算经*完成于显庆元年(656)([后晋]刘昫等：《旧唐书》，第2719页)。，《五经筭术》也在其列。因此，我们可以说，这场礼制的复古运动不仅有孔颖达等儒家积极参与，李淳风等算家亦是参与者。故而，就其中展现的初唐礼学与数学的关系而言，不仅处于文本与现实的张力之间，而且处于不同学者群体的张力之间，至于其背后存在的利益、权力等因素则是需要另文深入探讨的议题。

[本文构思直接受到欧盟第七科研框架计划下设欧洲学术委员会支持的大型科研项目“古代世界的数学科学”(Mathematical Sciences in Ancient World，简称SAW，ERC项目号269804)的影响。笔者2016年6月8日在法国巴黎第七大学SAW项目会议、11月19日在中山大学哲学系“经典与解释”讲习会曾报告本文，两次报告的点评人BéatriceL'Haridon、刘伟先生及与会专家的提问与交流，对完善本文的帮助非常大。匿名审稿专家也对本文提出了建设性意见。在此一并表示感谢！]

【责任编辑：杨海文；责任校对：杨海文，赵洪艳】

2016—11—01

国家社会科学基金青年项目“儒家经典注疏中天算文献的整理与研究”(16CZS012)

朱一文，中山大学哲学系暨逻辑与认知研究所(广州510275)。

10.13471/j.cnki.jsysusse.2017.02.015