优化BP神经网络在手写体数字识别中的性能研究

王俊杰

（北京工业大学 北京100124）

优化BP神经网络在手写体数字识别中的性能研究

王俊杰

（北京工业大学 北京100124）

为了提高基于BP神经网络的手写体数字识别分类器的准确率与训练速度，针对基于BP神经网络的手写体数字识别分类器，从代价函数、权值初始化、正则方法消除过拟合几个方面对BP神经网络算法进行了改进。并使用MNIST数据集对分类器进行训练、验证、测试等实验。实验表明，改进后的手写体数字识别分类器的性能得到了优化。

神经网络；BP算法；数字识别；分类器

神经网络具有大规模并行处理、分布式信息存储以及良好的自组织自学习能力等特点。因此神经网络被称为有史以来发明的最美丽的编程范式之一。在传统的编程中，我们告诉计算机做什么，怎么做，将大问题分成很多小问题逐一解决。但是使用神经网络，我们不需要告诉计算机该怎么做，它会自己从观测到的数据中获悉，自己找出问题的解决办法。在这其中，BP神经网络算法应用最为广泛[1]，但是在实际应用该算法的时候发现该算法也存在很多的不足之处，训练速度慢，网络训练失败可能性大，训练结果局部收敛等[2-5]。文中通过改进型的BP算法，提高学习速率，改善神经网络的学习性能，并用改进的BP神经网络来识别MNIST数据集，结果显示识别效果显著提升。

1 BP神经网络基本原理以及改进

BP神经网络能够进行误差反向传播，通常与诸如梯度下降法等最优化方法进行结合使用，这个方法计算出网络中的权重对于损失函数的梯度，将该梯度反馈给最优化方法，用最优化方法求得最小值，然后进行权重的更新。BP神经网络算法是一种有监督的训练方法，且激活函数为非线性可导的[6-8]。

1.1 使用交叉熵代价函数代替常用的方差代价函数

神经网络作为一个分类器模型应当有一个衡量分类结果的评判标准，以此来评判预测和实际结果之间的吻合程度，这个标准就被称为损失函数[9-10]。并不是所有函数都能作为损失函数的，损失函数需要满足两个条件：首先，需要满足非负性，因为我们的目标是要最小化损失函数。其次，我们的最终目标是，当真实输出a与期望输出y越接近时，损失函数的函数值能越小。

方差代价函数：

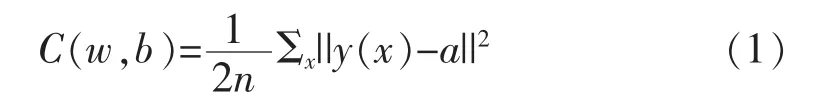
通过公式推导，可得权值w和偏向b关于方差代价函数的更新公式：

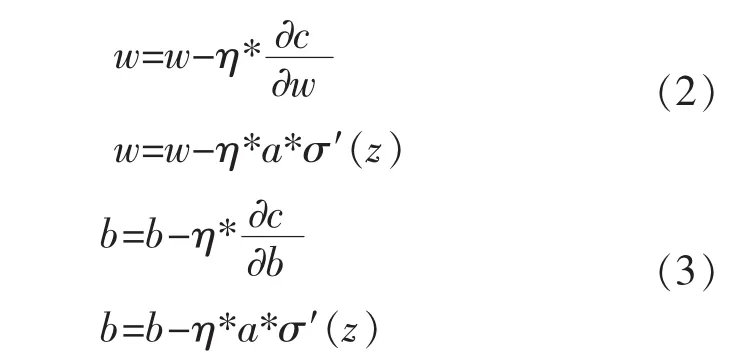
显然，权值w和偏向b的更新取决于σ′（z）。

交叉熵代价函数：

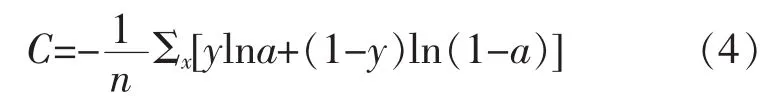
通过公式推导，得权值w和偏向b关于交叉熵代价函数的更新公式：

显然，权值w和偏向b的更新与σ′（z）没有关系，不在受到σ′（z）的影响，只与σ（z）-y有关，这样一来，误差大的时候会加快学习速度。

1.2 使用正则化方法消除过拟合

神经网络与传统的统计中的线性分类器相比，拥有强大的拟合能力，但是往往容易造成过拟合现象。在神经网络分类器训练过程中，过拟合是这样一种情况：一个模型在训练数据上能够获得非常好的拟合效果，但是在训练数据以外的数据集上拟合数据就没有那么好的效果。此时我们就叫这个模型出现了过拟合的现象。过拟合现象的出现的主要原因是进行训练模型的数据中存在噪音或者训练数据非常的少。

文中消除过拟合的方法是一种使权重衰减的方法，简单来说就是在代价函数后加一个正则项：

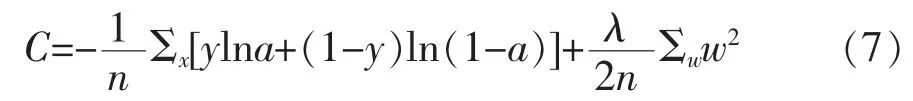
通过推导求得权值w的更新公式：

w的系数是一个小于1的数。这样会使得权值w得到衰减，不至于过大，因为权值过大会使得网络复杂度变大，局部的噪音也会对结果产生比较大的影响。所以采用正则化方法对消除过拟合还是会产生比较好的效果。

1.3 对初始权重的优化

一般在网络训练开始之前，需要进行权值w和偏向b的初始化工作。初始权值的选择一般在区间（-1，1）之间，这是因为小随机数可以保证网络不会进入饱和状态，而权值过大则不然[11-13]。而且各权值最好不要相同。这是因为，神经网络训练过程并不受人为控制，所以没有办法得知神经网络的权重变化的具体情况，但是权值如果都相同，会造成所有的神经元计算出相同的结果，然后在反向传播中有一样的梯度结果，因此误差修正的结果也一样，这就意味着构建的神经网络模型的权重没有办法差异化，相当于没有办法进行学习。在实际的场景中，通常会把初始权值设定为尽可能小的数，并且正负数量尽量相等[14-15]。这样，初始化的时候权重都是不相等的很小的随机数，然后迭代过程中不会再出现结果一致的情况。标准正态分布恰好满足上面的条件，所以初始化权值的时候只要使其满足标准正态分布。但是根据激活函数sigmoid函数的图像，越接近0时学习，变化越大，即学习越快。所以初始化值能尽量落在距离0比较近的位置，开始的训练速度就会比较快，对于整个训练过程来说，相当于加快了训练速度。一般在标准正态分布的基础上将结果除以一个输入个数的开平方就能达到这样的效果。

2 分类器设计

2.1 确定输入输出的数据个数

将MNIST中的图像归一化为28×28的数据信息，即输入层的单元个数应该确定为784个。因为输出层为0到9这10个数，所以将输出层设定为10个单元。

2.2 网络结构设计

网络结构设计主要做的工作是确定中间层的层数以及中间节点个数。文中采用3层结构，即只有一层隐含层。至于节点个数，太少预测精度不够，太多的话泛化能力会下降，需要在具体试验中调试确定，通过实验本文采用30个中间单元。

2.3 使用交叉验证的方法进行训练

具体的做法是把数据集分成n份，每次拿出其中的1份做验证，其他n-1份做训练，n次的结果的均值作为对算法精度的估计。

设计的分类器模型如图1所示。

3 在手写体数字识别中的实验

实验采用MNIST数据集，该数据集分为两部分，60 000个手写体训练集图像，和10 000个测试集图像。在文中使用交叉验证的方式，人为地将60 000幅图分为两部分，其中50 000作为训练集，剩下10 000作为交叉验证集。

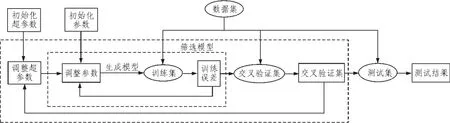
图1 BP神经网络分类器框图

经过试验训练和验证得出以下性能比较：

1）使用交叉熵代价函数与方差代价函数的识别准确率对比

在输入层设定为784个节点，采用3层结构，且中间层节点采用30个节点，每一批量大小为1000，训练30个epochs的条件下，分别使用交叉熵代价函数和方差代价函数进行训练、验证、测试，得到如上的数据结果比较折线图，由上图可以很明显的看到，使用了交叉熵代价函数的识别准确率明显高于使用方差代价函数的识别准确率。

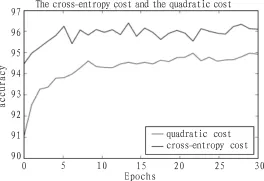
图2 交叉熵代价函数与方差代价函数的准确率对比图

2）使用正则化消除过拟合

在输入层设定为784个节点，采用3层结构，且中间层节点采用30个节点，每一批量大小为100，训练30个epochs的条件下，出现过拟合现象，在上述条件相同的情况下，进行两次试验。如图所示，实验一所使用的代价函数没有进行正则化处理，识别的准确率在80%左右即达到收敛。实验二所使用的代价函数是经过正则化处理的代价函数，识别的准确率在95%左右达到收敛。由此证明，该正则化方式对消除过拟合有效。

3）使用优化的初始权重方法

在输入层设定为784个节点，采用3层结构，且中间层节点采用30个节点，每一批量大小为1 000，训练30个epochs的条件下，分别使用标准正态分布的初始化方式和经过优化的方法，即在标准正态分布的基础上进行了改进的方法，进行初始化，实验数据如上图所示。显然通过新的方法进行初始化后从一开始准确率就比老方法的高，因为两次试验的其他条件相同，证明新的初始化方法的收敛速度要快于老的初始化方法的收敛速度。

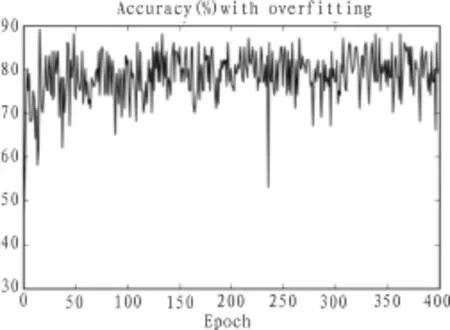
图3 过拟合时的准确率

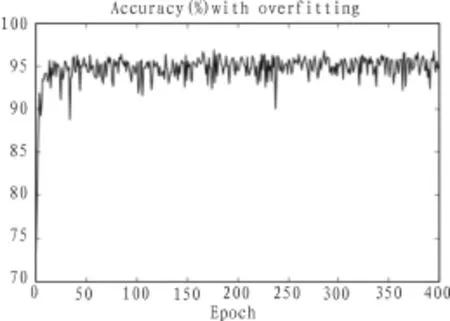
图4 没有过拟合时候的准确率

图5 初始化权重新老方法准确率对比图

4 结 论

从实验结果上看，改进代价函数提高了识别准确率、改进初始化方法加快了训练速度、使用正则化方法一定程度上避免了过拟合。在实验数据有限，超参数设定的尝试次数有限的情况下能得到比较理想的结果，说明优化的网络模型是有效的模型，如果能应用到更大的数据集上，且超参数调试到最好的情况下，预计能有更好的效果。

[1]秦鑫，张昊.基于BP人工神经网络的手写体数字识别[J].计算机与数字工程，2015（2）:223-225.

[2]颜培玉，张国栋.基于人工神经网络的手写体数字识别方法[J].沈阳航空工业学院学报，2008，25（2）:66-69.

[3]王婷，江文辉，肖南峰.基于改进BP神经网络旳数字识别[J].电子设计工程，2011，19（3）：108-112.

[4]刘文杰，吴刚.基于ARM9旳手写体数字识别技术设计与实现[J].计算机与数字工程，2013，41（9）: 1498-1510.

[5]蒋宗礼.人工神经网络导论[M].北京：高等教育出版社，2001.

[6]韩立群.人工神经网络教程[M].北京：北京邮电大学出版社，2006.

[7]袁曾任.人工神经网络及其应用[M].北京：清华大学出版社，1999.

[8]张充，史青苗，苗秀芬，等.基于BP神经网络的手写体数字识别 [J].计算机技术与发展，2008，18（6）：128-130，163.

[9]许宜申，顾济华，陶智，等.基于改进BP神经网络的手写体数字识别[J].通信技术，2011（5）:106-109，118.

[10]樊振宇.BP神经网络模型与学习算法[J].软件导刊，2011（7）:66-68.

[11]张景阳，潘光友.多元线性回归与BP神经网络预测模型对比与运用研究[J].昆明理工大学学报，2013，38（6）:61-67.

[12]刘鲭洁，陈桂明，刘小方，等.BP神经网络权重和阈值初始化方法研究 [J].西南师范大学学报，2010，35（6）：137-141.

[13]刘威，刘尚，周璇.BP神经网络子批量学习方法研究[J].智能系统学报，2016，11（2）:1-7.

[14]刘吆和，陈睿，彭伟，等.一种BP神经网络学习率的优化设计[J].湖北工业大学学报，2007，22（3）: 1-3.

[15]贾立山，谈志明，王知.基于随机参数调整的改进返向传播学习算法 [J].同济大学学报，2011，39（5）：751-757.

Research on performance optimization of BP neural network in handwritten numeral recognition

WANG Jun-jie
（Beijing University of Technology，Beijing 100124，China）

In order to improve the accuracy and training speed of handwritten numeral recognition classifier based on BP neural network，for handwritten numeral recognition classifier based on BP neural network，We improve the algorithm from the following aspects，such as cost function、initialization of weights、regularization method.And we use MNIST data set classifier to train，validate，and test.Experiments show that the handwritten digit recognition classifier improved performance has been optimized.

neural network；BP algorithm；digit recognition；classifier

TN919.82

：A

：1674－6236（2017）06-0027-04

2016-03-29稿件编号：201603390

王俊杰 （1988—），男，山西忻州人，硕士研究生。研究方向：嵌入式与物联网技术。