基于MCL与Chameleon的混合聚类算法

杨连群，刘树发，温晋英，刘功申

（1.天津市滨海新区公安局 天津300450；2.天津市公安局 天津300020；3.上海交通大学 上海200240）

基于MCL与Chameleon的混合聚类算法

杨连群1，刘树发2，温晋英1，刘功申3

（1.天津市滨海新区公安局 天津300450；2.天津市公安局 天津300020；3.上海交通大学 上海200240）

马尔科夫聚类算法（Markov Cluster Algorithm，MCL）是一种快速且可扩展的无监督图聚类算法，Chameleon是一种新的层次聚类算法。但MCL由于过拟合会产生很多小聚类，Chameleon由于时间复杂度为O（N2）不利于处理大规模数据集。针对这两个问题，提出了一种基于MCL与Chameleon相结合的混合聚类算法。该算法第一阶段采用MCL算法对原始数据进行初步聚类，第二阶段利用GPU加速的Chameleon算法将第一阶段产生的小聚类进行归并，从而得到质量更高的聚类。实验表明，与传统的MCL算法和MCL与KNN的混合聚类算法，提出的方法聚类质量更好、计算速度更快。

MCL；Chameleon；聚类算法；图分割算法

聚类分析是探测数据分析的关键步骤，在许多领域都得到了较为成功的应用，如数据分析[1]、Web文档分类[2]、异常检测[3]等。图聚类算法是聚类分析中研究较为广泛的一个分支，目前已有很多关于图聚类的算法被提出，比如谱聚类算法[4-5]，多层聚类算法（METIS）[6-7]等。但在实际运用中仍然有很多不足之处，如：1）谱聚类算法由于需要计算相似矩阵的特征值和特征向量，导致计算时间太长；2）METIS将图的权重进行均等划分，不适合长尾分布的数据；3）谱聚类算法和METIS都不具备智能识别图类别数目的能力等。因此探讨一种计算时间较快、分割质量高且无需事先规定聚类数目的图分割算法是很有必要的。

较之以上的图聚类算法，MCL算法[8]具有以下优势：1）通过对转移矩阵的反复修改来模拟随机流，更易理解；2）不易被拓扑噪声所影响；3）无需预先了解可能潜在的簇结构。但MCL由于过拟合使得容易产生小聚类，从而影响聚类质量。为解决这一问题，可将得到的小聚类再次进行归并，从而得到更高质量的聚类结果。但现存的聚类算法大多只处理符合某静态模型的簇，忽略了不同簇之间的信息。Chameleon算法[9]克服了这一限制，它是一种采用动态模型的图层次聚类算法，在合并两个簇时既考虑了相对互连度，又考虑了相对近似度，具有能高质量地发现具有不同形状、大小和密度的簇的能力。但Chameleon算法时间复杂度为O（N2）不适用于处理大规模数据集。

综上，文中提出一种将MCL和Chameleon相结合的改进图聚类算法，达到了优势互补的效果。具体做法主要分为两个阶段，第一阶段，使用MCL对原始数据集进行初步聚类的划分，得到互不相连的初始子簇；第二阶段，利用GPU加速的Chameleon算法将初始子簇进行归并。实验表明，所提的方法是有效可行的。

1 MCL聚类算法介绍

一个图通常表示为G=（V，E，W），其中V是节点的集合，E是边的集合，W是边权重。图聚类问题就是把图G划分成k个互不相交的子图G=（V，E，W），i=1，2，…，k。记A是图G的邻接矩阵，M为图G的转移概率矩阵，M（i，j）代表节点vi到节点vj的转移概率，因此矩阵M每列之和为1。定义转移概率矩阵M与邻接矩阵A之间的关系如下：

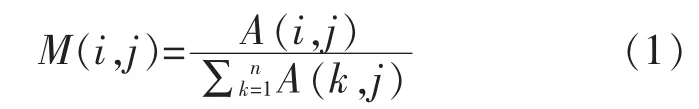
MCL通过反复修改转移概率矩阵来模拟图中节点的转移过程，该过程则是通过扩展（Expansion）操作和膨胀（Inflation）操作来实现的。扩展操作通过扩展参数e来对转移概率矩阵M进行幂乘操作。当扩展参数为e时，该操作如下：

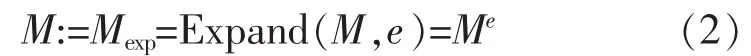
膨胀操作通过膨胀参数r对矩阵M中的每一列进行幂乘操作，再对每一列进行归一化操作。当膨胀参数为r时，该操作如下：

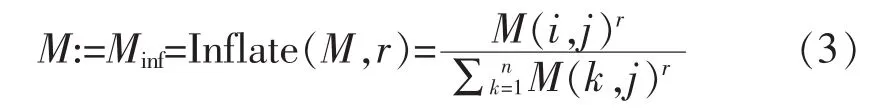
模拟随机流的MCL算法[8]，具体实现步骤如下:

输入：无向图G（有权图或无权图均可），扩展参数e以及膨胀参数r。

1）计算图G的邻接矩阵Α。

2）对每个节点添加自环，即Α:=Α+I，I为对角线元素为1的对角矩阵。

3）利用（1）式，计算转移概率矩阵M。

4）利用（2）式，对M进行扩展操作。

5）利用（3）式，对M进行膨胀操作。

6）重复步骤5），6），直至收敛。判断与上次迭代的矩阵M是否有变化，若无变化，则收敛。

7）根据最后得到的矩阵M进行划分。如图1所示，表示某一无向图的稳定的转移概率矩阵，最后聚类结果应为{1、6、7、10}，{2、3、5}，{4、8、9、11、12}。

图1 矩阵M聚类结果

2 Chameleon算法介绍

Chameleon算法是一种自适应的动态模型算法，实现过程如图2所示，主要分为3个阶段来实现。第一阶段，构造一个k-最近邻居图Gk。第二阶段，将Gk划分成有限个子图，初步得到相对较小的子簇。第三阶段，将第二阶段的初始子簇合并形成最终高质量的簇。以下着重介绍第三阶段的合并准则。

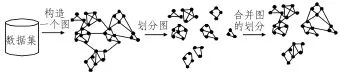
图2 Chameleon算法的主要过程

2.1 相关定义

首先，定义两两簇之间的互连度和近似度，其具体描述如下。

定义1：（相对互连度）簇Ci与簇Cj之间的相对互连度为：

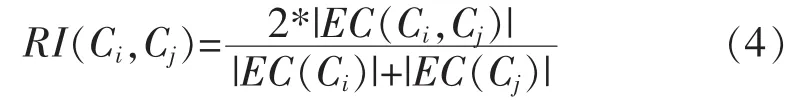
定义2：（相对近似度）簇Ci与簇Cj之间的相对近似度为：

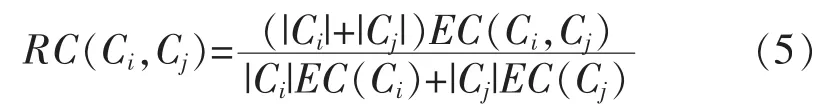
其中，|Ci|表示簇i内数据点的个数；EC（Ci）表示簇Ci内所有边的权重和；EC（Ci，Cj）表示连接两个簇的所有边的权重和。合并方法通过定义如下的相似度函数。

定义3：（相似度函数）相似度函数为相对互连度与相对近似度的乘积，即为：

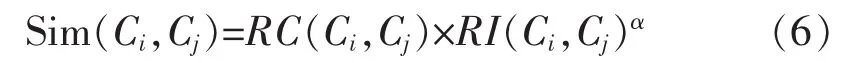
其中，α为用户给定的参数。

2.2 Chameleon算法

1）利用公式（4）和（5），计算两两簇之间的RC和RI，通过函数（6）计算相似度tempMetric。

2）找到最大的tempMetric，若最大的tempMetric超过某一相似度，将簇与此值对应的簇合并。

3）若最大的tempMetric没有超过阈值，则将该簇移除聚簇列表，加入到结果聚簇中。

4）重复步骤3），直到待合并簇类列表最终大小为空，得到K个簇。

3 MCL与Chameleon的混合聚类算法

MCL经过一定步骤的膨胀和扩展之后，会使得节点之间的关系出现偏差。由于偏差不断地扩大，导致处在同一个簇中的边缘点容易被分离出来，从而形成单个的或只有两3个节点的小聚类。为解决这一问题，将MCL产生的小聚类作为Chameleon算法的初始子簇，将每一个子簇看成是一个对象，并寻求一个最终聚类，使簇内部连接紧密，而簇外部连接稀疏。另外，考虑到Chameleon算法的时间复杂度为O（N2），为适用海量数据处理，利用GPU的高并行执行能力，将数据中个两两计算转换为GPU线程块中个线程执行Chameleon算法计算。CPU时间复杂度为O（N2），而GPU只取决于耗时最长的线程时间，且GPU采用分而治之的思想，先单一GPU计算当前模块数据，最后汇总得到结果，再分配下一个计算数据。综上所述，文中采用GPU加速提高了计算时间的同时还能有效地节省硬件成本，更高效地完成大规模的数据聚类分析。实现过程图3所示。

综合以上结论，文提出一种MCL与Chameleon的混合聚类算法描述如下。

第一阶段：

输入：图G，转移概率矩阵M（G），膨胀参数r

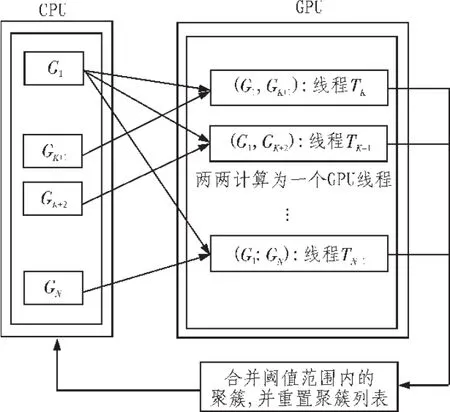
图3 基于GPU加速的Chameleon算法主要实现过程

使用MCL算法

第二阶段：输入第一阶段的簇类信息

使用基于GPU加速的Chameleon聚类算法

输出：最后的聚类结果G={G1，G2，…，GK}

4 算法检验

为检验文中算法的有效性，采用Stanford大型网络数据集[11]中的com_Amazon数据集进行性能测试。Stanford大型网络数据集是关于图形的一个比较全面的数据集，且收集时间较新，因此选用该标准数据集，对算法的验证具有一定的说服力。com_Amazon数据集是由爬虫Amazon网站获得，表示用户与商品之间的购买情况，如果两位用户买过相同的商品，则这两位用户是连接关系。文中实验硬件环境如下：Intel Core i7-4790K CPU@4.00 GHz；主存32 GB；系统平台为Ubuntu14.04 LTS英文版操作系统；软件实施平台为Python 2.7.9（Anaconda 2.2.0）。

4.1 检验标准

DB指标[12-13]是常用的聚类性能度量内部指标，同时使用了簇间距离和簇内离散度，DB的值越小，说明聚类效果越好，反之亦然。模块度指标[14-15]的物理意义为：图中连接两个同簇类的节点的边的比例，减去在同样的图下任意连接这两个节点的边的比例的期望值。若模块度指标Q越接近1，聚类质量越好。

4.2 实验分析

首先，利用MCL算法对com_Amazon数据集进行初始划分，其结果如图4所示，可以看出，随着膨胀参数r的增大，小簇的数量越多，大致呈线性增长，且在总的聚类数目中占了相当大的比例。针对MCL算法所产生的小簇，为证明本文方法的有效性，将本文的方法与文献[8]、[10]进行比较，利用DB指标和模块度指标Q值对聚类质量进行评判，其结果如图5和图6所示。从图5可知，随着聚类数目的增加，DB指标亦逐渐增加，即聚类质量均在下降，其中没经过改进的MCL算法[8]DB指标增加得最快，说明其聚类效果最差；文中算法DB指标最小，这说明文中提出的改进方法效果更好。从图6可知，文中所提出的方法Q值下降速度最慢，这说明聚类质量最好。从图7可以看出，当单一使用CPU计算时，时间呈现指数增长，而GPU时间消耗则较为缓慢，只是随数据增长呈现梯度增加。在效率方面，单个节点的CPU和GPU计算效率两者相当，但是并行处理问题效率远远高于串行处理。算法计算过程中GPU效率比CPU整体效率高出一个数量级。

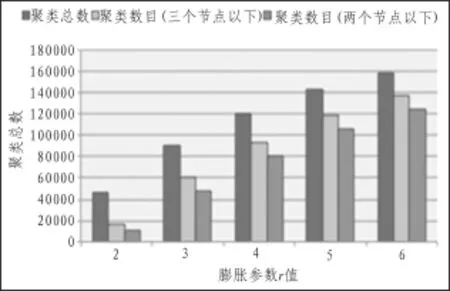
图4 膨胀参数r值对聚类数目的影响

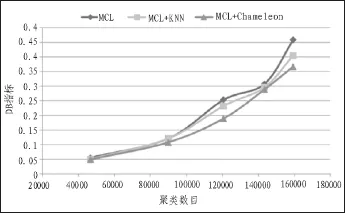
图5 3种聚类算法在com_Amazon数据集的DB指标对比

5 结束语

文中针对MCL算法由于过拟合会产生很多的小簇的不足，并考虑到Chameleon算法的聚类特征，提出一种MCL与Chameleon相结合的混合聚类算法。较之MCL算法和MCL与KNN的混合聚类算法，在产生小聚类时，所提出的算法能得到质量更高的聚类结果，具有较好的实际应用价值。

图6 3种聚类算法在com_Amazon数据集Q值对比

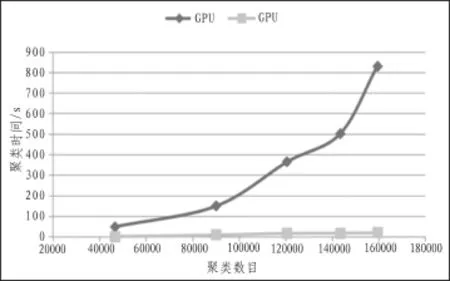
图7 GPU和CPU计算时间对比

[1]ZHANG Xin-yan，SUN Jian-guo.Regression analysis of clustered interval-censored failure time data with informative cluster size [J].Computational StatisticsandDataAnalysis，2010，54（7）：1817-1823.

[2]Manjot K，Navjot K.Web document clustering approaches using K-Means algorithm[J].International Journal of Advanced Research in Computer Science and Software Engineering，2013，3（5）: 861-864.

[3]LIU Bin，XU Guang，XU Qian.Outlier detection data mining oftax based on cluster[J].2012 International Conference on Medical Physics and Biomedical Engineering，2012（33）:1689-1694.

[4]Tseng，Shin-Pin.Normal spectral partition detection fitting for SAC FO-CDMA systems[J].Institute of Electrical and Electronics Engineers，2015,19（12）:2134-2137.

[5]Appalaneni K，Emily C，Anthony F.Single fiber identification with nondestructive excitation-emission spectral cluster analysis[J].Institute of Electr-icaland Electronics Engineers，2014，86（14）:5308-5315.

[6]Zheng L，Wu J，Chen Y，et al.Balanced k-Way partitioning for weighted graphs[J].Journal of Computer Research and Development，2015，52（3）:769-776.

[7]Xu J，Zhong Y，Peng B.Parallel k-Way Partitioning Approach for Large Graphs[J].Advanced Materials Research，2014，912:1309-1312.

[8]Dongen S V，Abreugoodger C.Using MCL to extract clusters from networks[J].Methods in Molecular Biology，2012，804（804）:281-95.

[9]蒋盛益，庞松观，张黎莎.Chameleon算法的改进[J].小型微型计算机系统，2010，31（8）:1643-1646.

[10]牛秦洲，陈艳.基于MCL与KNN的混合聚类算法[J].桂林理工大学学报，2015，35（1）:181-186.

[11]Jure L，Andrej K.Large network dataset collection [DB/OL].（2014-06）http://snap.stanford.edu/data.

[12]周志华.机器学习[M]，北京：清华大学出版社. 2015.

[13]Coelho G P，Barbante C C，Boccato L，et al. Automatic feature selection for BCI:An analysis using the davies-bouldin index and extreme[C]// Intemation Joint Conference on Nevral Networks，Brisbane：2012（20）:1-8.

[14]黄健斌，钟翔，孙鹤立，等.基于相似性模块度最大约束标记传播的网络社团发现算法[J].北京大学学报:自然科学版，2013，49（3）:389-396.

[15]封海岳，薛安荣.基于重叠模块度的社区离群点检测[J].计算机应用与软件，2013，30（5）:7-10.

A hybrid clustering algorithm based on MCL and Chameleon

YANG Lian-qun1，LIU Shu-fa2，WEN Jin-ying1，LIU Gong-shen3
（1.Binhai New Area Public，Tianjin 300450，China；2.Tianjin Public Security Bureau，Tianjin 300020，China；3.Shanghai Jiaotong University，Shanghai 200240，China）

The Markov Cluster Algorithm （MCL）is a fast and scalable unsupervised clustering algorithm for graphs.Chameleon is a new hierarchical clustering algorithm.With the over-fitting of MCL computational process，MCL is prone to producing small clusters.Chameleon clustering algorithm is not suitable for large scale data sets because of the time complexity of O （N2）.In order to solve these two problems，a hybrid clusteringalgorithm based on MCL combined with Chameleon algorithm is proposed. In the first stage，MCL clustering algorithm is used for grouping the data （we call it original partition）. In the second stage，we merge small clusters with the Chameleon clustering algorithm based on GPU acceleration so that the final clusters with higher quality are obtained.Experimental results show that algorithm proposed in this paper has more preferable clustering quality and operation speed than the classical MCL algorithm and hybrid clustering algorithm based on MCL and Chameleon.

MCL；Chameleon；clustering algorithm；graph partitioning algorithm

TN0

：A

：1674－6236（2017）06-0023-04

2016-05-25稿件编号：201605235

国家自然科学基金（61472248）

杨连群（1978—），男，天津人，硕士，高级工程师。研究方向：计算机算法，网络安全等。