含初始缺陷海底管道外压非线性屈曲研究

田 龙，叶天源，彭 超，田润红，谢 天

(1.重庆前卫海洋石油工程设备有限责任公司，重庆 401121；2.中国石油大学(北京) 海洋工程研究院，北京 102249)①

含初始缺陷海底管道外压非线性屈曲研究

田 龙1，叶天源1，彭 超2，田润红2，谢 天2

(1.重庆前卫海洋石油工程设备有限责任公司，重庆 401121；2.中国石油大学(北京) 海洋工程研究院，北京 102249)①

随着海洋油气的开采逐步走向深水，外部静水压力成为深水海底管道的重要环境条件。含初始缺陷海底管道在外部压力的作用下，可能会发生局部屈曲，并沿轴向发生屈曲传播，造成重大损失。为了进一步探究含初始缺陷海底管道在实际工况下受到外压作用时的响应，运用数值模拟方法对海底管道在外压作用下的屈曲特性进行研究。考虑到海底管道材料非线性和几何非线性，通过非线性有限元方法对带初始缺陷管道的压溃力学特性进行了研究；基于Python参数化建模的方法，计算超过1 200个数值模型，对影响带初始缺陷管道屈曲的几何参数和材料参数进行敏感性分析；运用非线性最小二乘法拟合得到极限承载力简化计算公式，并与相关试验数据进行对比，误差小于7%。

海底管道；外压；初始缺陷；屈曲；承载力

随着海洋油气的开发逐步迈向深水、超深水海域，管线运输已经成为海洋油气的主要输送方式[1-2]。在深水、超深水环境下，外部巨大的静水压力逐渐成为海底管道设计中考虑的重要参数。钢管在加工过程中会产生一定的初始椭圆度等几何缺陷；在制造过程中会引起管道材料屈服各向异性，这些因素都会影响管道的结构性能。考虑几何非线性和材料非线性的因素，海底管道在外压作用下很容易发生局部屈曲现象，进而沿轴向发生屈曲传播，造成重大损失。

本文运用Python语言进行参数化建模，建立并计算超过1 200个管道模型，分析了管道在外压作用下的屈曲响应和极限承载力，以及管道径厚比、初始椭圆度、管材屈服应力、材料硬化系数和钢管屈服各向异性对管道极限承载力的影响。基于这些模型的数值模拟结果，拟合出管道外压承载能力简化计算公式，并和已有试验结果进行对比。

1 有限元模型验证

考虑材料的非线性特性，材料的应力、应变关系用Ramberg-Osgood模型[3-4]来描述。

本文中海底管道的材料选取API X52钢，其屈服应力σy=386 MPa，泊松比μ=0.3，弹性模量E=207 GPa，材料硬化系数[5]n=13.6(已有研究表明，该硬化系数可准确地反映钢管在外部压力的响应)。

有限元模型的单元类型选用C3D8R，通过网格敏感性分析确定环向单元数为36，管道径向和轴向单元数分别为6和1。

对于海底管道而言，初始椭圆度是其主要的缺陷形式，为获得真实的管道非线性屈曲响应，在有限元模型中加入初始椭圆度。

采用与Kyriakides分析的海底管道屈曲特性相同的几何和材料参数[6]，可以得到不同径厚比下极限承载力的有限元结果，并将其与Kyriakides等试验结果作对比，如图1所示。

图1 不同径厚比下管道极限承载力有限元仿真结果与试验结果对比

通过对比，验证了非线性有限元模型的适用性和准确性。

2 屈曲理论研究

假设存在轴向一致的外部压力p，对于较长的海底管道，忽略其端部约束条件的影响，可以通过平面假设建立二维模型。由于管道径厚比通常比较大，因此可以通过薄壁环理论来求解管道的变形，运用Sander壳体理论进行分析[7]。管道变形前后截面形状如图2所示。管道截面中任一点的位移如图3所示。

图2 管道变形前后截面形状

图3 管道截面中任一点的位移

假设管道沿轴向的变形是一致的，则其截面上任一点的应变可表示为

(1)

外压作用下结构总势能为

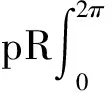
(2)

式中：Nθθ和Mθθ分别为截面剪力和弯矩。

使用变分方法推导得出的平衡方程为

(3)

(4)

考虑到屈曲模态，w和v可表示为

w=acosnθ

(5)

v=bsinnθ

(6)

式中：a和b分别为变形后椭圆的半长轴和半短轴的长度。

将式(5)、(6)代入式(3)、(4)得：

(7)

根据非平凡解，矩阵的行列式为0。因此，得到特征值序列pn为

(8)

实际应用中，ρ远小于1，可忽略，因此1+ρ的值近似为1。对应n=2的最小特征值即为管道的屈曲压力，而且(n=2)是主要屈曲模态，即：

(9)

式中：pc为管道椭圆化模态的屈曲压力；Do为管道的平均直径。

管道经过一定比例放大后的截面如图4所示。管道初始几何缺陷可分为壁厚随角度的不均匀变化和半径随角度的不均匀变化2部分。

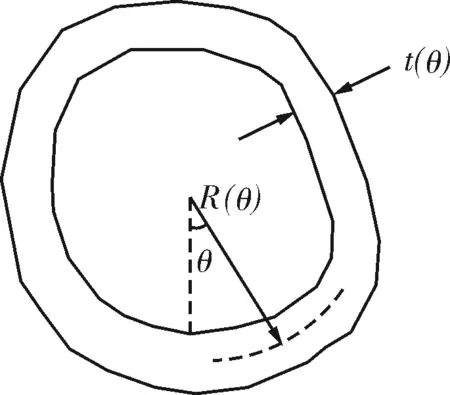
图4 管道截面缺陷示意

引入初始缺陷后，式(3)、(4)则变为

(10)

(11)

(12)

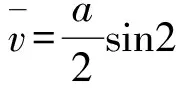
(13)

通过对比可得：

w=Acos2θ

(14)

v=Bsin2θ

(15)

A、B的解由式(16)求得。

(16)

将求得的A和B的解代入式(14)和(15)得：

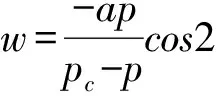
(17)

(18)

将初始屈服发生时的压力作为管道临界屈曲压力的保守上限值，当薄膜应力和弯曲应力叠加到屈服应力σo时，管道开始发生屈服。此时截面弯矩和剪力为

(19)

Nθθ≌-pR

(20)

初始屈服点的应力σo为

(21)

如果将屈服开始的位置与压溃结合起来，式(21)又可表达为

pco-(po+ψpc)pco+popc=0

(22)

式中：po为屈服压力；ψ为参数；Δo为初始椭圆度；Dmax和Dmin分别为管道截面的最大与最小直径。pco为海底管道在外压作用下的极限承载力。

(23)

3 主要影响因素分析

影响海底管道承压能力的主要因素有几何参数和材料参数。几何参数包括径厚比D/t和初始椭圆度Δ0等；材料参数包括管道材料的屈服应力、应变硬化系数n和屈服各向异性S等。模型参数值如表1。

表1 模型参数值

注：X52，X60，X65，X75，X80，X100和X120为钢材等级。

不同径厚比下管道极限承载力有限元仿真与理论计算结果的对比如图5所示。从图5中可以看出，当径厚比D/t≤30时，两者之间的结果相差较大，因此本文主要研究径厚比为12.5～30.0的管道。根据管道设计规范的要求，制造过程中管道初始椭圆度需小于1%，本文取初始椭圆度的研究范围为0.1%～1.0%。

本文使用Python方法[8]调用ABAQUS/CAE反复创建和分析不同参数下的非线性有限元模型。不同的参数组合可得到大量的模型，基本可覆盖大多数实际的管道设计参数。

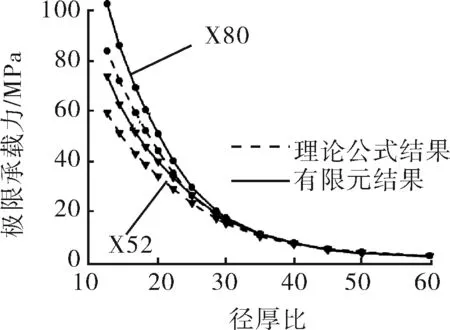
图5 不同径厚比下X80和X52管道极限承载力有限元仿真与理论计算对比曲线

3.1 几何参数的影响

不同径厚比时管道在外压作用下的特征响应曲线如图6所示，图中黑块表示压溃开始的位置。

从图6中可以看出，提高管道径厚比可以明显提高其承压能力。在外压加载的初始阶段，管道所受的外压和截面最大位移基本成线性关系，且径厚比越大，增长速度越快；此后外压的增长速度越来越慢，直至产生最大极限承载力。另外，径厚比越大，外压增长越缓慢。当径厚比较大时，管道发生压溃处的变形也较大。但在D/t≤20时，径厚比的不同对屈曲模态影响有限。

图6 不同径厚比下管道在外压下的特征响应曲线

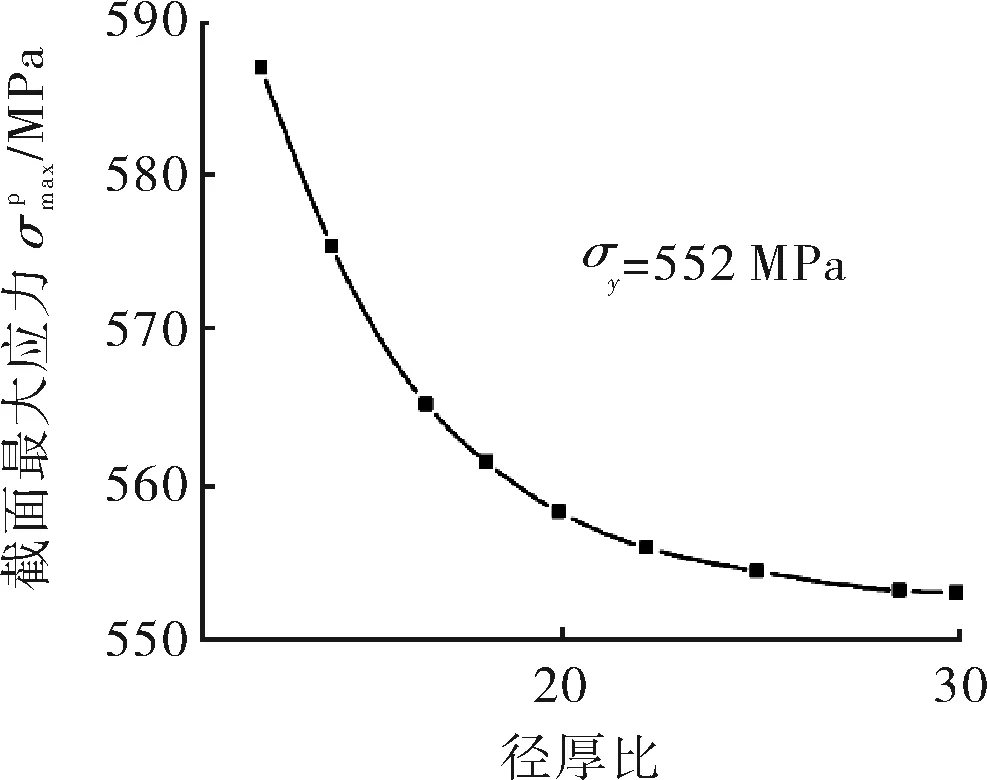
图7 对应极限承载力的截面最大应力与径厚比关系曲线

由图7可知，随着径厚比的增大管道发生压溃时的最大应力逐渐减小，但在所考虑的参数范围内，它们的最大应力均大于材料屈服应力。管道在发生屈曲时处于塑性应力状态，发生的是塑性屈曲。对于径厚比较大的管道，其屈曲形式将发生变化，管道的屈曲模态将不再是典型的压溃形式，而是接近梁的形式。因此，管道可以承受的静水外压存在最大值的原因，对于弹性屈曲而言是因为管道截面弹性失稳，而对于塑性屈曲则主要是因为材料的屈服。

不同椭圆度时管道在外压作用下的特征响应曲线如图8所示。随着初始椭圆度的增加，管道的承压能力逐渐减小，同时管道在发生压溃时的变形愈来愈大。因此，屈曲模态很大程度上会受初始椭圆度的影响。

当初始椭圆度增加至1%时，相应的管道承压能力下降了20%以上。

不同初始椭圆度下管道极限承载力与径厚比关系如图9所示。从图9中可以看出，对于带初始几何缺陷的管道，径厚比对管道极限承载力的影响非常大。当径厚比较小时，随着径厚比的增大管道极限承载力快速减小，径厚比的值从12.5增加到20.0时，管道极限承载力减小了大约60%。另外，初始椭圆度对管道极限承载力的影响会随着径厚比的增大而减弱；对于超薄壁的管道，初始椭圆度对极限承载力的影响可忽略不计。

图8 不同初始椭圆度下管道在外压下的特征响应曲线

3.2 材料参数的影响

不同应变硬化系数下材料的应力应变关系曲线如图10所示。钢材的应力-应变关系受应变硬化系数n的影响比较大。n越大，材料进入屈服以后应变的增加速度越快，这意味着微小的应力变化将产生较大的应变。

图10 不同应变硬化系数下材料的应力-应变关系曲线

不同应变硬化系数时管道在外压下的特征响应曲线如图11所示。

由图11可以看出，应变硬化系数对管道后屈曲路径有比较明显地影响。随着n的增加，管道的承压能力会略有降低，同时发生压溃时的变形也更小。

图11 不同应变硬化系数时管道在外压下的特征响应曲线

不同应变硬化系数时管道极限承载力与径厚比的关系曲线如图12所示。

图12 不同应变硬化系数下管道极限承载力与径厚比关系曲线

由图12可见，当n=6.5时极限承载力最高。不同材料硬化系数下，承压能力的差别在径厚比较小的时候相对较明显，最大的差别约7%；而当D/t>15时，应变硬化系数的改变对管道承压能力几乎没有影响，管道极限承载力受n的影响相对较小。

材料的屈服应力也是深水海底管道设计的重要因素。不同屈服应力时管道在外压下的特征响应曲线如图13所示。

图13 不同屈服应力时管道在外压下的特征响应曲线

从图13中可以看出，响应曲线随着管道的椭圆化变形而开始出现分叉，这是由于随着变形的增加，管道开始出现屈服现象；通过提高屈服应力的值可增强管道的承压能力。

不同屈服应力情况下管道极限承载力随管道径厚比的变化曲线如图14示所示。

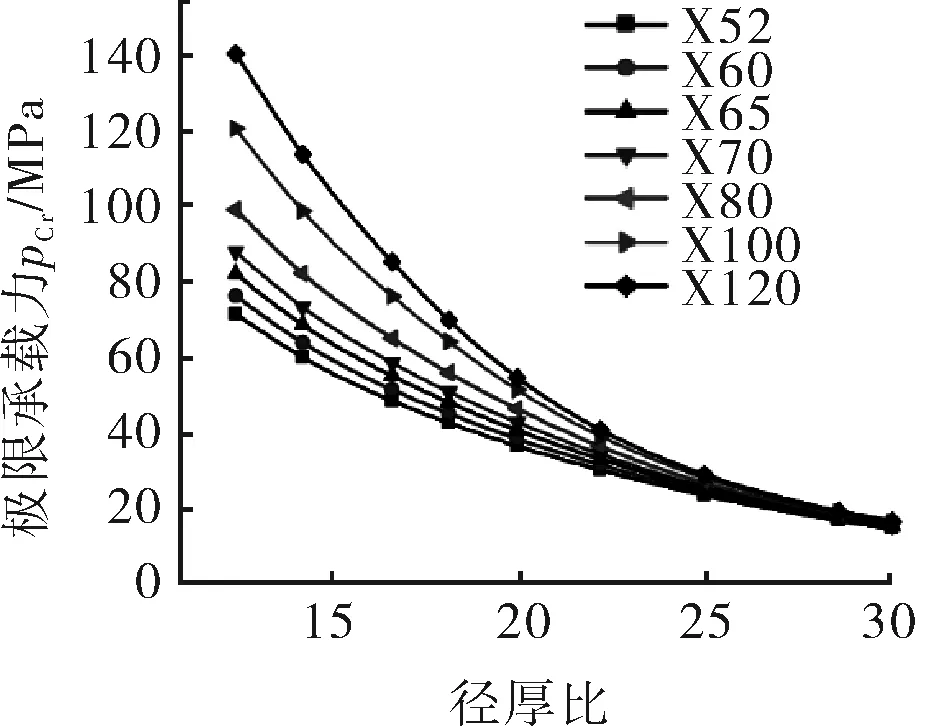
图14 不同屈服应力时管道极限承载力与径厚比对应关系曲线

由图14可见，管道屈服应力σy对管道承压能力的影响程度受径厚比D/t的影响。当屈服应力σy增大时，管道极限承载力随之增大，而且D/t越小，σy对极限承载力的影响就越大，反之，则越小；当径厚比D/t>30时，σy对极限承载力的影响可忽略不计。这是由于径厚比不同所引起的管道屈曲类型的不同。

材料参数中除应变硬化系数和屈服应力之外，材料屈服各向异性对管道承压能力的影响也需要考虑，尤其是对于含有高钢级钢管的极限承载力的影响。管道在冷成型过程中会发生屈服各向异性现象，其程度取决于制造过程[9]。最主要的屈服各向异性形式为轴向和环向屈服应力之间的差别，这种各向异性在屈服函数中通过S来表示。各向异性参数不同时管道极限承载力与径厚比对应关系曲线如图15所示。

图15 各向异性参数不同时管道极限承载力与径厚比对应关系曲线

图15中，管道承压能力通过对应的S=1时的极限承载力进行无量纲化。可以看出，管道极限承载力随着S的增大而增大。同时，当S<1时，管道极限承载力随着径厚比的增加而变大；而当S>1时，管道极限承载力随着径厚比的增加而减小。对于径厚比较小发生塑性屈曲的管道，S对极限承载力的影响较大。根据曲线趋势，对于径厚比较大、发生弹性屈曲的管道，S对极限承载力的影响就比较小。因此，对于深水海底管道而言，屈服各向异性参数是管道设计时必须予以考虑的参数。

管道极限承载力与各向异性参数对应关系曲线如图16所示，无量纲化极限承载力pCr/pCr(S=1)与S成近似比例关系。因此，当考虑各向异性屈服对极限承载力的影响时，屈服压力为

(24)

图16 管道极限承载力与各向异性参数对应关系曲线

4 含初始缺陷管道极限承载力预测公式

从图5可知，屈曲临界载荷的理论公式对于厚壁管道(D/t<30)极限承载力的预测是不够准确的，主要原因是理论公式没有充分考虑到管道材料和几何非线性特性的影响。对于厚壁管道，其主要的失效形式是塑性屈曲和压溃。因此，需要一个简化、精确的公式来弥补理论公式的不足。本文通过参数化建模得到了超过1 200种不同参数组合下的有限元模型，基于这些模型的数值模拟结果可用非线性拟合的方法推得极限承载力的预测公式。

基于理论计算的表达形式，极限承载力可用函数形式来表达，即：

pcr=f(D,t,σy,E,μ,imp)

(25)

式中：imp表示初始几何缺陷。

根据理论公式的表达形式，利用参数化建模数值结果所能得到的极限承载力简化预测式为

(26)

式(26)是基于屈服压力公式，并考虑了初始椭圆度对管道极限承载力的影响。

在SPSS中运用非线性最小二乘法对所得结果进行非线性拟合，获取的参数值如表2所示。表中列出了有限元仿真算得的极限承载力与预测公式结果之间最大误差为7.965%。考虑到管道还会受到其他的材料和几何非线性因素的影响，因此预测公式的误差范围是可以接受的。

表2 参数值

简化预测公式也可以用来研究几何参数与材料参数对完好管道极限承载力的影响，如图17所示。从图17可以看出，通过有限元方法和本文提出的预测公式计算得到的管道极限承载力结果比较吻合。

图17 管道径厚比不同时有限元结果与公式结果对比曲线

简化公式中还需要考虑屈服各向异性参数S对管道极限承载力的影响[10]。当考虑屈服各向异性时，根据屈服各向异性参数对管道极限承载力的影响研究可知，S与极限承载力近似成比例关系。考虑屈服各向异性参数时的简化公式为

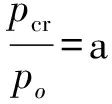
(27)

Yeh和Kyriakides[11]对于带初始缺陷管道在外压下的承压情况做了很多试验方面的研究[6]。将试验中的参数代入公式，所得的极限承载力对比曲线如图18所示(试验中材料的S值为0.877)。

从图18中可以看出，计算结果与试验结果非常相近，最大误差为6.375%。考虑到实际管道壁厚不均匀、材料初始残余应力等因素都会对结果造成影响，因此简化公式的误差范围是可以接受的。图18中用简化公式预测径厚比D/t=39.12的管道时，计算结果与试验结果非常接近，说明简化公式对于径厚比D/t>30的管道也有很好的预测效果。

图18 公式计算结果与试验结果对比曲线

5 结论

1) 径厚比是管道设计中最重要的因素。比较不同径厚比在外压作用下的响应，可以得出管道极限承载力随着径厚比的增加而减小；不同径厚比的管道发生压溃时对应的截面最大应力随着径厚比的增大而减小，径厚比影响着管道的屈曲类型。对于不同初始椭圆度的管道，其承压能力随着初始椭圆度的增加而减小；同时初始椭圆度对管道压溃时的模态也有较大影响；初始椭圆度对管道极限承载力的影响还受径厚比的影响，对于薄壁管道，初始椭圆度的影响相对较小。

2) 材料参数中应变硬化系数对管道承压能力的影响较小，而对管道后屈曲路径有比较明显地影响；当提高屈服应力时可一定程度上提高管道的极限承载力，但其影响程度与径厚比有关。对于管道径厚比较小时，材料屈服各向异性对极限承载力的影响较大；同时，极限承载力与材料屈服各向异性成近似比例关系。

3) 针对深水海底管道，提出了其在外压作用下的极限承载力简化预测公式。与有限元、试验结果比较，简化公式对于绝大部分参数下管道的极限承载力的预测结果非常相近，简化公式与试验结果的误差小于7%。

[1] 李清平.我国海洋深水油气开发面临的挑战[J].中国海上油气，2006，18(2)：130-133.

[2] 刘楚，王佐强，韩长安，等.海底管道事故类型及维修方法综述[J].中国石油和化工标准与质量，2012，23(15)：254-255.

[3] 石永久，王萌，王元清，等.钢框架梁局部屈曲损伤描述材料本构分析[J].应用基础与工程科学学报，2012，22(4)：665-676.

[4] Yong Bai，Ragnar Igland，Torgeir Moan.Tube collapse under combined pressure，tension and bending loads[J].International Conference of Offshore and Polar Engineering，Osaka，1993，3(2)：121-129.

[5] Arjomandi K，Taheri F.A new look at the external pressure capacity of sandwich pipes[J].Marine Structure，2011(24)：23-42.

[6] Yeh M K，Kyriakides.On the collapse of inelastic thick-walled tubes under external pressure[J].ASME Journal of Energy Resources Technology，1986，108(5)：35-47.

[7] Sanders.An Improved First Approximation Theory for Thin Shells[R].NACA reports，1959.

[8] Cojocaru D，Karlsson A M.An object-oriented approach for modeling and simulation of crack growth in cyclically loaded structures[J].Advances in Engineering Software，2008，39(12)：995-1009.

[9] Corona E.Yield anisotropy effects on buckling of circular tubes under bending[J].International Journal of Solids and Structures，2006，43(22)：70-89.

[10] He Tong，Duan Menglan，Chen An.Prediction of the collapse pressure for thick-walled pipes under external pressure[J].Applied Ocean Research，2014，47(8)：199-203.

[11] Kyriakides S，Shaw P K.Inelastic buckling of tubes under cyclic load[J].Journal of Pressure Vessel Technology，1987(109)：169-178.

Buckling Research of Subsea Pipelines with Initial Defects under External Pressure

TIAN Long1，YE Tianyuan1，PENG Chao2，TIAN Runhong2，XIE Tian2

(1.ChongqingQianweiOffshorePetroleumEngineering&EquipmentCo.,Ltd.,Chongqing401121，China； 2.OceanEngineeringResearchInstitute，ChinaUniversityofPetroleum，Beijing102249，China)

With constantly promoting of oil and gas development from shallow water to deep sea，external pressure is a critical loading condition for subsea pipelines.The local buckling may occur for pipelines with initial defect under external pressure.The local buckling may lead to the collapse propagated simultaneously.To further explore the subsea pipeline with initial defect under external pressure being in the actual situation，the characteristic buckling under the numerical simulation methods described herein subsea pipeline which external pressure has been studied.Taking into account non-linear material and geometric nonlinear subsea pipeline，the mechanical properties of crushed paper with initial defect pipeline was studied by nonlinear finite element method，and based on Python parametric numerical modeling method，calculating over 1 200 times，to geometry and material parameters buckling of pipelines with initial defect sensitivity analysis，and the use of non-linear least squares fitting ultimate bearing capacity simplified formula，and finally with relevant experimental data were compared.

subsea pipelines；initial imperfection；external pressure；buckling；pressure capacity

2016-09-22 基金项目：国家重点研发计划“新一代水下生产系统关键力学基础科学的理论研究”(2016YFC0303708)；工信部2013年高技术船舶(海洋装备)科研项目“水下采油树配套工具研发”(工信部联装[2013]41号) 作者简介：田 龙(1989-)，男，重庆人，主要从事水下生产系统设备的研发。

1001-3482(2017)02-0019-08

TE952

A

10.3969/j.issn.1001-3482.2017.02.005