具有脉冲种间偏利关系的Lotka-Volterra系统的动力学行为分析*
李紫君, 李 东
(重庆大学 数学与统计学院,重庆 400030)
具有脉冲种间偏利关系的Lotka-Volterra系统的动力学行为分析*
李紫君, 李 东**
(重庆大学 数学与统计学院,重庆 400030)
对具有偏利关系的Lotka-Volterra种群系统进行研究,首先提出了具有固定时刻脉冲的偏利关系的Lotka-Volterra模型;然后利用周期脉冲微分方程的相关理论,分析了系统的一致持续性,讨论了系统周期解的存在唯一性及其全局吸引性的充分条件;最后通过一个具体实例进行了数值模拟,从而验证了所获得的理论结果的有效性。
偏利关系模型;脉冲;全局吸引性;周期解
种群间的相互关系通常有3种:捕食与被捕食的关系[1-3]、竞争关系[4-7]、互惠关系[8]。偏利关系是指两种群相互作用对一方有利而对另一方没有影响的种群关系。具有这种关系的种群有很多,如地衣、苔藓附在树皮上,从空气中获得水分和养分;喜光的乔本植物为耐阴的灌木提供遮阴条件;一些藤本植物与被缠绕植物之间也有偏离关系。从现有参考文献来看,对偏利作用下种群关系的研究却很少,现有的关于偏利作用种群的研究大多是在种群发展连续没有外界突然灾害干扰的情况下进行的。如文献[9]分析了在连续情况下平衡点的稳定性;文献[10]在文献[9]的基础上进一步对其进行定性分析;文献[11]虽分析了具有固定时刻脉冲收获偏离关系的模型的平衡点的稳定性,却没有对系统的解的全局性进行分析。
在描述种群相互作用的模型中,Lotka-Volterra系统是最经典的模型之一,因此,通过建立起具有脉冲偏利关系的Lotka-Volterra种群系统,分析其一致持续性,给出周期解的存在唯一性及其全局吸引性的充分条件,并给出其实际生物意义。
1 系统模型
两种群相互作用的Lotka-Volterra模型[12]的一般形式如下:
(1)
具有偏利作用下的Lotka-Volterra模型为
(2)
其中x≥0,y≥0,r1>0,r2>0,k1>0,k2>0,a>0.r1,r2分别代表种群x,y的内禀增长率;k1,k2分别代表种群x,y的环境最大容纳量;a>0表示在种群x的环境中,每存在一个种群y的个体,对种群x的作用效应;在竞争作用条件下,种群x受益(偏利),种群y不受影响。
然而,上述传统的Lotka-Volterra偏离共生关系模型是假定种群发展为连续的,但在实际中由于外界的瞬间干扰会使其产生中断,从而也就产生了脉冲。具有固定时刻脉冲收获的偏离关系模型如下:
(3)

引理1[11]设x(t),y(t)T是系统(3)的解,且x(0+)>0,则当0<μ<1,0<ν<1时,对所有的t≥0,有x(t)≥0,y(t)≥0,进一步,若t>0,则x(t)>0,y(t)>0。
因此关于系统(3),易知有以下结论成立:

故由模型的实际意义,只考虑系统(3)的非负解,并称满足条件(x(t),y(t))>0,t≥t0的解u=(x(t),y(t))为式(3)的正解。此处所指的全局性质仅要求对所有的正解成立即可。
2 一致持续性
在一个生态系统中为了保持生态系统的多样性,任何一种生物的种群数量都不允许无限增长或消失的,这就是所谓的种群数量的一致持续性问题,因此先讨论在种群模型中种群数量保持一致持续性的条件。
定理1 当
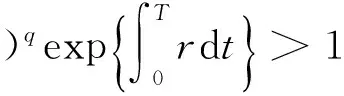
(4)
时,系统(3)是永久持续生存的。
证明 要证明系统(3)的永久性,即证明系统(3)的所有正解有严格正的上界和严格正的下界。
首先证明系统(3)有严格正的下界,为此考虑系统:
(5)
记w(t)为系统(5)的解,u(t)为系统(3)的解,则由脉冲微分方程的比较原理(文献[14]中的定理1.4.4)可知,当t≥t0时,u(t)≥w(t),故只需证明系统(5)的解w(t)有严格正的下界。
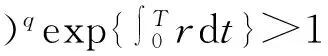
下证其具有正上界,为此首先证明系统(3)中的y(t)是有界的。
由系统(3)可知:
(6)
要考虑系统(6)的有界性,可以先考虑系统:
(7)
其中δ为任意正数。
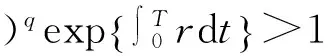
要证明系统(3)的解有正的上界,只需考虑系统
(8)
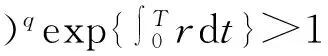
至此关于系统(3)的解的有界性的证明已证完,再结合文献[13]中的定义1.3.2可知,在定理1条件下系统(3)是永久持续生存的。
定理1说明在一定条件下,种群x和种群y的数量会在一个区间范围内波动,但永远不会超出这个区间,这个时候在不发生其他突发情况下,两种群会永久持续生存下去。
3 周期解的存在唯一性及其全局吸引性
对于一个具有一致持续性的生态系统而言,人们最关心的往往是生态系统的渐近性行为,即具有偏利共生关系的两个种群它们将最终以一种什么样的形式共生。周期解是系统的一种特殊解,因此在考虑周期解的性质前先分析系统一般解的全局渐近性行为。首先,引入下面条件:
(F) 假设存在正常数n,β1,β2,使得对于所有t≥0,有

成立。

(i) 如果条件(F)成立,则当t≥t0时下式几乎处处成立:
r′(t)≤
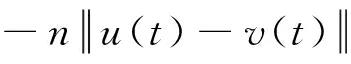
(ii) 如果条件(F)和式(4)成立,则存在常数λ>0,μ>0,使得
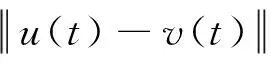

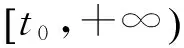
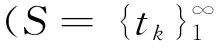



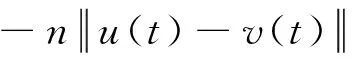
(9)
因此(i)得证。
结论(ii)的证明由于和文献[2]中的定理2.2.2的证明相似,在此不再进行详述。
在定理2条件下,无论两种群的初始状态怎样,但最终种群x和种群y的数量都将会趋于一种发展情况,在这种情况下以一种特殊的关系保持稳定。
在定理2的基础上,结合文献[13]中的定义1.3.3,可得到以下关于周期解存在唯一且全局吸引的推论。
推论1 假设式(4)和条件(F)成立,则系统(3)存在唯一正周期解u0(t)=(x0(t),y0(t)),且u0(t)为全局吸引的。
推论的证明与文献[2]中的定理2.3.1的证明相似,在此不再详述。
下面给出保证系统(3)的正周期解存在唯一且全局吸引的一组容易验证的充分条件。


(10)
则推论1成立。
证明 即证在定理3条件之下,条件(F)和式(4)同时成立即可。
(i) 首先注意到,对i=1,2,式(4)就等价于λi>0;
(ii) 其次,若记C=(cij)是一个2×2矩阵,其元素为
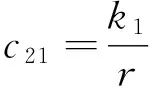
记向量ω=(ω1,ω2),因此可选取δ>0充分小,使得Cω<(1-δ)ω。进一步可得
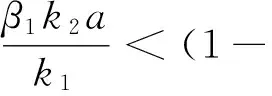


在定理3条件下,无论两种群的初始状态怎样,但最终种群x和种群y的数量都将会趋于一种周期发展情况,以一种周期的形式相互共生存,这种情况在自然界中是普遍存在的。
4 实例及数值模拟
给出一个实例和一些数值模拟以解释验证所获得的主要结果。首先,记

(1-ν
假设两偏利种群x(t),y(t)构成的脉冲种群系统由下面模型描述(T=1,q=1,tk=k∈N+)
(11)
其中x≥0,y≥0,r>0,k1>0,k2>0,a>0.r分别代表种群x,y的内禀增长率;k1,k2分别代表种群x,y的环境最大容纳量;a>0表示在种群x的环境中,每存在一个种群y的个体,对种群x的作用效应;在竞争作用条件下,种群x受益(偏利),种群y不受影响。
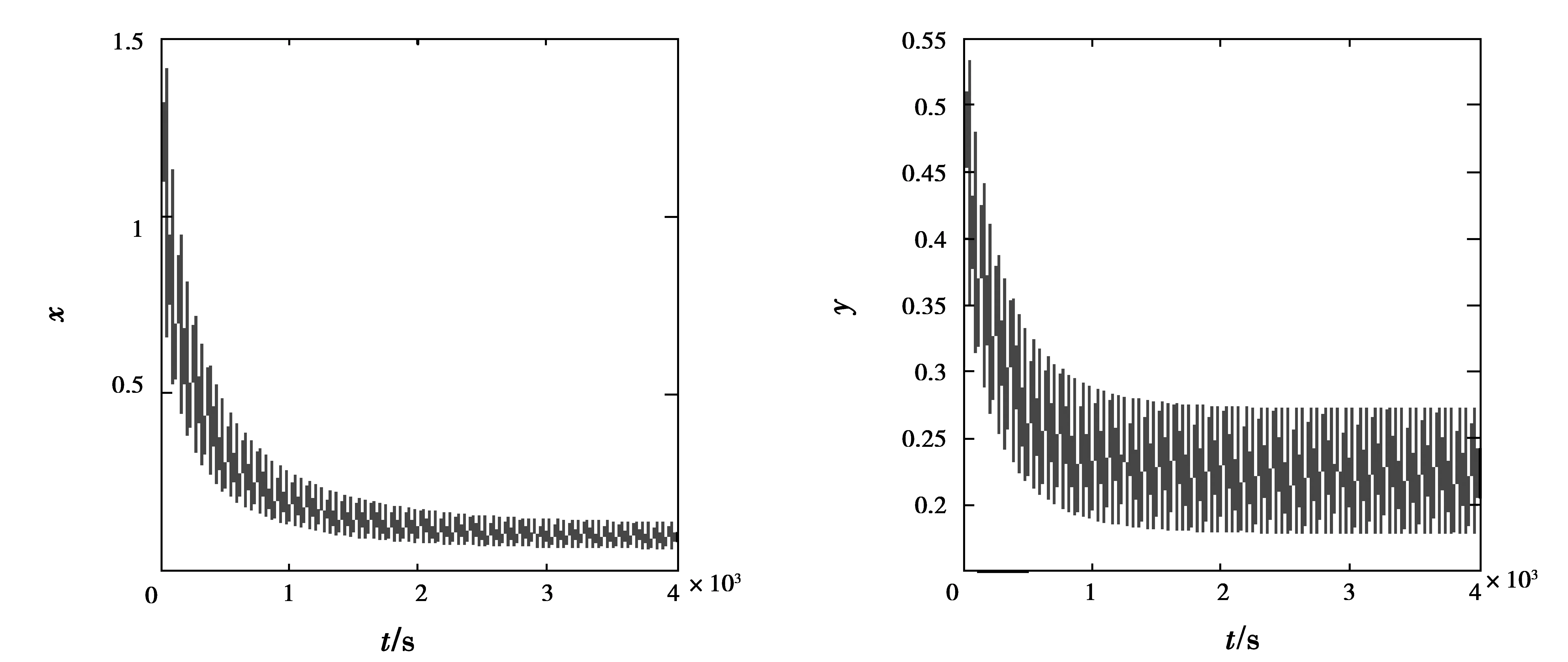
为了简化方程以便于数值模拟的编程,不妨取r=k1=k2=1,脉冲条件可以看作每隔一定时间T=1对种群收获一次的作用,比例系数0 图1 系统状态图(μ=0.73,v=0.81,a=3.06)Fig.1 The two populations of (10) tend to extinction 图2 系统状态图(μ=0.54,v=0.35,a=2.12)Fig.2 The two populations of (10) surviving forever (iii) 如果取μ=0.54,v=0.35,a=0.03,此时由图2的分析可知满足定理1的条件,又max(k2a/r)=0.03<1,可知满足定理3的条件,故此时系统(10)存在唯一的周期解且为全局吸引的。图3为初值是(0.9,0.4)时的周期解的时间序列图。从图3中可以看出两种群的数量呈周期性变化。 图3 周期解的时间序列图(μ=0.54,v=0.35,a=0.031)Fig.3 System(10) has a periodic solution 在实际的生态系统中生物种群之间的许多变化规律都体现出了脉冲效应,比如,在农业生产中对害虫的治理、突如其来的自然灾害如干旱、洪涝、台风等,这些突发性的因素都会给种群的发展造成一定的影响,因而具有脉冲效应的微分系统才更加符合实际需要。重点研究了一种具有固定时刻脉冲收获的种群偏利关系模型。首先给出了系统(3)保持一致持续性所需要满足的条件,接着利用脉冲微分系统的比较原理进一步得到了系统在条件(4)下解的有界性,从而也就得到了系统(3)的一致持续性。其次,在条件(4)和(F)同时成立的情况下给出了种群的渐进性质,为了更易于验证,给出了保证(F)成立的另一组条件,之后又在渐进性质的基础上讨论了系统正周期解的存在唯一性及其全局吸引性,并且在每一个定理的后面都给出了其相应的生物意义。同时,将模型推广为周期系统,亦可得到结论。最后给出了一个具体的实例,并对其进行了数值模拟,验证了所获得的主要结论。 然而在实际的生态系统中,种群的变化率不仅与当前的状态有关,还与过去某一时刻或某一时期的状态有关,因此会有时滞现象的发生。所以,在接下来的工作中,需要通过考虑相应的具有脉冲时滞性的系统来进一步研究种群的发展状况,这样得出来的结果将会更加符合实际。 [1] NIE L F,TENG Z D.Existence and Stability of Periodic Solution of a Predator-prey Model with State-dependent Impulsive Effects[J].Mathematics and Computers in Simulation,2009,79(7):2122-2134 [2] 楚玉.几类脉冲种群竞争系统解的渐近性质[D].西安:陕西师范大学,2013 CHU Y.Asymptotic Properties of Some Impulsive Competition Systems[D].Xi’an:Shaanxi Normal University,2013 [3] ZHANG S W,CHEN L S.A Study of Predator-prey Models with the Beddington-DeAnglis Functional Response and Impulsive Effect[J].Chaos,Solitons and Fractals,2006,27(1):237-248 [4] AHMAD S.On the Nonautonomous Lotka-Volterra Competition Equations[J].Proceedings of the American Mathematical Society,1993(117):199-204 [5] AHMAD S,MONTES D O.Extinction in Nonautonomous T-periodic Competitive Lotka-Volterra Systems[J].Applied Mathematics and Computation,1998,90(2-3):155-166 [6] AHMAD S,LAZER A.Necessary and Sufficient Average Growth in a Lotka-Volterra System[J].Nonlinear Analysis,1998,34:191-228 [7] ZHEN J,HAN M A.The Persistence in a Lotka-Volterra Competition Systems with Impulsive[J].Chaos,Solitons and Fractals,2005,24(4):1105-1117 [8] TONG L,WANG Z A.Asymptotic Nonlinear Stability of Traveling Waves to Conservation Laws Arising from Chemotaxis[J].Journal of Differential Equations,2011,250(3):1310-1333 [9] 祝占法,栗永安,徐芳.具有偏利关系的Lotka-Volterra模型[J].重庆工学院学报(自然科学版),2007,21(10):59-62 ZHU Z F,LI Y A,XU F.Mathematical Analysis on Commensalism Lotaka-VolterraModel of Populations[J].Journal of Chongqing Institute of Technology(Natural Science Edition),2007,21(10):59-62 [10] 孙广才,魏文礼.两种群偏利作用模型的定性分析[J].数学理论与应用,2003,23 (3):65-68 SUN G C,WEI W L.The Qualitative Analysis of Commensal Symbiosis Model of Two Populations[J].Mathematical Theory and Application,2003,23 (3):65-68 [11] 石金喜,窦霁虹,绍彩宏.具有脉冲种间偏利关系的Lotka-Volterra模型的稳定性分析[J].纯粹数学与应用数学,2012,28 (3):357-362 SHI J X,DOU J H,SHAO C H.Analysis of Stability of Commensalisms Lotka-VolterraModelwith Impulsive Effect[J].Pure and Applied Mathematics,2012,28 (3):357-362 [12] 陈兰荪.数学生态学模型及研究方法[M].北京:科学出版社,1988 CHEN L S.Mathematical Ecology Model and Research Method[M].Beijing:Science Press,1988 [13] 张玉娟.脉冲微分方程在种群生态管理数学模型研究中的应用[D].大连:大连理工大学,2004 ZHANG Y J.The Application of Impulsive Differential Equations in Mathematical Modeling of Population Ecology Management[D].Dalian:Dalian University of Techno-logy,2004 [14] LAKSHMI V,BAINOV D D,SIMEONOV P S.Theory of impulsive Diferential Equations[M].Singapore:World-Scientific,1989 [15] DOU J W,CHEN L S,LI K T.A Monotone-iterative Method for Finding Periodic Solutions of an Impulsive Cometion System on Tumor-Normal Cell Interaction[J].Discrete and Continuous Dynamical System-series B,2004,4(3):555-562 责任编辑:田 静 The Dynamical Analysis of Commensalisms Lotka-Volterra Model with Impulsive Effect LI Zi-jun, LI Dong In the study of the commensalisms Lotka-Volterra model, firstly, the Lotka-Volterra model of the partial profit relation with fixed time pulse is established.Then, the relevant theories of differential equations with cycle pulse are used to analyze the existence and uniqueness of the periodic solution and the global attractivity. Finally, we give an example to illustrate the validity of our analysis by the numerical simulation. commensalisms model; impulsive; global attractivity; periodic solution 2016-03-04; 2016-04-05. 国家自然科学基金(11202249);中央高校基本科研业务费专项资金(CQDXWL-2013-002). 李紫君(1991-),女,河南焦作市人,硕士研究生,从事微分方程与动力系统研究. ** 通讯作者:李东(1977-),男,重庆合川人,副教授,博士,从事微分方程与动力系统研究.E-mail:398425146@qq.com. 10.16055/j.issn.1672-058X.2017.0002.012 O193 A 1672-058X(2017)02-0053-07



5 结 论
(College of Mathematics and Statistics, Chongqing University, Chongqing 400030, China)

