一类具有多个偏差变元高阶微分方程反周期解的存在唯一性*

徐建中，周宗福

(1．亳州学院 数学系，安徽 亳州 236800；2．安徽大学 数学科学学院，合肥 230601)

一类具有多个偏差变元高阶微分方程反周期解的存在唯一性*

徐建中1，周宗福2

(1．亳州学院 数学系，安徽 亳州 236800；2．安徽大学 数学科学学院，合肥 230601)

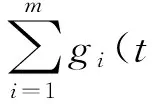
偏差变元；Leray-Schauder度;反周期解

0 引 言

泛函微分方程反周期解问题在细胞神经网络、Hopfield神经网络、流体力学和非线性弹性力学等方面都有着广泛的应用.近年来，有许多学者都在致力于这方面的研究[1-6]，但还很少见到有多个偏离变量的高阶微分方程反周期解存在唯一性的文献.本文利用Leray-Schauder定理，讨论了方程(1)的反周期解的存在和唯一性.这里T>0，n≥2，τi,e∈C(R,R),f∈(Rn,R),gi∈C(R2,R).

x(n)(t)+f(t,x(1)(t),x(2)(t)，…，x(n-1)(t))+

(1)

为了方便研究，作出以下假设：

(H0) 存在非负的常数ci,i=1，2，…，n-l，使得

≤

(H1) 存在非负常数bi,i=1,2,使得

∀t,x1,x2∈R，i=0,1,2,…,m

(H2) 存在T>0，∀t,x∈R，i=0,1,…,m,有

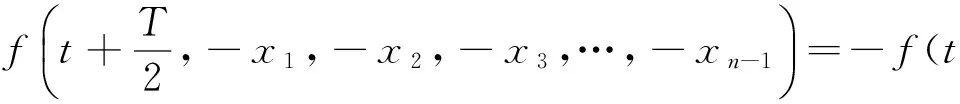
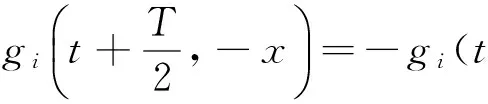
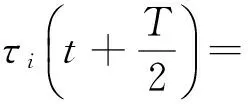
为了应用方便，有以下注记：

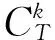
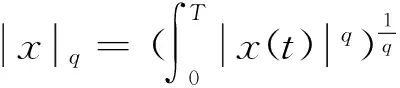
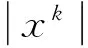
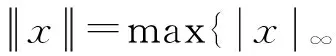
1 引 理

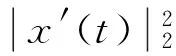
证明 若x1(t)和x2(t)是方程(1)的两个反周期解，令Z(t)=x1(t)-x2(t),则有

τi(t)))-gi(t,x2(t-πi(t)))=0

(2)

又因为Z(t)=x1(t)-x2(t)是R上的反周期函数，则有

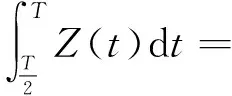
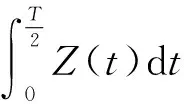
(3)

(4)

可得

(5)

(6)

由式(5)(6)，可得

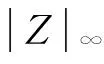
(7)

将式(2)两边同乘以Z(n)(t)，并从0到T上积分，则有

(8)

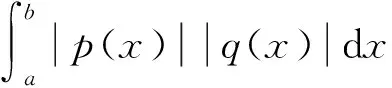
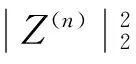
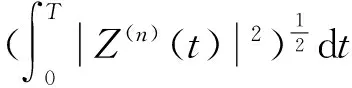
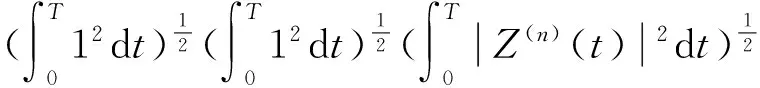
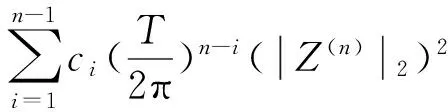
(9)

既然Z(t),Z′(t),Z″(t),…,Z(n)(t)为连续反周期函数，根据假设(H3),式(4)和式(9)，可得

Z(t)≡Z′(t)≡Z″(t)≡…≡Z(n)(t)≡0,∀t∈R

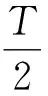
2 主要结果

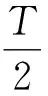
证明 考虑方程(1)的辅助方程：

x(n)(t)=-λf(t,x(1)(t),x(2)(t),…,x(n-1)(t))-

(10)

这里λ∈(0,1],由引理2知方程(1)至多有一个反周期解，接下来只要证明方程(1)至少有一个反周期解即可.为了应用引理3，首先，要证明方程(10)所有可能的反周期解均为有界的.

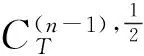
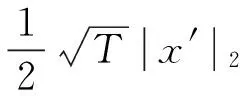
(11)

将方程(10)两边同乘以x(n)(t)并从0到T上积分，根据式(11)(H3),Schwarz不等式和Wirtinger不等式，有

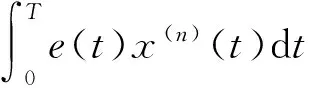
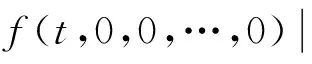
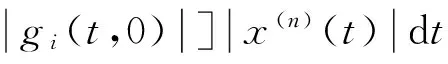
(12)

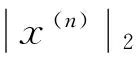
j=1,2,…,n

(13)

既然x(j)(0)=x(j)(T)(j=1,2,…,n),因此存在一个常数ζj∈[0,T],使得x(j)(ζj)=0.

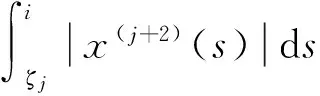
(14)

这里j=0,1,2,…,n-1,t∈[0,T],联立式(11)(13)和式(14)可知，存在一个正的常数D2,使得

即式(10)的所有反周期解x(t)都存在一个常数M使得

≤M

(15)

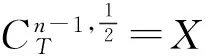
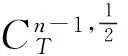
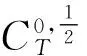
易知(Lx)(t)为反周期的，所以∀t∈[0,T].

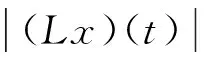
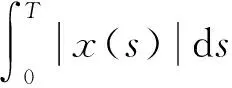
(16)

算子L是连续算子.定义算子

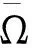
定义同伦变换:

根据式(15)知0∉Hλ(∂Ω),λ∈[0,1],由Brouwer度的同伦不变性，可得deg{I-F1,Ω,0}=deg{I,Ω,0}≠0.

3 应用举例

例1 考虑方程：

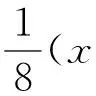
(17)

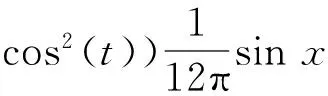
[1] XU J Z,ZHOU Z F.Existence and Uniqueness of Anti-periodic Solutions to an Nth-order Nonlinear Differential Equation with Multiple Deviating Arguments[J].Annals of Differential Equations,2012(28):105-114

[2] SHEN P,YAO X J,YANG J C.Existence and Uniqueness of Anti-periodic Solutions for a Class of Higher-order Differential Equation with Two Deviating Arguments[J].Guangxi Sciences,2011(18):22-25

[3] LI Y Q,HUANG L H.Anti-periodic Solutions for a Class of Lienard-type Systems with Continuously Distributed Delays[J].Nonlinear Analysis: Real World Applications,2009(10):2127-2132

[4] LUO F Q.Existence and Uniqueness of Anti-periodic Solutions for a Class of Lienard-type Equation with a Deviating Argument[J].Guangxi Sciences,2010(17):27-31

[5] 徐建中，周宗福.一个具有多个时滞变量n阶非线性微分方程仅周期函数解的存在唯一性[J].重庆工商大学学报(自然科学版)，2010，27(6)：545-550

XU J Z,ZHOU Z F.Anti-periodic Solutions for a Kind of Nonlinear Nth-order Differential Equation with Multiple Deviating Arguments[J].Chongqing Technology and Business University(Natural Science Edition),2010,27(6):545-550

[6] CHEN Y,NIETO J J,OREGAN D. Anti-periodic Solutions for Fully Nonlinear First-order Differential Equations[J].Math Comput Modelling,2007,46:1183-1190

[7] MAWHIN J.Periodic Solutions of Some Vector Retarded Functional Differential Equations[J].J Math Anal Appl,1974,45:588-603

[8] GUO D.Nonlinear Functional Analysis[M].Jinan:Shan dong Science and Technology Press,2002

责任编辑：李翠薇

Existence and Uniqueness of Anti-Periodic Solutions for a Class of High-order Differential Equation with Multiple Deviating Arguments

XU Jian-zhongl,ZHOU Zong-fu2
(1.Department of Mathematics, Bozhou University, Anhui Bozhou 236800,China;2.School of Mathematical Science, Anhui University, Hefei 230601,China)

deviating argument;Leray-Schauder degree;anti-periodic solution

2016-04-10；

2016-06-05.

国家自然科学基金(10771001)；安徽省教育厅自然科学基金( KJ20138153，KJ20132218)；安徽省质量工程项目(2016jyxm0681,2016jxt01050,2016gxk093);亳州学院科研项目(BZSZKYXM201302，BSKY201539).

徐建中(1979-)，男，安徽庐江人，副教授，硕士，从事泛函微分方程研究.

10.16055/j.issn.1672-058X.2017.0002.001

O

A

1672-058X(2017)02-0001-05