高速弹载雷达目标相参积累技术研究

张都川，文 才，刘 辉

(西安电子工程研究所，陕西 西安 710100)

高速弹载雷达目标相参积累技术研究

张都川，文 才，刘 辉

(西安电子工程研究所，陕西 西安 710100)

导弹高速运动带来的距离走动和多普勒扩展会影响目标的相参积累性能。针对这一问题，提出了基于惯导信息的运动补偿方法。该方法充分考虑了弹载雷达高数据率的要求，能够解决径向速度带来的距离走动和径向加速度带来的多普勒扩展。仿真结果表明，该方法可使信噪比约改善5 dB。

距离走动；多普勒扩展；运动补偿；相参积累

对海打击中，超音速导弹凭借突防能力强的特点有着广阔的应用前景。超高的飞行速度会给雷达导引头的目标检测带来一系列问题。文章主要针对导弹高速度运动对目标回波相参积累性能的影响进行研究。

在雷达制导系统中，Chirp信号是一种常用的发射脉冲信号，其工作原理是通过发射的宽脉冲信号和目标回波信号进行匹配压缩得到窄Sinc包络[1-2]。目标检测中，由于单个脉冲的回波能量有限，还需对压缩所得的Sinc包络进行相参积累来进一步提高信噪比。相参积累过程中，导弹高速运动会引起回波包络在不同脉冲重复周期之间发生走动，使得回波能量难以聚焦。当存在加速度或其他高次运动项时，回波信号的相位不再一致，能量会扩散到不同多普勒通道中，积累性能也会受到影响。为了提高目标回波的积累性能，需要对弹目之间的相对运动进行补偿。目前，运动补偿主要包括包络对齐和相位补偿两方面。包络对齐方法如：最小熵法[3]、包络插值移位法[4]、Keystone变换[5-7]等。相位补偿方法如：Chirp-Fourier方法[8]、分数阶傅里叶变换方法[9]，调频斜率估计方法[10-11]等。同时弹载雷达的高数据率对运算量有着很高要求，使得许多补偿算法难以工程应用。考虑到高数据率的要求，在补偿精度允许的条件下，基于传感器数据的运动补偿方法因运算量小，具有一定优势。

1 信号回波模型

假设雷达发射的是线性调频脉冲串，则其数学表达式可表示为

(1)

图1 导弹与目标的运动关系示意图

其中，导弹运动速度和加速度分别为vm和am，导弹与目标之间的初始距离为R0，α、β、φ分别为目标形心的方位角、俯仰角和波束宽度。由图1可得，导弹与目标之间的径向速度v=vmcosαcosβ，径向加速度a=amcosαcosβ。因此，第m个脉冲对应的弹目径向距离可表示为

(2)

与之对应的时延可表示为

(3)

因此可得基频回波信号

(4)

其中，fd=2v/λ。当v·X，BTP·1时，经过傅里叶变换，基频回波信号的频谱可近似表示为

(5)

对信号进行频域脉压，再经过逆傅里叶变换，最终得到经过脉压的回波信号

(6)

2 积累性能影响因素分析

在相参积累过程中，导弹高速运动引起的越距离单元走动和多普勒扩展现象会使得积累性能下降。文中以匀加速运动模型为例，研究了回波特性，分析了积累性能下降的具体影响因素。

2.1 回波包络项分析

由式(10)可得回波信号的包络项为

(7)

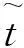
设积累脉冲数为N，为满足相参积累条件，通常要求相参积累时间内距离走动不超过1/4个距离单元，因此有

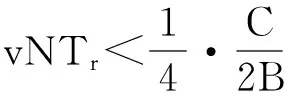
(8)

当径向速度超出了上述约束，回波包络会出现较为严重的越距离走动现象，影响相参积累效果。

2.2 回波相位项分析

由式(6)可得回波信号的相位项为

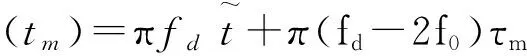
(9)

(10)

所以

(11)

相比于载频f0，导弹运动带来的多普勒频移fd可以忽略不计，因此式(11)可近似为

(12)

通过回波包络项和相位项的分析可以看出，距离走动主要取决于径向速度v，多普勒扩展主要取决于径向加速度a。

3 相参积累性能改善方法

回波信号的相参积累，可有效改善目标信噪比，有利于目标的检测。而导弹的高速运动会给回波信号相参积累带来困难，因此运动补偿是必要的。目前运动补偿的方法主要分两类：一是基于运动传感器的补偿，如惯导、GPS等；二是基于回波信息的补偿，如引言中所示的Keystone方法等。

3.1 基于惯导数据的运动补偿

目前惯性导航系统的速度测量精度可达到2 m/s，加速度测量精度可达到千分之一g(g为重力加速度)。由于目标在波束覆盖范围内的具体位置不确定，而惯导提供的数据为波束中心的速度和加速度，因此会带来测速偏差。由图1分析可得，波束覆盖范围近端带来的速度偏差更大，考虑到在对海打击中，大型目标的运动速度vt不超过20 m/s，因此可得最大速度偏差|Δv|max的表达式

(13)

设弹载雷达数据率为Ra，考虑到运算效率，脉冲积累个数N可取为

N=2-floor(log2(RaTr))

(14)

其中，floor(·)为取整函数。以表1中典型的高速弹载雷达参数为例。

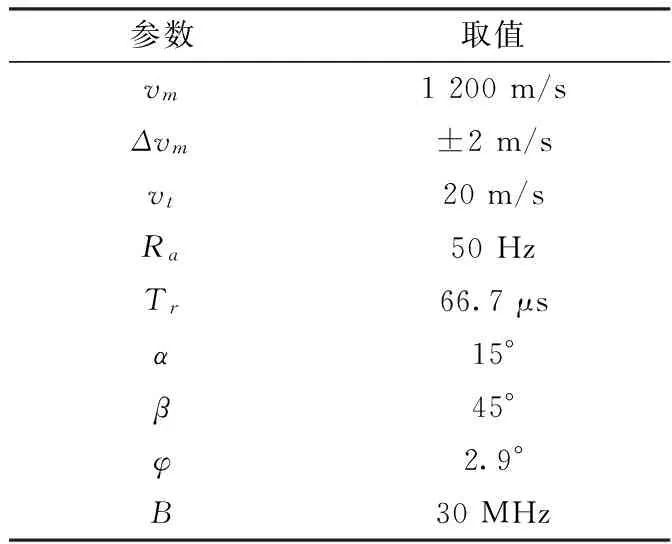
表1 弹载雷达参数取值

由式(14)可得N=256。结合式(8)可得速度限制项为73.24 m/s。由式(13)可得最大速度偏差不超过42.03 m/s2。导弹飞行过程中加速度可达10 g，结合式(12)可得加速度限制项为7.38 m/s2。参考最大速度偏差的计算方法可得最大加速度偏差不超过1.75 m/s2。综上，最大速度、加速度偏差均满足限制项要求，因此基于惯导数据的运动补偿是可行的。

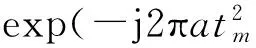
图2 基于惯导数据的运动补偿流程图

3.2 基于回波信息的运动补偿

基于回波信息的运动补偿中，最小熵法在低信噪比情况下对齐效果不佳。包络插值移位算法有着较高的对齐精度，但插值处理使得算法的运算量较大。频域校正算法[12]的运算量远低于包络插值移位算法，也有着较高的对齐精度，但不适于加速度或高次运动项存在的运动模型。针对匀加速模型，文献[13]提出的基于二阶 变换联合 处理的方法也存在低信噪比条件下估计精度不佳的问题。文献[14]介绍的广义二阶 变换算法，文献[15]介绍的基于检测前聚焦的三维GRFT算法都面临运算量和存储量过于庞大的问题，不适于工程应用。

针对相参积累中存在的运动补偿问题，需要兼顾补偿精度和运算量。目前基于回波信息的补偿算法在简单的运动模型中有着较高的补偿精度，但在实际应用中，由于弹体与目标之间运动关系相对复杂，这些算法的性能会受到很大影响，同时高补偿精度带来的大运算量也会成为制约。因此在实际应用中，基于回波信息的补偿算法多用于实时性要求不高的系统中，而在实时性要求较高的系统中，可利用惯导或其他运动传感器的数据进行补偿。

4 仿真实验结果

结合回波特性分析，给出仿真结果(参数取值：波长λ=8.6 mm，载频f0=35 GHz，脉冲重复周期Tr=66.7 μs，带宽B=30 MHz)。图3为速度和距离走动的关系图，Δr=1.25 m为相参积累所允许的最大距离走动量(1/4距离单元)。由图中可以看出，速度越大，包络距离走动越严重，脉冲积累个数越少，如v=1 200 m/s时，脉冲积累个数不超过15个。图4为加速度与回波相位的关系图，Δφ=1/2π为相参积累允许的最大相位差。由图可以看出，加速度越大，回波相位差越大，脉冲积累个数越少。如a=10g时，脉冲积累个数不能超过70个。图5为加速度补偿前后积累性能对比图，由图可以看出，不对加速度进行补偿会使得信号主瓣展宽，幅度下降，这与第二章的理论分析相一致，因为加速度的存在使得信号相位与慢时间呈二次关系，相参积累后会出现近似矩形的包络。而对加速度进行补偿后，信号相位与慢时间呈线性关系，再进行相参积累会出现sinc包络。相比于矩形包络，sinc包络具有更窄的主瓣，同时加速度的补偿使得信号幅度有了一定提高，如图5所示，补偿后的回波信噪比增加了5.45 dB。

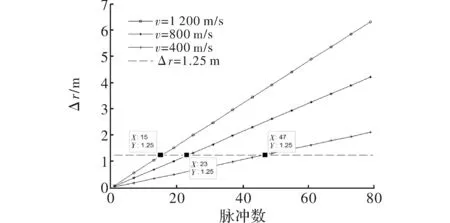
图3 速度对距离走动的影响

图4 加速度对回波相位的影响

5 结束语

弹目之间的相对高速运动会引起回波包络的越距离单元走动，同时当存在高次运动项时还会出现多普勒扩展现象。上述两个因素会严重影响多脉冲相参积累的性能。本文以径向匀加速运动为例，给出了信号的回波模型，通过对目标回波特性的详细分析，阐述了速度和加速度对距离走动和多普勒扩展的影响。结合回波特性分析结果和导弹高数据率的要求，提出基于惯导数据的运动补偿方法，通过理论分析和仿真实验验证了该方法的可行性和有效性。

[1] 朱永锋,李为民,陈远征,等. Chirp雷达对高速运动目标有效相参积累的算法研究[J].系统工程与电子技术,2004,26(10):1396-1399.

[2] 王远模,马君国,付强,等.高速运动目标的积累检测研究[J].现代雷达,2006,28(3):24-27.

[3] 邢孟道,保铮.一种逆合成孔径雷达成像包络对齐的新方法[J].西安电子科技大学学报,2000,27(1):93- 96.

[4] 王婷婷,王俊.Chirp雷达的两种有效积累算法的研究[J].航天电子对抗,2006,22(6):33-35.

[5] Perry R P，DiPietro R C，Fante R L. SAR imaging of moving targets[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(1):188-200．

[6] 谢纪岭,王彩云.基于距离走动校正和多普勒高阶项补偿的高超音速目标检测方法[J].宇航学报, 2011,32(9): 2002-2008.

[7] 李春林,吴琳拥.基于Keystone变换的长时间相参积累研究[J].电子科技,2013,26(6):148-152.

[8] Xia Xianggen.Discrete chirp-fourier transform and its application to chirp rate estimation[J].IEEE Transactions on Signal Process,2000,48(11):3122-3133.

[9] Guan J,Chen X L, Huang Y,et al. Adaptive fractional fourier transform based detection algorithm for moving target in heavy sea clutter[J].Radar, Sonar&Navigation,Iet,2012,6(5):389-401.

[10] 崔刚,李涛.一种基于二分法的LMF调制斜率估计算法[J].电子科技,2015,28(10):15-17.

[11] Raveh I,Mendlovic D.New properties of the radon transform of the cross wigner/ ambiguity distribution function[J].IEEE Transactions on Signal Processing,1999,47 (7):2077-2080．

[12] 夏卓卿,陆军,陈伟建.一种Chirp雷达包络对齐新方法[J].雷达科学与技术,2010,8(1):44-48.

[13] Tian Jing, Cui Wei, Shen Qing,et al.High-speed maneuvering target detection approach based on joint RFT and keystone transform[J].Science China :Information Sciences,2013,56(9):1-13.

[14] 张作霖.雷达高速弱目标长时间积累方法研究[D]. 哈尔滨:哈尔滨工业大学,2014.

[15] 蒋千.高速目标雷达信号长时间积累技术研究[D]. 成都:电子科技大学,2013.

Study on Coherent Integration for High-speed Missile-borne Radar

ZHANG Duchuan, WEN Cai, LIU Hui

(Xi’an Electronic Engineering Research Institute, Xi’an 710100,China)

Range migration and Doppler spread caused by high-speed motion of radar seeker would affect the performance of coherent integration. To solve this problem, a novel motion compensation method based on the inertial navigation system is proposed. In the proposed method, the high data rate requirement of missile-borne radar has been fully considered, and the range migration caused by radial velocity and the Doppler spread caused by radial accelerator could be removed. Simulation results show that there is about 5dB signal-to-noise-ratio improvement using the proposed method.

range migration ; doppler spread ; motion compensation ; coherent integration

2016- 09- 14

张都川(1989-)，男，硕士。研究方向：精确制导技术。文才(1986-)，男，博士。研究方向：阵列信号处理等。刘辉(1974-)，男，博士，高级工程师。研究方向：雷达导引头技术等。

10.16180/j.cnki.issn1007-7820.2017.03.048

TN957.52

A

1007-7820(2017)03-174-04