激光位移传感器检测类圆弧工件表面研究

姜 松，张仁杰，李倩倩，刘禹辰

(上海理工大学 光电信息与计算机工程学院，上海 200093)

激光位移传感器检测类圆弧工件表面研究

姜 松，张仁杰，李倩倩，刘禹辰

(上海理工大学 光电信息与计算机工程学院，上海 200093)

基于直射式点激光三角法原理，分析测点表面法向与投射激光间夹角变动引起的误差情况，提出采用另设的倾斜传感器，专门对因单一传感器测量时的不准确区段进行检测，根据曲率半径确定可信区段、并通过两传感器可信区段的拼接，实现不同半价圆弧衔接构成的截面型线上各点的检测。经实验验证表明，对表面曲率半径>20 mm的圆弧，测量误差<100 μm。

曲面检测；激光位移传感器；三角法测量；可信区段

在工业生产过程中，测量作为重要的检测技术[1-3]，常对各种零部件的表面轮廓进行检测。一般情况下，这类检测多采用接触式传感器进行。但在某些特殊场合，接触式检测难以实施，需采用以激光位移传感器[4-5]为代表的非接触式检测装置，但此方法易受工件表面锈斑、油污、粉尘、粗糙度、法向角等因素的影响，因而在实际应用过程中受到限制[6]。对具有曲面形状工件的轮廓度检测，除采取一定措施控制锈斑、油污、粉尘的影响外，还要解决测点表面的法向角变动的影响。

1 激光测量原理

激光位移传感器的基本工作原理是光学三角法，即利用光学的散射特性和成像特性，通过对传感器中光学探测器成像光斑的光能质心的变化来推测被测对象的位移变化。如图1所示的是激光位移传感器的三角测量法的原理图[7-8]，主要包括：半导体激光器、会聚透镜、接受透镜，被测对象，探测器和后续信号处理电路。当被测表面位于M位置时，传感器的成像光斑为N点；当将被测物向上移动Δ1到M1时，引起光斑像点在光电探测器上的位移为Δ2，此时Δ2=NN1。计算可得位移

图1 激光三角法测量原理图

(1)

其中,θ0为入射光线与接收透镜光轴的夹角；θ1为两条反射光线的夹角；θ2为光电探测器的接收面与接收透镜光轴的夹角；l为接收透镜物镜；l′为接收透镜的像距。被测物面相对于参考平面M上移时，取正号，下移时取负号。

为了保证被测对象可清晰地聚焦在光电探测器上，该激光光束应该满Scheimp-flug条件[8]：像平面、物平面、透镜平面相交于一条直线，即满足tanθ0=βtanθ2，其中β为探测器横向放大率。此时当物体发生一定程度的移动时，传感器的光电探测器上都有散射光形成的成像光斑，确保了测量的准确性。

2 表面倾角误差分析

2.1 倾斜误差产生

激光三角法无误差的前提是发射光线与被测物体表面法线的夹角始终为零。当被测表面上入射光点处的法线与入射光方向不重合时，即被测表面发生了倾斜，其夹角称为法向角。入射光点所产生的散射光空间分布将发生变化，将造成在光电接收器上的像光斑的光能质心相对于其几何中心发生偏移，这样实际测量结果与三角法测量原理公式的理论计算结果有一定偏差量，为此我们建立了相应的圆柱截面轮廓倾斜误差[9-11]的数学模型。

2.2 可信区段和临界值的划分

文中利用垂直传感器对不同半径(主要有29.97 mm，39.95 mm和49.74 mm)下的圆柱型工件部分轮廓截面进行测量分析，以确定每一个半径下所对应的可信区段，下面以29.97 mm半径的圆柱为例。

表1 测量直径为29.97mm圆柱的误差 /mm

首先利用多次测量确定圆柱型截面的顶点值，保证误差在允许范围之内，然后在此点的两侧取两点开始测量，保证取得点的误差<100 μm以内，分别以这两点开始向两边以1 mm或2 mm间隔测量取点，直至超出测量量程为止。其中靠近顶点两侧取的两点可根据直径的变大而增加其横坐标。在测量39.95 mm直径圆柱时选取±5；49.74 mm圆柱选取±10。测量直径为29.97 mm圆柱数据如表1所示。

如表1所示，误差随测点与顶点的水平距离的增大而变大。测量范围在-6～9 mm以内，误差均>100 μm，当在12.37 mm和-14.91 mm时，均达到测量的最大量程。

同理可分别测量出关于39.95 mm和49.74 mm两个半径圆柱截面的误差范围。在此文中定义将测量外圆柱形上凸截面轮廓或内圆柱形下凹截面轮廓的顶点或谷点的横坐标定为0，其左右的误差是在100 μm以内的测量点的横坐标范围定为可信区段。为了处理在实际应用中的场合，文中可利用插值拟合出常见未知测量半径的圆柱型截面轮廓的可信区段，如表2所示。

表2 可信区段划分

3 类圆弧型截面轮廓误差实验

3.1 检测装置系统

如图2所示，搭建了基于激光位移传感器检测系统实物图，主要有4部分构成：待测工件，激光位移传感器，光栅尺及PC计算机。首先将两个激光位移传感器分别固定于可以调节高度的竖直支架上，保持一定夹角，连接上位机[12-13]和光栅尺，接着调整激光器与待测物体间的位置，保证正确测量数据。在测量中只需替换测量工件即可。

图2 测量系统实验装置图

3.2 类圆弧型截面轮廓测量

诸多被测工件的截面是由各种半径的圆弧衔接构成的，为此采用综合垂直与倾斜两传感器可信区段确定实际圆弧截面轮廓。

(1)垂直传感器测量。从工件一端开始测量，以1 mm为间隔移动光栅尺传感器，记录每个点水平位移(横坐标)和垂直高度(纵坐标)，直到不可测量点结束。确定轮廓线上凸顶点或下凹谷点，利用其左右两个相邻点的坐标，根据最小二乘法[14-15]求出拟合圆，确定曲率半径，利用上文的计算方法得出相应的可信区段，并根据此坐标与工件截面轮廓上对应点的差值即得误差。

垂直激光位移传感器测量数据及相应误差如图3所示，在-12.63～11.37、20.37～30.37、45.37～51.37、59.37～93.37范围内，是可信区段，其误差均<100 μm。同时也会存在其他点的误差<100 μm，因为可信区段是保守估计;

(2)倾斜传感器测量。倾斜传感器利用与垂直传感器相同的方法进行测量，但因为坐标系的不同需要进行相应的坐标变换。

图3 垂直激光位移传感器测量数据图示与误差图

1)首先将测量数据转化成与垂直传感器测量数据所用的坐标系。如图4所示，l1和l2分别为垂直和倾斜激光位移传感器测量读数，α为两个传感器入射光线夹角，Δy0和Δx0分别为两个传感器的垂直和水平距离。点A和点B分别为倾斜和垂直传感器的入射光线形成的点，其坐标分别为(x′,y′)和(x,l1)，经转化后A点坐标为(x-Δx0+l2sinα,l2cosα+Δy0);

图4 坐标转换图

2)经过上述变换，此时A点横坐标发生偏移，为了保证与垂直测量下对比，需要进行横坐标匹配。由于此时每间隔的两点穿插着相对于的垂直传感器测量点，我们利用线性插值法计算出与垂直传感器相同的点坐标A1;

3)为了准确划分倾斜传感器测量下的可信区段，还需要将A1的坐标系做旋转α角度的变换，其中α角为倾斜与垂直传感器出射光线的夹角。假定坐标A1(x,y)和A2(x′,y′)分别转换前后的坐标点，则A2坐标为(ysinα+xcosα,ycosα-xsinα)。

绘制A2的曲线轮廓图，利用垂直测量下的方法确定可信区段，随后再将轮廓图反旋转-α度，即得数据A1的可信区间，如图5显示的是倾斜传感器下测量误差曲线图，横坐标在-16.63～-1.63、27.37～38.37、39.37～45.37、76.37～95.37范围内，是可信区段，其误差均<100 μm，同时也会存在其他点的误差<100 μm。

(3)综合分析。根据对比两者的测量结果，可将倾斜和垂直激光位移传感器测量的可信区段进行组合。1)对于垂直和倾斜传感器测量的所有可信区段，直接保留;2)对于垂直和倾斜传感器测量的所有可信区段内的数据点均存在的情况，取垂直测量的数据点;3)在非可信区段取垂直传感器测量的数据点。

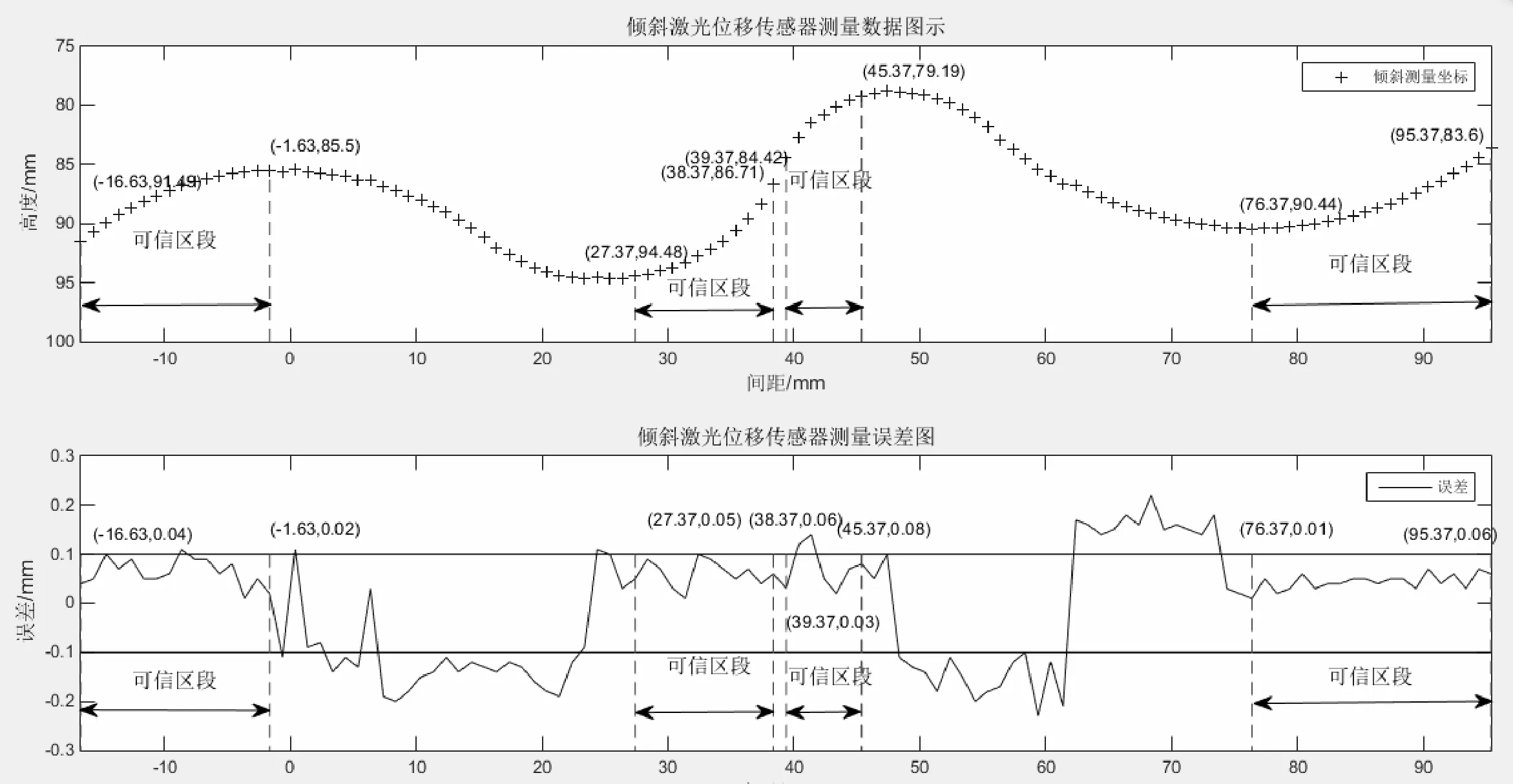
图5 倾斜激光位移传感器测量数据图示及误差图

根据上述方法，文中得到了两激光位移传感器可信区拼接后的测量数据轮廓及其相应测量误差如图6所示。此方法可测量大部分区段，只有少部分不能测量，获得连续轮廓线的可信数据点，其测量误差不超过0.1 mm。

图6 两传感器可信区拼接后的测量数据及测量误差图

4 结束语

本文设计并搭建了类圆弧截面轮廓测量装置，对因表面倾斜引起的误差进行试验测试，提出了另设倾斜激光位移传感器测量法，根据不同可信区段的数据拼接实现对类圆弧截面轮廓的测量。经实验验证表明，对表面曲率半径>20 mm的圆弧，测量误差<100 μm。本研究结论，对于扩展激光三角法传感器适用范围及提高曲面轮廓的测量精确度，具有一定参考价值。

[1] 裘祖荣,石照耀,李岩.机械制造领域测量技术的发展研究[J].机械工程学报,2010,44(14):1-11.

[2] 冯其波.光学测量技术与应用[M].北京:清华大学出版

社,2008.

[3] 刘先卓,王树奎,陈锦生,等.激光测量技术及其应用[J].机械设计与制造,2003(3):95-96.

[4] 王晓嘉,高隽,王磊.激光三角法综述[J].仪器仪表学报,2004,25(z3):601-604.

[5] 冯俊艳,冯其波,匡萃方.高精度激光三角位移传感器的技术现状[J].应用光学,2004,25(3):33-36.

[6] 常城,张志峰.激光三角法测量的误差研究[J].中国科技信息,2006(23):61-62.

[7] 吴剑锋,王文,陈子辰.激光三角法测量误差分析与精度提高研究[J].机电工程,2003,20(5):89-91.

[8] 李兵,孙彬,陈磊,等.激光位移传感器在自由曲面测量中的应用[J].光学精密工程, 2015, 23(7): 1939-1947.

[9] 李冬冬,王永强,许增朴,等.激光三角法在物面倾斜时的测量误差研究[J].传感器与微系,2015,34(2):28-29.

[10] 王文卓,李大勇,陈捷.表面粗糙度非接触式测量技术研究概况[J].机械工程师,2004(11):6-9.

[11] 温新,周云飞,穆海华,等.激光测量几何误差补偿算法[J].机械设计与制造,2011(9): 46-48.

[12] 龚建伟,熊光明.Visual C++/Turbo C串口通信编程实践[M].2版.北京:电子工业出版社,2007.

[13] 肖定国,宣华.用VC实现PC机对激光位移传感器的通信控制[J].控制工程,2005(S1): 136-138.

[14] 田社平,张守愚,李定学,等.平面圆圆心及半径的最小二乘拟合[J].实用测试技术,1995(5): 23-25.

[15] 陈光,任志良,孙海柱.最小二乘曲线拟合及Matlab实现[J].兵工自动化,2005,24(3):107-108.

Research on the Surface of Circular arc Workpiece by Laser Displacement Sensor

JIANG Song，ZHANG Renjie，LI Qianqian，LIU Yuchen

(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

On the basis of the principle of direct laser triangulation method, analysis detected surface point method and laser projection angle between the changes caused by the error, is proposed in this paper to separate the tilt sensor, specifically for detecting the single sensor measurement inaccurate section, determined channel section, and two sensor confidence section through splicing, to achieve different half arc connection a section line the detection based on the curvature radius. Experimental results show that the radius of curvature of the surface is larger than that of 20 mm, and the measurement error is less than 100 μm.

surface detection; laser displacement sensor; triangulation measurement; trusted section

2016- 04- 13

姜松(1991-)，男，硕士研究生。研究方向：仪器科学与技术。

10.16180/j.cnki.issn1007-7820.2017.03.022

TN294;TP212

A

1007-7820(2017)03-079-04