太极拳的弹性力学

顾 杰，郭振兴



太极拳的弹性力学

顾 杰，郭振兴

（邯郸学院 太极文化学院，河北 邯郸 056005）

讨论了功架的弹性功能，将文献[1]的弹簧功用弹性力学原理来诠释。推手时人体在外力作用下产生弹性变形，还可以引进攻防所需的有计划的变形。人体弹簧系数可用串联模型来模拟。定量分析证明了“化宜柔，发宜刚”的直观结论。

力学；弹性；人体；模型；太极拳

一、发力和发劲的同异

图1中的手向右方水平方向对一堵垂直的光滑的墙发劲。结果产生一对力：手对墙的向右的力，用黑色箭头表示；墙对手的向左的力，用红色箭头表示。这是一对作用力和反作用力。根据牛顿第三定律，它们大小相等，方向相反。图中攻势水平向右，可以说手向右发劲。手对墙的推力水平向右，可以说手向右发力给墙。本例的发劲和发力差别不大，可以说发劲达到了发力的目的。

图2中的手向右方水平方向对一堵水平的光滑的墙发劲。结果没有产生任何力。图中攻势水平向右，可以说手向右发劲。但是墙水平又光滑，没有力产生。本例发了劲，但没有达到发力的目的。

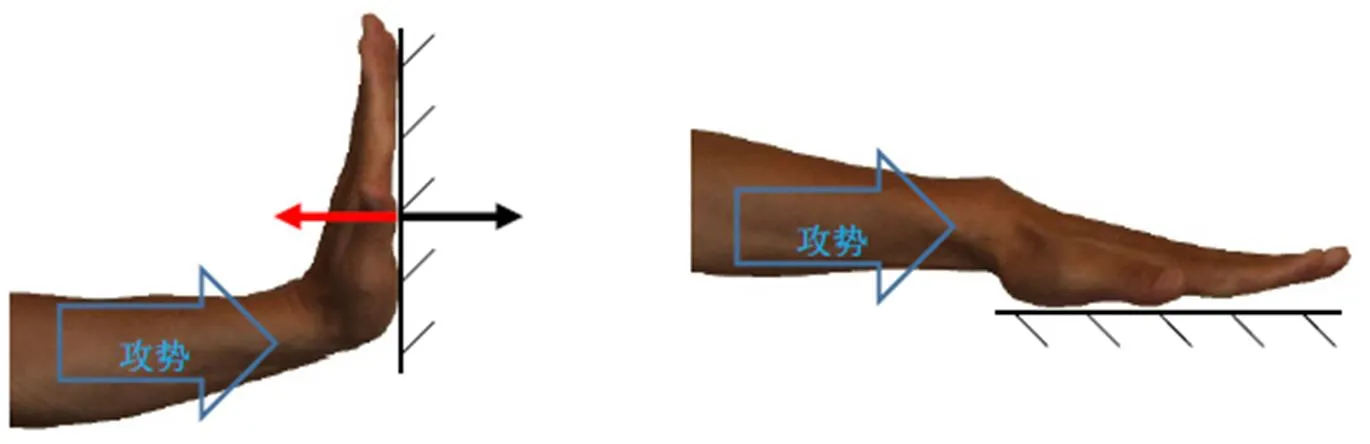
通过这两个例子可以看出，发劲和发力有联系，但不是一回事。什么是发劲，什么是发力呢？在武术界这是一个很有争议的话题。这里将用力学的语言给它们下定义。

发劲的定义：发劲由意念指导形成动量和运用动量。这里的动量包括支撑动量（由地面支持的静态动量）、整体动量和相对动量。

发力的定义：发力是由发劲形成的动量和对方的动量相互作用产生的力。可由意念指导这个力去攻击对方的平衡，同时保持我方平衡。

可见发劲是“知我”的过程，发力则是协调“知我”和“知彼”的对抗过程。

两方接手时的实际情况既不是图1的全数反力，也不是图2的全无反力，而是介于图1和图2之间的弹性作用。

二、水平力的弹性模型

假设我方发一个水平推力，见图3。可以把接手处和上体质心间的机体简化为一个弹簧，把质心和地面间的机体也简化为一个弹簧。

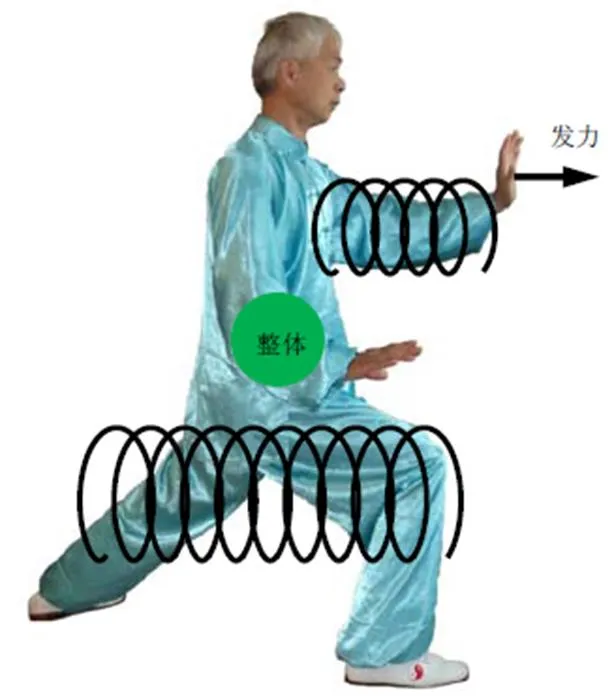
图3 水平力时的我方的弹性模型

力学上这是一个串联体：我方是地面、下盘弹簧、质心、上盘弹簧和接手质量的串联体，见图4左图。两方接手中间将产生力。如果我方发的是水平推力，则这个推力作用于对方。一个大小相等方向相反的反作用力作用于我方，图4左方是我方的隔离体。注意图3中的“发力”的反向力作用于图4左图的我方。类似的可以作出对方的隔离体图，见图4右图。

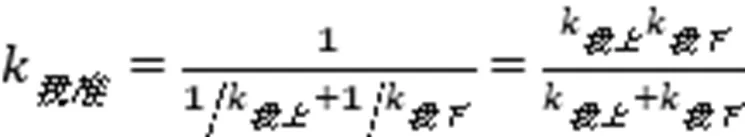
图5我方胡克定律

可以证明

所以串联弹簧比较软，或者说弹性系数较小。

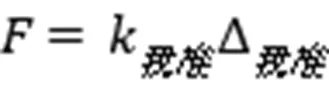
这是说弹性系数和变位成反比：弹簧越刚变位越小，弹簧越柔变位越大。太极拳要柔中带刚，刚柔相济。太极弹簧功用力学的术语来描述有两个方面：其一是要能刚能柔，即有变化弹性系数的能力；其二是化时宜柔，发时宜刚。

打太极拳时要能刚能柔，即有变化刚柔能力。太极拳的一个要领是“松”，松是内在的要求。而“柔”是外在表现。内在的松首先是意念要指导松，然后有肌肉、关节和韧带的放松。长久的练松可以将松融入下意识的条件反射性行为。松的力学效果是解除僵劲，使关节灵活、韧带富有弹性，肌肉张缩有致。内在的松导致外在的柔，柔的力学效果是进退自如、不丢不顶。这是经典推手理论中的沾和连。可以说松是内功，柔是防御的技术。太极拳并不排除“刚”，只是不主张一味的“刚”。“刚”是外在表现，其对应的内在要求是“劲”。长久的练劲可以将劲融入下意识的条件反射性行为。劲的力学效果是解除僵劲，使关节灵活、韧带富有弹性、肌肉张缩功能强，防时有抵抗功能，攻时有发劲功能。内在的劲导致外在的刚，刚的力学效果是发引自如、借势加力。这是经典推手理论中的粘和随。可以说劲是内功，刚是进攻的技术。这么说内功有松和劲，可以用劲度来度量。劲度的左端是松，右端就是劲，见图6。相应的外在力学效果是柔和刚。可以用弹性系数来度量。弹性系数小（左端）是柔，弹性系数大（右端）是刚，见图7。练左端可以立于不败之地，练右端可以成为长胜将军。练刚柔的变换功能才能臻至上乘功夫。这是经典理论中的阶及神明。

图6 劲的度量

图7 弹性系数的度量

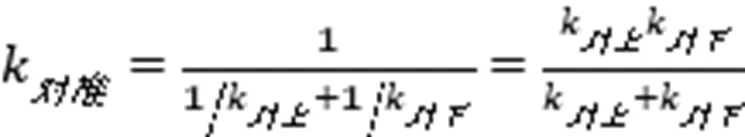
可以证明

图8 对方胡克定律

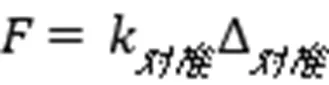
两方接手连成一体，图9是联合体的隔离体图。这时的作用力和反作用力是为联合体的内力，不在隔离体图中示出。作用于体系的两端是双方脚底的摩擦力。这个力作用于一个由四个弹簧串连起来的弹簧上，在接手处产生变位。

串联弹簧的弹性系数是，

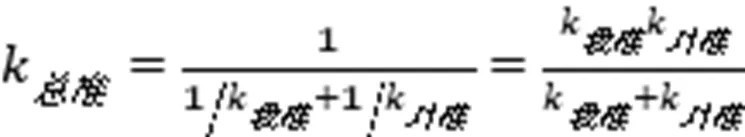
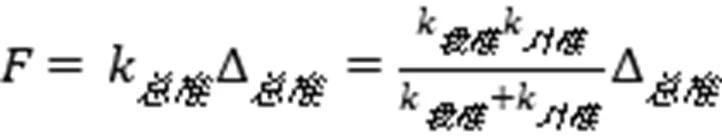
由（8）式可见，作用力随我方弹性系数的增长而增长，见图10。作用力和对方弹性系数的关系类似。弹性系数小就是柔，弹性系数大就是刚。所以柔可以产生小的作用力，这是“化”需要的力学功能；刚可以产生大的作用力，这是“发”需要的力学功能。哪一方都能运用这个柔化刚发的力学原理。

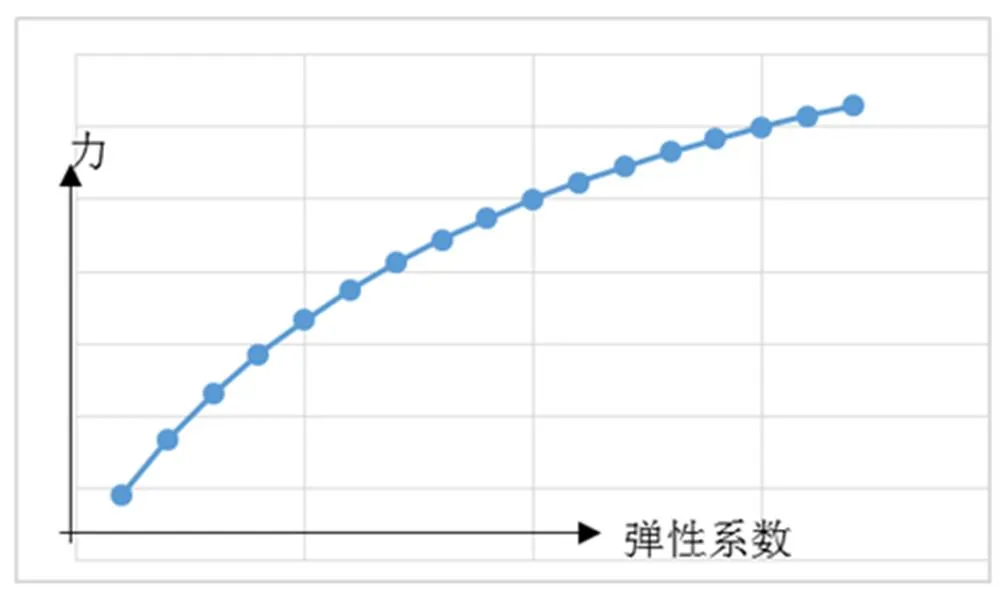
图10 接手联合体的隔离体

解（3）式和（8）式得，

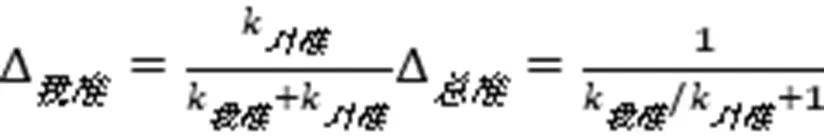
（9）式说明我方变位由总变位分配而来，分配量是我方和对方弹性系数之比的函数。见图11，比值小时我方柔对方刚，我方的变位大；比值大时我方刚对方柔，我方的变位小。粗略的说是变位和我方的柔度成正比：我方越柔，变位越大；我方越刚，变位越小。这个结论对对方也适用。这就是说己方越柔，变位越大；己方越刚，变位越小。在化解时柔度大可以减小力，是有利的方面；但柔度大会引起大的变位，可能会将对方引入己方重心，是不利的方面。所以引进是有限度的，柔度不能太大。

类似的，解（6）式和（8）式得，

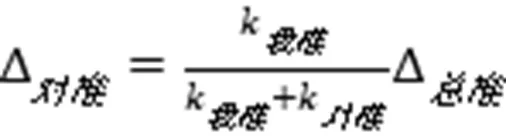
由（9）式和（10）式得，

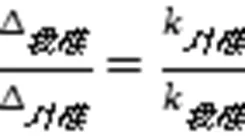
（11）式再次表明两方的变位和两方的弹性系数成反比，和两方的柔度成正比。

由图3和（1）式的考虑，人体由上盘弹簧和下盘弹簧串联而成。由（2）式和（5）式串联弹簧比各自的上盘弹簧或下盘弹簧软。上盘弹簧主要由接手和上体间的肢体构成。手臂撑圆、垂肘等太极要领使工架具有自动的弹性。意念主导的变换接手和上体间的距离使功架具有主动的弹性。下盘弹簧主要由两脚和腰胯间的肢体构成。弓步、坐步等太极步型有一些弯弧处，使工架具有自动的弹性。意念主导的步型变换使功架具有主动的弹性。

由（3）可算出我方接手处的变位。为了算出质心处的变位，先列出下盘弹簧的胡克定律，

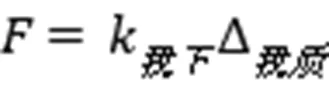
解（3）式和(12)式得，

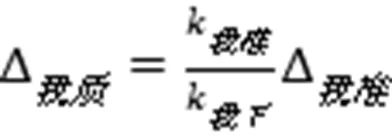
将（1）式代入(13)式得到质心处的变位，

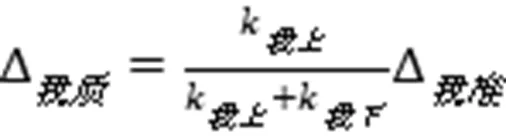
类似的可得到对方质心处的变位，

三、一般情况的弹性公式

攻势的方向一般和发力方向不同。例如图12，水平攻势遇到有摩擦的斜面。这时产生一个正压力分量和一个摩擦力分量，合力一般不再水平，合力通常会有一个垂直分量。又如图13，水平攻势遇到有倾斜的胸平面。这时产生一个法向力分量和一个切向力分量，合力一般不再和攻势方向一致，合力通常会有一个横向分量。

图12 水平攻势斜面

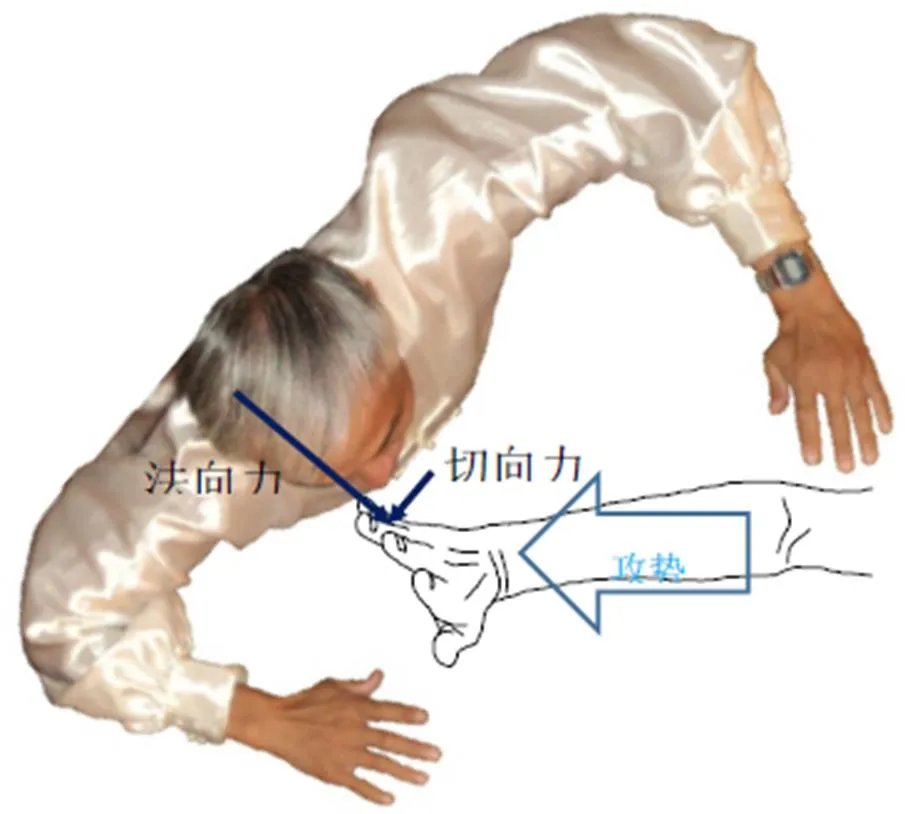
图13 反弹作用力的生成

一个攻势会有三个线性分量，对方接招后产生三个线性发力分量。受对方接招方式的影响，发力的方向一般不和攻势方向相同。

太极推手可以认为是两个刚体的相互作用。刚体的相互作用有六个力的分量：三个线性分量和三个旋转分量。所以一个一般的攻势会有三个线性分量和三个旋转分量，对方接招后产生三个线性和三个旋转发力分量。受对方接招方式的影响，发力的方向一般不和攻势方向相同。攻势包括三个方向的支撑动量、整体动量、相对动量和三个方向的支撑旋转动量、整体角动量、相对角动量。发力包括三个方向的力和三个方向的力矩。

扩展（1）式和（4）式，

(16)式对我方和对方都适用。(16)式假定人体构成六个串联弹簧，三个线性弹簧和三个旋转弹簧，它们之间没有相互作用。扩展（3）式和（6）式，接手处的弹性公式为：

类似于(8)式，广义力和总变位的关系是：

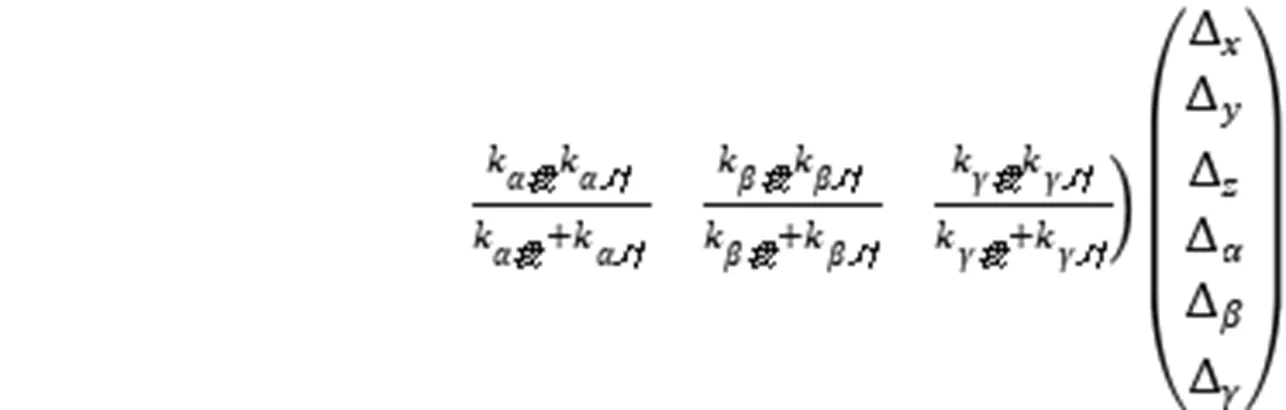
四、线性理论

广义变位矢量有六个分量，这些分量对人体的位置和角方位都有影响。在计算接手力时[2][3]忽略了这些影响。有两个原因允许或导致了这些忽略。首先，这些变位和人体变位前的位置相比较小，忽略引起的误差不大。其二是计算力时还不知变位，要算出力后才算变位。理论上可以把变位加入原来的位置，重新算力；再由新力重算变位。如此迭代已达合适的精度。迭代法将引入大量的计算，而且其收敛性需要得到证明。

忽略变位对力计算的影响是线性理论。线性理论忽略了变位和力的相互影响，忽略了二阶误差，可用最小的运算量获得足够的计算精度。工业界广泛运用线性理论。

例如绗架的设计，建筑师在计算力时只用绗架的原形尺度（图14），再把力作用于绗架来计算其变形（图15）。建筑师用的就是线性理论。

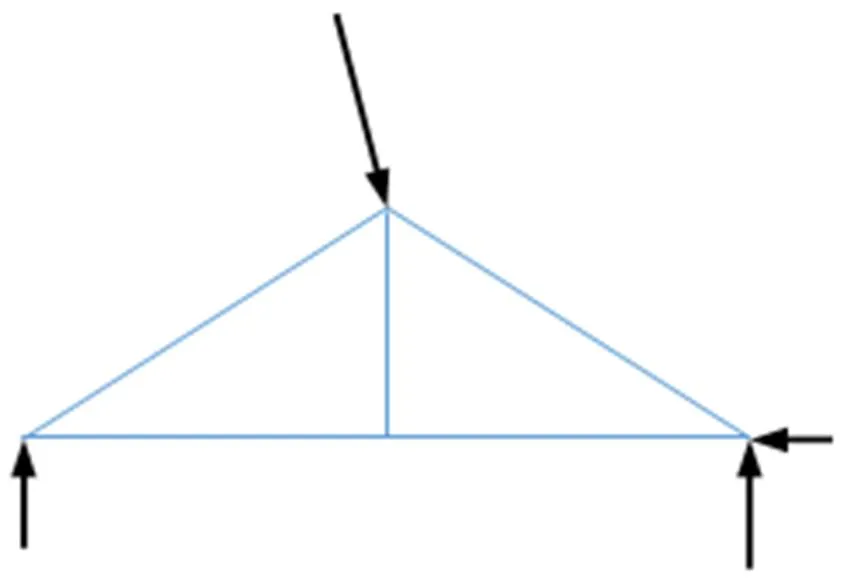
图14 绗架受力

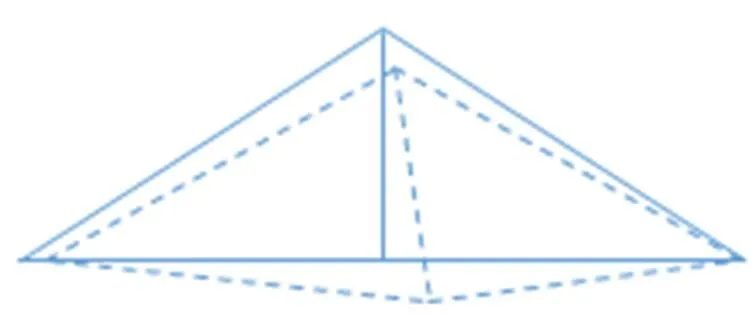
图15 绗架变形

文献[2][3]的接手力的计算和本文的弹性变位计算也运用了线性理论的概念。突出本质，忽略次要因素，简化计算。

五、线性位移和旋转位移，旋转位移和反关节限制

由(17)式可以算出接手处的变位。前三项是线变位，将略微改变接手的位置[2]。 (16)式是串联弹簧的性质。由(16)和(17)式可以将接手出的变位分配给质心处，即算出质心处的六项变位。类似于(14)式和(15)有：

(19)式对两方都适用。这些变位将略微改变质心的位置[2]。如果有必要，接手和质心的线变位可以代入文献[2][3]中的公式作第二轮力的运算。

接手处总位移可以分配给两方，（9）式和（10）式可以推广为：

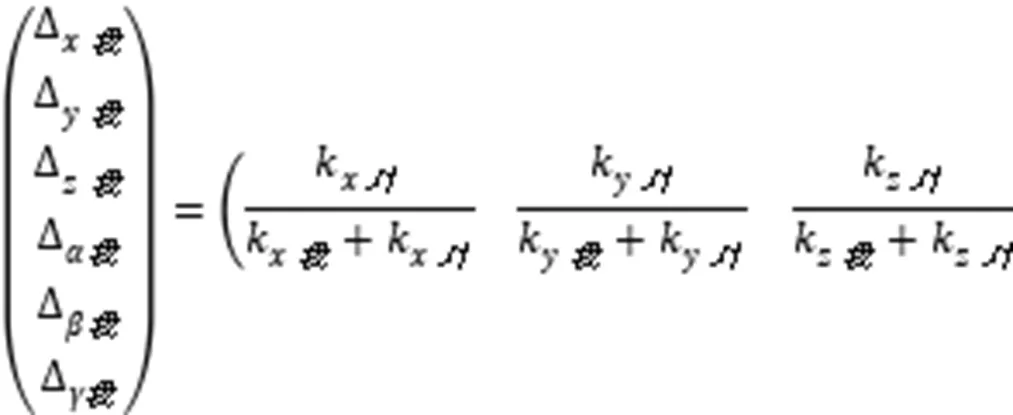
(17)式、(18)式、(20)式的后三项是角变位。(18)式是总的角变位范围，(20)式是分配给各方的角变位范围。变化范围是在肢体保持弹性功能的最大变位区域，实际的变位还和起始位置有关。见图16，因为“起始位置”介于“弹性始位”和“弹性终位”之间，“实变范围”小于“可变范围”。当角度达到“弹性终位”时，肢体达到反关节运动范围的极限。超过这个极限将引起肢体受损，为了避免受损只能运动其他肢体来避免这个极限。这个避免运动通常和杠杆原理有关，杠杆原理将导致受力方被掀翻。发劲发生在“实变范围”内。

两方对扭时，各自的扭角和自己的弹性系数成正比。但是由于起始位置的选择，离终位的距离不同。

图16 事实变位小于可能变位

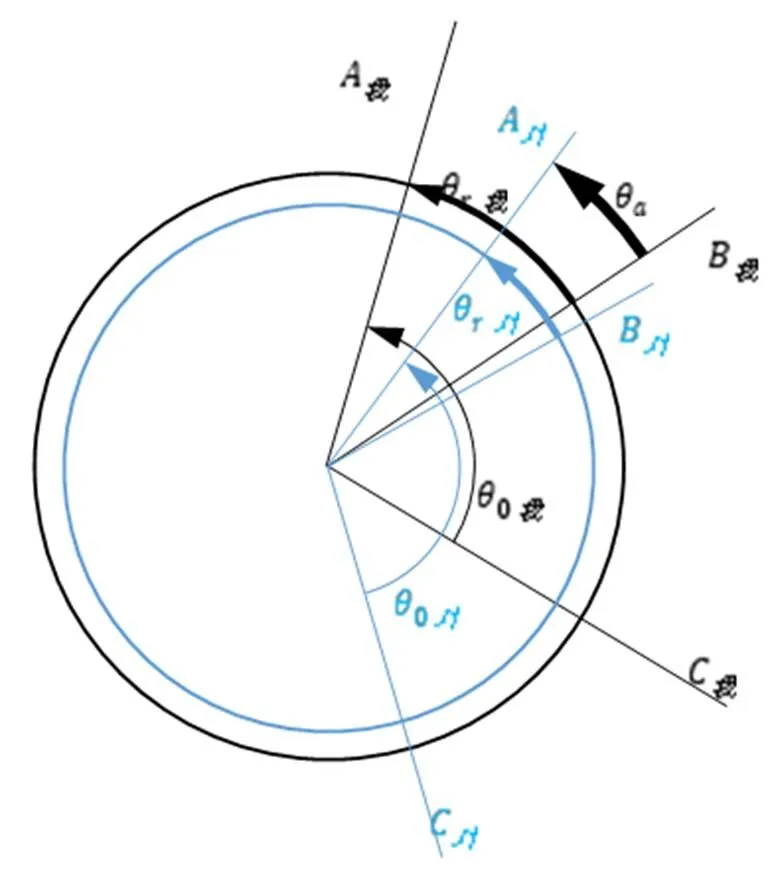
图17 攻方要让对方达到极限

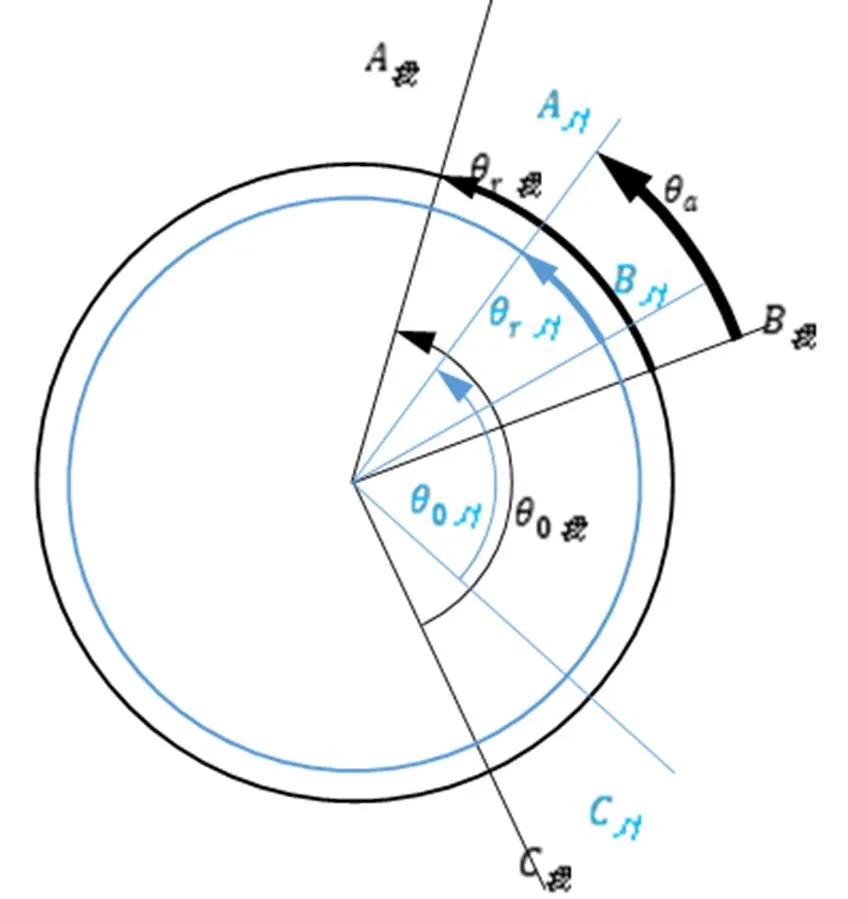
图18 守方要避免己方达到极限

六、分析例子

1. 右搂膝拗步

右搂膝拗步见图3。由文献[3]的公式的计算，得出表1。

表1 右搂膝拗步的水平临界力计算

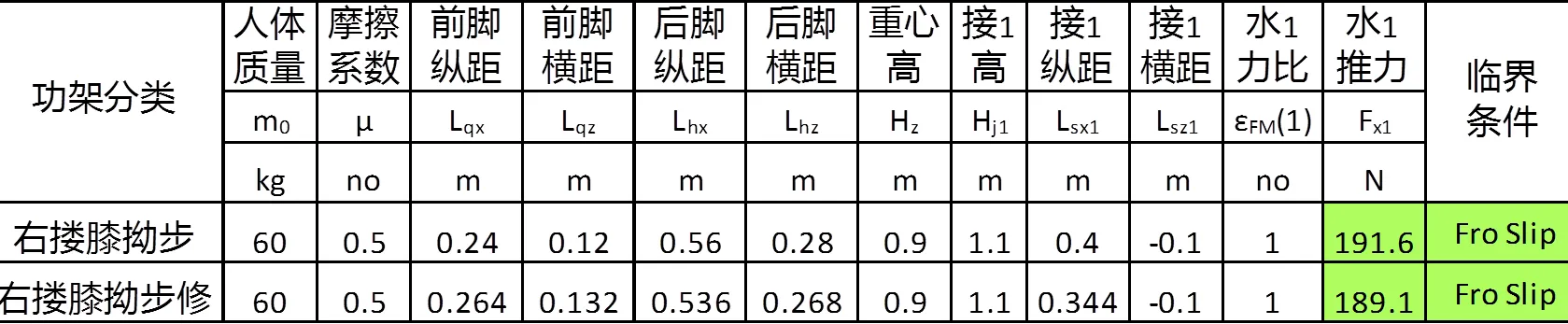
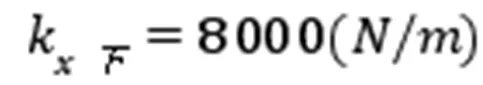
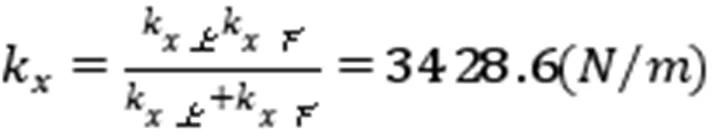
由（17）式第一式得接手处变位，

由(19)式第一式得质心处变位，

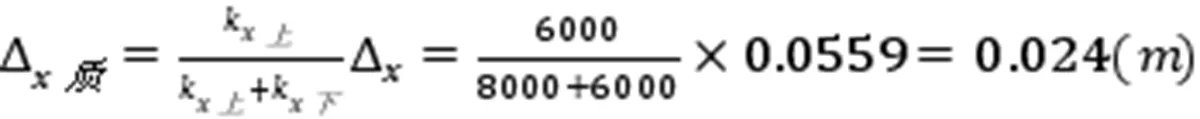
2. 倒撵猴

倒撵猴的旋见图19。由文献[3]的公式的计算，得出表2。

图19倒撵猴的旋

表2 倒撵猴的旋转临界力矩计算

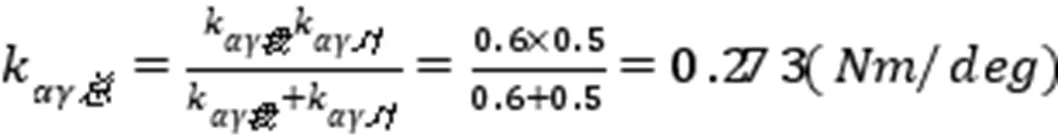
由(18)式第四和六式得总的角变位，

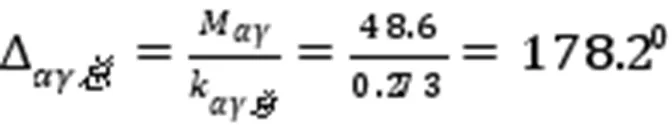
由(20)式第四和六式用于我方接手处变位范围是，

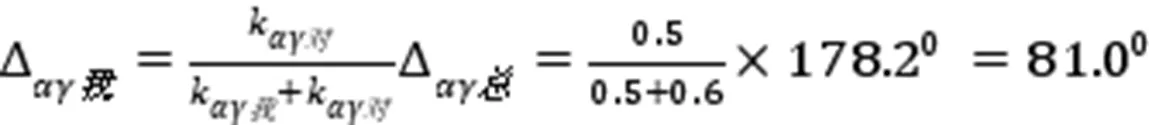
由(20)式第四和六式用于对方接手处变位范围是，

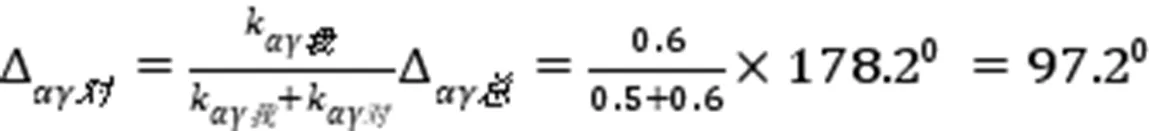
图20攻方要让对方达到极限

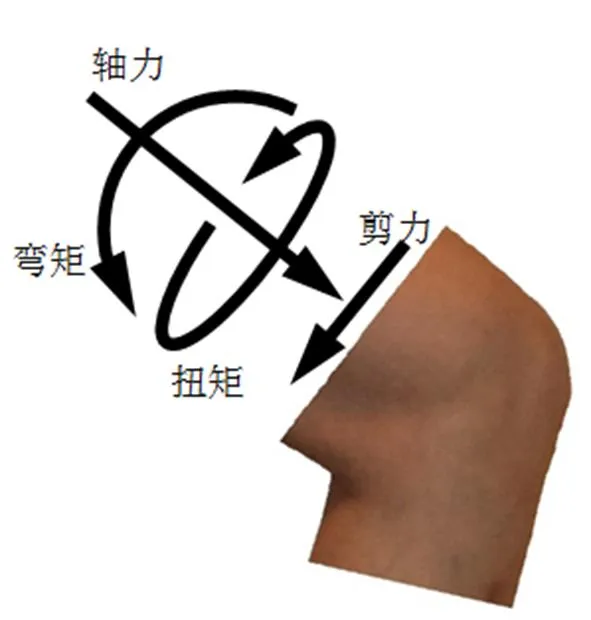
图21 膝关节内力

七、太极拳弹性力学中量的分析方法

弹性系数可以通过实测来得到，当然因有好多种功架，实测的工作量可能很大。弹性系数还和接触状况有关，这样就有更多的组合需要测量。弹性系数也可以通过计算求得。可以将肢体简化成弹性材料，根据几何尺度、功架形状、接触状况来计算。也可以用有限元方法来计算弹性系数。

根据求得的接触力、人体重力、地面对人体的正压力和摩擦力可以计算肢体的内力。内力有轴力、剪力、弯矩和扭矩，见图21。进一步可以计算内应力，内应力有正应力和剪应力。

还可以计算变形。功架的各点的变形可以算出，因而可求得功架形状的变形。可以计算应变，应变有正应变和剪应变。

本文的模型用了准静态的概念，即动态的过程平稳而没有振动。真正的动态过程在理论上是可以模拟的。

今后的工作可以用有限元分析推手的动力学过程。建立两方联合体的隔离体，定出接手处的连接条件，定出各方和支撑面的边界条件。对联合隔建立弹性或粘弹体的有限元。建立人体的支撑动量、整体动量、相对动量的有限元模型。根据失根和打滑条件分析该动态模型，解算出那方得胜及其临界广义力。计算各方的变位、变形、应力应变。计算反关节运动的限制。

[1]顾杰.太极拳弹簧功[J].太极，2013(2,3,4,5,6).

[2]顾杰，郭振兴，卢建辉.太极拳力学[M]. 北京：北京理工大学出版社，2016.

[3]顾杰，恩杰，郭振兴. 用多力的立体模型分析太极拳的静态和动态攻防功能[J]. 邯郸学院学报，2017(1).

（责任编辑：苏红霞 校对：李俊丹）

G852.11

A

1673-2030(2017)04-0070-11

2017-09-10

顾杰（1955—），男，江苏苏州人，邯郸学院太极文化学院客座教授，美国通用汽车公司高级工程师，美国奥克兰大学机械制造博士；郭振兴（1950—），男，河北邯郸人，邯郸学院太极文化学院原院长，高级政工师。