基于非下采样剪切波变换域三变量模型图像去噪算法

石满红，刘 卫



基于非下采样剪切波变换域三变量模型图像去噪算法

石满红1，刘 卫2

（1. 安徽科技学院信息与网络工程学院 安徽 凤阳 233100；2. 中国科学院合肥智能机械研究所 安徽 合肥 230031）

结合非下采样剪切波变换域三变量阈值滤波和多分辨引导滤波，本文提出一种去除高斯白噪声的图像去噪的有效方法。在非下采样剪切波变换域中，以三变量非高斯模型对方向带通子带系数间相关性进行建模，采用最大后验估计理论推导出三变量收缩阈值函数。此外，对低频子带系数采用多分辨引导滤波进行平滑处理，以达到更好的噪声抑制效果。实验结果显示，本文所提去噪方法可以有效抑制噪声同时保留更多的图像细节信息，与其他滤波算法相比，该去噪算法可得到更高的客观数据及更好的视觉效果。

图像去噪；非下采样剪切波变换；三变量非高斯模型；引导滤波

0 引言

图像在其获取与传递过程中，常常会受到各种噪声（如加性高斯白噪声）的污染。图像去噪的主要目的是有效减少噪声等级且保留尽可能多的细节特征。

从处理域的角度，去噪算法可分为空间域滤波和变换域滤波。近年来，学者们提出了很多基于空间域的滤波算法：非局部均值滤波、双边滤波、引导滤波等[1-3]。空间域滤波直接处理图像像素，具有执行速度快，方法简单等优点，但是图像细节信息却无法被提取出来，去噪后图像丢失了很多细节信息、边缘处模糊不清。小波变换凭借其较好的时频局部化能力，可以有效地提取图像的细节信息，因而被广泛的应用在图像去噪领域。针对小波系数之间的强相关性，学者们提出了很多先验统计模型对小波系数进行建模[4-9]，然而这些先验模型存在着对系数间相关性考虑不充分或者估计模型参数过于复杂的问题。

小波变换虽然可以对点奇异分段光滑函数进行最优逼近，但是由一维小波张量形成的二维可分离小波只有有限方向，它们不能很好地表示自然图像的高维奇异特征（边缘、纹理等）。为了更加有效、稀疏的表示图像，多尺度几何分析工具被提了出来，如Curvelet、Ridgelet、Contourlet等[10-12]。随后，学者们提出了很多基于多尺度几何分析的图像去噪算法并取得了较为理想的去噪效果[13-15]。2007年，Guo提出了新的多尺度几何分析工具——Shearlet[16]，理论上可以执行任意多方向的图像分解，逆合成过程具有较高的执行效率，可近似最优地逼近图像。因Shearlet具有这些优点，它在图像处理领域有诸多应用[17-19]。但是，Shearlet变换不具有平移不变性，去噪结果会出现伪吉布斯现象。2008年，Easley提出了非下采样Shearlet变换[20]，它继承了Shearlet变换所有优良特性且具有平移不变性，它更适用于图像去噪工作。

传统的基于变换域去噪算法，大多认为噪声只集中存在于高频子带，低频子带不需要处理。然而，低频子带中也存在一定量的噪声，因此，在执行图像去噪工作时有必要对低频子带也进行相应的处理。基于以上分析，本文提出一种新的图像去噪算法——通过结合非下采样Shearlet变换域的阈值滤波方法和引导滤波方法，达到去除噪声的目的。图像经非下采样Shearlet变换分解后，高频子带运用三变量阈值函数进行处理，对于每次重构得到的低频子带再运用引导滤波平滑处理，图1为本文去噪算法的流程图，其中H0、H1分别为低通和高通分解滤波器，G0、G1为合成滤波器，SF为剪切滤波器，图1中只进行了两层分解，具体应用时可推广到更多层分解。

1 Shearlet变换

Guo等人在合成小波理论基础上衍生出Shearlet变换[16]。定义具有合成膨胀仿射系统为：

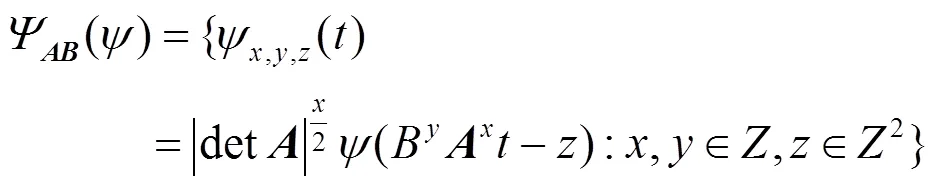
任意Î＋，Î，Î2，Shearlet基函数定义为：

基于以上Shearlet定义，函数()的Shearlet变换为：

SH(,,)＝<,,,> (2)

式中：、s、分别表示尺度参数、剪切的方向以及平移量。图2显示了Shearlet的频域支撑。

非下采样Shearlet变换分多尺度剖分与方向局部化两步执行。在多尺度剖分阶段，为了使其具有平移不变性、抑制图像处理结果出现的伪Gibbs现象，在实现过程中去除了下采样操作，采用非下采样金字塔滤波器组进行多尺度分解；在方向局部化阶段，采用平移不变剪切滤波器组将频域分解为一系列的梯形高频子带。更多关于非下采样Shearlet变换的内容，可以参考文献[20]。

2 引导滤波

引导滤波[3]是一个局部线性平移不变的边缘保持滤波器，它基于两个假定条件的折中，第一个条件是引导图像和滤波结果图像之间存在线性模型，第二个条件是滤波结果应该尽可能的与源图像相似。对于像素的滤波结果为：

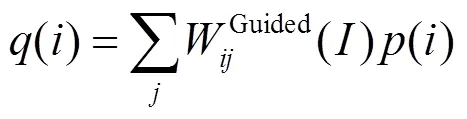
式中：WijGuided(×)表示引导图像I的滤波核函数且与源图像p相互独立。

图2 Shearlet变换频域支撑

式(3)的滤波核函数定义为：

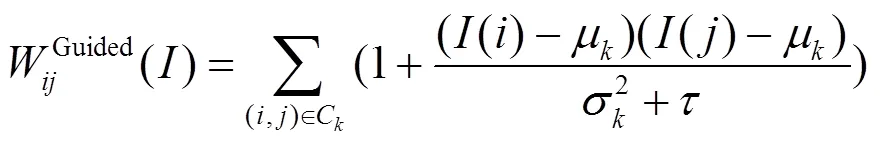
式中：和2分别表示引导图像局部窗口c的均值和方差；＞0防止分母为零。

3 NSST域三变量统计模型

对于受到零均值加性高斯白噪声污染的原始图像，其退化模型为：

(,)＝(,)＋(,) (5)

式中：(,)、(,)、(,)分别代表原始图像、噪声图像及高斯白噪声（方差为2）。图像经过NSST变换后，得到：

＝＋(6)

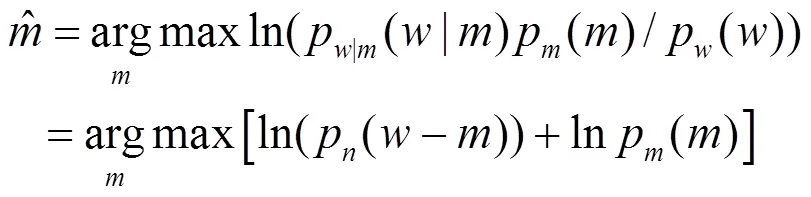
对于式(8)，我们需要得到噪声的概率密度函数p()与图像的NSST系数的概率密度函数p()。文中处理的对象是高斯白噪声，即～(0,2)，其中2为噪声的方差。然而我们无法准确获得p()，通常做法是使用一个相近的概率密度函数作为替代。图3(c)、(d)为自然图像Lena和红外图像Plane的最细子带的概率直方图，所有的分布都在零值附近具有一个非常尖锐的顶峰且在峰值两边有着很长的拖尾现象，这些结果显示了NSST系数是极度稀疏的，大部分的系数幅值都在零值左右。相似的情况也出现在其他图像中，因此图像的NSST系数具有非常高的非高斯性。

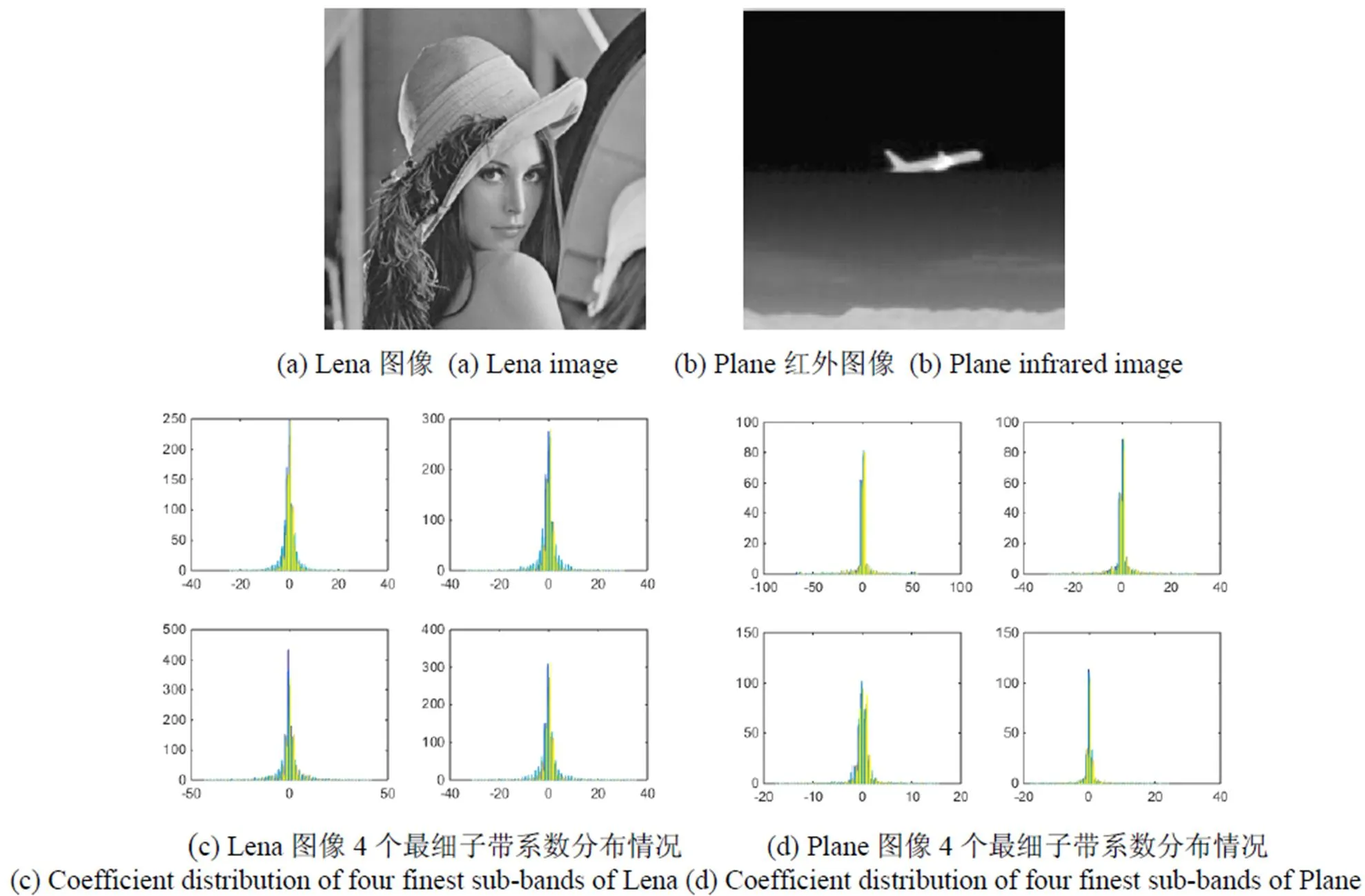
图3 NSST最细子带系数统计直方图

3.1 NSST系数间的依赖关系

由前面分析可知，NSST高频子带系数的分布情况呈现出零均值、重拖尾的特点，HMT[5]、GGD[6]等模型都可近似其边缘概率分布。但这些模型大多只反映系数尺度间或尺度内相关性，无法充分体现NSST系数间相关性。为了定量分析系数间的依赖关系，本文使用互信息[21]作为量化指标来度量NSST系数间的依赖关系。两个具有边缘概率密度函数()、()及联合概率密度函数(,)的随机变量、的互信息定义为：

互信息MI(X;Y)表示用Y表示X的信息量，其值越大说明两者关系越紧密，当变量X、Y相互独立时，MI(X;Y)等于0。下面我们使用(9)式计算NSST系数间的互信息值，令m表示当前的NSST系数，Pm表示其父系数，Nm表示邻域系数，Cm表示兄弟系数，图4为一幅图像经3层NSST分解（方向分别为1、4、16），系数间相关的相互关系。

首先，我们对4幅标准图像（Lena, Barbara, Boat, Peppers）、2幅红外图像以及2幅遥感图像进行NSST分解（尺度数3），然后在最细方向子带上分别计算MI(;)、MI(;)、MI(;,)以及MI(;,)的平均互信息值，表1给出计算结果。

从表1可知，平均互信息值满足不等式MI(;)＜MI(;)＜MI(;,)＜MI(;,)，即(,)可以提供给的信息量要远远高于或者。因而，为了捕获NSST系数间相关性，充分描述当前系数与父系数和兄弟系数间相关性，文中使用三变量分布模型进行建模。

3.2 基于NSST域三变量统计模型图像的去噪

设1、2、3是干净的NSST的系数，且2是1的父系数，3是1相反方向兄弟系数。1、2、3为当前观测到含噪NSST系数，1、2、3为高斯白噪声的变换系数。则有：

即：＝＋，其中＝(1,2,3)，＝(1,2,3)，＝(1,2,3)。

假定噪声服从高斯分布，从而它的概率密度函数为：

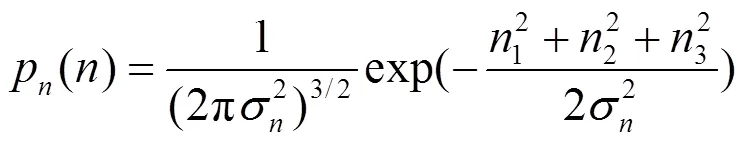
通过以上分析，本文使用三变量广义球等高指数作为当前系数、父系数和兄弟系数的概率密度函数，即：

式(12)是一个概率密度函数且具有对称性，它充分显示1、2和3之间的相关特性，其中是一个自由参数，在处理图像过程中通常取为值为3，2为NSST系数方差，2为噪声方差。

令()＝ln[p()]，则(7)等价于：

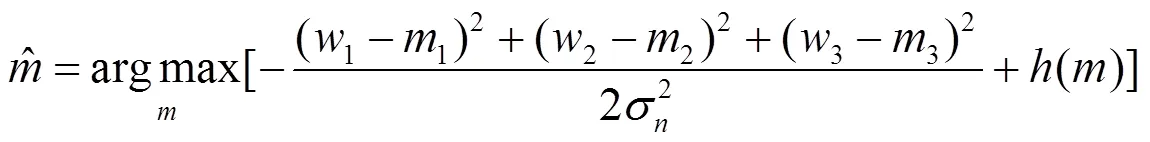
表1 NSST系数的平均互信息值（最细子带）

由于()函数是可微的、严格凸的，对式(13)关于1、2及3求导。然后将式(12)代入式(13)，有：

整理得：

将(15)代入方程组(14)，有：

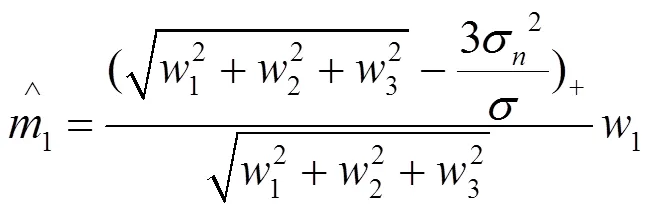
4 算法主要步骤

4.1 参数估计

式中：2()是系数w对应的噪声方差；()是以w为中心的方形邻域；2为()中的系数。

4.2 去噪主要步骤

本文去噪方法主要步骤总结如下：

Step 1 对含噪图像进行NSST分解（尺度数4，方向数4、8、8、16），得到NSST系数；

Step 2 采用蒙特卡罗方法估计2，再用式(17)估计2；

Step 4 对逆NSST变换中的每层低频子带采用引导滤波进行平滑处理，从而得到最终的去噪图像。

5 实验结果与分析

为了验证本文所提去噪算法在去除加性高斯白噪声时的可行性和有效性，我们分别对自然图像（Lena、Barbara）、红外图像（Plane）及遥感图像（Pentagon）进行测试，加入均值为零、方差为2的高斯白噪声。在仿真的实验中，比较本文所提去噪算法与几种较为优秀的去噪算法：LAWML[22]，NSCT[23]、BiShrink[7]、SURE-LET[24]以及KSVD[25]；然后使用两个常用的客观指标（峰值信噪比（PSNR）、平均结构相似性[26]（MSSIM））结合去噪图像的视觉效果来综合评价各个方法的有效性，图5～图8和表2～表3为本文的实验结果。

表2 不同图像去噪后峰值的信噪比（PSNR/dB）

图5～图8为使用不同去噪方法处理含高斯噪声标准差为20的自然图像（Lena、Barbara）、红外图像（Plane）及遥感图像（Pentagon）得到的去噪结果图。尽管没有明确的客观方式用于判别去噪图像的视觉效果，但是通常会使用两个重要的准则：人工纹理信息感知度与图像边缘信息保留度。从图中可以看出，与其他几种去噪方法相比，本文方法表现出更加优秀的抑制噪声的性能，去噪图像的视觉效果更好。在平坦区域，图像表面更加平滑；在纹理丰富区域，保留了更清晰的边界信息。虽然各个去噪图像中都有一定量的人工纹理信息存在，但是本文方法的去噪结果图中出现的人工纹理是最少的。

从表2可以看出，PSNR值随着噪声方差的增加呈下降的趋势。对不同含噪的图像，较之其他的方法，本文方法均得到最大PSNR值。相比较于LAWML、SURE-LET算法，所提方法的PSNR值有较大幅度的提高，特别对于红外图像Plane和遥感图像Pentagon，本文方法获得的PSNR值的优势较为明显；与其余几种优秀的去噪方法相比，PSNR值也都有一定程度的提高，这主要归功于NSST变换可以更加稀疏地表示图像、三变量模型可以准确地对系数尺度内和尺度间相关性进行建模以及对重建的低频系数进行边缘保持滤波，这些有效策略都为更好地抑制噪声做出贡献。

表3 不同方法对不同图像去噪后的平均结构相似性（MSSIM）

图5 方差为20的图像（Lena）去噪后局部放大图

MSSIM值可以评估去噪算法保留边缘纹理信息的能力，因此我们在实验中也使用了MSSIM作为客观度量。各个方法处理不同等级噪声图像得到的客观数据如表3所示。从表3中我们不难看出，本文方法的去噪图像MSSIM值最高，这意味着所提方法保持原图像结构的能力最好。

6 结论

如何精确度量NSST系数间相关性是基于变换域贝叶斯去噪方法的核心问题之一。为了充分反映NSST系数之间的相关性，首先使用三变量广义球等高指数对当前系数、父系数及兄弟系数进行建模，在此基础上，推导出系数估计函数，最后对逆变换过程中的低频子带系数进行引导滤波平滑处理，从而得到最终的去噪图像。仿真实验显示出本文所提去噪算法不仅使得高斯白噪声被有效去除而且去噪图像中带来了更少的人工纹理信息，较之当前几种优秀算法，本文算法在客观度量及视觉效果上均获得了更为理想的结果。

图6 噪声方差为20的图像（Barbara）去噪后局部放大图

图7 不同方法去噪后的红外图像（Plane）比较（噪声标准差为20）

图8 不同方法去噪后的遥感图像（Pentagon）比较（噪声标准差为20）

[1] Buades A, Coll B, Morel J M. A non-local algorithm for image denoising[C]//, San Diego: 2005, 2: 60-65.

[2] Chaudhury K N. Acceleration of the shiftable O(1) algorithm for bilateral filtering and non-local means[J]., 2013, 22(4): 1291-1300.

[3] HE K, SUN J, TANG X. Guided Image Filtering[C]//, 2010, 35(6): 1-14.

[4] DONOHO D L. Denoising by soft-thresholding[J]., 1995, 41(3): 613-627.

[5] CROUSE M S, NOWAK R D, BARANIUK R G. Wavelet-based statistical signal processing using hidden Markov models[J]., 1998, 46(4): 886-902.

[6] CHANG S, YU B, Vetterli M. Adaptive wavelet thresholding for image denoising and compression[J]., 2000, 9(9): 1532-1546.

[7] SENDER L, Ivan W. Selesnick. Bivariate Shrinkage Functions for wavelet-based denoising exploiting interscale dependency[J]., 2002, 20(11): 2744-2756.

[8] Portilla J, Strla V. Image denoising using scale mixtures of Gaussians in the wavelet domain[J]., 2003, 12(11): 1338-1351.

[9] CHO D, BUI T D. Multivariate statistical modeling for image denoising using wavelet transforms[J]., 2005, 20(1): 77-89.

[10] Candes E. Ridgelets: Theory and Applications[D]. USA: Department of Statistics, Stanford University, 1998.

[11] Starck J L, Candes E J, Donoho D L. The curvelet transform for image denoising[J]., 2002, 21(11): 131-141.

[12] DO M N, VETTERLI M. The Contourlet transform: an efficient directional multiresolution image representation[J]., 2005, 14(12): 2091-2106.

[13] 贾建, 焦李成, 项海林. 基于双变量阈值的非下采样Contourlet变换图像去噪[J]. 电子与信息学报, 2009, 31(3): 532-536.

JIA Jian, JIAO Licheng, XIANG Hailin. Using bivariate threshold function for image denoising in NSCT domain[J]., 2009, 31(3): 532-536.

[14] YANG H Y, WANG X Y, QU T X, et al. Image denoising using bilateral filter and Gaussian scale mixtures in shiftable complex directional pyramid domain[J]., 2011, 37(5): 656-668.

[15] Ramin E, Hayder R. Translation-invariant contourlet transform and its application to image denoising[J]., 2006, 15(11): 3362-3374.

[16] GUO K, Labate D. Optimally sparse multidimensional representations using shearlets[J]., 2007, 39(1): 298-318.

[17] YI S, Labate D, Easley G R, et al. A shearlet approach to edge analysis and detection[J]., 2009, 18(5): 929-941.

[18] 朱华生, 徐晨光. Shearlet变换域自适应图像去噪算法[J]. 激光与红外, 2012, 42(7): 811-814.

ZHU Huasheng, XU chenguang. Adaptive image denoising algorithm based on Shearlet transform[J]., 2012, 42(7): 811-814.

[19] Deng C, Wang S, Chen X. Remote sensing images fusion algorithm based on shearlet transform[C]//, WuHan: 2009: 451-454.

[20] Easley G, Labate D, Lim W Q. Sparse directional image representations using the discrete shearlet transform[J]., 2008, 25(1): 25-46.

[21] LIU J, Moulin P. Information-theoretic analysis of interscale and intrascale dependencies between image wavelet coefficients[J]. I, 2001, 10(11): 1647-1658.

[22] Mihcak M K, Kozintsev I, Ramchandran K. Low-complexity image denoising based on statistical modeling of wavelet coefcients[J]., 1999, 6(12): 300-303.

[23] Cunha A L, Zhou Jianping, Do M N. The nonsubsampled contourlet transform: theory, design and application[J]., 2006, 15(10): 3089-3101.

[24] Luisier F, Blu T, Unser M. A new SURE approach to image denoising: interscale orthonormal wavelet thresholding[J]., 2007, 16(3): 593-606.

[25] MICHAEL E. Image denoising via sparse and redundant representations over learned dictionaries[J]., 2006, 15(12): 3736-3745.

[26] ZHOU W, Bovik A C, et al. Image quality assessment: from error visibility to structural similarity[J]., 2004, 13(4): 600-612.

Image Denoising Using a Trivariate Model in the Nonsubsampled Shearlet Transform Domain

SHI Manhong1，LIU Wei2

(1.,,233100,; 2.,,230031,)

We present an efficient algorithm for removing white Gaussian noise from corrupted images by incorporating a nonsubsampled Shearlet transform (NSST)-based trivariate shrinkage filter into a multiresolution guide filter. In the NSST domain, coefficients are modeled as a trivariate Gaussian distribution, accounting for the statistical dependencies among interscale and intrascale transform coefficients. A nonlinear trivariate shrinkage function is derived using a maximum a posteriori (MAP) estimator. To obtain better denoising results, low-frequency sub-bands are smoothed using a multiresolution guide filter. Experimental results show that our algorithm is very effective in eliminating image noise, and performs better than other denoising techniques.

image denoising，nonsubsampled Shearlet transform，trivariate non Gaussian model，guided filter

TN911. 73

A

1001-8891(2017)11-1045-09

2017-04-21；

2017-07-29.

石满红（1987-），女（汉族），安徽安庆人，助教，硕士，研究方向计算机辅助几何设计。

安徽科技学院校级项目（ZRC2016499），安徽省自然基金资助项目（1508085MC55），安徽省教育厅自然科学重点项目（KJ2016A174）。