例谈在数学课堂中“自学互帮”

江超

夸美纽斯曾说过：“要寻找出一种有效的数学方法，使教师少教，给学生多学。”随着以“自学互帮”为核心理念的课改的推行，深感收益之时，也坚信学生也必将是一生多学，我把运用该理念指导教学的两个片段写下来，与大家共勉，以求抛砖引玉之效。

片段1：《角平分线的性质探究》

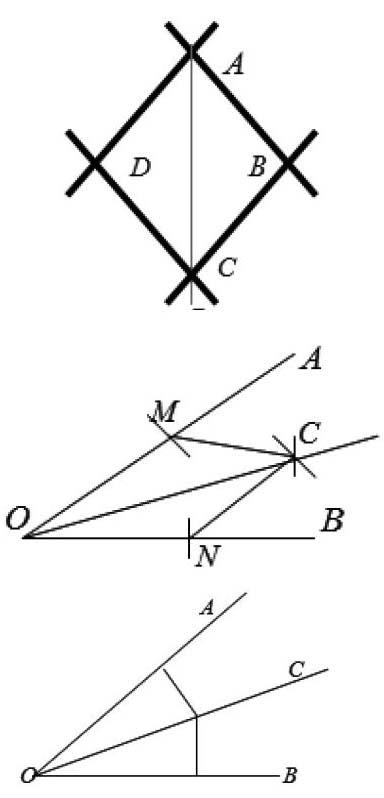
教具准备：用硬纸条、红毛线自制右图。

学具准备：刻度尺、白纸、铅笔等。

【教师活动1】展示自制教具，让学生观察红毛线与上面两纸条形成的夹角的关系。

（评析：用直观教具引入，提高了学生的学习兴趣。）

【学生活动1】观察老师展示的教具，把结果写在草稿纸上。

（学情分析：此前几节课研究了全等三角形，学生比较容易看出有两个三角形全等，并且在此基础上，我用手有意提醒学生观察拉线与相邻纸条形成的夹角大小关系。由于有全等的基础，因此较易得到相等的结论。教师在引导学生观察，无论角度大小怎样改变，拉线都能平分夹角，因此，我们把这个工具可以称为简易角平分仪器。）

【学生活动2】

（1）想一想，仿照角平分仪器的结构，用尺规怎样来画角平分线呢？

（2）尝试用直尺、圆规画∠AOB的平分线。

（3）自学教材，领会右图的构建方法。

（4）正确用直尺、圆规画∠AOB的平分线。

（评析：合理利用教材，组织学生自学。）

【教师活动2】为什么要以大于的长为半径画弧？试一试以等于或者小于的长为半径画弧能找到C点吗？

（评析：突破教材知识中的难点，选择时机恰当。充分体现了教师的“导”，并把握好教师导的角度。）

【学生活动3】继续尝试后面两种情况下画角的平分线。和同学交流你作图的结果，尝试总结三种情况画图的结果。

【教师活动3】根据观察找两个有代表性的同学发言。并且肯定：以大于 的长为半径画弧一定能够找到C点；以小于 的长为半径画弧找不到C点；以等于 的长为半径画弧有时能够找到C点，有时却找不到，这主要取决于画图的准确性。结论：按教材上讲的方法进行较好。

【学生活动4】猜一猜，平角的角平分线与平角的边的位置关系如何？再画图验证。

【教师活动4】引导学生由此得到过直线上的一点，画这条直线的垂线的方法。

（评析：知识的延伸，思维的拓宽，在较少的时间获得较多知识，以突出教学的有效性。）

【学生活动5】请同学们在一张白纸上画∠AOB，两人为一组再设计一种画∠AOB的平分线的方法。教师及时发现并推广折叠的方法画角的平分线：折叠使角的两边重合，从角的顶点出发，在角的内部沿折痕画一条射线，便得到角的平分线。

（评析：合作互帮，共享成果。学会把复杂的事情简单处理。提高学生解决问题的能力和兴趣。）

【学生活动6】请同学们在这条角平分线上任取一点，向角的两边做距离。并且观察这两个距离的大小关系。最好能想办法验证。希望同学们四人一组合作完成。

【教师活动5】引导学生进行总结。

验证方法一：折叠，两个距离能完全重合。因此，这两个距离是相等的。

验证方法二：这个图的两个直角三角形，利用角角边容易证明是全等的。因此，这两个距离相等。

【教师活动6】先让同学们七嘴八舌总结出角平分线定理，只要有角平分线，这条线上的一点到角的两边的距离相等就行。鼓励同学们来探究命题证明的三部曲。

再让同学们来证明。要证明，就得有图形，已知条件，求证。引导学生先根据命题画出图形，再结合命题的题设写出已知条件，由结论部分写出求证。最后进行证明，并且得出角平分线定理。

（评析：这是实验的升华，实验的结果是否正確，用学会的方法加以论证，并且是正确的话，可以作为定理，成为其他命题的推理依据。培养学生的可持续发展观。）

【学生活动7】仿照角平分线性质定理的证明方法和研究，完成角平分线的判定定理的证明。

【学生活动8】在学生具备这些知识后，立即进行巩固练习，教材练习：找图上的建筑设计位置。鼓励学生用两种画角平分线的方法找到位置。对用折叠方法找到位置的同学给予正确的肯定。

（评析：这节课是教师在积极调动引导学生自主探索，证明，并且合作交流完成了学习任务。充分体现了自学互帮的教学理念。）

片段2：《全等三角形的判定、性质习题课》

【学生活动1】总结全等三角形的判定方法。首先，每个同学独立写在草稿本上，然后查阅资料矫正，最后同桌同学交换检查。

【教师活动1】注意巡视同学们练习的进展情况，以便及时发出下一个环节的指令。

（评析：因为全等三角形的四个判定方法在教材上很容易找到，就是有个别懒惰的不写完，所以要求学生之间互相检查督促。这是独立学习与合作学习的结合。）

【学生活动2】知道两个三角形全等后，可以得到哪些结论？也就是全等三角形的性质有哪些？要求与活动1相同。

【教师活动2】注意巡视同学们练习的进展情况，以便及时发出下一个环节的指令。

（评析：因为全等三角形的性质在这一章没作总结，所以较多学生不知道全等三角形的用处，我在巡视的时候特别留意学生总结的情况，让同学们在与同桌交流后，还与周围的同学继续交流，并且在此基础上，组织了全班同学进行交流。

在交流中，同学们除了总结出全等三角形的对应边、对应角相等之外，还发现了两个全等三角形的周长、面积也相等，甚至还有同学发现在两个全等三角形的对应位置画的线段也是相等的。这完全是一个意外生成：我在教学三角形全等时，让每个同学用白纸剪了一对全等三角形，并且让同学们把它夹在书里，复习总结时把它拿在手上看到来说或者写，有个学生夹得时候不小心，把三角形折了，于是就产生了两个全等三角形的对应位置画的线段一样的折痕，也就有了这个结论。这时我就因势利导，对应位置画的线段不方便研究，建议大家找一些特殊的线段来研究，这就引来全等三角形的对应角平分线、中线、高相等。并且我还进一步引导同学们把结论：全等三角形的对应角平分线、中线、高相等作为定理进行了证明。）

【学生活动3】证明：全等三角形的对应角平分线、中线、高相等。

练习要求：三人为一个学习小组，每个同学各选三条线段中的一条进行证明。然后交流检查。

（评析：这三个性质的证明，既巩固了全等三角形的判定方法，又学习巩固了全等三角形的性质。同时学生对自己的发现来加以证明热情很高，这节课的效果可见是很好的。）

总之，我们在运用自学互帮的思想指导教学时，并非是八股论调，一成不变，而是通过教师去播下那粒种子，学生去把它变成森林。