驻波的瞬时能流密度

章 文 张 玉 张子云 衡太骅

(安徽大学 1物理与材料科学学院； 2生命科学学院，安徽 合肥 230601)

驻波的瞬时能流密度

章 文1张 玉2张子云1衡太骅1

(安徽大学1物理与材料科学学院；2生命科学学院，安徽 合肥 230601)

本文首先指出了人们利用瞬时能流密度解释驻波能量的认识误区。之后论证了两列简谐波在相遇区域任一点的瞬时能流密度等于两列波各自的瞬时能流密度之和的条件是两列波必须相向传播，从而严格证明了驻波瞬时能流密度的结论。最后从受力的角度分析了驻波的能量只能在相邻波腹和波节间流动。

驻波；瞬时能流密度；叠加原理

驻波是振幅相同的两列相干简谐波，沿同一直线相向传播时，在相遇区域内形成的一种特殊的干涉现象。关于驻波的能量流动，多数大学物理教材仅简单介绍了结论，而解释得不够透彻。目前已有部分文献分别用图示法[1,2]和解析法[3-5]探讨了驻波的能量流动问题。关于驻波能量的解析，人们将两列相干简谐波的瞬时能流密度相加得到驻波的瞬时能流密度[3]，并依此分析驻波能量的传播规律。然而，这种方法虽能正确地解释驻波能量的流动，却容易使读者对瞬时能流密度的认识产生一定的误区，即两列简谐波叠加时波线上任一点的瞬时能流密度一定等于两列波各自的瞬时能流密度之和。这种理解正确与否还需要从理论上严格论证。本文首先讨论了上述问题并严格证明了驻波的瞬时能流密度等于入射波和反射波瞬时能流密度之和。之后定性分析了驻波的波腹和波节处没有能量传播的原因。

1 瞬时能流密度的认识误区

1.1 文献[3]中驻波瞬时能流密度的推导

设形成驻波的入射波和反射波(沿x轴方向传播)的波函数分别为

式中,ρ为介质的密度，负号表示瞬时能流密度沿x轴负方向。故驻波瞬时能流密度的大小为

I12=I1+I2=-uρω2A2sin2ωtsin2kx

(5)

1.2 能流密度的认识误区

文献[3]中驻波瞬时能流密度的推导直接运用了I12=I1+I2这个结论，这会让我们对瞬时能流密度的认识产生一定的偏差。从后面2.2节的论证就能看出I12=I1+I2这个结论并不总是成立。众所周知，能流密度是矢量。通常一个物理量能被定义为矢量需满足两个条件，一是该物理量有大小有方向，二是两个物理量的加法满足平行四边形法则，例如力F、速度、电场强度E等。但对于瞬时能流密度，其加法是否与矢量的加法相同？因为在两列(或多列)波相遇时需满足波的叠加原理。波的叠加原理仅能保证在相遇区域内，任一质元振动的位移是各列波单独存在时在该点引起位移的矢量和。而由此并不一定能推出总的瞬时能流密度等于两列波各自的瞬时能流密度之和，所以需从波的叠加原理严格证明1.1中式(5)的结论。

2 两列简谐波相遇区域内的瞬时能流密度

2.1 瞬时能流密度的普适公式

(6)

运用式(6)亦可得出式(3,4)的结果。

2.2 两列简谐波相遇区域内的瞬时能流密度

本小节以沿x轴传播的两列简谐波为例来说明总的能流密度不一定等于两列波的能流密度之和。设沿x轴传播的两列简谐波的波函数分别为

式(7,8)中k和k′前的正负号分别对应简谐波沿x轴负向和正向传播。则由式(6)可知，两列简谐波的瞬时能流密度分别为

(9)

根据波的叠加原理可得两列波的合成为y34=y3+y4，因此从式(6)可得两列波在相遇区域内的瞬时能流密度为

(10)

式中

(11)

式(11)中的I′是两列波的叠加项。从式(9-11)可明显看出，当且仅当式(10)中的叠加项I′=0时才有I34=I3+I4成立。将式(7,8)代入式(11)可得

(12)

2.3 讨论

从式(7,8,12)可以看出：

1) 若两列简谐波都沿x轴正向传播，且ωt-kx+φ=nπ或ω′t-k′x+φ′=nπ时，有I′=0，从而I34=I3+I4；

2) 若两列简谐波都沿x轴正向传播，但ωt-kx+φ≠nπ，且ω′t-k′x+φ′≠nπ时，I′≠0，从而I34≠I3+I4；

3) 当两列简谐波都沿x轴负向传播时，经过相同的计算也可得出与1)和2)类似的结论；

4) 而当两列简谐波相向传播时，始终会有叠加项I′=0成立，从而I34=I3+I4；

5) 驻波不仅满足4)中的条件，而且还需要满足A=A′，ω=ω′ 以及k=k′。所以对于驻波而言，总的瞬时能流密度等于入射波和反射波各自的瞬时能流密度之和。

从1)和2)可看出，对于特定时刻只有一些特殊的点I34=I3+I4，对于波线上任一特定的点，只在某些特殊的时刻有I34=I3+I4。至此，我们不仅严格证明了式(5)，而且还得出结论，即当且仅当两列任意的简谐波相向传播时，波线上任一点的瞬时能流密度始终等于两列波各自的瞬时能流密度之和。

利用式(5)可清楚地分析出驻波中的能量仅在相邻的波腹和波节间流动。具体的分析见文献[3]。下一节我们将从受力的角度定性解释驻波能量流动的特点。

3 驻波能量流动的定性解释

考虑式(1)和式(2)中两列简谐波形成的驻波。驻波方程为

y-{12}=y1+y2=2Acosωtcoskx

(13)

驻波的波形见图1。

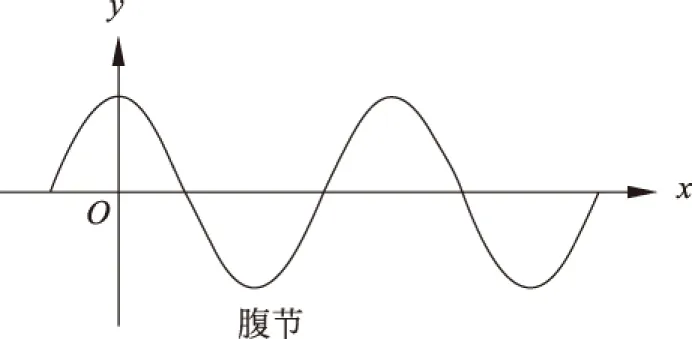
图1 驻波波形

腹左边的介质对右边的介质没有力的作用，因而波腹处不存在能量的传播。波节处有形变，但从对称性(见图1)可知任意时刻波节左边介质和右边介质对波节的作用力始终大小相等而方向相反，同时波节永远是静止的，因此波节处也没有能量的传播。所以驻波的能量只能在相邻的波节和波腹间流动。驻波动能和势能间的转化见文献[4]。

4 结语

本文指出了人们对瞬时能流密度的认识误区，证明了任意两列波相遇区域的瞬时能流密度不一定等于两列波各自的瞬时能流密度之和。最后从受力的角度定性解释了驻波能量只能在相邻波节和波腹间流动的原因。

[1] 吴颖,谢远亮.关于驻波能量的图示法分析[J].沈阳航空工业学院学报,2007,24(1):84-86. Wu Ying, Xie Yuanliang. Illustration analysis of standing wave energy[J]. Journal of Shenyang Institute of Aeronautical Engineering, 2007, 24(1): 84-86. (in Chinese)

[2] 卢艳,董慎行.用计算机模拟驻波能量的变化[J].物理与工程,2003,13(4):47-49. Lu Yan, Dong Shenxing. Imitating the energy variety of standing wave[J]. Physics and Engineering, 2003, 13(4): 47-49. (in Chinese)

[3] 郭建军.关于驻波能量的分析[J].大学物理,2005,24(5):23-25. Guo Jianjun. An analysis of the energy of standing wave[J]. College Physics, 2005, 24(5): 23-25. (in Chinese)

[4] 李平.驻波的能量[J].大学物理,1995,14(6):46-47. Li Ping. Energy of standing wave[J]. College Physics, 1995, 14(6): 46-47. (in Chinese)

[5] 蒋练军,李木林.驻波能量探究[J].湖南理工学院学报:自然科学版.2004,(04):56-58. Jiang Lianjun, Li Mulin. Probe into standing wave energy[J]. Journal of Hunan Institute of Science and Technology(Natural Sciences) , 2004,(04): 56-58. (in Chinese)

■

INSTANTANEOUS ENERGY FLUX DENSITY OF STANDING WAVE

Zhang Wen1Zhang Yu2Zhang Ziyun1Heng Taihua1

(1School of Physics and Materials Science，2School of Life Science, Anhui University, Hefei Anhui 230601)

Firstly, we point out the misunderstanding of people, who use the instantaneous energy flux density to explain the energy of standing wave. Then we strictly prove that the instantaneous energy flux density of two harmonic waves at arbitrary point in the crossed region is equal to the sum of the two corresponding instantaneous energy flux densities if and only if the two waves are travelling oppositely. Thus, the conclusion of instantaneous energy flux density of standing wave is strictly proved. At last, by using the force analysis, we explain the energy of standing wave can only be transited between the adjacent wave loop and wave node.

standing wave; instantaneous energy flux density; superposition principle

2015-10-15；

2016-06-30

安徽大学本科教育质量提升计划项目(xjjyxm14030，ZLTS2015054) ；安徽省省级质量工程项目(2015jyxm051)。

章文，副教授，主要从事大学物理和量子信息方面的教学科研工作,wenzhang@ahu.edu.cn。

章文，张玉，张子云，等. 驻波的瞬时能流密度[J]. 物理与工程，2017，27(1)：44-46.