核磁共振陀螺中内嵌碱金属磁力仪研究

罗 晖,杨开勇,汪之国,张 燚,夏 涛,赵洪常

(国防科技大学光电科学与工程学院,长沙410073)

核磁共振陀螺中内嵌碱金属磁力仪研究

罗 晖,杨开勇,汪之国,张 燚,夏 涛,赵洪常

(国防科技大学光电科学与工程学院,长沙410073)

核磁共振陀螺利用核自旋的闭环磁共振实现角速度的测量,其磁共振信号一般由内嵌碱金属磁力仪测出。为了提高磁力仪性能,对描述磁力仪的Bloch方程,采用微扰迭代法和级数展开法,求出了各磁矩分量的近似解,然后讨论了线性测量范围随纵向与横向弛豫时间的变化规律以及频率响应特性。利用数值仿真,对上述近似解析解进行了验证。结果表明,磁力仪的线性测量范围随纵向、横向弛豫时间的增大而减小,其频率响应为一阶低通,截止频率仅与横向弛豫时间有关。上述研究对核磁共振陀螺的优化有一定的参考意义。

核磁共振陀螺;碱金属磁力仪;线性测量范围;频率响应

0 引言

在现代战争中,从预警机、潜艇等大型武器平台到单兵、微型无人机、无人水下航行器等小型作战单元的战斗效能都极其依赖于导航与定位能力。卫星导航精度高、成本低,但信号易被干扰、存在覆盖盲区以及卫星会受到攻击等问题降低了卫星导航的可靠性[1]。纯自主的惯性导航是最理想的导航方式,它是唯一同时具有自主、实时、连续、隐蔽、不受干扰,无时间、地点、环境限制的导航技术。用于感知载体角运动的陀螺仪是惯性测量装置的核心,决定着惯性技术的发展方向[2]。

近年来,量子技术逐渐实用化,在陀螺领域出现了原子陀螺技术,包括原子干涉陀螺[3-5]、原子自旋陀螺[3,6-7]、核磁共振陀螺等多种类型[8-12]。其中核磁共振陀螺同时具备精度高、体积小、功耗低等优点,目前精度优于0.01(°)/h的核磁共振陀螺除电路外的体积只有10cm3,成为最有发展潜力的导航级陀螺仪。

在典型的核磁共振陀螺中,碱金属蒸气不仅起到自旋交换光泵浦的作用,还用于检测核自旋的进动信号以及对环境磁场的测量[8],因而其特性对核磁共振陀螺的性能具有重要影响。针对核磁共振陀螺中内嵌碱金属磁力仪的工作原理已有详细研究[8],但关于其线性测量范围和频率响应的分析却未见报道,而这两种特性对磁共振信号检测有显著影响。因此,本文采用微扰法,对描述磁力仪运动的Bloch方程进行了近似求解,获得了线性测量范围和频率响应的近似解析式,从而能够更深入地掌握磁力仪的特性,为核磁共振陀螺性能优化提供参考。

1 核磁共振陀螺内嵌碱金属磁力仪基本原理

内嵌碱金属磁力仪所用原子可以为87Rb、85Rb、133Cs等,这里我们以87Rb为例进行分析。87Rb原子磁力仪原理如图1所示[8]:沿z轴的泵浦光用来使87Rb电子自旋极化,z向施加磁场Bz=B0+Bccos(ωct) ,这里B0为恒定磁场,Bc为调制磁场幅度,ωc为调制磁场角频率,t为时间。沿x轴的探测光通过气室后测出87Rb原子极化强度的x分量。 设x和y方向待测磁场分别为Bx和By,下面具体分析87Rb原子自旋磁矩的运动特性。

图1 内嵌碱金属磁力仪原理示意图Fig.1 Schematic diagram of embedded magnetometer

图1中,Rb自旋磁矩的运动可用Bloch方程描述

(1)

式中,Mx、My、Mz分别为87Rb原子自旋磁矩在X、Y、Z轴上的磁化强度分量,τ1为纵向弛豫时间,τ2为横向弛豫时间,γ为87Rb原子的旋磁比,M0为z轴稳态磁化强度。

当ωc≫1/τ2时,磁矩无法响应z向调制磁场,这时将在磁矩中出现各次谐波。

令M+=Mx+iMy,由式(1)得到近似解为

(2)

式中,Jn(β)表示宗量为β的n阶第一类贝塞尔函数,p为整数,β=γBc/ωc。

为了避开低频噪声,取式(2)中ωc的基频,通过锁相放大器取出cosωct和sinωct的幅度,即可得到分别正比于Bx和By的量,从而实现二维矢量磁力仪。实际上,式(2)仅仅为式(1)的一种近似解,并未考虑磁力仪的频率响应,也得不到磁力仪的测量范围,而这些问题将影响磁力仪的实际工作特性。

2 内嵌碱金属磁力仪实际工作特性

2.1 线性测量范围

我们采用微扰迭代法来对式(1)的Bloch方程进行求解[13]。

设待测磁场沿x轴,由式(1)中的前两式得

(3)

式(1)中第三式成为

(4)

(5)

(6)

当ωc≫1/τ2时, 式(6)求和号中只有n=-1的一项较大,其他项可以忽略,得到1阶解

(7)

(8)

[J0(β)-J2(β)]sinωct

通过对在校生不同年级的统计得出如下结果。从表1中可以看出，三年级的各维度和总得分情况均高于其它年级，而一年级的各项得分普遍低于其他年级。

(9)

2.2 频率响应

(10)

式中

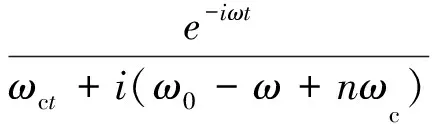
ωct=1/τ2。

当ωct≪ωc且ω较小时,式中共振项起主要作用,式(10)可近似为

M+= -iMzγB1J1(β)[J2(β)eiωct+

(11)

频率项仅体现在式(11)中括号中的项,与一阶RC系统的频率响应是相同的。

3 内嵌碱金属磁力仪特性的数值仿真

直接对微分方程组式(1)进行数值求解,采用参数:ω0=2π×70kHz,ωc=ω0,β=1。

3.1 线性测量范围

(a)

(b)图2 磁力仪的线性测量范围 (a)数值仿真;(b)近似解Fig.2 The linear measurement range of magnetometer (a) Numerical simulation; (b) Approximate analysis

3.2 频率响应

场Bx的幅度定为100nT,改变它的角频率ω,得到磁化强度分量Mx随ω的归一化响应曲线如图3所示。

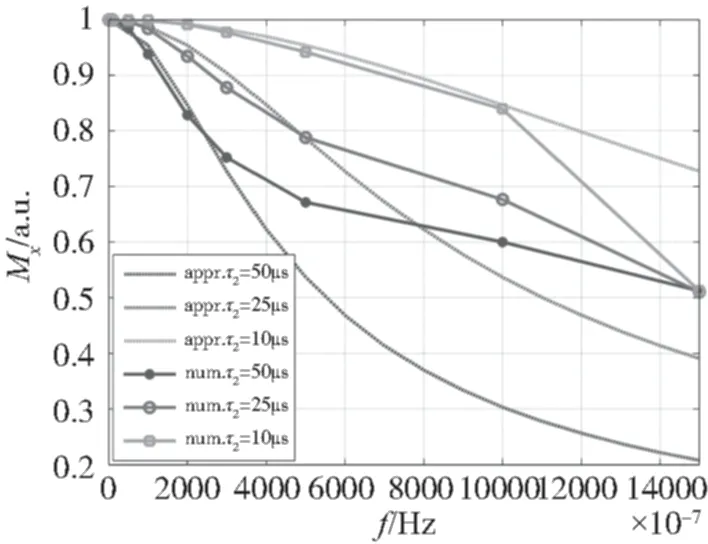
图3 内嵌碱金属磁力仪的频率响应(图中appr.为近似解,num.为数值解)Fig.3 Frequence response of embedded alkali magnetometer (The appr. and num. mean approximate and numerical solutions respectively)

从图3结果可知:1)磁力仪的频率响应近似于低通滤波器的频率响应曲线,它对低频信号响应较好，随着τ2增大,截止频率变小。2)对每一个τ2,频率较低时近似解与数值解基本重合,但当频率ω增大时,从式(10)到式(11)的近似条件不再满足,因此近似解误差增大。

4 结论

分别利用近似解析解和数值计算解研究了磁力仪的线性测量范围与频率响应。随着待测磁场增大,磁力仪响应偏离线性,且纵向与横向弛豫时间越长,线性测量范围越小。当待测磁场频率较低时,磁力仪的频率响应曲线与一阶低通滤波器相似,但当频率较高时,磁力仪的响应比较复杂,不能用一阶系统来近似。在核磁共振陀螺中,为了获得最佳的磁共振信号,需要结合磁力仪特性与自旋交换光极化参数进行优化。

[1] Lutwak R. Micro-technology for positioning, navigation, and timing towards PNT everywhere and always[C]. International Symposium on Inertial Sensors and Systems (ISISS). IEEE, 2014: 1-4.

[2] 丁衡高 . 海陆空天显神威：惯性技术纵横谈 [M]. 北京 : 清华大学出版社.

[3] Fang J C, Qin J. Advances in atomic gyroscopes: a view from inertial navigation applications[J]. Sensors, 2012, 12(5): 6331-6346.

[4] Kitching J, Knappe S, Donley E A. Atomic sensors-a review[J]. IEEE Sensors Journal, 2011, 11(9): 1749-1758.

[5] Gustavson T L, Landragin A, Kasevich M A. Rotation sensing with a dual atom-interferometer Sagnac gyroscope[J]. Classical & Quantum Gravity, 2000, 17(12): 2385-2398.

[6] 秦杰. 基于129Xe-Cs的SERF原子自旋陀螺仪原理实验研究[D]. 北京:北京航空航天大学, 2012.

[7] Kornack T W, Ghosh R K, Romalis M V. Nuclear spin gyroscope based on an atomic comagnetometer[J]. Physical Review Letters, 2005, 95(23): 230801.

[8] Eklund E J. Microgyroscope based on spin-polarized nuclei[D]. University of California at Irvine, 2008.

[9] Donley E A. Nuclear magnetic resonance gyroscopes[J]. Sensors IEEE, 2010, 143(2): 17-22.

[10] Larsen M, Bulatowicz M. Nuclear magnetic resonance gyroscope[C]. 2012 IEEE International Frequency Control Symposium, 2012: 1-5.

[11] 秦杰, 汪世林, 高溥泽, 等. 核磁共振陀螺技术研究进展[J]. 导航定位与授时, 2014, 1(2):64-69.

[12] Walker T, Larsen M. Spin-Exchange pumped NMR gyros[J].Advances in Atomic, Molecular, and Optical Physics, 2016, 65:373-401.

[13] Sargent M III, Scully M O, Lamb W E. 激光物理学[M]. 杨顺华, 彭放, 译.北京: 科学出版社, 1982.

[14] Cohen-Tannoudji C, Dupont-Roc J, Haroche S, et al. Diverses résonances de croisement de niveaux sur des atomes pompés optiquement en champ nul. I. Théorie[J]. Revue de Physique Appliquée, 1970, 5(1): 95-101.

Research on Alkali Metal Magnetometer for Nuclear Magnetic Resonance Gyroscope

LUO Hui, YANG Kai-yong, WANG Zhi-guo, Zhang Yi, XIA Tao, ZHAO Hong-chang

(College of Opto-Electronic Science and Engineering, National University of Defense Technology,Changsha 410073,China)

Nuclear magnetic resonance gyroscope measures angular rates with close loop magnetic resonance, where the magnetic resonance signal is read out with embedded alkali metal magnetometer. In order to improve the performance of the magnetometer, the Bloch Equations are solved with perturbation-iteration and series expansion method. Each component of the magnetic moment is obtained approximately. Then the linear measurement range as a function of longitudinal and transverse relaxation time is discussed. Moreover, the frequency response of the magnetometer is obtained. The approximate solution is verified with numerical simulation. It is found that the linear measurement range decreases when longitudinal and transverse relaxation time increases. The frequency response of the magnetometer is similar to one-order low pass filter and the cut-off frequency is related to transverse relaxation time. These findings is of significance to the optimization of nuclear magnetic resonance gyroscope.

Nuclear magnetic resonance gyroscope; Alkali metal magnetometer; Linear measurement range; Frequency response

10.19306/j.cnki.2095-8110.2017.01.015

2016-11-15；

2016-12-30。

国防科技大学科研计划项目(JC140702)

罗晖(1970-)，男，博士，教授，主要从事光电惯性技术方面的研究。E-mail: luohui.luo@163.com

V241.5

A

2095-8110(2017)01-0085-04