一种基于图像区域分块的SIFT快速配准方法

张红民，张见双，罗永涛，陈柏元



一种基于图像区域分块的SIFT快速配准方法

张红民，张见双，罗永涛，陈柏元

（重庆理工大学 电气与电子工程学院，重庆 400054）

针对传统尺度不变特征变换（SIFT）算法在特征提取与描述时计算量大、实时性差的问题，提出一种基于区域分块的SIFT的快速配准方法。首先，将匹配图像和待匹配图像分割成若干均匀的子图，通过计算每个子图的信息熵值与设定阈值比较来确定局部子图的特征类型；对筛选出来的特征区域的子图进行特征提取和生成PCA-SIFT描述子，对筛选出来的平坦区域直接跳过，不进行检测。实验结果表明：提出的方法在保证配准精度90%以上的情况下，计算时间减少了15%～25%左右，提高了图像配准的速度。

SIFT；区域分块；PCA-SIFT；图像配准

0 引言

尺度不变特征变换（Scale Invariable Feature Transform, SIFT）算法[1]因其在图像旋转、平移、尺度变换、光照变化、噪声干扰、仿射变换时鲁棒性强的优点，成为了近年来图像配准技术的研究热点[2-4]，但传统的SIFT算法复杂、耗时较长，难以满足工程实时性的要求[5]。针对这一问题，近年来许多国内外学者开展了相关研究工作。2014年，宋佳乾等人[6]提出Canny算子和K-L变换的改进SIFT算法，用来去除不稳定的边缘点，从而提高图像配准的速度。2015年，李玉峰等人[7]把Harris算子和SIFT结合起来实现了图像自动配准，提高了配准的速度和效率。2016年，张盼等人[8]利用变相加权环圆形邻域对SIFT特征向量进行描述，算法在速度上具有一定的优势。

虽然以上基于SIFT的改进算法在速度上有些改善，但计算量依然很大，实时性不强，本文提出了一种基于区域分块的SIFT快速配准算法，该算法先将配准图像和待配准图像分割成若干块均匀的子图；然后对分割的子图的信息熵值与设定的阈值比较来判断图像区域的类型；不同的子图区域类型采取不同的处理策略，加快了算法的速度。

1 传统的SIFT图像配准算法步骤

SIFT算法一般包括以下几个步骤[9-10]：

1）尺度空间极值检测

首先构造高斯金字塔，对DOG算子进行局部极值检测。通过对每个像素与其邻域比较来设定极值点并保存。

2）确定关键点的位置和尺度

通过拟合函数来精确定位特征点的位置和尺度，为了确保特征点的稳定性和抗噪性，要将对比度较低的点和边缘一些难定位的点剔除。

3）关键点的方向分配

对关键点为中心的邻域进行采样，并对邻域像素的梯度方向进行直方图统计，直方图中峰值的位置就是关键点邻域梯度的主方向，也就是关键点的主方向。

4）生成特征点描述子

将关键点为中心的16×16的矩形窗口均匀分成16个4×4个子窗口，然后计算每个子窗口8个方向的梯度累计值，这样每个特征点都会生成4×4×8＝128维的特征向量。

2 基于区域分块的SIFT快速配准算法

有SIFT算法的步骤可知，虽然传统的SIFT图像配准算法具有很多优良的特性，但该算法会提取过多的特征点和生成128维的特征描述子。使得计算量过大，实时性较差。针对这个问题，本文对传统的SIFT算法进行了改进，改进算法流程图如图1。

2.1 图像区域分块的思想

一般情况下，一幅自然图像中都会存在灰度变化明显和不明显的区域；只有在图像的灰度变化显著的区域，才会有较多的特征点，而那些灰度变化不明显的区域会很难提取出特征点，并且提取的特征点易产生误匹配。为了提高图像配准的效率，本文采用了减少图像特征检测范围的方法。首先将图像均匀分割成若干个子图，针对那些灰度变化不明显的子图，也就是子图含的信息量少的一些区域，就直接跳过，不进行特征检测，而对那些灰度变化明显，子图所含的信息量较多的一些子图才进行特征检测。

本文使用图像信息熵[11]来区分子图所含的信息量，信息熵值越大，代表该区域所包含的纹理信息越丰富，也就是特征点越多；反之，信息熵值越小，代表该区域所包含的纹理信息越稀少，特征点越少[12]。

2.2 图像区域分块算法的具体步骤

1）图像均匀分块，首先将图像分割成均匀的5×5个子图（若图像的像素数不能被5整除，则对少数边缘像素重复计算简化处理），子图编号为1, 2, …, 25；

图1 基于区域分块的SIFT快速配准算法流程图

2）计算每幅子图的信息熵值(1), …,(25)；

3）将每幅子图的信息熵值与规定的阈值进行比较，本文设置的阈值为经验值6.0；

4）特征区域判断，将子图图像信息熵值大于阈值的子图判断为特征区域；相反，小于阈值的子图判断为平坦区域；

5）对第4）步计算出的特征区域进行特征检测，平坦区域则直接跳过不进行特征检测；

6）对第5）步检测的特征点采用主成分分析法进行特征描述，生成PCA-SIFT描述子[13]。

7）最后对特征描述子采用最近邻与次近邻之比的方法对特征点进行配准。

3 实验验证与分析

为了验证本文改进算法的效果，进行了实验验证。硬件平台：CPU Intel（R）Core(TM) i5-2450M；内存为4GB；64位window7操作系统；软件平台：Matlab 2014a。本文采用图2所示的相机拍摄的具有一定重叠区域的3组实验图像，左为参考图像，右为待配准图像，图像大小分别为：(a)523×395，(b)560×542，(c)417×354。

图2 三组待配准图像

图3显示的是图2中的第2组图像(b)被分割成5×5均匀子图的模式情形，表1、表2分别列出了参考图像、待配准图像各个子图的信息熵值，每个数据代表图像中对应位置的信息熵值，从表中可以看出子图信息熵值较小的区域对应的是图像平坦区域，反之，信息熵值较大的子图区域对应的特征区域。本文中筛选子图的信息熵的阈值设置为经验值6.0，这样图3(a)中将有36%的区域直接跳过，不进行特征检测，图3(b)中将有28%的区域不进行特征检测，大大减少了特征提取时间。

为了验证本算法的实际效果，将其与传统的SIFT算法进行配准的效果比较，两种算法进行特征点数量、正确匹配点对数、运行时间、匹配正确率的数据统计比较，具体的数据见表3。

图3 图像分割模式

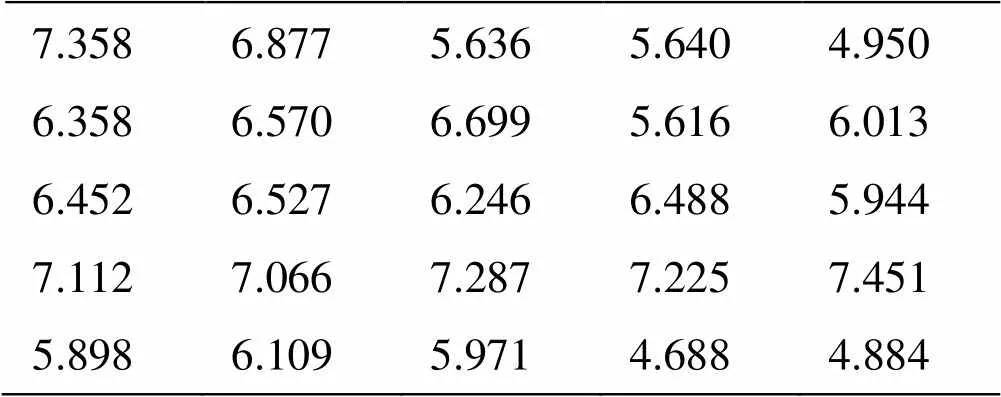
表1 图3(a)对应子图的信息熵值

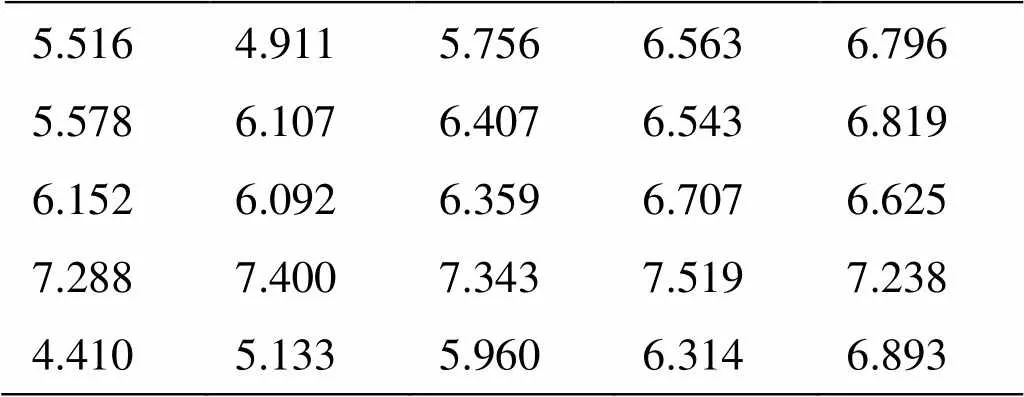
表2 图3(b)对应子图的信息熵值

如表3所示，本文算法虽然在特征点提取上有所减少，图像的配准点对数也有减少，但减少的数量有限，并不影响图像配准的准确性，在图像配准时间上却降低了整个图像配准的时间的15%～25%左右，如第3组图像测试数据，正确匹配点对数由173减少到167，但时间由2.254s减少到1.771s，减少了约21.4%。

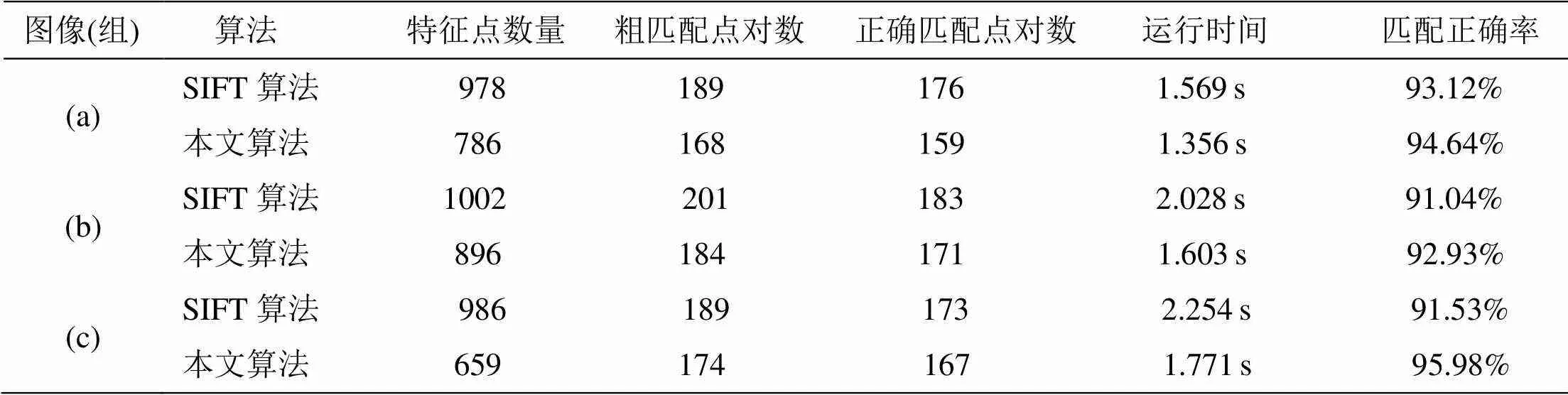
表3 两种算法结果对比

4 结论

本文通过图像纹理信息的分析的基础上，提出了一种改进的快速图像配准算法，首先将图像进行分块处理，分别求出每个子图的信息熵值，然后将每个子图的信息熵值与固定的阈值来比较，只对熵值大于阈值的特征区域进行SIFT特征提取和PCA-SIFT描述，最后使用最近邻与次近邻之比的算法对图像进行匹配。

为了验证本文算法的实际效果，将本文算法应用于实际的车载全视景图像拼接系统中，由于实际拍摄的图像大多具有部分平坦区域，本文算法在保证配准精度的前提下可明显降低了算法复杂度，计算时间则较传统的SIFT算法减少15%～25%左右。

值得一提的是，文中在对子图区域类型分类时，子图特征类型判断阈值设置的为经验值6.0，没有实现根据子图的信息自适应设定阈值，需要在今后的工作中进一步开展研究。

[1] LOWE D G. Distinctive image features from scale-invariant keypoints[J]., 2004, 60(2): 91-100.

[2] 王新华, 王晓坤. 十亿像素瞬态成像系统实时图像拼接[J].中国光学, 2015, 8(5):785-792.

WANG Xinhua, WANG Xiaokun. Real time image mosaic of the transient gigapixel imaging system[J]., 2015, 8(5): 785-792.

[3] 李玉峰, 李光泽, 谷绍湖, 等. 基于区域分块与尺度不变特征变换的图像拼接算法[J]. 光学 精密工程, 2016, 24(5): 1197-1205.

LI Yufeng, LI Guangze, GU Shaohu, et al. Image mosaic algorithm based on area blocking and SIFT[J]., 2016, 24(5): 1197-1205.

[4] 许佳佳. 结合Harris与SIFT算子的图像快速配准算法[J]. 中国光学, 2015, 8(4): 574-581.

XU Jiajia. Fast image registration method based on Harris and SIFT algorithm[J]., 2015, 8(4): 574-581.

[5] 邸男, 李桂菊, 魏雅娟. 采用SIFT的末制导图像匹配技术[J]. 红外与激光工程, 2011, 40(8): 1499- 1593.

DI Nan, LI Guiju, WEI Yajuan. Image matching technology based on SIFT for terminal-guiding system[J]., 2011, 40(8): 1499- 1593.

[6] 宋佳乾, 汪西原. 基于Canny算子和K-L变换的改进SIFT匹配算法[J]. 电视技术, 2014, 38 (15): 61-65.

SONG Jiaqian, WANG Xiyuan. Improved SIFT matching algorithm based on Canny operator and K-L transformation[J]., 2014, 38 (15): 61-65.

[7] 李玉峰, 王竹筠. 基于Harris-SIFT特征匹配的图像自动配准算法研究[J].电视技术, 2015, 39 (23): 26-30.

LI Yufeng, WANG Zujun. Automatic image registration algorithm research based on Harris-SIFT features matching[J]., 2015, 39 (23): 26-30.

[8] 张盼, 阮俊, 王雅继. 变环加权SIFT算法的图像拼接[J]. 现代电子技术, 2015, 38(19):72-78.

ZHANG Pan, RUAN Jun, WANG Yaji. Image mosaic based on SIFT algorithm of ring-conversion and weighting[J]., 2015, 38(19): 72-78.

[9] 张勇, 王志锋, 马文. 基于改进的SIFT特征点匹配的图像拼接算法研究[J]. 微电子学与计算机, 2016, 33(3): 60-64.

ZHANG Yong, WANG Zhifeng, MA Wen. Research image mosaic algorithm based on improved SIFT feature matching[J]., 2016, 33(3): 60-64.

[10] 韶阿俊, 钱惟贤, 顾国华, 等. 基于计算集成成像的图像配准算法研究[J]. 红外技术, 2015, 37(5): 398-403.

SHAO Ajun, QIAN Weixian, GU Guohua, et al. Image registration algorithm research based on computational integral imaging[J]., 2015, 37(5): 398-403.

[11] 吴泽鹏, 郭玲玲, 朱明超, 等. 结合图像信息熵和特征点的图像配准方法[J]. 红外与激光工程, 2013, 42(10): 2846-2852.

WU Zepeng, GUO Lingling, ZU Mingchao, et al. Improved image registration using feature points combined with image entropy[J]., 2013, 42(10): 2846-2852.

[12] 岳昕, 尚振宏, 强振平, 等. 基于信息熵与SIFT算法的天文图像配准[J]. 计算机科学, 2015, 42(6): 57-60.

YU Xin, SHANG Zhenhong, QIANG Zhenping, et al. Astronomical image registration combining information entropy and SIFT algorithm[J]., 2015, 42(6): 57-60.

[13] 李钦, 游雄, 李科, 等. PCA-SIFT特征匹配算法研究[J]. 测绘工程, 2016, 25(4): 19-24.

LI Qin, YOU Xiong, LI Ke, et al. Research on the matching algorithm of PCA-SIFT[J]., 2016, 25(4): 19-24.

A Fast SIFT Registration Method Based on Image Region Segmentation

ZHANG Hongmin，ZHANG Jianshuang，LUO Yongtao，CHEN Boyuan

(,,400054,)

For a large amount of computation and poor real-time performance of the traditional scale invariant feature transform(SIFT) algorithm in feature extraction and feature description, a fast registration method based on region segmentation SIFT is proposed. First, the matching image and the image to be matched are divided into several uniform subgraphs. The feature type of the local subgraph is determined by calculating the information entropy value of each subgraph and setting the threshold value. The features of the subgraph are extracted and the PCA-SIFT descriptor is generated. Then, the flat area screened out is skipped directly and not detected. Experimental results show that the proposed algorithm in ensuring the accuracy of registration of more than 90% of the cases, the calculation time is reduced by about 15%- 20%, and the speed of image registration is improved.

SIFT，regional block，PCA-SIFT，image registration

TP391.41

A

1001-8891(2017)04-0341-04

2016-09-30；

2016-12-30.

张红民（1970-），男，河南舞阳人，博士，教授，主要研究方向为图像处理与模式识别。E-mail：hmzhang@cqut.edu.cn。

重庆市基础与前沿研究计划项目（cstc2015jcyjA40051）。