径流曲线数(SCS-CN)模型在洪水预报中的应用研究
王 冬,李 丽,王加虎,余娇娇,梁菊平,赵永超
(河海大学水文水资源学院,南京 210098)
水文模型、土壤侵蚀模型以及非点源污染模型常作为研究水资源危机、土壤侵蚀、非点源污染等热点问题的技术工具[1]。目前,流域工程规划和设计中都广泛应用水文模型,特别是能够反映流域的土壤透水性、降雨强度、土壤水分等下垫面因子的分布式水文模型。常见的分布式水文模型有TOPMODEL、SWAT以及SWMM等,其中径流计算作为计算的基础是其重要的组成部分,现行的径流计算方法有很多,有Green-Ampt入渗曲线、Horton入渗曲线和Philip入渗曲线等[1],但利用上述方法进行径流计算过程中有不易获取的资料,且参数多,这限制了它们的广泛应用。
SCS-CN模型由美国农业部土壤保持局(USDA SCS)[2-4]提出,由于对输入数据量要求不高、模拟精度高而被许多国家和地区广泛应用[5,6]。该模型结构简单,其中径流曲线数(CN)是其需要的唯一综合参数,它是用来反映降雨前流域下垫面特征的无量纲参数,与土壤类型、前期土壤湿度、土地利用以及坡度等因素有关[7]。我国对SCS-CN模型应用研究较晚,大多研究者是移用或修正该模型,并应用到不同的研究区域,如:王红艳等人用降雨量、降雨强度和初损率对模型进行优化修正,并在黄土高原进行应用[7];王瑾杰等人以参数率定的新视角对模型进行总结和应用[8];符素华等人通过不同的方法计算北京地区的CN值并对其进行比较[9];王白陆对SCS模型进行改进,提高模型计算精度并在小流域范围应用[10]。
本研究对湖北省松柏站的降雨径流资料,利用降雨径流-反推和参数自动优选法两种方法,通过考虑不同前期湿度条件下的流域综合CN值的改变,来探讨SCS-CN模型在洪水预报中的应用及其精度问题,这对于提高径流预报能力有重要的意义。
1 研究方法
1.1 产流计算
本文选用SCS-CN模型计算产流,该模型是基于水量平衡和两个基本假定[2]存在的。用公式可分别表示如下:
水平衡方程:
P=Ia+F+Q
(1)
假设一,比例方程:
(2)
假设二:初损(Ia)与潜在蓄水能力(S)的关系:
Ia=λS
(3)
式中:P为降雨量,mm;F为实际入渗量,mm;Q为径流深,mm;Ia为初损;S为潜在蓄水能力,mm;λ为初损率。
由方程(1)、(2)、(3)可以建立SCS-CN模型地表径流计算方程为:
(4)
通常公式(3)中的初损率λ=0.2,因此由(3)和(4)有:
(5)
Q=0P≤0.2S
上述式中S与CN值的经验转换关系如下:
(6)
式中:CN值是径流曲线数,是流域特性的综合反映,与土壤、土地利用等有关。
由公式(5)和(6)分别反推出以下公式:
(8)
根据式(7)和(8)可计算出某次降雨径流一定前期湿度条件下CN值。
1.2 汇流计算
本文采用的是三水源汇流结构。以地表水为例:在水文模型中,按照常用的各水源汇流符合线性叠加原理的假定,不同栅格的自由水在流域上会以不同的流速、沿着各自的路径先后到达出口断面(其中自由水指的是产流和分水源计算的结果),按照指定的时段累加所有先后到达出口断面的各个栅格水量,形成地表水汇流时段单位线,利用该单位线对产流和分水源模块计算出的水量过程进行卷积计算,就得到了地表水源的汇流计算结果。
1.3 前期湿度条件的确定
美国土壤保持局[4]考虑前期土壤湿度对径流的影响,引入了前期降水指数API(Antecedent Precipitation Index),API在数量上即为降雨前5d的降雨总量(mm)。前期土壤湿度条件(Antecedent Moisture Condition,简称AMC)根据前期降水指数API可以划分为3级:干旱(AMC1),正常(AMC2)和湿润(AMC3)。具体划分依据见表1。

表1 前期土壤湿润条件分类Tab.1 The classification of antecedent moisture conditions(AMC)
2 研究区概况与数据来源
松柏站位于南河流域下的青杨河上,其控制面积为108.79 km2,区域土壤质地为单一的壤土,内有松柏水文站和九龙池、栏马、泮水和松柏四个雨量站。南河流域是汉江支流,位于神农架林区(109°56′~110°58′E,31°35′~31°57′N)的中部和东北部,包括神农架林区的松柏镇、宋洛乡、阳日镇等,河道总长度819.618 km,流域面积1 385.62 km2,河网密度为0.000 59 km-1,是林区中流域流量最大、面积最广的河流,内有青杨河等大小溪流112条。流域地处中纬度北亚热带季风区,气温偏凉多雨,降水量充沛。神农架林区多年平均径流总量为22.004 亿m3,多年平均径流量为726.5 mm,年径流系数为0.65[11]。
由于研究区域降雨径流资料年限不同,为避免出现较大的抽样误差,故尽可能选择产流资料年限较长且具有代表性的资料源[12]。本文选用资料条件较好的湖北省松柏站及其控制区域内四个雨量站1983-2012年的降雨径流资料,该资料来源于水文局,具有一定的代表性。研究区域的地形水系图如图1所示。
3 模型应用
基于研究区域的实测降雨径流数据,分别用降雨-径流反推法和参数自动优选法计算流域综合CN值,将1983-2003年的数据用于模型参数的率定,2004-2012年的数据用于检验模型的模拟效果以及参数的适用性。共计挑选出率定期次洪20场,验证期次洪10场。
3.1 模型率定
3.1.1 降雨-径流反推法
降雨-径流反推法是根据降雨和径流的匹配资料,对选出的次洪利用公式(7)和公式(8)计算出相应的潜在蓄水能力S值与流域综合CN值。利用该方法对率定期(1983-2003年)挑选出的次洪进行模拟,模拟结果见图2和表2所示。
3.1.2 参数自动优选法
参数自动优选法是根据数学理论确定参数优选法则,汇编计算机语言,建立自动搜索过程,直至确定流域综合最优CN值的算法。本文采用的参数优选算法为迭代ARS方法——在一定数量的随机搜索算法的基础上、根据优选指标交替减小参数变域,最终获得各个参数的优值区间。其原理可具体描述为每个参数都有一个可以用最小值到最大值的区间来表示的参数范围,在某一次的随机搜索时,每个参数都先按照平均分布在其取值范围内随机生成一个参数值,然后模型在随机生成的参数组控制下计算出模拟值,最后将模拟值与基准值比较得到相应的优选指标,完成一次随机搜索计算。本文采用的ARS迭代方法主要对快速径流出流系数、快速径流滞时、中速/快速出流比值、中速/快速滞时比值及单位面积基流等参数进行优选。根据此法对率定期(1983-2003年)挑选出的次洪进行模拟,模拟结果见图3和表3。

图1 研究区区域概况图Fig 1 Regional survey chart of the study area
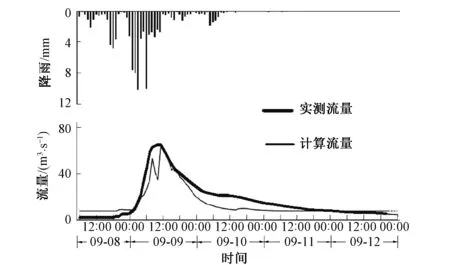
图2 流域率定期(1983-2003年)次洪830909模拟结果图Fig 2 The 830909 simulation diagram of basin during calibration period(1983-2003)
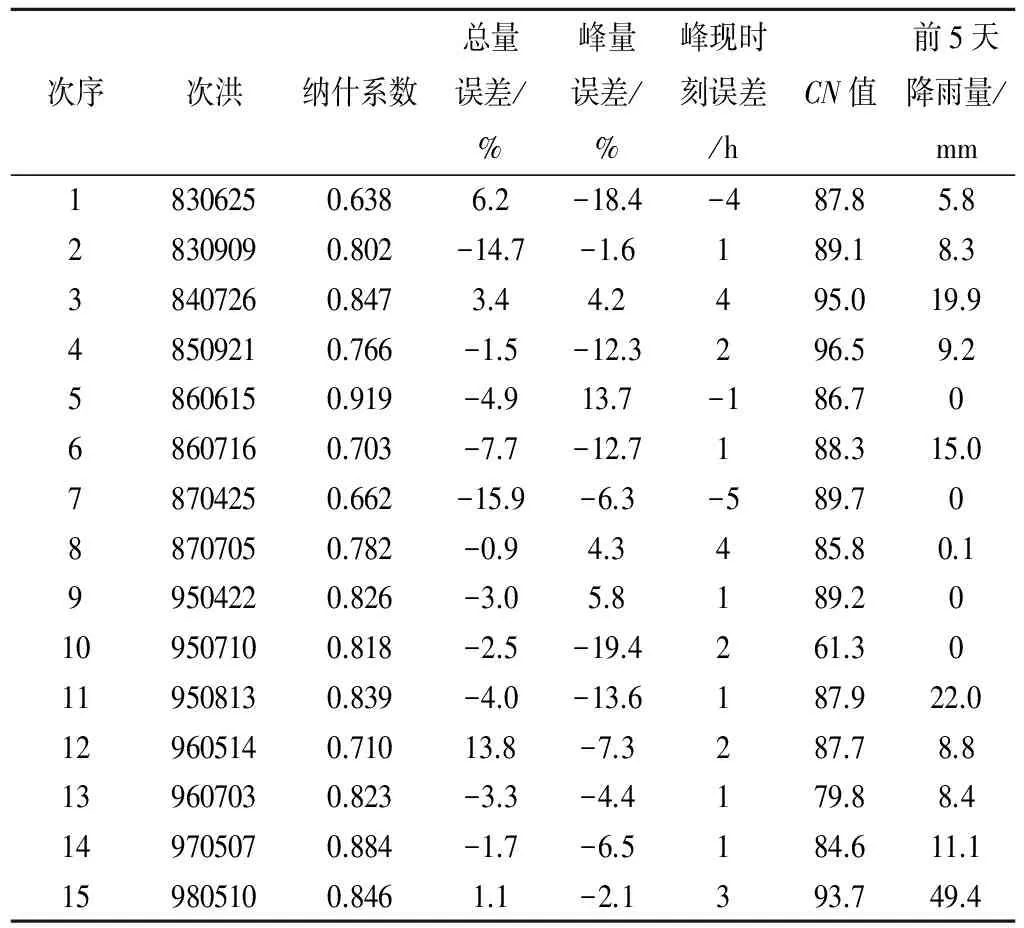
次序次洪纳什系数总量误差/%峰量误差/%峰现时刻误差/hCN值前5天降雨量/mm18306250.6386.2-18.4-487.85.828309090.802-14.7-1.6189.18.338407260.8473.44.2495.019.948509210.766-1.5-12.3296.59.258606150.919-4.913.7-186.7068607160.703-7.7-12.7188.315.078704250.662-15.9-6.3-589.7088707050.782-0.94.3485.80.199504220.826-3.05.8189.20109507100.818-2.5-19.4261.30119508130.839-4.0-13.6187.922.0129605140.71013.8-7.3287.78.8139607030.823-3.3-4.4179.88.4149705070.884-1.7-6.5184.611.1159805100.8461.1-2.1393.749.4

续表2 流域降雨-径流反推法率定期(1983-2003年)次洪模拟结果

图3 流域率定期(1983-2003年)次洪830909模拟结果图Fig.3 The 830909 simulation diagram of basin during calibration period(1983-2003)

次序次洪纳什系数总量误差/%峰量误差/%峰现时刻误差/hCN值前5天降雨量/mm18306250.7670.1-12.7393.05.828309090.910-3.19.2092.08.338407260.8602.8-19.9395.519.948509210.8062.5-3.9297.09.258606150.9585.015.0-190.0068607160.8494.4-7.0092.015.078704250.799-3.83.2193.0088707050.848-1.414.3490.00.199504220.8834.01.2294.20109507100.8410.2-10.6366.00119508130.9213.25.7090.022.0129605140.890-8.3-9.3393.08.8139607030.865-0.5-9.8183.08.4149705070.92019.84.5190.011.1159805100.8786.95.9395.049.4169904150.7909.2-3.2390.04.0170006240.836-0.410.0193.023.3180107240.9700.27.7095.946.2190205200.8571.14.4796.013.1200307040.9760.30.7095.043.5
从上面两表可以看出,通过两种方法计算的SCS模型模拟松柏站的降雨-径流关系效果较好,参数率定期纳什系数大于0.6,最高可达0.976。
3.2 模型验证
由于前期湿度条件对CN值有很大的影响,故对于上述两种方法计算出的流域综合CN值首先根据前期湿度条件(AMC)对次洪进行等级划分,对不同等级前期湿度条件下的CN值进行算术平均运算,结果如表4所示;继而把验证期的次洪根据AMC进行等级划分,取与率定期相应的AMC等级所对平均流域综合CN值,将CN值应用于验证期。当纳什系数在0.6以上,总量误差和峰量误差在±20%之间,峰现时刻误差在±3 h内视为合格。结果见图4和表5、表6:其中图4为次洪040603验证模拟结果图,第一场为降雨-径流反推法验证模拟结果图,第二场为参数自动优选法验证模拟结果图。
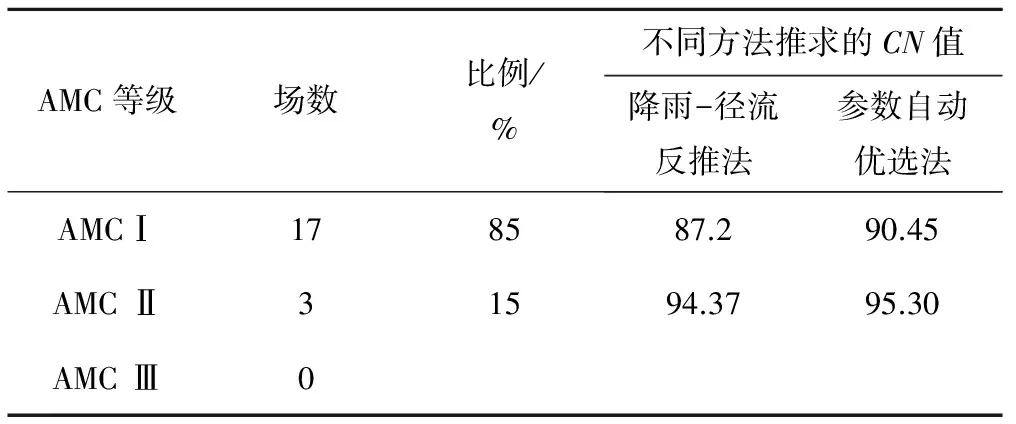
表4 率定期不同AMC等级下的CN值Tab.4 The CN value at different AMC grade during calibration period
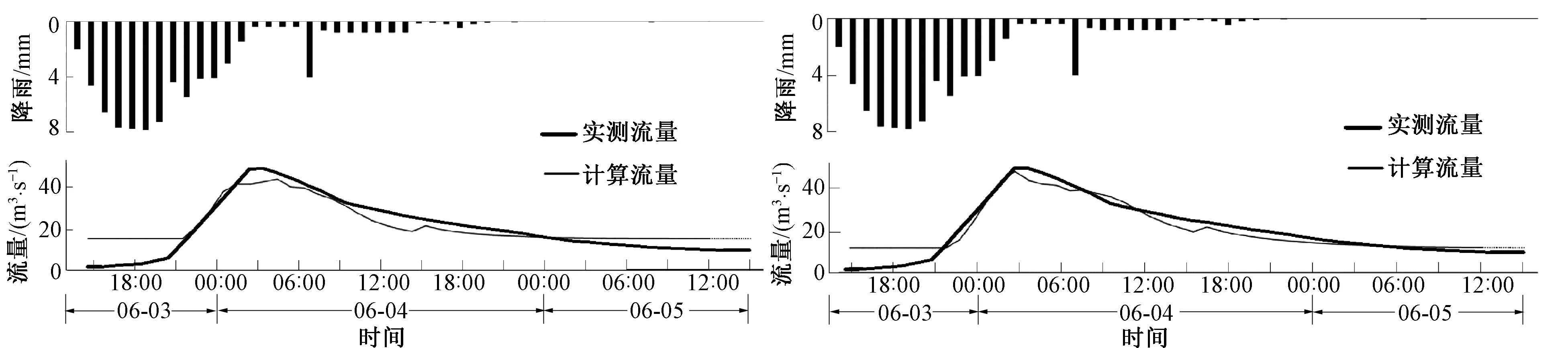
图4 流域验证期(2004-2012年)次洪040603验证模拟结果图Fig 4 The 040603 simulation diagrams of basin during validation period(2004-2012)
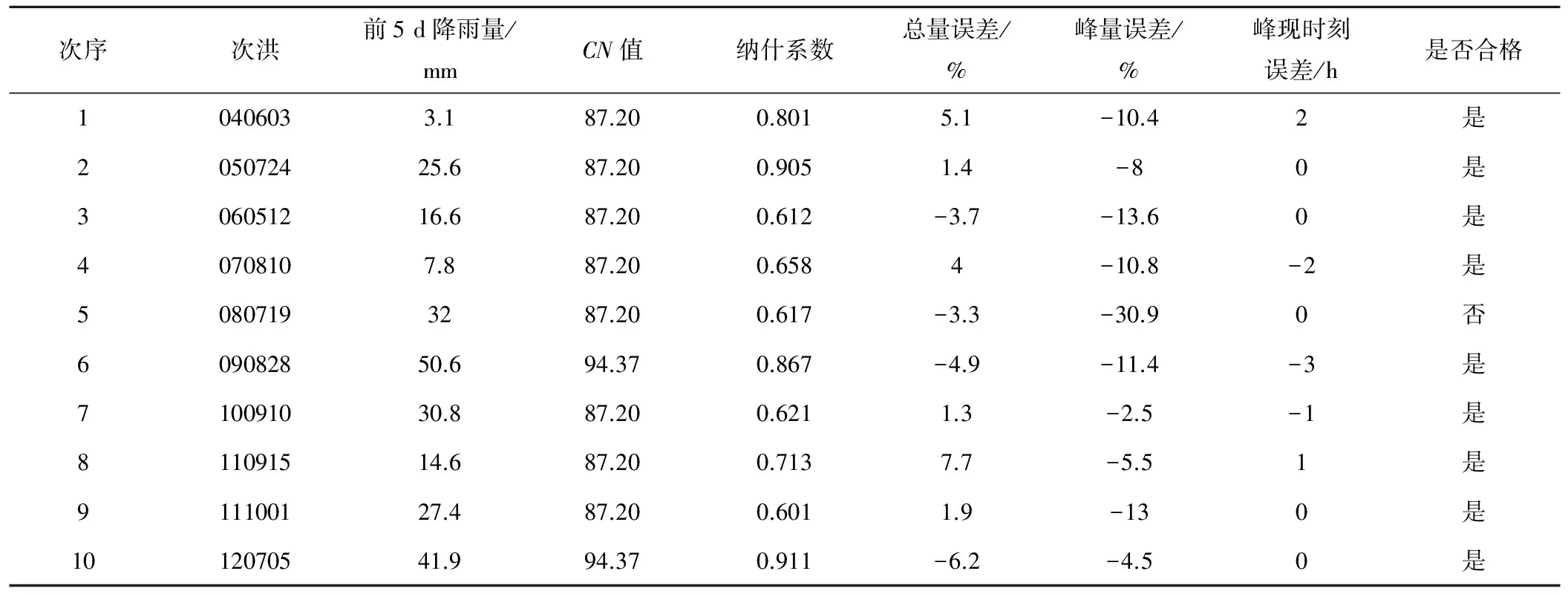
次序次洪前5d降雨量/mmCN值纳什系数总量误差/%峰量误差/%峰现时刻误差/h是否合格10406033.187.200.8015.1-10.42是205072425.687.200.9051.4-80是306051216.687.200.612-3.7-13.60是40708107.887.200.6584-10.8-2是50807193287.200.617-3.3-30.90否609082850.694.370.867-4.9-11.4-3是710091030.887.200.6211.3-2.5-1是811091514.687.200.7137.7-5.51是911100127.487.200.6011.9-130是1012070541.994.370.911-6.2-4.50是
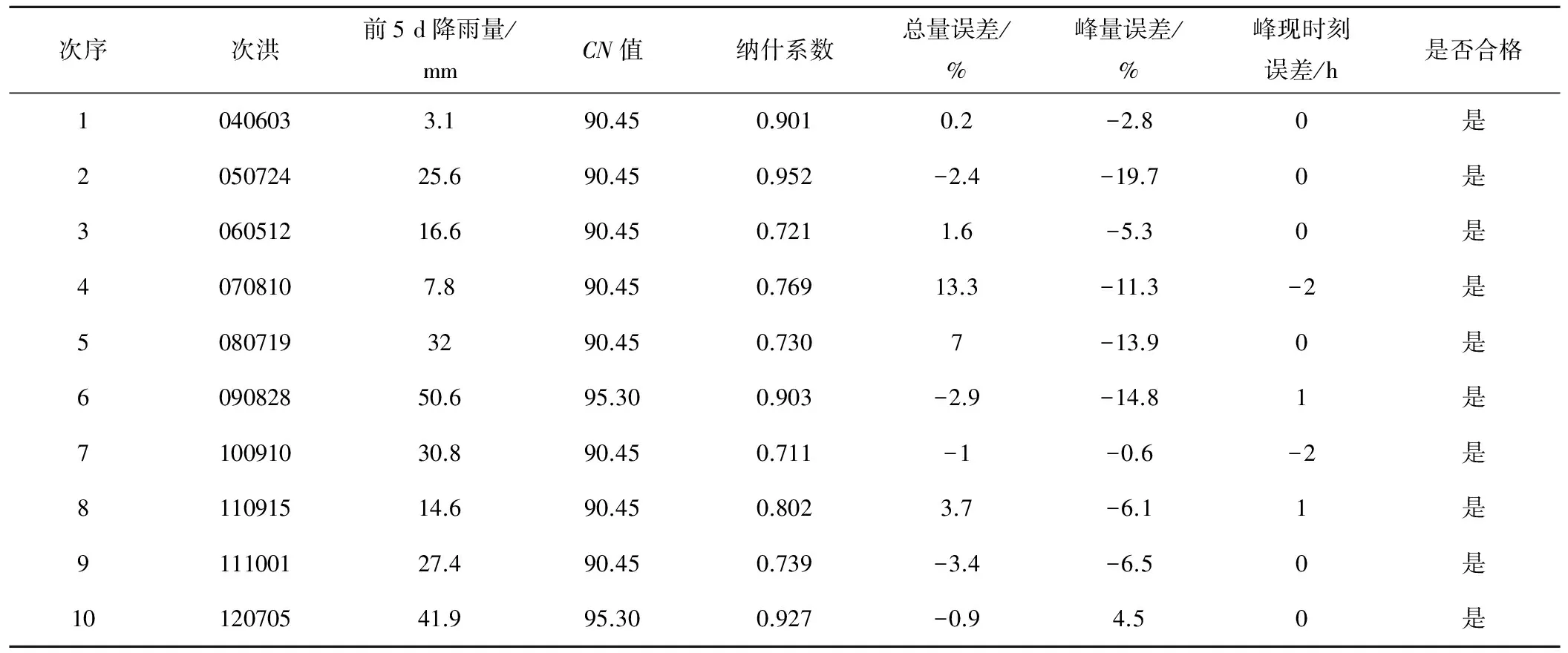
表6 流域参数自动优选法验证期(2004-2012年)次洪模拟结果Tab.6 Simulation results of basin during validation period (2004-2012)by automatic optimization method of parameters
由验证期的结果可以看出,采用通过前期土壤湿度条件改变CN值的方法用于验证期模拟径流的效果很好,合格率为90%以上,因此将考虑前期湿度条件计算出的流域综合CN值用于湖北省松柏站洪水预报的研究方案是可行的。
3.3 结果对比
(1).两种方法对比:两种方法率定期及验证期的参数CN均值及纳什系数均值见表7所示,可以看出,参数自动优选法无论率定期还是验证期均比相应降雨-径流反推法预报精度更高,且考虑了前期湿度条件影响下的模拟效果更好。
(2).模拟结果与实测值对比:由模型应用结果中可以看出,总量误差按照20%许可误差衡量,合格率为100%;峰量误差按照20%许可误差衡量,合格率为98.3%;峰现时刻误差绝对值(因为峰现时刻误差有正有负)的平均值为1.6 h;纳什系数的平均值为0.816,这表明径流模拟结果与实测值之间的吻合程度较好。
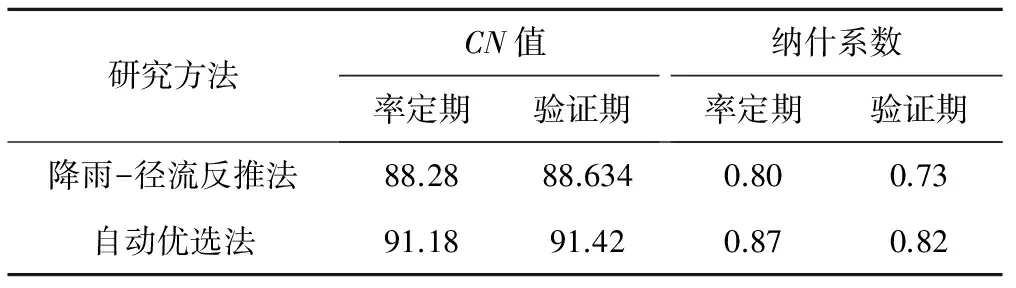
表7 两种方法径流模拟参数及结果Tab.7 Runoff simulation parameters and results of two types
4 结 语
(1).对湖北省松柏站1983-2012年的洪水过程进行模拟和验证的结果表明:使用降雨-径流反推法和参数自动优选法计算出的流域综合CN值,都可用于本流域的洪水预报,且考虑前期土壤湿度条件影响下的CN值变化效果更好。
(2).通过对两种方法得到的纳什系数的比较可以发现,参数自动优选法得到的CN值精度更高,模拟效果更好,因此建议在进行洪水预报时采用参数自动优选法。
(3).本文研究了不同的方法在有资料流域洪水预报中的应用,日后可涉及对空间外推能力的研究来确定无资料流域的流域综合CN值,以进行洪水预报。
□
[1] 符素华,王向亮,王红叶,等.SCS-CN径流模型中CN值确定方法研究[J].干旱区地理,2012,35(3):415-421.
[2] Soil Conservation Service (SCS). “Section 4, hydrology”. national engineering handbook[R].U.S. Department of Agriculture,Washington,D.C.1972:10.5.
[3] Soil Conservation Service (SCS). Hydrology in National Engineering Handbook, Supplement A, Section 4, Chap.10, Soil Conservation Service[R]. USDA, Washington, 1985:10.5.
[4] BOUGHTON W C A. Review of the USDA SCS curve number method [J]. Australian Journal Research. 1989,27(3):511-523.
[5] JUNG J W, YOON K S, CHOI D H, et al. Water management practices and SCS curve numbers of paddy fields equipped with surface drainage pipes [J]. Agricultural Water Management, 2012,110:78-83.
[6] REISTETTER J A, RUSSELL M. High-resolution land cover datasets, composite curve numbers, and storm water retention in the Tampa Bay, FL region [J]. Applied Geography, 2011,31(2):740-747.
[7] 王红艳,张志强,查同刚,等.径流曲线数(SCS-CN)模型估算黄土高原小流域场降雨径流的改进[J].北京林业大学学报,2016,38(8):71-79.
[8] 王瑾杰,丁建丽,张 成.普适降雨-径流模型SCS-CN的研究进展[J].中国农村水利水电,2015,(11):43-47,53.
[9] 符素华,王红叶,王向亮,等.北京地区径流曲线数模型中的径流曲线数[J].地理研究,2013,32(5):797-807.
[10] 王白陆.SCS产流模型的改进[J].人民黄河,2005,27(5):24-26.
[11] 李学国,汪正祥,朱俊林,等.神农架林区河流水文特征初步研究[J].湖北大学学报(自然科学版),2013,35(1):6-10.
[12] 石 月.汤旺河流域水文资料的“三性”分析[J].黑龙江水利科技,2015,43(1):16-19.

