基于改进Tennant法的河流生态基流量计算

杨裕恒，曹升乐，刘 阳

(山东大学土建与水利学院，济南 250061)

0 引 言

河流生态基流量定义为“维持河流中动植物等生物群落稳定，河流生态环境与功能不受破坏所需要的基本水量[1,2]”，其计算值应是一个长期观测、较为稳定的值。根据Tharme[3]对生态基流量计算方法的总结，其计算方法大致可分为四类：水文学方法、水力学方法、生态流量分析法和生态环境模拟法。目前，水力学方法、生态流量分析法和生态环境模拟法在我国实际运用中易遇到生态监测资料不足、人力物力有限等问题[4]，所以国内使用较多的方法是水文学法。该方法核心是应用相关的水文指标，通过长系列流量资料来推求相应的河流生态需水量、生态基流量等指标。在水文学方法中，Tennant法是应用较广泛的方法，它是田纳特等专家研究了11条受人类活动影响很小的河流，观测了河流在不同的流量与过流面积等条件下，对渔业的影响并汇总命名成Tennant法。Tennant法优点在于只需获得当地一段较长时间的流量资料，就能根据相应系数快捷计算出当地河流生态基流量，且计算结果较为合理[5]。但它侧重考虑流量年际变化，淡化了河流丰水期与枯水期流量的差距[6]，对于不同功能定位河流没有分类讨论。我国北方地区河流呈现出明显的季节性变化，汛期与非汛期流量差异显著，河流生态基流也随季节显著变化[7]。受人类活动的影响，我国北方地区大部分天然河流、城市河流径流量逐年减少[8]，定义这种河流为未补水河流；但也有小部分河流由于调水、人工补水、河流改道等原因流量逐年增大，定义这种河流为补水河流。鉴于此，本文针对不同河流功能定位与径流量的变化趋势，提出了一种对径流过程还原或还现的方法修正年均流量，并考虑河流年内径流变化以及生态过程对水文过程的影响，对Tennant法进行改进。

1 研究方法

1.1 Mann-Kendall法

Mann-Kendall法简称M-K法，是一种适用于非正态分布[9]的无分布检验方法。该方法的优点在于可以排除数据中极端值的干扰，也无需样本具有一定的统计分布规律，并且计算简便[10]，在水文学上广泛应用于研究降雨、径流等方面序列变异诊断[11]。

对于某一个样本容量为n的时间序列X(X1,X2,…,Xn)，构造它的秩序列：

(5)

式中：Dτ为第i时刻时所有大于j时刻数值的个数累计值；τ为i的取值范围，τ=1,2,…,n；n为样本容量；Ri为i时刻时依据Xi与Xj的大小取值0或1；Xi为i时刻的数值；Xj为j时刻的数值，j=1,2,…,i；UFτ为Dτ标准化计算后得到的值；E(Dτ)、V(Dτ)为Dτ的均值和方差。

通过查找正态分布函数表，可以得出在一个显著水平为α时的临界值Uα，若公式(3)所计算的|UFτ|>Uα，则该序列存在明显的上升或者下降的变化趋势。同理，以逆序列{Xn,Xn-1,…,1}重复以上过程，令UBτ=-UFτ，其中τ=n,n-1,…,1，根据UFτ和UBτ值绘制UF和UB曲线图，若UFτ和UBτ值小于0，则序列呈现下降趋势，反之则为上升趋势。若UFτ和UBτ曲线相交在临界值Uα=±1.96之间(α=0.05)，则交点对应的时刻有可能为序列变异开始时刻。

1.2 径流还原与还现计算

1.2.1 未补水河流的还原计算

一般情况下受人类活动影响的未补水河流，河流径流量呈现逐年减少的趋势。部分北方河流甚至出现断流，严重危害了河流健康。在此大背景下，导致径流突变点前后的径流量不能视为同一个整体。因此，为了保障北方地区未补水河流的水文情势不受破坏，避免极端径流序列资料对计算结果造成影响，计算生态基流量时有必要对径流序列进行还原[12]。

本文采用降雨-径流关系法进行径流量的还原计算。通过1.1节的方法找出河流径流突变点，找出受人类活动影响较小的降雨-径流资料，建立降雨径流关系。通过建立的降雨-径流关系和估算年份的降雨资料，计算出受人类影响较小的下垫面条件下的还原年径流量，以此完成还原计算。

1.2.2 补水河流的还现计算

我国近年来对河流的开发利用程度提高，尤其是部分城市河流为满足景观、生活需求大量补水，径流量往往较未补水前有明显的增大，其水文过程已与未补水河流有较大差别。经过补水的河流利用还原径流序列进行生态基流量计算必然会使计算结果偏小，造成误差[13]。因此，在计算此类河流生态基流量之前，需筛选出突变点之后受到人为影响较大的径流资料，进行径流量还现计算，增加径流系列资料的可靠性与一致性，使其更符合实际情况。将河流还现计算归纳为，为满足流域经济、生态要求所补水的河流，其核心在于维持河流当前的水文情势过程，因此在计算时应把早期下垫面状况下产生的径流量修正为现状(或近期)条件下的径流量。

对于径流还现方法与1.2.1节还原计算相似，不再赘述。

1.3 水文过程与生态过程的耦合的Tennant法

1.3.1 典型年以及分期百分数的选取改进

本文选用典型年的年内流量过程来代替河流多年平均流量，典型年流量过程更能体现流量的年内丰枯变化规律，即使用典型年的Tennant法求出的生态基流量更为合理[14]。对于补水河流，从突变点后选取典型年，对于未补水河流则相反。根据北方河流周期变化及生态需水的特点，10月至次年3月降水较少，河道水量较枯，水生动植物进入冬眠期，生态需水量相对较小[15]，将其定义为一般用水期；4月至9月用水量增加，鱼类逐渐进入产卵期、幼鱼生长发育期，生态需水量相对较大[5]，将其定义为鱼类产育期。在一般用水期河流径流量较小，Tennant法认为多年平均流量的10%为河道流量的最低下限[16]，故选用多年平均流量的10%作为生态基流的计算基准。而在鱼类产育期，河流需水量加大，10%的河道流量难以满足生活、生态用水的最低要求。参考相关文献的设定标准[17,18]，选取4月至9月修正后流量的15%作为河流生态基流量能较好地满足河流与生物的最低要求。具体生态基流量分期百分比的选取如表1所示。

1.3.2 月均流量改进

鱼类产育期按照生态基流量的定义，在满足河流不受破坏的同时，还应满足鱼类等水生生物能够正常产卵、繁育等需求。

表1 生态基流量分期百分比的选取 m3/s

对于不同河流，首先需要明确重要保护鱼类繁殖习性和生境条件，4月上中旬鱼类开始产卵，需水量增大；4月下旬-5月大部分鱼类产卵，需水量持续增大。当河流水位下降或者河流流速达不到要求时，鱼类会停止产卵行为[19]；6-9月水温较高，鱼类索饵旺盛，为生长期，需要洪水将大量的树叶草枝叶等有机物带入河道。若河流没有特定保护鱼类，则可以参照四大家鱼的习性。4月开始，鱼类逐渐开始为产卵进行准备，根据相关研究，河流流速0.20～0.25 m/s是鱼类产卵所需的最低流速[20,21]，鱼卵安全漂浮下限为0.25 m/s[19]。8月为鱼类产育高峰期，从4月涨水期开始至8月流速最大期，河流流速至少增加0.1 m/s。因此，针对特定保护鱼类产育习性，应将鱼类生长繁育规律与水文情势变化的耦合在原Tennant法的基础上增加一个流速条件，满足鱼类生存繁衍要求，计算流程如图1所示。

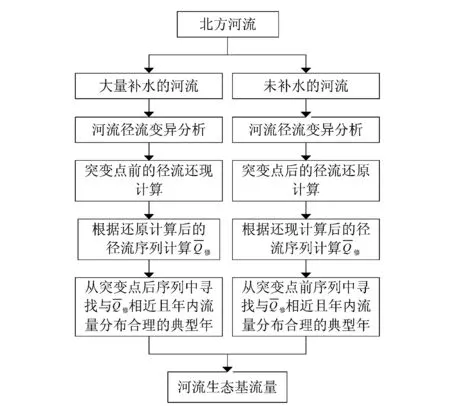
图1 河流生态基流量计算流程图Fig.1 Flow chart of river ecological basic flow

2 实例应用

2.1 天然河流的生态基流量计算

2.1.1 河流介绍

沂河是山东境内发源的第一大河。随着沂河流域城市化速度的加快，流域经济发展对沂河水资源的依赖程度不断提高，综合用水量也不断上升[22]。沂河流域内由于地形与降雨等原因，径流年内波动剧烈，汛期径流量较大，易造成难以利用的洪水资源；而枯水期径流量偏小，部分河段甚至出现了断流，影响了河流健康与流域经济的发展。因此，通过沂河径流年际变化规律、年内分配特征，有针对性的计算沂河生态基流量，对沂河流域水资源的合理开发与保护有着重要意义。

2.1.2 径流变异诊断分析与还原计算

对沂河流域逐年流量序列通过M-K法进行变异诊断分析，计算结果如图2所示。图2显示，曲线的交点在1967年，经过查证，60年代沂河修建大量水库开始对河流流量造成扰动[21]，故选取1967年为该阶段变异点。从图2，可以看出变异点之后流量呈现逐年减小的趋势明显，因此主要研究变异点之后的流量序列，对其进行还原计算。

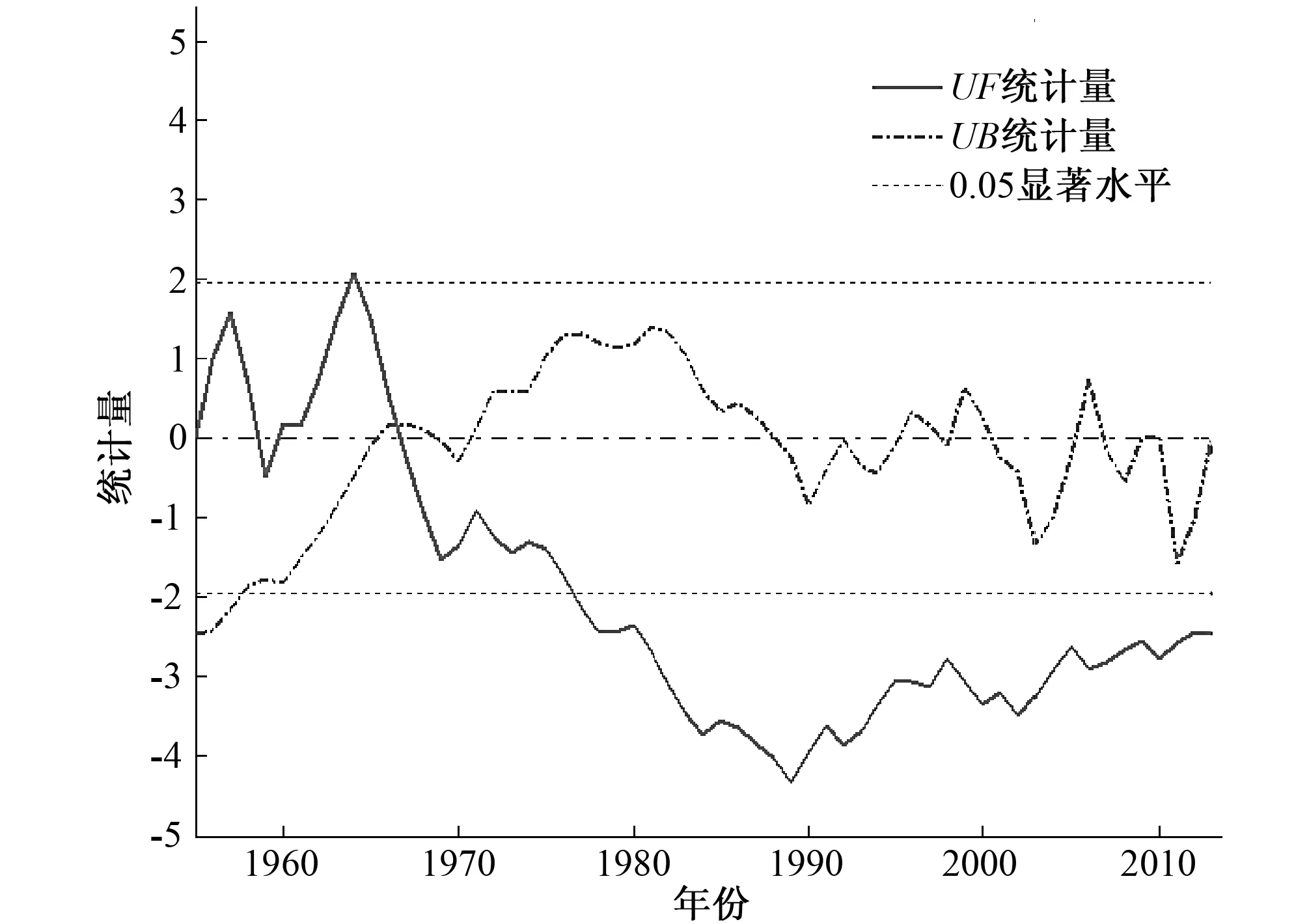
图2 沂河流域流深序列的Mann-Kendall法变异诊断结果Fig.2 Mann-Kendall variation diagnosis results of runoff series of Yihe River

同一流域内，在降水量相同的条件下，下垫面不同，径流产流量也不同。以图3中1955-1966年降水-径流散点为依据，建立降水-径流关系式，得到1955-1966年的降水-径流关系式为y=0.150x-76.11，序列相关系数R2=0.889，表明变异点前沂河受人为活动影响较小，降雨径流相关性良好。应用此关系式对突变点后的径流进行模拟，结果如图4所示。图4显示，突变点之后由于气候变化、下垫面变化和其他人类活动等原因，实测流量明显减小。因此，流量还原之后的生态基流分析，对恢复河流的天然水文情势具有一定意义。

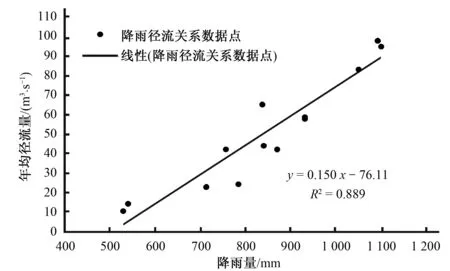
图3 沂河流域降水径流线性相关分析Fig.3 Linear correlation analysis of rainfall and runoff in YiheRiver Basin

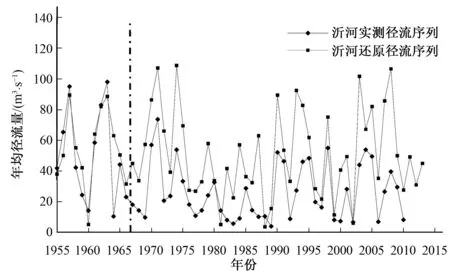
图4 沂河实测及还原流量序列图Fig.4 The measured flow and flow reduction sequence diagramin Yihe River

2.1.3 典型年的Tennant法计算生态基流量

根据还原后的流量序列，计算得1955-2013年沂河平均流量为51.76 m3/s，比修正之前的流量提高了39.9%。通过选取

突变点前典型年的方法，选取1961年实测逐月流量序列通过同倍比缩放至修正后的多年平均流量，再乘以不同时期所对应的流量百分数，计算得经过还原分析的沂河逐月生态基流量，见表2、图5所示。从表2、图5中可以看出原Tennant法未能满足鱼类产育要求，而选取典型年逐月流量考虑的鱼类产育最低流速，更易满足生态功能最小需水量的要求。综合分析，利用流量还原修正年均流量并使用典型年改进的Tennant方法能够更好地反映沂河天然水文情势，有助于保障河流流速、水深度、河流生物量，保障河流环境良性存在和发展，结果较为合理。

2.2 补水河流的生态基流量计算

2.2.1 河流介绍

小清河位于山东省中部地区，流经省内经济最发达的区域之一，是济南市重要的一条独流入海河流。小清河历史上曾是一条具有防洪、排涝、灌溉、航运、景观等多功能的人工运河。近年来，为满足小清河污染治理及航运的需求，政府通过卧虎山水库、提取黄河水的方式补充小清河水量[23]，小清河黄台桥断面结构图及补水前后年均水位关系如图6所示。目前，小清河流量较补水之前有较大提升，并初步满足通航要求及污染治理要求。对于小清河流域生态基流量的研究，需主要分析小清河补水之后年际变化规律、年内分配特征。有针对性的计算小清河生态基流量，对小清河流域污染治理、流域经济社会发展有着重要意义。

表2 修正前后的沂河逐月生态基流量计算表 m3/s

图5 修正前后的沂河逐月生态基流量曲线图Tab.5 The monthly ecological base flow curves before and after correction in Yihe River

图6 小清河河流结构及水位图Tab.6 The structure and water level of the Xiaoqing River

2.2.2 径流变异诊断分析与还现计算

采用式(1)-(5)对小清河流域径流列进行变异诊断分析，计算结果如图7所示。图7显示，曲线在1997年出现第一个交点，在2007年出现第2个交点。经查证，小清河于1996年开始进行河道整治工程，因此突变点为1997年具有合理性。1997年为径流的第一个突变点，且与2007年较为接近，故选取1997年为小清河径流变异点。从图7可以看出，变异点之后流量呈现逐年增大的趋势，因此主要研究变异点之前的流量序列，对其进行还现计算。

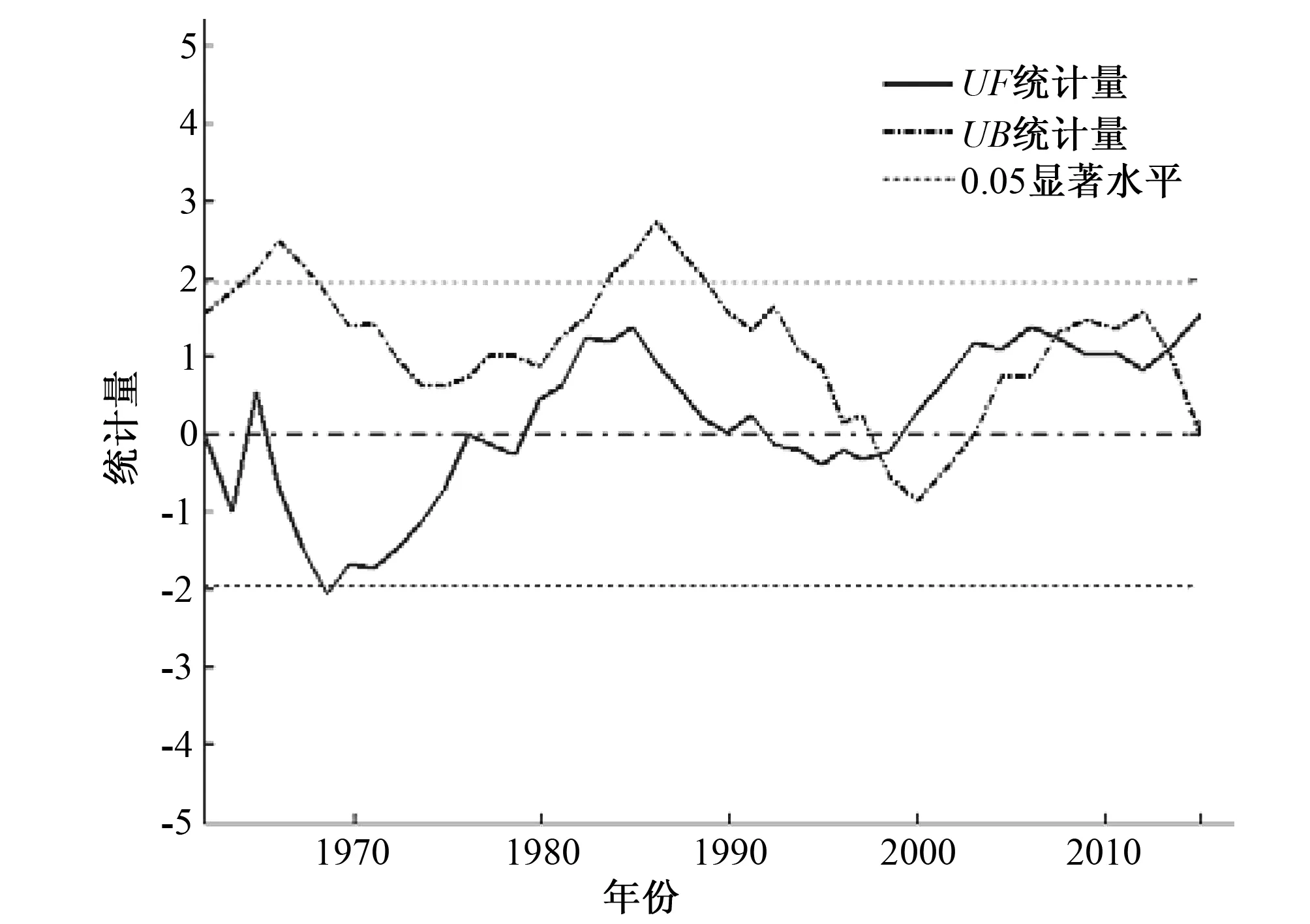
图7 小清河流域流量序列的Mann-Kendall法变异诊断结果Fig.7 Mann-Kendall variation diagnosis results of runoff series of Xiaoqing River

以第一个突变点后1997-2015年的降水-径流序列为基准，建立降水-径流关系曲线如图8所示。得到1997-2015年的降水-径流关系式为y=0.113 9x0.722 5，序列相关系数R2=0.600 4，曲线相关系数较低，表明小清河近年受人工补水等人为活动影响较大。应用此关系式对突变点前的径流进行模拟，结果如图9所示。图9显示，突变点之前由于河流未经补水，实测流量明显减小。因此，流量还原之后的生态基流分析，对恢复河流的天然水文情势具有一定意义。

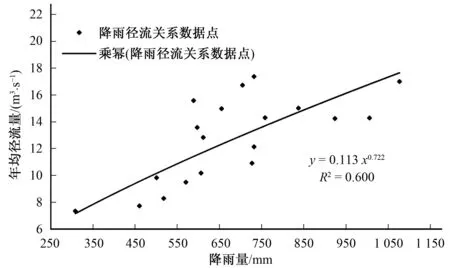
图8 小清河流域降水径流线性相关分析Fig.8 Linear correlation analysis of rainfall and runoff in Xiaoqing River Basin

2.2.3 典型年的Tennant法计算生态基流量

根据还现后的流量序列，计算得1962-2015年小清河平均流量为12.48 m3/s，比修正之前的流量提高了22.8%。通过选取突变点后典型年的方法，选取2007年实测逐月流量序列通过同倍比缩放至修正后的多年平均流量，再乘以对应流量百分数，与对应满足鱼类产育最低流量中的较大值，计算得经过还现分析的小清河逐月生态基流量，见表2、图10所示。从图表中可以看出原Tennant法计算值扁平化了小清河实际来水过程，典型年流量过程则体现了补水河流的用水特点，更易满足流域经济、社会、自然发展的需求。综合分析，利用流量还现技术改进的Tennant方法能够更好地反映城市河流的用水特点，结果较为合理。

图9 小清河实测及还现流量序列图Fig.9 TheMeasured flow and flow sequence diagram in Xiaoqing River

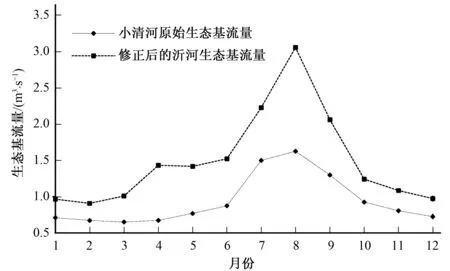
图10 修正前后的小清河逐月生态基流量曲线图Tab.10 The monthly ecological base flow curves before and after correction in Xiaoqing River

表3 修正前后的小清河逐月生态基流量计算表 m3/s

3 结 语

本文通过找出河流流量突变点，对不同类型的河流流量进行修正，同时通过选取典型年以及考虑鱼类产卵期最低流量对现行Tennant法进行改进，主要得出以下结论：

(1)以沂河为例，通过还原计算得出修正后的沂河平均流量为51.76 m3/s，比修正之前的流量提高了39.9%。通过修正的Tennant法解决了原始生态基流量多年平均流量值平坦化了沂河实际来水过程，典型年流量过程更好地体现了研究河段流量丰枯的季节性，更易满足“生态功能最小需水量”这一要求。综合分析，利用流量还原技术改进的Tennant方法能够更好地反映天然水文情势，有助于保障河流流速及水面宽度、水深度等生态栖息环境良性存在和发展。

(2)以小清河为例，通过还现计算得出修正后的小清河平均流量为12.48 m3/s，比修正之前的流量提高了22.8%，修正后的流量更符合小清河通航、排污的要求。从图表中可以看出原Tennant法中多年平均流量值削弱了小清河丰水期实际来水过程，改进方法能够更好地体现了补水区河段的用水特点，更易流域经济、社会、自然发展的需求。综合分析，利用流量还现技术改进的Tennant方法能够更好地反映城市河流的用水特点。

□

[1] 杨志峰, 尹 民, 崔保山.城市生态环境需水量研究----理论与方法[J]. 生态学报, 2005,25(3):389-396.

[2] 粟晓玲, 康绍忠. 生态需水的概念及其计算方法[J]. 水科学进展, 2003,14(6):740-744.

[3] Tharme R E. A global perspective on environmental flow assessment: emerging trends in the development and application of environmental flow methodologies for rivers[J]. River Research & Applications, 2003,19(5-6):397-441.

[4] 陈 菡, 邵东国, 吴俊校, 等. 广东省河道生态基流定量分析研究[J]. 南水北调与水利科技, 2011,9(1):92-95.

[5] 王西琴, 刘昌明, 杨志峰. 生态及环境需水量研究进展与前瞻[J]. 水科学进展, 2002,13(4):507-514.

[6] 韦雨婷, 逄 勇, 罗 缙. 清河干流生态基流计算分析[J]. 水资源与水工程学报, 2014,25(6):151-155.

[7] 郑红星, 刘昌明, 丰华丽. 生态需水的理论内涵探讨[J]. 水科学进展, 2004,15(5):626-633.

[8] 郑志宏, 张泽中, 黄 强,等. 生态需水量计算Tennant法的改进及应用[J]. 四川大学学报(工程科学版), 2010,42(2):34-39.

[9] 赵 阳,余新晓,郑江坤,等. 气候和土地利用变化对潮白河流域径流变化的定量影响[J]. 农业工程学报,2012,28(22):252-260.

[10] 天 霄, 付 强, 孟凡香, 等. 三江平原年降水量1959-2013年演变趋势及突变分析[J]. 中国农村水利水电, 2016,(9):201-204.

[11] 许 浩,雷晓辉,宋万祯,等. 水库建设运行对三岔河流域径流与洪水特征变化影响分析[J]. 中国农村水利水电,2016,(10):108-115.

[12] 金新芽. 径流还原实用方法研究[D]. 南京：河海大学,2006.

[13] 孙娟绒. 坪上水库径流还现计算分析[J]. 太原理工大学学报, 2005,36(5):589-592.

[14] 黄 强, 李 群, 张泽中, 等.计算黄河干流生态环境需水Tennant法的改进及应用[J]. 水动力学研究与进展(A辑), 2007,22(6):774-781.

[15] 杨裕恒, 曹升乐, 刘 阳, 等. 基于改进Tennant法的小清河生态基流计算[J]. 水资源与水工程学报, 2016,27(5):97-101.

[16] 徐宗学, 武 玮, 于松延. 生态基流研究:进展与挑战[J]. 水力发电学报, 2016,35(4):1-11.

[17] 田景环, 王 轶, 茹松楠, 等. 基于河流功能的Tennant法改进及其应用[J]. 人民黄河, 2011,33(11):100-102.

[18] 李昌文. 基于改进Tennant法和敏感生态需求的河流生态需水关键技术研究[D]. 武汉：华中科技大学, 2015.

[19] 林俊强, 彭期冬, 黄真理. 河流鱼类鱼卵运动的水力学研究进展[J]. 水利学报, 2015,46(7):869-876.

[20] 陈永柏, 廖文根, 彭期冬, 等.四大家鱼产卵水文水动力特性研究综述[J]. 水生态学杂志, 2009,30(2):130-133.

[21] 柏海霞, 彭期冬, 李 翀, 等. 长江四大家鱼产卵场地形及其自然繁殖水动力条件研究综述[J]. 中国水利水电科学研究院学报, 2014,12(3):249-257.

[22] 薛丽芳,谭海樵. 沂河流域水文特征变化及其驱动因素[J]. 地理科学进展, 2011,30(11):1 354-1 360.

[23] 谭永明.济南市小清河水质评价及环境需水量研究[D]. 济南：山东大学, 2009.