降雨条件下的滑坡-抗滑桩作用机理数值分析

徐水平，佟 新， 冯 永

(1.河南水利与环境职业学院，郑州 450008；2河南工业大学土木建筑学院，郑州 450001)

1 工程概况

1.1 工程概况

漳龙铁路于1998年4月8日正式动工，是国家1998年重点建设的工程，全长147.76 km，国家Ⅱ级铁路干线，总投资26.3 亿元，由铁道部、广东省和福建省合资修建的铁路。漳龙铁路广东段长99.78 km，投资为16.96 亿元，由广梅汕铁路有限责任公司负责建设和运营管理。

漳龙铁路茶阳车站位于铁路运营里程桩号漳龙线K160+350～K161+100，线路长0.76 km。而研究范围内现在由于人为的工程开挖及自然降雨，产生了一新滑坡。该滑坡的产生，直接导致了农田的鼓丘和凹陷，铁路轨道的位移和沉降，根据上述一系列岩土体滑动的痕迹，综合判断岩土体处于欠稳定～不稳定状态，有再次发生滑动可能性。

1.2 地层条件

根据勘察资料，场区内地层情况从地表起自上而下依次如表1所示。

1.3 滑坡体抗滑桩方案设计

为了确保车站及邻近建筑物的安全，按照初步确定的治理方案，在距离铁路红线7.5 m(距离铁路中心线32.5 m)处设置抗滑桩截面初定矩形桩，桩长最小值为35 m，最大值为42 m。要求抗滑桩工程的设计和施工必须安全可靠、整体稳定。

2 滑坡体-抗滑桩作用体系的三维分析

ABAQUS是一套功能强大的有限元软件，解决包括相对简

表1 土层力学性质参数

单的线性分析到工程复杂的非线性问题。

ABAQUS包括一个多样的、可模拟任意几何形状的单元库。拥有多种类型的材料模型库，可以模拟典型工程材料的性能，其中包括金属、高分子材料、复合材料、钢筋混凝土以及土壤和岩石等地质材料，这使得ABAQUS软件在处理岩土力学中复杂的非线性问题有其本身的优势。

2.1 土体本构模型选用及相关参数

本次模拟采用(非饱和土)岩土体选取Mohr-Coulomb(摩尔库伦)的本构模型，岩土体参数，见表1土层力学性质参数。

材料渗透系数与基质吸力的关系为：

kw=awkws/[aw+(bw(ua-uw))cv]

(1)

式中：ua为大气压力，由于与坡面接触，故取为0；kws是土体饱和时的渗透系数，取5.0×10-6m/s；aw、bw、cw是材料系数，分别取为1 000,0.01,1.7。

饱和度与基质吸力的关系为：

sr=si+(sn-si)as/[as+[as+(bs×(ua-uw))cs]

(2)

式中：Sr为饱和度；Si为残余饱和度，其值取为0.08；Sn为最大饱和度，取1；as、bs、cs是材料系数，取为1,0.000 05,3.5。

2.2 降雨模型

表2给出了气象部门规定的降雨量标准，本文中对降雨量的考虑参照表3选取，结合研究区实际情况，确定为4种降雨模式(表3及图1)。

表2 降雨量标准

图1 不同模式下的降雨过程曲线

编号降雨等级雨强/(mm·d-1)降雨历时/h降雨量/mm模式一无雨000模式二大雨402440模式三大暴雨10024150模式四大雨4072150

2.3 ABAQUS数值分析模型的建立

根据地质分析，边坡地质模型可概化为：杂填土、粉质黏土层、全风化砂岩、中风化绿帘石岩，三维地质模型范围平行于滑

体主轴方向为767 m(X轴方向)， 垂直于滑体主轴方向为450 m(Y轴方向)，垂直方向最高为105～273 m(Z轴方向，高程为0～167 m)，前后两面(滑坡移动方向)约束X、Y方向的位移，两侧面约束Y方向的位移，底面约束三个方向的位移，地表为自由面。考虑自重、地表荷载，计算工况为表4所列的工况，水位的作用采用程序中的渗流模式进行模拟。模拟过程中的土力学参数见表1。模型PAT是有犀牛软件生成的文件后导入国际通用有限元软件ABAQUS进行前处理分析的，计算模型如图2所示，共划分5 430个单元，24984个节点。

图2 岩土体三维计算模型

3 作用体系的三维分析结果

3.1 降雨作用下孔隙压力的结果分析

滑坡的孔隙水压力如图3所示，从图3中可以看出降雨入渗以后的孔压分布图跟初始的孔压分布有着明显的区别，降雨之前孔压随地层成线性分布，但之后岩土体顶部、中部及坡面以下一定范围内孔隙水压力明显升高，吸力区域减小，基质吸力也降低，同时，在降雨过程中图3(a)、(b)、(c)岩土体内部均未达到的饱和还都是负压力区，但在图4(d)中岩土体中部及坡面以下一定范围内孔隙压力已出现正值，说明此时滑坡体已出现饱和区。

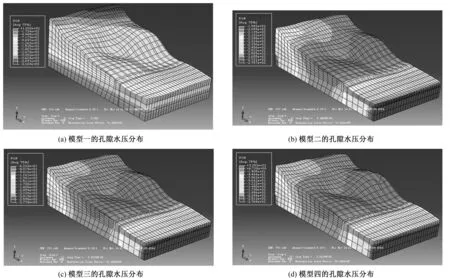
图3 各个模式下的孔隙水压分布图

现已检测点2作为研究对象，做出不同模式下J02点处的孔隙水压曲线，如图5。图5中模式一、二、三在24 h时孔隙水压分别为-2 108.1，-167.4，-143.2 kPa都还小于零，而模式四在72 h时为84.1 kPa已经大于零，由此可验证上述结论的正确性。

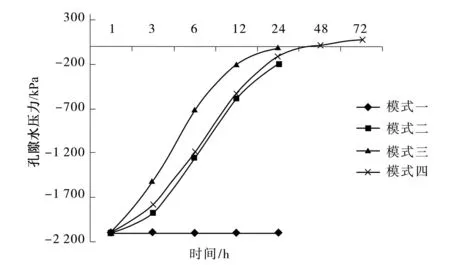
图4 各个模式下J02处的孔隙水压力曲线

同样，通过已有的检测点来看模式四各个监测点的孔隙水压力变化曲线，如图5。

图5 孔隙水压力变化曲线

通过图5同样可以验证图3得出的结论，图5中J02最后孔隙压力为84.1 kPa，已是正值，说明此时滑坡体已经饱和，随时都有可能出现滑坡危险的可能。

3.2 降雨作用下岩土体的位移分析

滑坡的水平位移如图3所示，在模式二下坡顶、坡底的水平位移较大，而随着降雨量的加大及降雨时长的增加，坡体水平位移的最大值由坡顶坡底逐渐过度到坡中水平位移最大说明降雨入渗后，岩土体的孔隙压力增加，有效应力减小导致坡体中部由于重力的影响而水平位移加大。同时可以看出坡中出现一定的膨胀，这主要是因为降雨导致滑坡体饱和度的增大而吸力有所降低同时有效应力减小，从而出现卸荷回弹现象。这也是为什么图3中坡中会先出现滑坡现象的原因。

图6 各个模式下的水平位移图

现在通过已有的检测点来看模式四各个监测点的水平位移变化曲线，如图7。

图7 水平位移变化曲线

通过图7可以看出，随着降雨量的加大及降雨时长的增加，J01水平位移由-0.005 9 m增加到-0.000 5 m，而J02由-0.017 8 m增加到0.059 8 m，J02位移增长率大于J01的增长率，由此可以验证图7坡体水平位移的最大值由坡顶坡底逐渐过度到坡中水平位移最大的结论，说明降雨入渗后，滑坡体的孔隙压力增加，有效应力减小导致坡体中部由于重力的影响而水平位移加大。

3.3 降雨作用对土拱效应的影响

滑坡的最大自主应力等值线云图如图8所示，从图8中可以看到随着降雨量的加大及降雨时长的增加，土拱效应作用逐渐减弱。这是因为随着降雨入渗土体孔压增大，饱和度也随着增加，岩土体的抗剪强度因有效应力减小导致土拱作用的减弱。

图8 各个模式下的最大主应变等值线

同样，在模型四选取模型左边第1、2根抗滑桩桩中心线垂直Y轴的剖面上(选取7个监测点)X方向应变作为研究对象，绘制出图9。

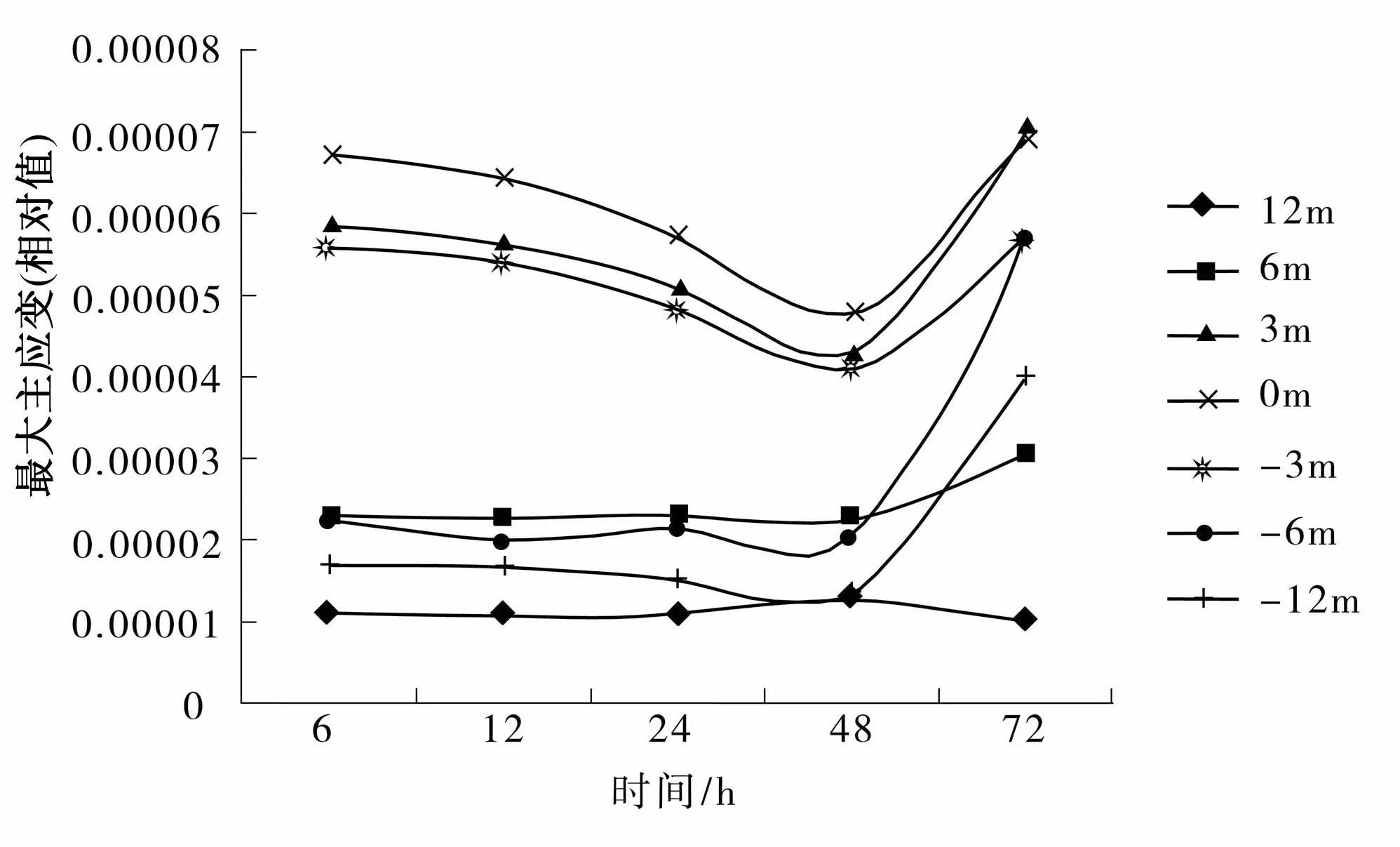
图9 最大主应变变化曲线

通过图9可以验证图8的结论：随着降雨量的加大及降雨时长的增加，12 m处的最大主应力等值线基本不变，而6 m处的受到了一定的影响说明应变拱半径最大可以到达6 m处，而12 m处基本不受影响。另外，从3、0、-3 m最大主应变变化曲线可以看出从6 h到48 h最大主应变曲线一直减小说明土拱效应起作用，到达48 h的时候土拱效应起最大作用随后应变急剧增加，此时土拱效应破坏。

3.4 三维空间的土拱效应分析

由图8可以看出由于受到土拱效应的影响,滑体的最大主应变在抗滑桩前后发生了显著的变化,在图10中可见桩后应力影响的范围自上而下逐渐减小,表明土拱效应的影响范围会随着滑体深度增加逐渐的变小，因此,在抗滑桩程实践中,应考虑到土拱效应随滑体的深度逐渐减弱的规律,并根据土拱作用的影响范围进行抗滑桩的设计。

图10 各个模式下抗滑桩处横切面最大主应变等值线

同样，在模型四下取计算模型抗滑桩处横切面左边第1、2根抗滑桩桩中心线垂直Y轴的剖面上(选取4个监测点)X方向应变作为研究对象，绘制出图11。

图11 最大主应变变化曲线

通过图11可以验证图10的结论：随着降雨量的加大及降雨时长的增加，-9 m处的最大主应力等值线基本不变，而0、-3、-6 m处在降雨到达48 h之前各个曲线是下走的趋势，这是因为土拱起作用的原因，而且各个斜率不一，0 m处最大而-6 m处最小可以，-9 m处基本不受影响，表明土拱半径在-6 m左右，在-9 m处土拱影响不到。另外，在从48 h之后各个曲线走势开始走高，说明此时土拱已经破坏，有随时发生滑坡灾害的可能。

4 结 语

(1)通过对降雨作用下孔隙压力结果的分析得出：降雨入渗后的孔压分布跟初始孔压分布有着明显的区别，降雨之前孔压随地层成线性分布，但之后坡面以下一定范围内孔隙水压力出现明显变化，吸力区域减少，基质吸力降低。同时，在降雨过程中，非饱和土会有从负压力区转变到正压力区，当到一定程度时随时可能会发生滑坡地质灾害。

(2)通过对降雨作用下岩土体位移分析得出：随着降雨量的加大及降雨时长的增加，岩土体的孔隙压力增加，有效应力

减小导致滑坡体由于重力的影响而水平位移加大。同时，在实际的岩土体会出现一定的膨胀现象，这主要是因为降雨导致边坡饱和度增大而地质吸力有所降低，得有效应力减小从而出现卸荷回弹的现象。

(3)通过降雨作用对土拱效应的影响分析得出：随着降雨入渗，孔隙压力增大，饱和度随着增加，岩土体的抗剪强度因有效应力减小导致土拱效应减弱。

(4)桩后应力影响的范围自上而下逐渐减小,表明土拱效应的影响范围会随着滑体深度增加而逐渐减小。

□

[1] 中国气象局,气象预报发布与传播管理办法[Z].

[2] 邹厂电,陈生水.抗滑桩工程的整体设计方法及其优化数值模型[J].岩土工程学报,2003,25(1): 11-17.

[3] 娄奕红,彭俊生.桩土相互作用的砂箱模型试验及计算分析m.西南交通大学学报.2003,28(2):164-168.

[4] 魏作安,周永昆,万玲.抗滑桩与滑体之间土拱效应的理论分析[J].力学与实践,2010,32(3):57-61.

[5] 闫金凯,殷跃平,门玉明.微型桩单桩加固滑坡体的模型试验研究[J].工程地质学报.2010,17(5): 669-675.

[6] Chen L T, Poulos H G. Piles subjected to lateral soil movements[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 1997,123(9):802-811.

[7] Pieter A. Vermeer, Ankana Punlor,Nico Ruse. Arching effects behind a soldier pile wall[J].Computersand Geotechnics, 2001,(28):379-396.

[8] Jinoh Won, Kwangho You, Sangseom Jeong, Sooil Kim. Coupled effects in stability analysis of pile-slope systems. Computers and Geoteclmics, 2005,32:304-315.

[9] Ausilio E, Conie E, Dente G.Stability analysis of slopes reinforced with piles [J]. Compeuter and Geotechnics Volume, 2001,28(8):591-611.

[10] 杨明,姚令侃,王广军.抗滑桩宽度与桩间距对桩间土拱效应的影响研究[J],2007,29(10):1 477-1 482.

[11] 杨明.桩土相互作用机理及抗滑加固技术[D].成都:西南交通大学,2008.

[12] 熊良宵,李天斌.土拱效应在抗滑桩工程中的应用[J].防灾减灾工程学报,2005,25(3):275-277.