基于颗粒流方法的土体压密注浆细观机理

周子龙，赵云龙，陈钊，杜雪明，吴志波



基于颗粒流方法的土体压密注浆细观机理

周子龙1，赵云龙1，陈钊2，杜雪明1，吴志波1

(1. 中南大学资源与安全工程学院，湖南长沙，410083；2. 广西交通规划勘察设计研究院，广西南宁，530029)

为揭示高压注浆过程中浆液的扩散规律与压密效果，运用颗粒流方法对不同注浆压力、不同土体黏结力、不同土体摩擦因数下浆泡半径以及注浆效果的细观规律和机理进行分析。采用颗粒流fish语言建立注浆过程模型，采用伺服机制施加不同注浆压力模拟注浆过程。研究结果表明：随着注浆压力增大，注浆点周围的土体不断被压缩，孔隙率变小，且0.5 m内土体最易受影响，变形速率最快；与此同时，注浆压力增大，周围土体的附加应力不断增加；对于特定的土体条件，都存在1个最佳注浆压力；土体颗粒之间的黏结力对于浆液扩散的影响较大；土体黏结力较小时，注浆后浆泡半径随注浆压力增大变化明显，但当黏结力较大时，浆泡尺寸基本不随注浆压力变化，即土体黏结力较大时，压密注浆效果大大削弱；土体颗粒之间摩擦因数的变化对注浆效果影响不大。

压密注浆；颗粒流；细观机理

注浆技术是岩土工程中一种极为重要的施工方法，被广泛应用于矿山充填、巷道围岩维护、公路路基处理等方面，按照浆液对土体的作用机理可分为压密注浆、劈裂注浆、渗透注浆等[1]。其中压密注浆是目前应用最广泛的一种注浆方法，该方法的工程效果已受到工程界的广泛认可[2−7]，但人们对压密注浆过程中浆液与土体的细观作用机理还不十分清楚。一些学者对压密注浆进行了研究，如：邹金峰等[8]将注浆过程视为无限土体中的圆孔扩展问题，从能量守恒的角度，推导出极限注浆压力的理论解答；巨建勋[9]建立了压密注浆的柱形扩散模型，并采用有限元的方法对压密注浆的作用机理进行模拟，得到浆液的扩散半径以及极限注浆压力的变化规律；邹健等[10−11]研究了压滤效应对压密注浆的影响，改善了传统的压密注浆扩散理论；唐智伟等[12]采用FLAC3D分析了压密注浆对地层的抬升机制。整体上看，现有研究主要集中在理论和数值分析2个方面，其中理论解析方面均采用向周围土体施加各向同性膨胀力的方法，但在实际压密注浆过程中，浆液与土体存在不均匀接触；数值分析方面则未考虑浆液与土体的内部作用过程，以致一些微观机理未能有效揭示。离散元法是近几年兴起的一种岩土数值模拟方法，用其建立的模型可以较好地体现岩土介质的内部颗粒组成，既能模拟颗粒的流动性，又可实现土粒与土粒、浆液与土粒间的不均匀接触和相互侵入。为此，本文作者利用该方法对不同注浆压力作用下浆体对土体压密的动态过程和规律进行研究，以便揭示其内在规律和机理。

1 压密注浆作用机理

压密注浆法是指将较稠的浆液通过钻孔强行挤向土体，并在注浆点附近形成近似球形或者柱形浆泡，通过浆泡来挤压被注载体邻近土体的一种施工方法[7](见图1(a))。在浆泡形成过程中，浆泡的半径随着注浆压力的增大而增大，如图1(b)中曲线I所示；同时，对于给定的上覆土层，导致土层上抬所需的注浆压力与浆泡的半径或者水平投影面积有关，两者之间的关系如图1(b)中的曲线Ⅱ所示。

通过现场观测发现，土体压密注浆后在距离浆泡0.3~1.8 m处有挤压作用，在此范围内，距离浆泡越远，挤密作用越弱。在不均匀地基中，浆泡呈现不规则形状，浆液总是挤向不均地基中的薄弱土区，从而使该处土体增强。

(a) 压密注浆示意图；(b) 应力变化

Ⅰ—注浆压力与浆泡半径的关系；Ⅱ—抬升压力与浆泡半径的关系。

图1 压密注浆示意图和应力变化

Fig. 1 Sketch and stress variation of compaction grouting

2 注浆模型与分析方案

目前人们对注浆的数值分析研究并不多，王立中等[13−15]对注浆模拟进行了研究，但从土体颗粒与浆液颗粒相互作用的细观机理角度进行的分析较少。本文采用离散元颗粒流程序PFC2D[16−17]，将注浆材料与土体看作由若干细小颗粒组成，通过颗粒间的相互接触模拟浆液与土体之间的相互作用。

2.1 模型与计算参数选取

注浆所用浆液的参数以及土体颗粒的参数选取如下：最大粒径为5 mm；最小粒径为5 mm；摩擦因数为0.001；颗粒法向接触刚度为6.5 MN/m；颗粒法向刚度与切向刚度比为1.0。土体参数见表1。

土体模型的长×宽为16 m×10 m，注浆点的深度为6.0 m，注浆孔的直径为100 mm。生成的模型如图2(a)所示，注浆点局部放大图如图2(b)所示。

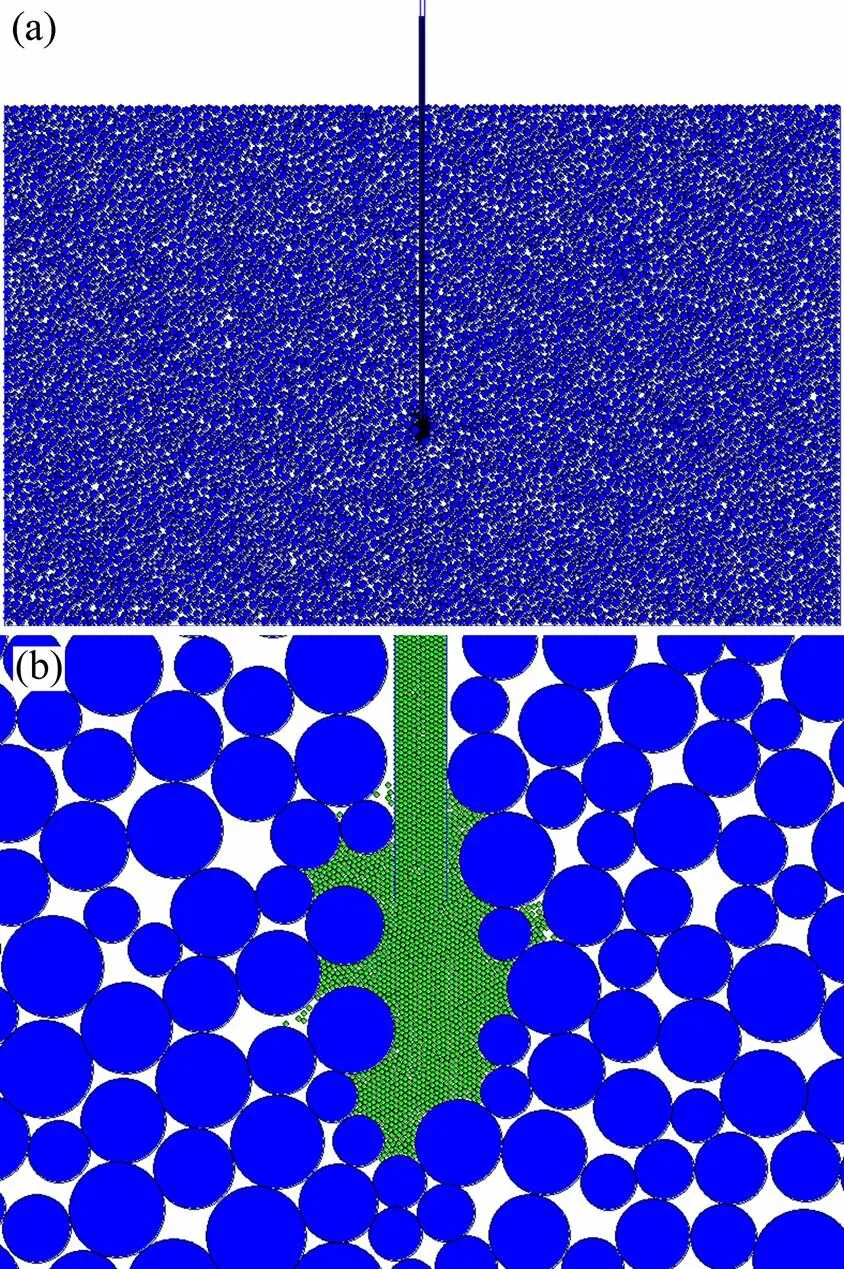
(a) 整体图；(b) 注浆点局部图

2.2 分析方案

通过软件内置的Fish语言，实现如图2所示的注浆模型，同时在注浆孔周围布置测量圆，通过监测相关结果，从而得出不同的条件下浆泡的半径、注浆点周围土体孔隙率以及周围土体应力等参数的变化规律。具体分析方案如下。

1) 不同注浆压力影响。选取注浆压力为0.2，0.5，0.7和1.0 MPa，土体参数选取表1中方案1，分析不同注浆压力作用下浆泡半径、周围土体应力以及孔隙率的变化。

2) 不同土体颗粒黏结力影响。注浆压力选取0.7 MPa，土体参数选取表1中方案2，分析随着土体颗粒之间黏结力的增加，浆泡半径、周围土体应力以及孔隙率的变化。

3) 不同土体颗粒摩擦因数影响。注浆压力选取0.7 MPa，土体参数选取表1中方案3，分析随着土体颗粒之间摩擦因数的增加，浆泡半径、周围土体应力以及孔隙率的变化。

3 不同条件下注浆结果分析

3.1 注浆压力对压密注浆的影响

利用注浆浆液参数、表1中方案1的浆液和土体参数，对0.2，0.5，0.7和1.0 MPa等注浆压力下的孔隙度进行分析，可获得注浆点周围土体孔隙率的变化，从而反映土体被压密的程度。图3所示为不同注浆压力下土体孔隙率变化曲线。从图3可以看出：在注浆点0.5 m半径范围内，土体孔隙率变化最明显；随着注浆时步增加，土体孔隙率不断减小，但当注浆时步大于2.0×105时，孔隙率基本保持不变，即注浆完成；在离注浆点较远的1.0 m和1.5 m半径范围内，当注浆压力较小时，土体孔隙率受影响较小；当注浆压力大于0.7 MPa时，该区域土体受到较大压密作用。不过，当注浆时步大于2.0×105后，土体孔隙率趋于恒定，意味着注浆基本完成。从土体孔隙率的变化规律可见：当注浆压力较小时，由于浆液与土体接触面积较小，土体被压密的范围较小；随着注浆压力增大，浆液颗粒与土体颗粒的接触面积增大，浆液颗粒不断挤压土体颗粒，使得周围土体发生破坏并被不断压缩，且范围越来越大；每个注浆压力都对应1个最佳作用半径，如在本文的土体参数条件下，当注浆压力小于0.5 MPa时，最佳注浆半径为0.5 m左右；当注浆压力为1.0 MPa时，最佳注浆半径可达1.5 m。

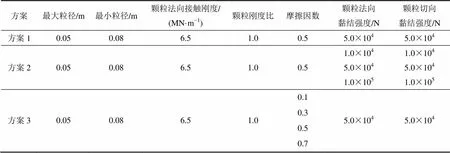
表1 土体参数

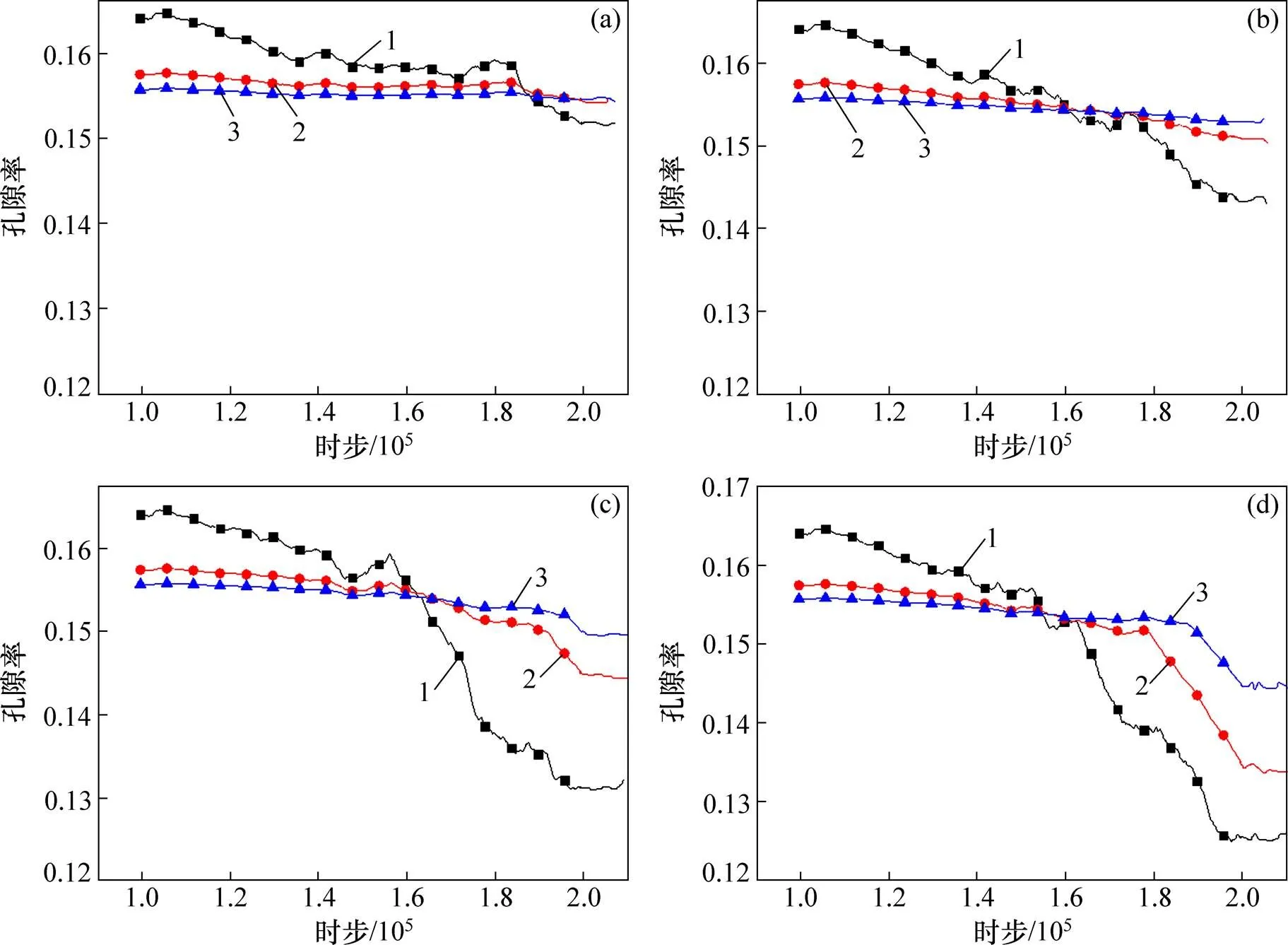
注浆压力/MPa：(a) 0.2；0.5；(c) 0.7；(d) 1.0

以注浆点为中心的半径/m：1—0.5；2—1.0；3—1.5。

图3 不同注浆压力下周边土体孔隙率的变化

Fig. 3 Porosity changes of surrounding soil under different grouting pressures

在压密注浆过程中，周围土体应力的变化也能从另一方面反映土体的压密程度。离散元法可以通过测量圆监测周围土体应力的变化，得出周围土体应力的变化规律。表2所示为不同注浆压力下注浆点周围土体的应力分布情况。由表2可以看出：随着注浆压力增加，以注浆点为中心0.5 m半径范围内土体的应力变化最明显，1.0 m内应力变化次之，1.5 m内应力变化最小，已趋于原始土应力。

随着注浆进行，周围土体被不断压密并产生应力，浆液的持续注入受到阻止并在注浆点附近形成浆泡。图4所示为不同注浆压力下注浆完成后浆泡形态。从图4可以看出：随着注浆压力增大，浆泡的半径不断增大；当注浆压力为0.2 MPa时，浆液主要集中在注浆管附近，并没有明显的浆泡出现，说明当注浆压力较小时，浆液挤压土体作用较小，浆液仅在注浆口附近局部渗入土体；当注浆压力大于0.5 MPa时，出现明显的不规则浆泡，这与张忠苗等[18]进行室内压密注浆试验得出的浆泡形状一致。同时，随着注浆压力增大，浆泡半径增大。图5所示为浆泡半径与注浆压力之间的关系曲线，该曲线变化趋势与图1(b)中的曲线Ⅰ变化趋势一致。

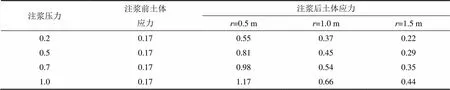
表2 周围土体附加应力的变化

注：为距离注浆点的距离。

3.2 土体黏结力对压密注浆的影响

利用注浆浆液参数、表1中方案2的土体参数，注浆压力选取0.7 MPa进行分析，获得颗粒黏结强度为1.0×104，5.0×104和1.0×105N时土体中浆泡半径变化规律，如图6所示。

注浆压力/MPa：(a) 0.2；(b) 0.5；(c) 0.7；(d) 1.0

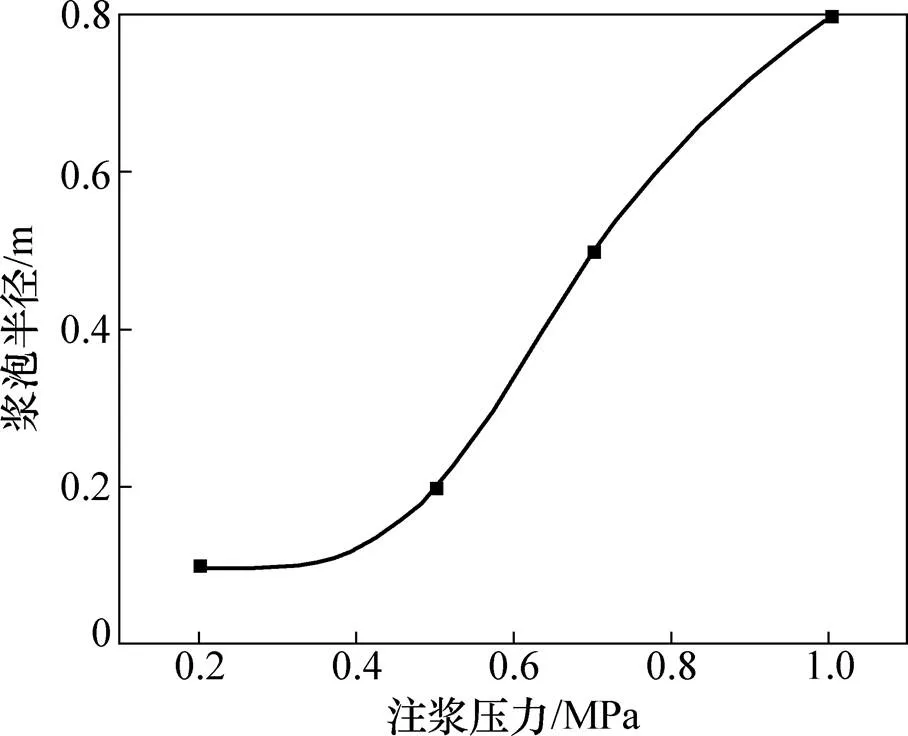
图5 浆泡半径与注浆压力的关系

由图6可以看出：土体之间的黏结力对于注浆的效果影响较明显；在相同注浆压力作用下，当土体之间的黏结力较小时，浆泡的半径较大，如图6(a)所示；当土体之间的黏结力较大时，浆液主要集中在注浆管附近，没有明显的浆泡出现，如图6(c)所示。

对于不同土体颗粒黏结力的情况，周围土体孔隙率的变化如图7所示。从图7可以看出：当土体黏结力较小时，压密注浆效果较好；当土体黏结力较大时，对压密注浆不利。以注浆压力为0.7 MPa时为例，土体黏结力为1.0×104N，在注浆点近区(0.5 m半径点)土体孔隙率从0.15左右降低为0.12左右；但当土体黏结力增大到1.0×105N时，即使在注浆点近区，土体的孔隙率仍基本不受影响，即注浆效果大大削弱。

3.3 土体颗粒间摩擦因数对压密注浆的影响

利用注浆浆液参数、表1中方案3的土体参数，选取注浆压力0.5 MPa进行分析，可获得土体颗粒摩擦因数为0.1，0.3，0.5和0.7时注浆过程中土体参数的变化情况，见图8。从图8可以看出：在不同土体颗粒摩擦因数下，注浆完成后浆泡形态区别不明显，浆泡半径为0.5 m左右。这说明颗粒之间的摩擦因数对于压密注浆效果影响不大。不同土体颗粒摩擦因数条件下注浆后土体孔隙率和应力的变化情况如图9和图10所示。

从图9和图10可以看出：当土体颗粒之间摩擦因数发生变化时，周围土体的孔隙率和应力均在某一数值附近小幅度波动，这进一步说明土体颗粒之间的摩擦因数对于浆液的压密作用影响较小。摩擦因数的增加使得浆液颗粒与土体颗粒之间的摩擦力增加，但一般来说，注浆压力相对于摩擦力来说较大，因此，这种摩擦力在注浆过程中发挥的作用有限，这与孙峰 等[14]进行土体劈裂注浆过程的细观模拟研究所得出的结论相同，即摩擦因数对劈裂缝形成时期的影响规律不是很明显，其原因主要是土体峰值以前的强度特性是由颗粒间的接触连接强度决定；而颗粒间的摩擦因数只影响峰值后的变化趋势。

土体黏结力/N：(a) 1.0×104；(b) 5.0×104; (c) 1.0×105

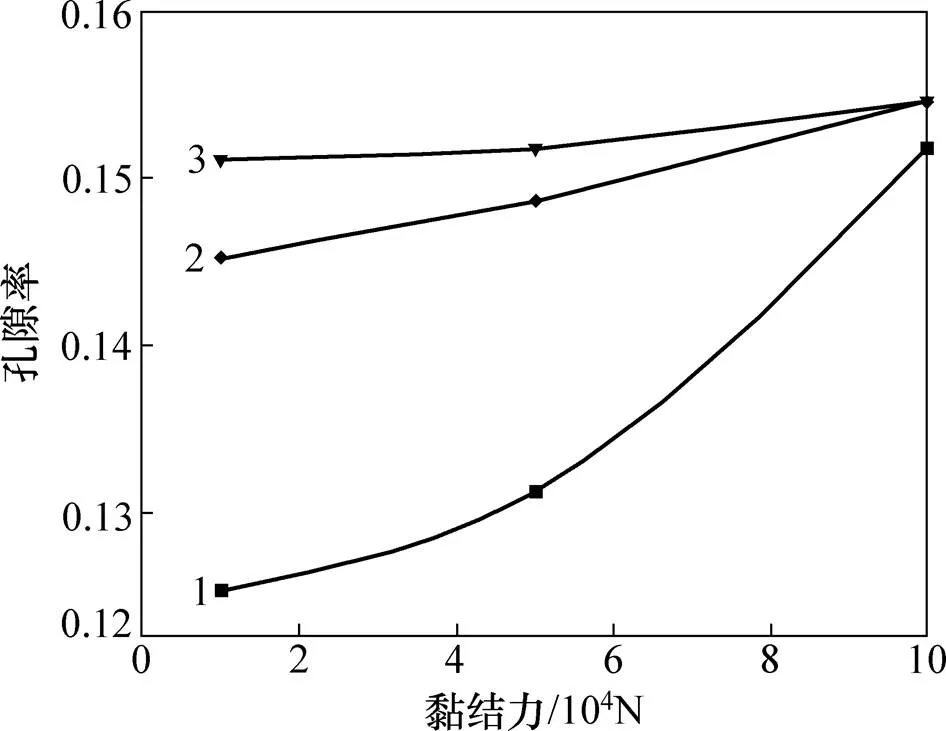
以注浆点为中心的半径/m：1—0.5；2—1.0；3—1.5。

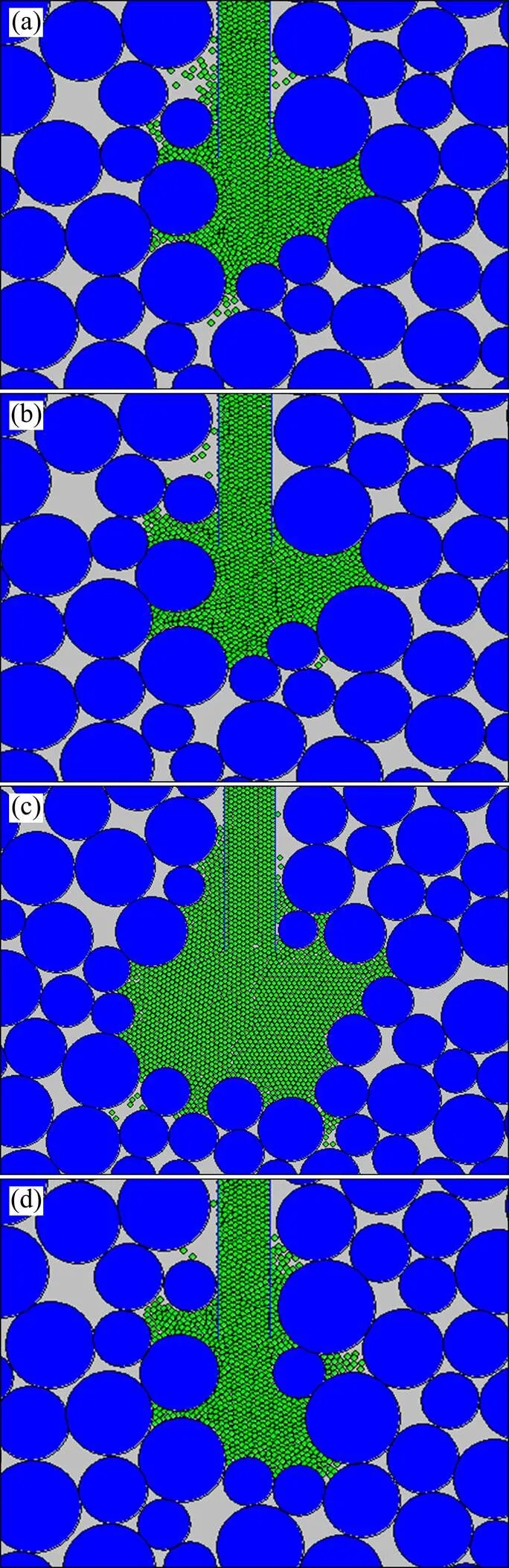
摩擦因数：(a) 0.1；(b) 0.3；(c) 0.5；(d) 0.7

以注浆点为中心的半径/m：1—0.5；2—1.0；3—1.5。

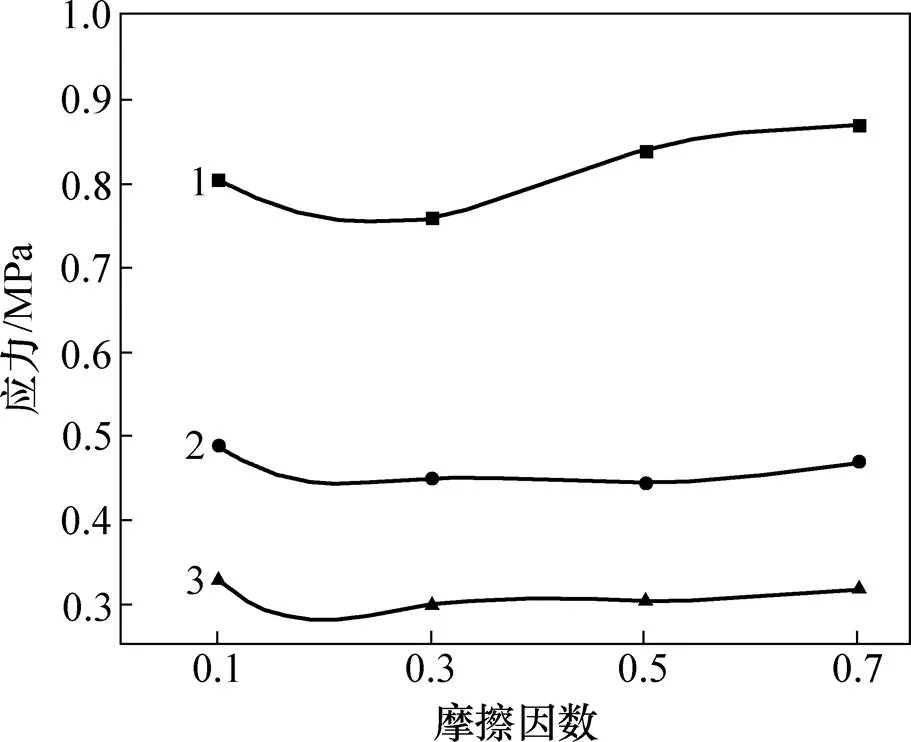
以注浆点为中心的半径/m：1—0.5；2—1.0；3—1.5。

4 结论

1) 注浆压力是影响压密注浆的重要因素。随着注浆压力增加，土体被压密的范围逐渐扩大，土体中的附加应力提高，浆泡半径随着注浆压力增大而增大。

2) 土体黏聚力对于注浆的效果影响明显。当土体黏结力较小时，浆液的作用范围较大；当土体黏结力较大时，压密注浆效果受到较大影响。

3) 不同土体颗粒摩擦因数对注浆效果几乎没有影响。当土体颗粒之间摩擦因数变化时，周围土体的孔隙率和应力仅在某一数值附近小幅度波动。

[1] 杨米加, 陈明雄. 注浆理论的研究现状及发展方向[J]. 岩石力学与工程学报, 2001, 20(6): 839−841. YANG Mijia, CHEN Mingxiong. Current research state of grouting technology and its development direction future[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(6): 839−841.

[2] 李兴尚, 许家林, 朱卫兵, 等. 条带开采垮落区注浆充填技术的理论研究[J]. 煤炭学报, 2008, 33(11): 1205−1210. LI Xingshang, XU Jialin, ZHU Weibing, et al. Theoretical study on the backfill grouting in caving area with strip mining[J]. Journal of China Coal Society, 2008, 33(11): 1205−1210.

[3] 李为腾, 王琦, 李术才, 等. 深部顶板夹煤层巷道围岩变形破坏机制及控制[J]. 煤炭学报, 2014, 39(1): 47−56. LI Weiteng, WANG Qi, LI Shucai, et al. Deformation and failure mechanism analysis and control of deep roadway with intercalated coal seam in roof[J]. Journal of China Coal Society, 2014, 39(1): 47−56.

[4] 吴顺川, 金爱兵, 高永涛.袖阀管注浆技术改性土体研究及效果评价[J]. 岩土力学, 2007, 28(7): 1353−1358. WU Shunchuan, JIN Aibing, GAO Yongtao. Studies of sleeve-valve-pipe grouting technique and its effect on soil reinforcement[J]. Rock and Soil Mechanics, 2007, 28(7): 1353−1358.

[5] 秦前波, 方引晴, 骆行文, 等. 深层高压注浆加固古滑坡滑动带试验及效果分析[J]. 岩土力学, 2012, 33(4): 1185−1190. QIN Qianbo, FANG Yinqing, LUO Xingwen, et al. Test and analysis of effect of applying deep high pressure grouting method on stabilizing sliding zone of ancient debris landslide[J]. Rock and Soil Mechanics, 2012, 33(4): 1185−1190.

[6] 朱宝龙, 胡厚田, 张玉芳, 等. 钢管压力注浆型抗滑挡墙在京珠高速公路 K108 滑坡治理中的应用[J]. 岩石力学与工程学报, 2006, 25(2): 399−406. ZHU Baolong, HU Houtian, ZHANG Yufang, et al. Application of steel-tube bored grouting anti-sliding retaining wall to treatment of landslide K108 in Bejing Zhuangtai expressway[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(2): 399−406.

[7] 刘永文, 王新刚, 冯春喜, 等. 注浆材料与施工工艺[M]. 北京: 中国建材工业出版社, 2008: 20−25. LIU Yongwen, WANG Xingang, FENG Chunxi, et al. Grouting material and construction technology[M]. Beijing: China building Materials Press, 2008: 20−25.

[8] 邹金锋, 李亮, 杨小礼, 等. 压密注浆的能量分析方法[J]. 岩土力学, 2006, 27(3): 475−478. ZOU Jinfeng, LI Liang, YANG Xiaoli, et al. Method of energy analysis for compaction grouting[J]. Rock and Soil Mechanics, 2006, 27(3): 475−478.

[9] 巨建勋. 土体压密注浆机理及其抬升作用的研究[D]. 长沙: 中南大学地学与环境工程学院, 2007: 36−50. JU Jianxun. Studies of soil compaction grouting mechanism and Lifting effect [D]. Changsha: Central South University. School of Geoscience and Environmental Engineering, 2007: 36−50.

[10] 邹健, 张忠苗. 考虑压滤效应饱和黏土压密注浆球孔扩张理论[J]. 哈尔滨工业大学学报, 2012, 43(12): 119−123. ZOU Jian, ZHANG Zhongmiao. Spherical cavity expansion theory of compaction grouting in saturated clay considering pressure filtration[J]. Journal of Harbin Institute of Technology, 2012, 43(12): 119−123.

[11] 张忠苗, 邹健, 何景愈, 等. 考虑压滤效应下饱和黏土压密注浆柱扩张理论[J]. 浙江大学学报(工学版), 2012, 45(11): 1980−1984. ZHANG Zhongmiao, ZOU Jian, HE Jingyu, et al. Cavity expansion theory of compaction grouting in saturated clay considering pressure filtration[J]. Journal of Zhejiang University (Engineering Science), 2012, 45(11): 1980−1984.

[12] 唐智伟, 赵成刚. 注浆抬升地层的机制: 解析解及数值模拟分析[J]. 岩土力学, 2008, 29(6): 1512−1516. TANG Zhiwei, ZHAO Chenggang. Mechanisms of ground heave by grouting and analytical solutions & numerical modeling[J]. Rock and Soil Mechanics, 2008, 29(6): 1512−1516.

[13] 王立中. 柔性管加筋注浆新技术试验及应用研究[D]. 长沙: 中南大学土木建筑学院, 2008: 62−75. WANG Lizhong. Application of new technologies and experiment reinforced flexible tube grouting[D]. Changsha: Central South University. School of Civil Engineering and Architecture, 2008: 62−75.

[14] 孙锋, 张顶立, 陈铁林, 等. 土体劈裂注浆过程的细观模拟研究[J]. 岩土工程学报, 2010, 32(3): 474−480. SUN Feng, ZHANG Dingli, CHEN Tielin, et al. Meso-mechanical simulation of fracture grouting in soil[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(3): 474−480.

[15] 袁敬强, 陈卫忠, 谭贤君, 等.软弱地层注浆的细观力学模拟研究[J]. 岩土力学, 2011, 32(2): 653−659. YUAN Jingqiang, CHEN Weizhong, TAN Xianjun, et al. Mesomechanical simulation of grouting in weak strata[J]. Rock and Soil Mechanics, 2011, 32(2): 653−659.

[16] Itasca Consulting Group Inc. PFC2D user’s manual (version3.1)[M]. Minneapolis, MN: Itasca Consulting Group Inc., 2006: 49−57.

[17] POTYONDY D O, CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329−1364.

[18] 张忠苗, 邹健, 贺静漪, 等.黏土中压密注浆及劈裂注浆室内模拟试验分析[J]. 岩土工程学报, 2009, 31(12): 1818−1824. ZHANG Zhongmiao, ZOU Jian, HE Jingyi, et al. Laboratory tests on compaction grouting and fracture grouting of clay[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(12): 1818−1824.

(编辑 陈灿华)

Meso-mechanism of compaction grouting in soil based on particle flow method

ZHOU Zilong1, ZHAO Yunlong1, CHEN Zhao2, DU Xueming1, WU Zhibo1

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;2. Guangxi Communications Planning Surveying and Designing Institute, Nanning 530029, China)

In order to reveal the diffusion law and consolidation effect in high pressure slurry of compaction grouting, the particle flow method was used to analyze the meso-mechanism of grouting in consideration of different grouting pressures, soil cohesion force and friction coefficient. With particle flow fish language, the grouting model was established, and the servo mechanism was used to apply different grouting pressures to simulate the grouting process. The results show that with the increase of grouting pressure, soil around the grouting point is compressed gradually, and the soil porosity becomes smaller. The soil within radius of 0.5 m around the grouting point is the most sensitive to the grouting pressure and deforms most rapidly. The additional stress of the soil around the grouting point increases with the increase of the grouting pressure. There is an optimum grouting pressure for a specific soil condition in practice. The cohesion force of soil particles has significant influence on the slurry diffusion. When the soil cohesion force is small, the radius of grouting bulbs increases with the increase of grouting pressure. When the soil cohesion force is big, grouting pressure has little effect of on the grouting bulb size. The effect of compaction grouting is undermined in this situation greatly. The friction coefficient of soil particles has little influence on the grouting performance.

compaction grouting; particle flow; meso-mechanism

10.11817/j.issn.1672−7207.2017.02.026

U459.2

A

1672−7207(2017)02−0465−08

2016−02−08；

2016−04−12

国家重点基础研究发展计划(973计划)项目(2015CB060200)；国家自然科学优秀青年基金资助项目(51322403)；广西省交通厅项目(2015年)(Project(2015CB060200) supported by the National Basic Research Development Program(973 Program) of China; Project (51322403) supported by the National Natural Science Foundation for Outstanding Young Scientists of China; Project(2015) supported by Traffic Department of Guangxi Zhuang Autonomous Region)

周子龙，博士生导师，从事采矿与岩土工程灾害防治研究；E-mail：zlzhou@csu.edu.cn