核磁共振陀螺用高均匀磁场线圈设计方法

王春娥,秦 杰

(北京自动化控制设备研究所,北京100074)

核磁共振陀螺用高均匀磁场线圈设计方法

王春娥,秦 杰

(北京自动化控制设备研究所,北京100074)

核磁共振陀螺代表了新一代高精度、微小型陀螺的发展方向之一,随着陀螺体积的降低,磁屏蔽层与磁场线圈随之减小,且二者贴合更加紧密,高导磁性的磁屏蔽层及低导磁性的空气介质交错分布,改变了线圈的磁通路径,导致线圈的磁场均匀性下降,制约了陀螺精度的提高。针对这一问题,提出了磁场等效增益系数,模拟磁屏蔽边界对线圈磁场的影响,据此建立了磁屏蔽边界条件下高均匀磁场线圈模型,优化了线圈参数。对所设计线圈的磁场均匀性进行了测试,表明该设计方法可以得到磁屏蔽边界条件下高均匀磁场线圈,可为发展微小型、高精度的核磁共振陀螺高均匀磁场线圈设计方法提供参考。

核磁共振陀螺;磁场线圈;磁屏蔽边界;磁场均匀性

0 引言

核磁共振陀螺基于量子调控技术的前沿研究进展,具有高精度、小体积、低功耗、对加速度不敏感等优点[1-2],是新一代陀螺技术的典型代表[3]。该陀螺有望为无缝导航定位领域带来革命性新产品[4],对国民经济发展与国防建设具有重要意义。

核磁共振陀螺基于核自旋磁共振频率在惯性空间的不变性测量角运动,采用光场、磁场等对核自旋系综的综合操控实现[5]。三维磁线圈与磁屏蔽层是磁场操控的主要执行元件[6]。随着核磁共振陀螺向微小型方向发展,磁屏蔽层与三维磁场线圈随之减小,且二者贴合更加紧密,以减少空间浪费。因此,在微小型核磁共振陀螺中,三维磁线圈所处位置及内侧为低磁导率的空气介质,而外侧为高磁导率的软磁屏蔽材料[7]。当在线圈中施加控制电流时,电流磁场需经过多种不同磁导率的磁介质而形成磁通回路,不同磁介质分界面上产生的磁路折射使线圈中心区域总磁场的方向及大小发生变化,导致线圈磁场分布发生畸变[8-9],磁场均匀性大幅降低。因此,如何实现小体积、高均匀性的磁场线圈设计及优化,已经成为发展微小型、高精度核磁共振陀螺亟需解决的关键科学问题之一。

螺线管线圈为最常用的磁场线圈形式[10-11],为提高线圈磁场均匀性,现已发展出包括亥姆霍兹线圈、巴克尔线圈、马鞍形线圈等[12-15]在内的多种线圈形式及设计方法,但各型线圈均以自由边界条件为设计约束,应用中仅当线圈周围不存在导磁性物质时磁场均匀性才可达到理论设计值。将线圈置于磁屏蔽边界条件下时,线圈磁场均匀性仍无法满足设计需求。

本文提出一种基于线圈磁场等效增益系数的高均匀磁场线圈设计方法,利用等效增益系数将非均匀磁介质对线圈磁场的影响进行均匀化处理,结合单一磁介质下线圈磁场求解析模型,建立多匝线圈在均匀化处理后边界条件作用下的磁场模型,在此基础上进行磁场高均匀性设计及优化,以实现高均匀磁场线圈设计。

1 线圈磁场等效增益系数模型

定义线圈磁场等效增益系数为线圈分别处于磁屏蔽边界条件下及自由边界条件下时,在线圈内部特定区域产生的磁场比值,即

(1)

其中,Bp为磁屏蔽边界下待求区域线圈产生的总磁场,Bf为自由边界下待求区域线圈产生的总磁场。由于线圈一般由多匝导线串联组成,各匝导线在磁屏蔽层内的位置不同导致其磁场等效增益系数不同。因此,建立模型时可构建单匝线圈在磁屏蔽层内不同位置时的等效增益变化,为整个线圈磁场模型的建立提供基准。

根据线圈磁场等效增益系数定义,首先分别建立单匝线圈处于不同位置时在自由边界及磁屏蔽边界下产生的磁场,磁屏蔽层内线圈及待求磁场区域的相对位置关系如图1所示,并在待求磁场区域取典型点O、A及B作为磁场监测点。

图1 磁屏蔽层内线圈及待求磁场区域示意图Fig.1 The sketch map of the coil and the magnetic area to be solved in the magnetic shielding layer

1.1 磁屏蔽边界下线圈磁场求解

由于磁屏蔽层对线圈磁场的影响难以通过解析模型直接求解,因此建立磁屏蔽边界下线圈磁场的有限元模型,经网格剖分、物理属性设置后进行磁场求解。

基于有限元方法建立磁屏蔽层及单匝线圈模型,结合磁屏蔽层结构尺寸选择合适的网格形状及大小,可得到磁屏蔽层的网格剖分如图2所示。

笔者认为课例打磨类教研论文的撰写一定要清晰的呈现前后三次不同的教学设计，可以按照教学环节呈现，也可以整体呈现.如果按照教学环节呈现(以“分式的基本性质(1)”的磨课为例，详见文[2])，笔者认为可以对每一个教学环节以“首次试教、再次试教、最后试教”的形式呈现三次设计，在此基础上从设计意图、打磨思路、打磨细节进行具体的介绍，详细记录磨课的整个过程.

图2 磁屏蔽层有限元网格剖分图Fig.2 The finite element meshing of magnetic shielding

进行有限元求解,可得到在磁屏蔽边界条件下,单匝线圈产生的磁场分布,提取其中待求区域O、A、B点的磁场,可以得到磁屏蔽边界条件下随位置变化单匝线圈产生的磁场分布。

1.2 自由边界下线圈磁场求解

根据毕奥-萨法尔定律,电流元dl在与其相距r处产生的磁场为

(2)

其中,μ0=4π×10-7,I为线圈电流,当电流为圆线圈形式时,经积分求解,可得到单匝圆线圈电流在图1所示O、A、B点产生的垂直于其圆环面的磁场分别为:

(3)

其中,R为线圈半径,z为线圈中心与待求磁场区域中心距离,根据式(3)即可得到自由边界条件下单根导线位于不同位置时，在待求区域中心及边界点处产生的磁场大小。

1.3 线圈磁场等效增益系数模型建立

根据单匝线圈在磁屏蔽边界及自由边界下于待求磁场区域产生的磁场值,结合式(1),可得到O、A、B三点磁场等效增益系数。

(4)

由此,即可得到单匝线圈在不同位置产生的磁场等效增益系数模型。

2 磁屏蔽边界条件下线圈磁场模型建立及优化

根据单匝线圈在不同位置产生的磁场等效增益系数模型,结合自由边界下线圈磁场求解表达式,可将磁屏蔽边界下线圈磁场模型进行解析表达。设线圈总匝数为N,距离待求磁场区域中心位置距离分别为z1,z2,…,zN,则各匝线圈在待求磁场区域中O、A、B点分别产生的磁场总值可表示为:

(5)

定义待求区域磁场变化率为

(6)

为保证待求区域磁场中心O点至A及B点的磁场变化率均最小,建立以A、B点磁场变化率总值最小为目标的优化函数并设置约束条件:

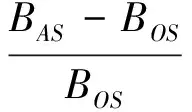
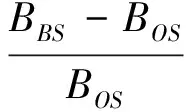
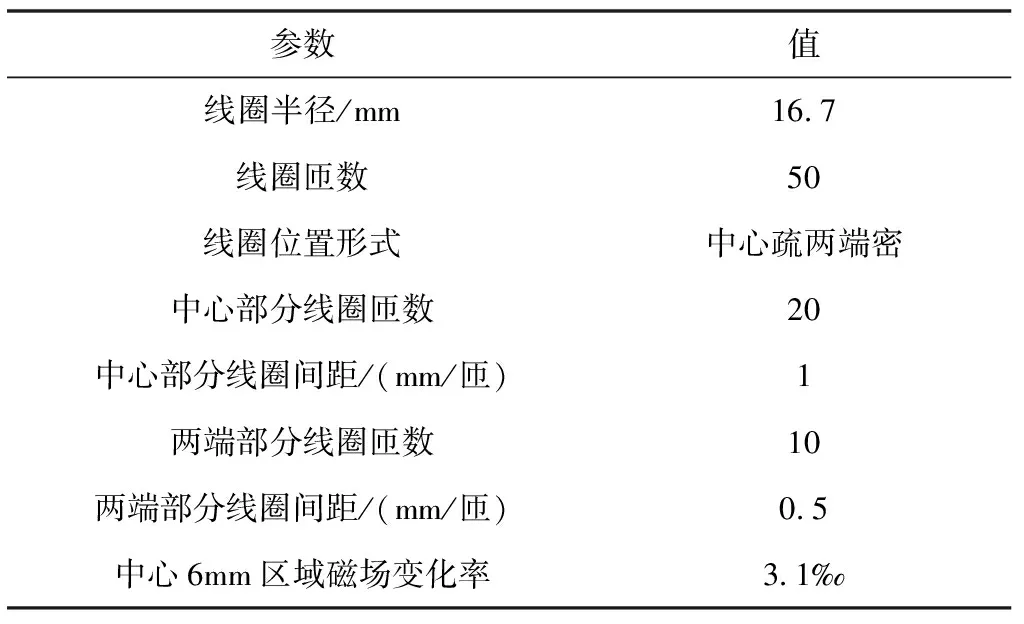
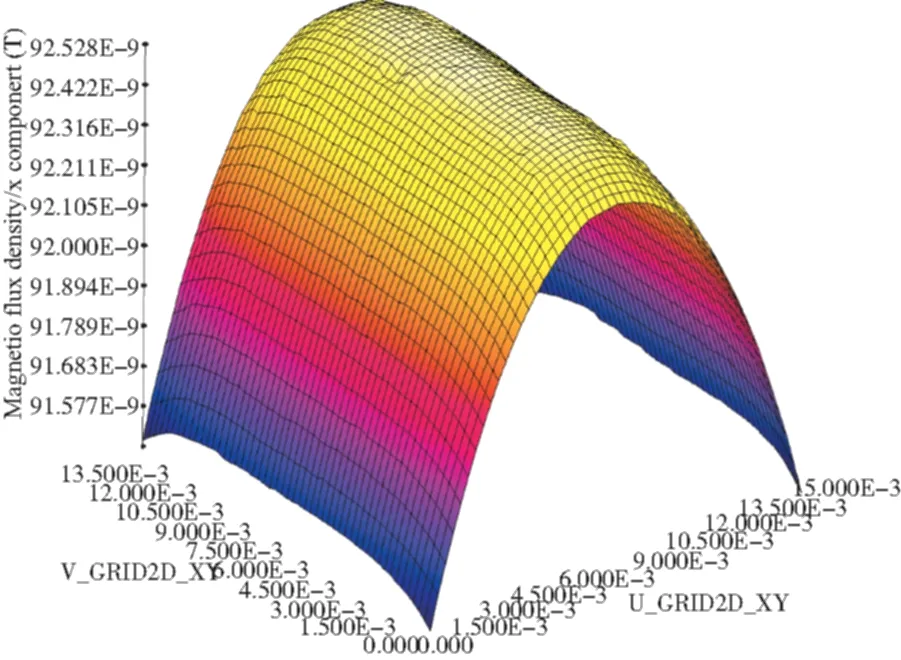
s.t. 0

其中,Rp为屏蔽桶内侧半径,hp为屏蔽桶内侧总高度,N为整数。对该含约束条件的非线性优化问题进行优化求解,可得到相应的线圈参数及磁场分布。

当磁屏蔽桶内径为18mm,高度为70mm,待求磁场区域为边长6mm立方体形状时,经优化得到其内部线圈参数如表1所示。

表1 磁屏蔽边界下高均匀磁场线圈优化结果

采用有限元方法对该优化结果进行校核,线圈内通入0.1mA电流,仿真得到待求磁场区域在XZ平面磁场分布如图3所示。

(a)磁场分布云图

(b)磁场分布曲面图图3 有限元仿真磁场分布图Fig.3 The magnetic field distribution of finite element simulation

可以看出,采用有限元方法得到待求区域的磁场变化率约3.9‰,与采用磁场等效增益系数解析方法得到的3.1‰相近似,表明了以磁场等效增益系数对磁屏蔽边界进行等效模拟的有效性。

3 试验测试及分析

根据上述优化结果,制作了磁场线圈及应用的磁屏蔽层,实物分别如图4、图5所示。

图4 高均匀磁场线圈实物图Fig.4 Photo of magnetic coil

图5 磁屏蔽层实物图Fig.5 Photo of magnetic shieldings

采用磁通门磁强计对所加工线圈磁场分布进行测量。完成线圈与磁屏蔽层的高精度装配后,给线圈施加1mA电流,将磁通门磁强计探头沿磁屏蔽层中心孔伸入,记录随探头在线圈中位置变化其测得的磁场值,探头位置-磁场关系曲线如图6所示。

图6 实测线圈内位置-磁场关系曲线Fig.6 Test curve of locations and magnetic flux densites of the magnetic coil

根据探头位置-磁场关系曲线,可以得到线圈磁场变化率实测结果,该结果与仿真结果对比如表2所示。

表2 磁场变化率试验测试及仿真结果对比

由表2可以看出,该线圈在待求区域产生的磁场变化率为4.5‰,相比采用等效增益系数法增大1.4‰。考虑到线圈在加工与装配过程中存在误差,从而破坏线圈磁场均匀性,因此表明了基于磁场等效增益系数进行磁场线圈设计方法的可行性。

4 结论

本文提出了线圈磁场等效增益系数,模拟磁屏蔽边界条件对线圈磁场作用,推导了磁场等效增益系数模型,并据此建立了磁屏蔽边界条件下高均匀磁场线圈模型,优化了线圈参数。通过对所设计线圈磁场均匀性进行测试,得到线圈所产生磁场变化率的实测值与仿真值分别为3.1‰和4.5‰,二者误差在允许范围内,表明该设计方法可以得到磁屏蔽边界条件下高均匀磁场线圈,可为微小型核磁共振陀螺中高均匀线圈设计提供有效手段。

[1] 秦杰, 汪世林, 高溥泽, 等. 核磁共振陀螺技术研究进展[J]. 导航定位与授时, 2014, 1(2): 64-69.

[2] Fang J., Qin J. Advances in atomic gyoscopes: a view from inertial navigation applications[J]. Sensors, 2012, 12(5): 6331-6346.

[3] 刘院省, 王巍, 王学锋. 微型核磁共振陀螺仪的关键技术及发展趋势[J]. 导航与控制, 2014, 13(4) :1-6.

[4] Meyer D, Larsen M. Nuclear magnetic resonance gyro for inertial navigation[J]. Gyroscopy and Navigation, 2014, 5(2): 75-82.

[5] Woodman K F, Franks P W, Richards M D. The nuclear magnetic resonance gyroscope: a review[J]. Journal of Navigation, 1987, 40(3): 366-384.

[6] Bulatowicz M D. Magnetic solenoid for generating a substantially uniform magnetic field: USA, U.S.Patent 8487729, B2[P]. 2013.

[7] 李攀, 刘元正, 王继良. 核磁共振陀螺多层磁屏蔽系统优化设计[J]. 中国惯性技术学报， 2016, 24(3):383-389.

[8] Odawara S, Muramatsu K, Komori S, et al. Method for evaluating shielding factor of double layered magnetically-shielded rooms for uniform magnetic field using exciting coils placed on one side[J]. IEEE Transactions on Magnetics, 2010, 46(6): 2357-2360.

[9] Zhang H, Geng J, Shen B, et al. Uniform magnetic field mapping with HTS coils:conceptual design and optimization[J]. IEEE Transactions on Optimization Applied Superconductivity, 2016， 26(3): 9000905.

[10] Öztürk Y， Aktas B. Generation of uniform magnetic field using a spheroidal helical coil structure[J].Journal of Physics: Conference Series, 2016, 667(1): 012009.

[11] Baranova V E, Baranov P F, Muravyov S V, et al. The production of a uniform magnetic field using a system of axial coils for calibrating magnetometers[J]. Measurement Techniques, 2015, 58(5): 550-555.

[12] Hadass T, Shuki W, Alexander F, et al. Mini-coil for magnetic stimulation in the behaving primate[J]. Journal of Neuroscience Methods, 2011, 194(2): 242-251.

[13] Cao Q, Han X, Zhang B, et al. Analysis and optimal design of magnetic navigation system using Helmholtz and Maxwell coils[J]. IEEE Transactions on Applied Superconductivity, 2012, 22(3): 4401504.

[14] Ales Z, Pavel R, Rainer K, et al. Precise scalar calibration of a tri-axial Braunbek coil system[J]. IEEE Transactions on Magnetics, 2015, 51(1): 1-4.

[15] Justin D, Julian V. Generation of long prolate volumes of uniform magnetic field in cylindrical saddle-shaped coils[J]. Measurement Science and Technology, 2014, 25(3):295-298.

Design Method of High Uniform Magnetic Coil for Nuclear Magnetic Resonance Gyroscope

WANG Chun-e, QIN Jie

(Beijing Institute of Automatic Control Equipment, Beijing 100074, China)

Nuclear Magnetic Resonance Gyroscope (NMRG) represents one of the developing trends of the next generation gyroscope with high precision and micro scale. With the decreasing in volume size of the NMRG, the sizes of internal magnetic shielding and the magnetic field coil also decrease, which not only requires high uniform magnetic field generated by small coil, but also requires the coil and the magnetic shielding layer adhered closely to reduce waste of space. Since the magnetic shielding boundary changes the flux path of the magnetic coil, the uniformity of the magnetic field decreases, which will constrain the control precision of the NMRG. To solve this problem, this paper proposes the concept of magnetic equivalent gain coefficient to simulate the influence of the magnetic shielding condition. Based on the concept, the optimization model is established and the coil parameters were optimized. Test of the uniformity of the designed magnetic coil shows that the design method is efficient and precise for gaining a high uniform magnetic coil under magnetic shielding condition, and can provide a significant design method reference for developing high performance NMRG in the near future.

NMRG; Magnetic coil; Magnetic shielding boundary; Magnetic uniformity

10.19306/j.cnki.2095-8110.2017.01.016

2016-11-17；

2016-12-26。

国家自然科学基金(61473268；61603052)

王春娥(1984-)，女，博士，工程师，主要从事核磁共振陀螺电磁技术研究。E-mail:wangchune2008@163.com

V241.5

A

2095-8110(2017)01-0089-05