连续冷原子束干涉陀螺仪研究进展

王安琪,孟至欣,李营营,薛洪波,冯焱颖

(1.精密测试技术及仪器国家重点实验室 清华大学精密仪器系,北京 100086； 2.空间天气学国家重点实验室, 国家空间科学中心 中国科学院,北京 100190)

连续冷原子束干涉陀螺仪研究进展

王安琪1,孟至欣1,李营营1,薛洪波2,冯焱颖1

(1.精密测试技术及仪器国家重点实验室 清华大学精密仪器系,北京 100086； 2.空间天气学国家重点实验室, 国家空间科学中心 中国科学院,北京 100190)

冷原子; 原子干涉;受激拉曼跃迁;陀螺仪

0 引言

自1991年被实验演示以来[1-2],光脉冲原子干涉仪(Light-Pulse Atom Interferometer, LPAIs)在很多领域显示了其作为极端灵敏传感器的潜力,例如重力测量[3-6]、惯性导航[7-10]、基础物理学[11]和基本常数测量[12-14]等等。

在原子干涉仪发展的早期阶段,原子干涉仪大量采用热原子束源作为物质波源,通过机械光栅[15-16]或者光学光栅[17-18]进行原子波包的相干操控。目前已经演示的最好性能指标的原子干涉陀螺是采用热原子束实现的,在短期噪声、长期稳定性和带宽(～ 110Hz)方面具有突出的性能指标[19-20]。热原子束干涉陀螺仪由于原子纵向速度较高(220～300m/s),在保证灵敏度不变的前提下进一步减小系统体积是该方案的一个技术难题。

使用冷原子作为物质波源是构建紧凑型原子干涉仪的自然解决方案,其中原子波源通常采用脉冲型发射的冷原子云团[10,20-22]。这种方案一般通过时间型的拉曼脉冲序列实现原子波包的相干操控。采用这种方案设计的原子干涉惯性传感器系统简单、操作灵活,便于集成,因此成为当前原子干涉惯性传感器研制的技术主流。由于原子云团的冷却、制备和相干操控需要一定的时间,尤其是原子云团的冷却和装载时间较长,一般在100ms量级,所以脉冲型冷原子干涉惯性系统一般周期时间长,因此导致数据率很低(干涉仪周期时间的倒数),限制了其在在动态环境下的应用。到目前为止,绝大多数报道的脉冲型冷原子干涉仪的工作数据率都在1Hz量级或者更低。脉冲型冷原子干涉方案数据率低的问题在研制面向惯性导航的原子干涉陀螺仪时更为突出,因为后者很少在静态环境下使用。针对这一问题,当前一般采用两种方法进行解决:一种方法是将常规惯性传感技术与原子干涉惯性技术进行融合,利用前者的高数据率和后者的高精度与长期稳定性实现高性能的惯性测量[23-25]。但这种方法要获得实际的应用以达到高精度惯性导航的要求,对于传统惯性传感器的性能和原子干涉惯性器件的性能的要求超过了当前实际技术水平。另一种方法即所谓的短作用时间的LPAIs或者高数据率LPAIs[26-28],这类方法在系统传感的灵敏度与系统尺寸之间做了折中,以牺牲系统灵敏度来换取数据率的提高。同时,也采用一些新的冷原子装载和再回收方式来有效缩短周期时间以达到提高数据率的目的。

本文描述了我们的原子干涉陀螺仪系统及初步的实验结果。我们采用87Rb冷原子束作为物质波源,利用空间分离的拉曼(Raman)脉冲进行原子波包的相干操控,实现了基于连续冷原子束源的Raman-Ramsey干涉和Raman-Mach-Zehnder干涉。

1 实验系统

冷原子束干涉陀螺仪实验装置如图1所示,图中只画出了一个原子束源的部分,实际系统是双向对射的原子束源,结构是对称的。真空系统是由3个真空腔体组成的三段式结构,其中中间真空腔体和两端的真空腔各共用一个离子泵,整个系统采用2台离子泵进行真空保持。中间腔体用于原子束的干涉,称为干涉腔,真空度为5×10-10Torr(铷源关闭的情况下)。两端的真空腔体用于形成双向对射的原子束,称为原子束源腔,真空度在铷源关闭的情况下达到2×10-9Torr。中间干涉腔与两端的原子束源腔体通过波纹管连接。原子束源腔体可以通过各自的三维精密调节机构进行原子束出射方向的精密调节,以保证2个对射的原子束路径一致。图2所示为陀螺仪在加磁屏蔽之前的物理系统照片。

图1 (a) 冷原子束干涉陀螺仪实验系统图; (b) 受激拉曼跃迁的能级图;(c)π/2-π-π/2 Raman脉冲序列产生方式Fig.1 (a) Schematic of the experimental layout for the atom interferometer based on a laser-cooled 87Rb atomic beam; (b) Level diagram for the ground states|1>and |2>and the excited state |e>;(c) Generation of the π/2-π-π/2 Raman pulse sequence

图2 原子干涉陀螺仪屏蔽之前的物理系统Fig.2 The experimental set-up of the atom interferometer gyroscope beforemagnetically shielding

连续冷原子束的产生采用典型的低速浓密源(Low-Velocity Intense Source,LVIS)方案[32-33]。冷原子被制备在一个标准的蒸气室三维磁光阱(3D-MOT)中。3D-MOT中心磁场的磁场梯度大约为15 G/cm,光路采用标准的回射光学构型。冷却光锁定到距87Rb 5S2S1/2,F=2→5p2P3/2,F′=3共振跃迁红失谐δ=4-5Γ(Γ=2π×6MHz,是87Rb的自然线宽)处。再泵浦光锁定到87Rb 5S2S1/2,F=1→5p2P3/2,F′=2共振跃迁处。冷却光和再泵浦光分别由2台外腔半导体激光器产生。冷却光激光器通过调制转移谱稳频到87Rb 5S2S1/2,F=2→5p2P3/2,F′=2共振跃迁频率,然后通过声光移频器移频到所需频率。再泵浦光激光器通过饱和吸收谱直接稳频到87Rb 5S2S1/2,F=1→5p2P3/2,F′=2共振跃迁频率。一路冷却光和再泵浦光通过锥形放大器进行功率放大,耦合到1根1分4的单模保偏光纤中,每2路分别用于双向对射的2个原子束源的横向冷却光。横向冷却光通过自制的光纤准直器将输出光准直成一个25mm×100mm的矩形光斑射入原子束源腔的对应窗口,然后被对面的一个镀有λ/4薄膜的反射镜反射回来形成对射的横向冷却光。另一路冷却光直接通过1根1分2的单模保偏光纤输出用于2个原子束源的推射光。冷却光的光强大约为4.5mW/cm2。推射光通过一个光纤准直器准直成直径为φ30mm的光斑进入对应的推射光窗口。推射光通过一个置于干涉腔和原子束源之间的λ/4波片+反射镜组进行反射形成对射的光路。该λ/4波片和反射镜在镜片中心通过超声钻孔形成φ1mm的通孔。该通孔导致推射光方向形成光压的不平衡,使冷却的原子连续从通孔泄漏出去形成原子束。

原子束的横向准直性受通孔大小和横向冷却光作用区域的影响较大。原子束的纵向速度、温度和原子通量决定于冷却光的功率、失谐量和磁场性能的影响。原子束的纵向最可几速度可以通过调节这些参数在10～20m/s之间,原子束的通量最大可以到4×109atoms/s(距离出射位置0.8m处)。

在原子束从3D-MOT中形成并出射到干涉腔后,冷原子首先被态制备光制备到超精细基态磁不灵敏子能级F=1,mF=0态。态制备光为锁定到F=2→F′=2共振跃迁频率的圆偏振光(σ跃迁)和F=1→F′=0共振跃迁频率的线偏振光(偏振方向垂直于磁场方向,也为σ跃迁)。然后冷原子就直接用于干涉，不再做进一步态制备和准直。通过偏置磁场选择处于|F=1,mF=0>的磁不敏感塞曼子级上的原子用于干涉,大约 1/4原子用于后续干涉。

双光子速度选择的受激拉曼跃迁(Stimulated Raman Transition)被用来相干操控原子波包。拉曼光路如图1所示。主激光器是一个780nm的外腔半导体激光器(DL Pro, Toptica, 德国),通过光纤电光调制器移谱和频率调制谱锁定到距87Rb原子的F=1→F′=1共振跃迁频率红失谐Δ=2π×1.07GHz处。然后主激光器的光分为2路。一路通过声光移频器移频60MHz后注入锁定到一个从激光器(Slave laser 1)中进行放大,记该光的工作频率为ω1;另一路主激光器的光通过一个光纤电光调制器(Fiber Electro-Optical Modulator,FEOM, EOspace,美国)调制后,注入锁定到另一个从激光器(Slave laser 2)中进行选频放大,输出光工作频率记为ω2。光纤电光调制器的驱动射频频率设定为ω00-2π×60MHz=2π×6.775GHz,其中ω00=ω1-ω2=2π×6.835GHz对应87Rb原子的基态超精细能级跃迁频率。第二路从激光器的输出通过频率选择的侧边带注入锁定技术，锁定到光纤电光调制器输出的-1级边带上[34]。60MHz声光调制器和6.775GHz的射频信号都参考到同一个铯原子钟上。其中,6.775GHz的射频信号采用自制的基于非线性传输线的射频驱动源。2路从激光器输出光混合后通过一个快光电探测器进行拍频测量,拍频信号的-3dB线宽在60MHz声光调制器工作时大约为1.5Hz,而当声光调制器不工作时其-3dB线宽小于1Hz(实验室频谱分析仪的分辨率极限)。由此可见,声光调制器驱动信号引入的相位噪声导致线宽变差。2路从激光器的输出光分别利用1台半导体锥形放大器(BoosTA,Toptica, 德国)进行功率放大到大约600mW,然后偏振相互垂直耦合进同一路单模保偏光纤,并利用一个自制的光纤准直器形成直径为φ60mm的高斯光束输出。如图1(c)所示,该高斯光束通过光阑阻挡形成宽度d=1.0mm和间距L=9.5mm的3个片光,中间片光用于形成π脉冲的拉曼激光,两侧的片光用于形成π/2脉冲的拉曼激光,其W中中间片光的光强是两侧片光光强的1倍。通过仔细调节光纤准直器输出光的准直,使得2个π/2拉曼脉冲与π拉曼脉冲平行。然后,3个拉曼脉冲通过一个λ/4波片(QWP2)将其中2个相互垂直的线偏振光分量转化为2个相反旋向的圆偏振光。该拉曼光束通过原子束后,通过另一个λ/4波片(QWP3)重新变为相互垂直的线偏振光,然后通过偏振分光棱镜将其中的ω1和ω2进行空间分离,抛弃掉ω2而只允许ω1分量反射回原子束。这样就形成了双向对射构型的拉曼激光作用,产生了σ+-σ+或者σ--σ-形式的多普勒敏感的拉曼跃迁。3个拉曼激光束安装在同一个光学平板上,可以相对原子束进行转动。去掉λ/4波片QWP2和阻挡回射光可以实现多普勒不敏感的拉曼跃迁。

冷原子束干涉条纹通过扫描π脉冲拉曼光的相位来获得。如图1(a)所示,我们在π脉冲拉曼光ω1分量处放置一个光学相位板。该相位板厚度为9.53mm,相对π脉冲拉曼光成45°角,采用类似外腔半导体激光器光栅扫描的方式通过一个压电陶瓷进行转动扫描。当压电陶瓷驱动相位板转动时,π脉冲拉曼光ω1分量的光程发生变化,因此导致拉曼光ω1和ω2的相对相位发生变化,引起原子干涉相移的改变。

原子干涉信号通过荧光法检测处于F=2态的原子通量来获得。检测光被锁定到F=2→F′=3循环跃迁频率上,利用自制的光纤准直器与狭缝光阑形成片光,与通过3个拉曼脉冲之后的原子束作用。诱导的荧光通过一个φ50mm的透镜收集,利用1个光电倍增管(PMT,H7422-50, Hamamatsu, 日本)进行检测。

如图1所示,干涉区与拉曼光方向平行的均匀偏置磁场通过集成在干涉真空腔中的四极导线柱形成[35]。4A的电流可以产生强度为0.96Gauss的偏置磁场,对应塞曼频移为0.67MHz。考虑实验中多普勒敏感的拉曼跃迁线宽(大约为500kHz),该磁场足以将处于不同塞曼子能级的原子分离,使得我们可以只选择布居在F=1,mF=0态的原子用于干涉。

2 实验结果与讨论

冷原子束的速度和通量通过飞行时间法(the time of flight,TOF)进行测量。利用一个阻断光对原子束进行开关,同时记录处于F=2态的原子的荧光信号的下降沿,可以解算出冷原子束的相关信息。图3(a)所示为从TOF信号中获得的原子速度谱。通过改变冷却光的偏振和磁场梯度,原子束的纵向最可几速度可以调节到vz0=15.0m/s 、纵向速度分布为δvz=3.5m/s(FWHM)。

(a)

(b)图3 冷原子束的典型测量结果(a)利用飞行时间法(TOF)测量的冷原子束的纵向速度分布;(b)π脉冲的拉曼跃迁谱显示冷原子束的态制备效果Fig.3 Measurement of the cold atomic beam (a) The longitudinal velocity distribution of the cold atomic beam measured using the time of flght method (TOF)； (b) The state preparation of |F=1, mF=0>, which is indicated by the Raman transition spectra driven by a π Raman pulse

采用速度敏感的拉曼跃迁谱来测量原子在不同基态超精细mF子能级上的布居。如图3(b)所示,在我们的实验中,一共观测到7个拉曼跃迁峰,这是由环境磁场和地磁场影响而导致作用区净磁场矢量方向与拉曼光矢量方向不平行,从而使得态制备同时存在π跃迁和σ跃迁。这会使得态制备效率的定量测量变得困难。图3(b)中,标记为0的拉曼跃迁峰对应磁不敏感的mF=0→mF=0拉曼跃迁;标记为±1的拉曼跃迁峰对应磁敏感的mF=±1→mF=0的拉曼跃迁;类似地,±2分别对应磁敏感的mF=+1→mF=+1和mF=-1→mF=-1的拉曼跃迁;±3对应磁敏感的mF=+1→mF=+2和mF=-1→mF=-2的拉曼跃迁。从图3中蓝色点线可以看出,如果只有F=2→F′=2态制备光作用,原子会被以不对称形式布居到所有的基态超精细磁子能级。图3(b)中黑色实验曲线显示,当同时施加F=2→F′=2和F=1→F′=0态制备光时,相对其他磁子能级,更多原子被布居到了F=1,mF=0的磁不敏感子能级。F=1→F′=0态制备光的偏振方向对于制备效率的影响明显,当存在π跃迁时,态制备效率会严重下降,如图3(b)中红色点线的实验曲线所示。态制备效率可以通过各个拉曼跃迁峰的相对强度进行粗略估计。

连续冷原子束通过空间分离的拉曼光束操控,3个拉曼脉冲宽度相同,均为d=1.0mm,对应拉曼脉冲作用时间τ=d/vz0也为常值。拉曼跃迁的拉比频率(Rabi frequency)Ωeg通过改变拉曼光强来调节,使3个拉曼脉冲的拉比相位φ=Ωegτ可以设置到π或π/2。图4所示为对应的3个拉曼脉冲的多普勒敏感构型的mF=0→mF=0拉曼跃迁。2个π/2拉曼脉冲的跃迁峰值幅度相等,都为π拉曼脉冲跃迁峰值幅度的一半。将拉曼激光束的方向稍微偏离与原子束方向相垂直的方向,多普勒敏感的拉曼跃迁峰的位置会与残余的多普勒不敏感的拉曼跃迁峰的位置偏移。这种残余的多普勒不敏感的拉曼跃迁是因为拉曼光的偏振不纯引起的。需要通过设置拉曼光相对频差ω1-ω2来补偿上述多普勒频移和反冲频移。从π拉曼脉冲(τ=67μs)驱动的速度敏感拉曼跃迁谱估计,拉曼跃迁线宽～336kHz对应原子束的横向速度分布为±6.5cm/s(FWHM)。

图4 分别由π/2、π和π/2拉曼脉冲驱动的多普勒敏感的拉曼跃迁Fig.4 Doppler-sensitive Raman transition spectra driven by theπ/2-π-π/2 Raman pulse sequence

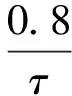
π/2-π-π/2拉曼脉冲序列的原子干涉信号可以描述为

(1)

其中,Φa为加速度诱导的干涉相移;ΦΩ为转动引起的Sagnac相移;φ1、φ2和φ3分别为第1个π/2脉冲、第2个π脉冲和第3个π/2脉冲拉曼激光的初始相位。我们通过转动相位板扫描π脉冲拉曼激光的相位来获得干涉条纹。图5所示的干涉条纹反映了干涉相移的输出是π脉冲拉曼激光相移的2倍。压电陶瓷最大位移为9μm,通过计算π脉冲拉曼光相移与相位板转动角度的关系,可求得对应原子干涉相移约为30rad。这种相位调制技术可以用于补偿和调制干涉相位。

图5 π/2-π-π/2拉曼脉冲序列的Mach-Zehnder原子干涉条纹Fig.5 The π/2-π-π/2 Mach-Zehnder atom interference fringe as a function of the optical phase of the π Raman pulse

干涉条纹的对比度受多个影响因素限制。首先,原子束的纵向速度分布是决定干涉信号对比度的主要因素。拉曼激光的拉比相位,φ=Ωegτ,需要相对原子束的最可几速度vz0,优化以得到π和π/2脉冲。图6所示为采用多普勒不敏感的π/2-π/2拉曼激光构型获得的Ramsey干涉条纹。分离共振场的长度为2L=19mm。2个π/2脉冲质检的原子相干作用时间为T=1.3ms,对应的中心条纹线宽为δRamsey=1/(2T)=390Hz。在速度平均效应之下[10],可以分辨出高于4阶干涉条纹,n=vz0/δvz=～4。这说明采用冷原子束代替热原子束(n=～1)[19]进行干涉,由于前者窄的纵向速度分部,原子干涉仪的可观测条纹数目会增多,导致传感器灵敏度的提高。

图6 π/2-π/2拉曼脉冲形成的Ramsey干涉条纹Fig.6 Raman-Ramsey fringes driven by π/2-π/2 Raman pulses

其次,原子束的横向速度分布会进一步降低干涉条纹对比度。当采用多普勒敏感的拉曼脉冲(对射拉曼激光构型)进行干涉操控时,横向速度范围在Δvx=δ12/keff内被选择与拉曼脉冲作用。在我们的实验中,拉曼跃迁的线宽为12kHz,横向选择速度范围大约为Δvx=5mm/s。这意味着原子束横向速度分布(±6.5cm/s)范围内只有很少一部分原子参与了干涉。横向选择速度范围外的原子不能有效被拉曼脉冲操控,使得干涉对比度和信噪比大大恶化。在当前的实验中,图4中的条纹峰-峰值对应大约107个原子参与干涉,条纹对比度大约为17%。

第三,由于冷原子束的横向速度分布,原子束会在飞行过程中由于热膨胀而逐渐发散。这使得其与拉曼脉冲相互作用时,由于拉曼光束的空间不均匀,不同原子感受到的拉比频率不同,原子干涉会因为这种不均匀平均效应而被破坏。原子束的进一步的亚多普勒横向冷却可以一定程度上改善这种影响。

另一种影响因素是拉曼激光的相对ac Stark频移,原理上这可以通过仔细调节2个拉曼光(ω1和ω2)的功率比I2/I1来消除。但是由于功率抖动引入的附加相位噪声会导致干涉条纹对比度的降低,严重时甚至会导致干涉信号消失(当非零相对ac Stark频移大于拉曼跃迁线宽时)。实验中,功率比I2/I1最终被设定到0.6附近,靠近零相对ac Stark频移的理论值(对于87Rb原子和失谐量Δ=2π×1.07GHz)[36]。

原子干涉信号的噪声水平当前主要受限于检测光和拉曼光散射造成的背景噪声。干涉信号的波动主要来自于原子束通量波动和拉曼脉冲的功率和相位抖动。这部分噪声需要进一步抑制。

3 结论与展望

与脉冲冷原子干涉陀螺仪相比,连续冷原子束干涉陀螺可以通过频率或者相位调制技术[37-38]进行陀螺仪的噪声补偿或闭环控制,这是连续冷原子束源方案的一个重要优势。脉冲型冷原子束源方案由于过低的数据率使得相应的调制技术效果不佳。

在本文撰写阶段,我们已经完成了更大面积Sagnac干涉、双向对射原子束干涉、干涉信号的相位调制与初步闭环控制,目前数据正在深入分析和整理中,实验结果将会在后续文章中详细报道。

[1] Riehle F, Kisters T, Witte A, et al. Optical Ramsey spectroscopy in a rotating frame: Sagnac effect in a matter-wave interferometer[J]. Physical Review Letters, 1991, 67(2): 177.

[2] Kasevich M, Chu S. Atomic interferometry using stimulated Raman transitions[J]. Physical Review Letters, 1991, 67(2): 181.

[3] Peters A, Chung K Y, Chu S. High-precision gravity measurements using atominterferometry[J]. Metrologia, 2001, 38(1): 25.

[4] Yu N,Kohel J M, Kellogg J R, et al. Development of an atom-interferometer gravity gradiometer for gravity measurement from space[J]. Applied Physics B, 2006, 84(4): 647-652.

[5] Bodart Q, Merlet S, Malossi N, et al. A cold atom pyramidal gravimeter with a single laser beam[J]. Applied Physics Letters, 2010, 96(13): 134101.

[6] Hu Z K, Sun B L, Duan X C, et al. Demonstration of an ultrahigh-sensitivity atom-interferometry absolute gravimeter[J]. Physical Review A, 2013, 88(4): 043610.

[7] Canuel B, Leduc F, Holleville D, et al. Six-axis inertial sensor using cold-atom interferometry[J]. Physical Review Letters, 2006, 97(1): 010402.

[8] Durfee D S, Shaham Y K, Kasevich M A. Long-term stability of an area-reversible atom-interferometer sagnac gyroscope[J]. Physical Review Letters, 2006, 97(24): 240801.

[9] Wu S, Su E, Prentiss M. Demonstration of an area-enclosing guided-atom interferometer for rotation sensing[J]. PhysicalReview Letters, 2007, 99(17): 173201.

[10] Dickerson S M, Hogan J M,Sugarbaker A, et al. Multiaxis inertial sensing with long-time point source atom interferometry[J]. Physical Review Letters, 2013, 111(8): 083001.

[11] Müller H, Peters A, Chu S. A precision measurement of the gravitational redshift by the interference of matter waves[J]. Nature, 2010, 463(7283): 926-929.

[12] Fixler J B, Foster G T, McGuirk J M, et al. Atom interferometer measurement of the Newtonian constant of gravity[J]. Science, 2007, 315(5808): 74-77.

[13] Cadoret M, De Mirandes E, Cladé P, et al. Combination of Bloch oscillations with a Ramsey-Bordé interferometer: new determination of the fine structure constant[J]. Physical Review Letters, 2008, 101(23): 230801.

[14] Rosi G, Sorrentino F, Cacciapuoti L, et al. Precision measurement of the Newtonian gravitational constant using cold atoms[J]. Nature, 2014, 510(7506):518-521.

[15] Keith D W,Ekstrom C R, Turchette Q A, et al. An interferometer for atoms[J]. Physical Review Letters, 1991, 66(21): 2693.

[16] Lenef A, Hammond T D, Smith E T, et al. Rotation sensing with an atom interferometer[J]. Physical Review Letters, 1997, 78(5): 760.

[17] Rasel E M, Oberthaler M K, Batelaan H, et al. Atom wave interferometry with diffraction gratings of light[J]. Physical Review Letters, 1995, 75(14): 2633.

[18] Tonyushkin A, Kumarakrishnan A, Turlapov A, et al. Magnetic coherence gratings in a high-flux atomic beam[J]. The European Physical Journal D, 2010, 58(1): 39-46.

[19] Gustavson T L, Landragin A, Kasevich M A. Rotation sensing with a dual atom-interferometer Sagnac gyroscope[J]. Classical and Quantum Gravity, 2000, 17(12): 2385.

[20] Ping W, Run-Bing L I,Hui Y, et al. Demonstration of a Sagnac-type cold atom interferometer with stimulated Raman transitions[J]. Chinese Physics Letters, 2007, 24(1): 27.

[21] Gauguet A, Canuel B, Lévèque T, et al. Characterization and limits of a cold atom Sagnac interferometer[J]. Physical Review A, 2009, 80(6):70.

[22] Tackmann G, Berg P, Schubert C, et al. Self-alignment of a compact large-area atomic Sagnac interferometer[J]. New Journal of Physics, 2012, 14(1): 015002.

[23] Merlet S, Le Gou⊇t J, Bodart Q, et al. Operating an atom interferometer beyond its linear range[J]. Metrologia, 2009, 46(1): 87.

[24] Geiger R,Ménoret V, Stern G, et al. Detecting inertial effects with airborne matter-wave interferometry[J]. Nature Communications, 2011, 2(1):474.

[25] Canciani A. Integration of Cold Atom Interferometry INS with Other Sensors[C]. Proceedings of the International Technical Meeting of the Institute of Navigation, 2012:151-185.

[26] Butts D L,Kinast J M, Timmons B P, et al. Light pulse atom interferometry at short interrogation times[J]. Journal of the Optical Society of America B, 2011, 28(3):416-421.

[27] McGuinness H J, Rakholia A V, Biedermann G W. High data-rate atom interferometer for measuring acceleration[J]. Applied Physics Letters, 2011, 100(1):011106.

[28] Rakholia A V, McGuinness H J, Biedermann G W. Dual-axis high-data-rate atom interferometer via cold ensemble exchange[J]. Physical Review Applied, 2014, 2(5): 054012.

[29] J Guéna J, Dudle G, Plimmer M D, et al. Experimental demonstration of intermodulation effects in a continuous cesium fountain microwave frequency standard[C]//2007 IEEE International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum. IEEE, 2007: 477-482.

[30] Devenoges L, Stefanov A, Joyet A, et al. Improvement of the frequency stability below the dick limit with a continuous atomic fountain clock[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2012, 59(2): 211-216.

[31] DiDomenico G, Devenoges L, Joyet A, et al. Uncertainty evaluation of the continuous cesium fountain frequency standard FOCS-2[C]//2011 Joint Conference of the IEEE International Frequency Control and the European Frequency and Time Forum (FCS) Proceedings. IEEE, 2011: 1-5.

[32] Lu Z T, Corwin K L,Renn M J, et al. Low-velocity intense source of atoms from a magneto-optical trap[J]. Physical review letters, 1996, 77(16): 3331.

[33] Wang X J,Feng Y Y, Xue H B, et al. A cold 87Rb atomic beam[J]. Chinese Physics B, 2011, 20(12): 126701.

[34] Xue H B, Feng Y Y, Wang X J, et al. Note: Generation of Raman laser beams based on a sideband injection-locking technique using a fiber electro-optical modulator[J]. Review of Scientific Instruments, 2013, 84(4): 046104.

[35] Morris D. Shielded four‐conductor magnetic field assembly[J]. Review of Scientific Instruments, 1984, 55(9): 1483-1485.

[36] Schmidt M. A mobile high-precision gravimeter based on atominterferometry[D]. Humboldt-Universität zu Berlin, Mathematisch-Naturwissenschaftliche Fakultät I, 2011.

[37] Gustavson T L. Precision rotation sensing using atom interferometry[D]. Stanford University, 2000.

[38] 朱常兴, 冯焱颖, 叶雄英,等. 利用原子干涉仪的相位调制进行绝对转动测量[J]. 物理学报, 2008, 57(2):808-815.

Research Progress in a Continuous Cold Atomic Beam Interferometer Gyroscope

WANG An-qi1, MENG Zhi-xin1, LI Ying-ying1, XUE Hong-bo2, FENG Yan-ying1

(1.The State Key Laboratory of Precision Measurement Technology and Instruments, Tsinghua University, Beijing 100084, China; 2.The State Key Laboratory of Space Weather, Center for Space Science and Applied Research, Chinese Academy of Sciences, Beijing 100190, China)

Cold atoms；Atom Interferometry；Stimulated Raman Transition；Gyroscope

10.19306/j.cnki.2095-8110.2017.01.014

2016-11-01；

2016-12-06。

国家自然科学基金 (61473166)

冯焱颖(1977-)，男，副教授，主要从事原子光学、精密惯性测量技术、微电子机械系统(MEMS)方面的研究。E-mail: venifeng@gmail.com

V249.32+3

A

2095-8110(2017)01-0077-08