不同电离层模型对北斗共视的精度影响分析

陆 华, 孙 广, 肖 云, 郭美军, 翟 伟, 熊 超

(1. 航天恒星科技有限公司(503所),北京 100086; 2. 西安航天天绘数据技术有限公司, 西安 710054; 3. 西安测绘研究所, 西安 710054)

不同电离层模型对北斗共视的精度影响分析

陆 华1, 孙 广2, 肖 云3, 郭美军2, 翟 伟2, 熊 超2

(1. 航天恒星科技有限公司(503所),北京 100086; 2. 西安航天天绘数据技术有限公司, 西安 710054; 3. 西安测绘研究所, 西安 710054)

GNSS共视时间传递已成为远程高精度时间同步的主要技术手段之一,我国自主研制的北斗导航系统已经服务于亚太地区,基于北斗共视进行高精度时间传递已成为我国时频领域的研究热点。为了提高导航系统定位精度,需降低或消除导航定位过程中的各类误差,其中电离层为影响北斗共视的主要误差。研究了常用的几种电离层修正算法,利用2014年7月份的观测数据分析不同电离层模型对北斗共视钟差的精度影响,给出了残差标准差和稳定度值。分析结果表明:经各种电离层修正后,钟差精度都有所提高,其中双频电离层修正最优,比VTEC格网模型和Klobuchar模型分别提高22%和30%。对于不同星座,GEO卫星计算的钟差修正后精度明显优于MEO、IGSO卫星。

北斗共视;Klobuchar;双频;电离层

0 引言

北斗卫星导航系统是我国自主研发的卫星导航系统,目前已服务亚太区域,开展北斗时间传递研究及应用将成为我国时频领域发展的重要趋势[1]。

电离层时延是影响北斗共视时间精度的主要因素之一[2-4]。北斗信号通过电离层时,信号路径会发生弯曲,传播速度也会发生变化。因此,用北斗共视进行远距离时间比对时,必须考虑电离层时延的问题。

目前,在高精度远程时间传递中,电离层时延的计算方法主要有Klobuchar模型、VTEC格网模型以及双频改正模型[5-7]。本文分别应用三种电离层时延的计算方法生成北斗共视钟差数据,分析了不同电离层模型对共视钟差的影响精度以及钟差的稳定度。

1 电离层模型

1.1 Klobuchar模型

单频常用的电离层改正模型为Klobuchar模型。如式(1),该模型中的垂直延迟在白天与地方时t的余弦函数近似,夜间则近似为一常数[8]。

(1)

1.2 双频改正模型

双频改正模型利用双频数据的组合来消除电离层影响。对频率为f1、f2的电磁波进行观测,其电离层折射影响如式(2)

(2)

由式(2)得式(3)

(3)

用ρ0表示无电离层影响时,电磁波从卫星到测站的距离;ρ1、ρ2表示频率为f1、f2的电磁波经电离层从卫星到测站的距离。则

(4)

式(4)相减,并结合式(3)可得式(5)

(5)

从式(5)中可得对应频率上电离层延迟量。

利用双频模式可消除电离层影响的95%。但是在太阳辐射最为强烈的正午,会存在明显的残差,所以应避开这个观测时间段。双频修正电离层延迟能够消除大部分电离层延迟误差,但也降低了对于广播星历的依赖性,并引入组合伪距测量噪声量。

1.3VTEC格网模型

IGS公布了电离层信息的数据交换格式IONEX,提供时段长度为2h、经差为5°和纬差为2.5°的VTEC格网图。

为了得到纬度为β、经度为λ的某地点在时刻t的总电子含量TEC,首先对历元时刻的TEC含量进行四站网格空间内插[9],如图1所示。

图1 四站网格空间内插原理Fig.1 Principle of spatial interpolation method

按实际的时间对历元之间做内插,具体操作步骤为:

采用四点网格内插法计算出Ti和Ti+1两个时刻的总电子含量,计算如式(6)

(6)

得到空间内插后进行相应时间点的时间双线性内插,具体计算如式(7)

(7)

计算时刻t的电离层时延,取得穿刺点对应时刻垂直方向上的TEC后,选取映射函数,就能获得导航信号在传播路径上的倾斜TEC值,如式(8)

(8)

其中,C为光速,f为信号载波频率,Z为中心电离层高度的天顶距。

2 北斗共视时间传递

2.1 原理

北斗共视原理与GPS、GLONASS共视原理相同,如图2所示。

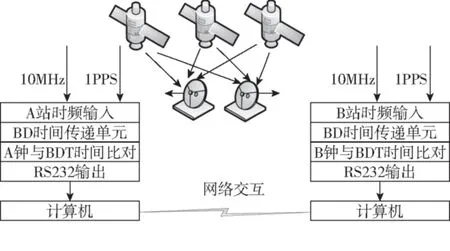
图2 北斗共视原理Fig.2 The principle of BDS common-view

A、B两站在同一时间观测同一北斗卫星,北斗接收机输出秒脉冲代表北斗时间,将该秒脉冲作为计数器的关门信号,本地原子钟输出的秒脉冲作为计数器的开门信号,分别在A、B两地可得到本地时tA、tB与北斗卫星时tBD之差,两者做差后可获得两地时间差[10]。

通过北斗共视法进行时间传递可完全消除星载钟误差,消除部分对流层、电离层的附加时延误差和卫星位置误差[11]。实际A、B两站获得钟差结果如式(9)

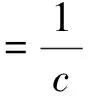
[τSA(TA)-τSB(TB)]

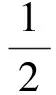
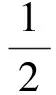
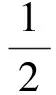
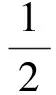
(9)

2.2 共视数据处理

北斗共视数据处理流程如图3所示,具体处理步骤如下[11-12]。

图3 北斗共视数据处理流程Fig.3 The data process flow of BDS common-view

首先读取北斗原始伪距数据,进行粗差剔除;读取同频点、同支路以及同类型的伪距数据;对两站坐标进行修正;然后根据伪距时间点获取最近的广播星历值,并计算该点的卫星位置;添加各类误差修正;最后将卫星钟差结果做中位数法剔除粗差,再用最小二乘法拟合为每0.5h一个点,可获得两站钟差序列。

3 实验结果分析

本文计算了Klobuchar模型、格网模型、双频修正以及未用任何电离层模型的钟差，分析了钟差结果的统计参数及频率稳定度。频率稳定度反映了时差的随机误差,值越小表示越稳定。残差标准差表示钟差结果的稳定性,均方根误差表示准确性。

3.1 电离层时延结果

利用2014年7月的观测数据分析了修正电离层后计算的钟差与未修正电离层计算的钟差的差值,即不同的电离层修正模型对共视钟差的时延修正量。

图4 Klobuchar电离层模型修正的时延Fig.4 Time delay of Klobuchar ionospheric corrections

图5 格网电离层模型修正的时延Fig.5 Time delay of grid ionospheric corrections

图6 双频电离层改正的时延Fig.6 Time delay of dual frequency ionospheric corrections

从图4～图6中可以看出，电离层时延是具有日周期变化的,因为电离层电子总含量与太阳活动及日地关系密切。从图6中可以看出，双频修正的时延大约在-10～20ns变化,图5中格网模型修正的时延大约在-10～15ns变化,而图4中Klobuchar模型修正的试验大约在-10～10ns变化,说明格网模型和双频修正的电离层比Klobuchar模型的效果好。

3.2 精确度分析结果

通过北斗共视算法,对北斗GEO1号卫星进行分析,分别用Klobuchar模型、格网模型、双频修正以及不用电离层修正模型计算获得了两站钟差,将钟差通过最小二乘拟合,最后对残差结果进行分析。

从图7与图8中可以看出,三种电离层时延修正方法获得的共视钟差比未修正电离层获得的钟差精度都有所提升,从表1可以看出双频修正后共视钟差精度最优,为2.296ns；格网模型修正后的精度次之,为2.441ns；Klobuchar模型修正后的钟差精度为3.117ns；双频修正后的钟差精度比格网模型和Klobuchar模型修正后的钟差精度分别提升了22%和30%。

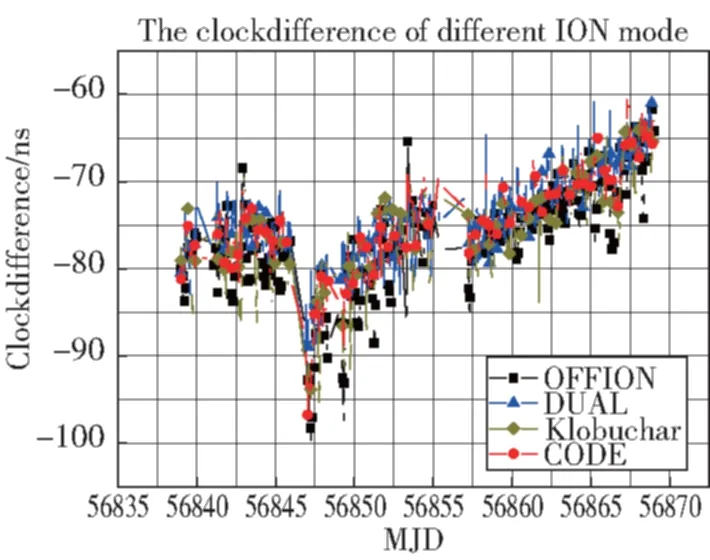
图7 不同电离层模型计算的共视钟差波形图Fig.7 The clock difference of different ionospheric models

图8 基于GEO1号卫星最小二乘拟合后钟差波形图Fig.8 The clock difference of different ionospheric models by using least squares based on GEO1 satellite

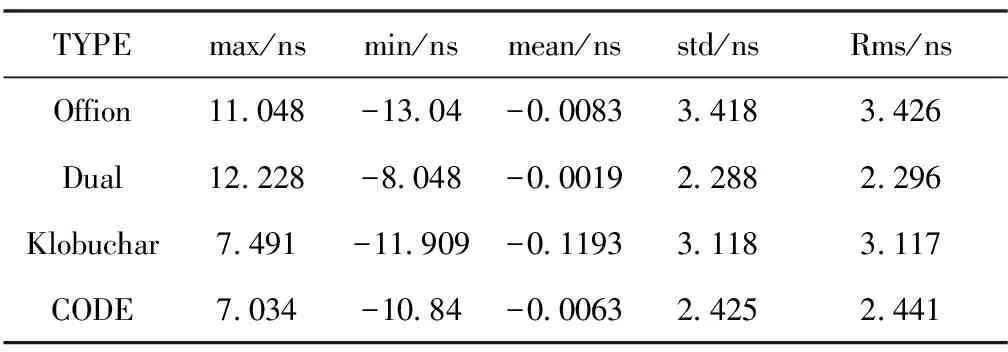
TYPEmax/nsmin/nsmean/nsstd/nsRms/nsOffion11048-1304-0008334183426Dual12228-8048-0001922882296Klobuchar7491-11909-0119331183117CODE7034-1084-0006324252441

3.3 稳定度分析结果

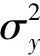
(10)

式中,xi是第i个测量结果,时间间隔为τ0,N是钟差个数,τ是计算Allan方差的采样间隔,τ=nτ0。

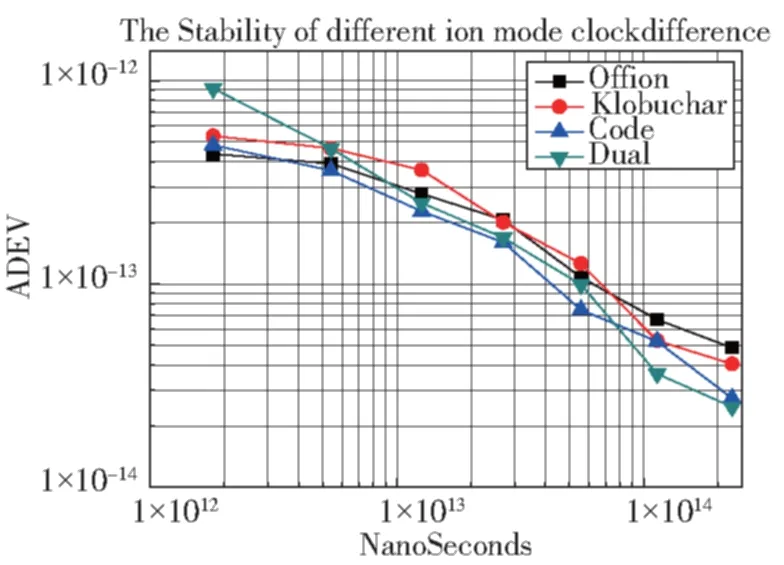
图9 不同电离层模型计算的钟差稳定度图Fig.9 The stability of clock difference by using different ionospheric models

图10 不同电离层模型计算的全部钟差点稳定度图Fig.10 The stability of total points clock difference by using different ionospheric models

从图9、图10可以看出,在短期时间内,修正电离层后的钟差稳定度没有得到改善,Klobuchar计算的共视钟差在短时间内的稳定度甚至比未修正电离层时延的共视钟差稳定度还差。随着时间的变长,不同电离层修正后计算的钟差稳定度明显优于未校正电离层时延的共视钟差。从表2中看出,在228600s稳定度,双频修正后最好,为2.48×10-14,其次是格网电离层模型,为2.74×10-14,最后是Klobuchar模型,为4.03×10-14。

表2 不同电离层模型钟差稳定度值

3.4 基于不同星座分析结果

对不同星座的钟差修正结果进行比较,分别对IGSO6和MEO11卫星展开分析。

从图11中可以看出,基于IGSO卫星电离层修正后的共视钟差精度提升的幅度不明显,从表3中也反映出修正后与未修正的钟差结果相差不大。从图12中可以看出，MEO卫星计算的共视钟差效果一般。从表4中可以看出,Klobuchar模型计算精度还变差,这主要因为基于IGSO卫星和MEO卫星观测共视数据量较少。而格网模型修正后的共视钟差精度比双频还好,这主要因为在IGS站分布密集的区域,格网模型修正后的钟差精度就会变好。

图11 基于IGSO6号卫星最小二乘拟合后钟差波形Fig.11 The clock difference of different ionospheric models by using least squares based on IGSO6 satellite

TYPEMax/nsMin/nsMean/nsStd/nsRms/nsOffion8237-14820007427927598Dual6395-11510003827126881Klobuchar6168-13040014533533201CODE6872-1320001227427089

图12 基于MEO11号卫星最小二乘拟合后钟差波形Fig.12 The clock difference of different ionospheric models by using least squares about MEO6 satellite

TYPEMax/nsMin/nsMean/nsStd/nsRms/nsOffion7989-12462-00223113123Dual7819-12193-00213183217Klobuchar6268-13231-00333743733CODE4262-10985-00252682678

对不同星座不同电离层的钟差统计如表5所示,同一种电离层模型修正后,基于GEO卫星计算的钟差精度明显比其他两种卫星计算的钟差精度高,基于MEO卫星计算的钟差精度最差。总体而言,用双频修正电离层计算的钟差精度最优。

表5 基于不同星座不同电离层计算的钟差残差指标值

4 结论

本文选择2014年7月份的共视数据,分别应用Klobuchar电离层模型、CODE格网电离层模型、双频电离层修正模型计算了两个站的共视钟差,分析了共视钟差的残差标准差、均方根以及稳定度指标。分析结果表明:应用不同的电离层模型修正后的共视钟差精度有明显的提升,利用双频修正电离层比格网模型修正和Klobuchar电离层模型修正后的共视钟差精度分别提升了22%和30%。对于不同星座,GEO卫星计算的钟差修正后精度明显优于MEO、IGSO卫星。本文的研究结果对北斗共视进行电离层模型选择方面可提供参考。

致谢 感谢国际GNSS监测评估系统(iGMAS)的监测评估中心(MAC)为本文提供数据支持。

[1] 刘大杰, 陶本藻.实用测量数据处理方法[M].北京:测绘出版社, 2000:79-81.

[2] 杨元喜.北斗卫星导航系统的进展, 贡献与挑战[J].测绘学报, 2010, 39(1):1-6.

[3] 李征航, 赵晓峰, 蔡昌盛.利用双频GPS观测值建立电离层延迟模型[J].测绘信息与工程, 2003, 28(1):41-44.

[4] 袁运斌.基于GPS的电离层监测及延迟改正理论与方法的研究[D].武汉:中国科学院测量与地球物理研究所, 2002.

[5] 武文俊, 李志刚, 杨旭海.电离层延迟改正模型的研究[C]//第二届中国卫星导航学术年会, 2011.

[6] 张小红, 李征航, 蔡昌盛.用双频GPS观测值建立小区域电离层延迟模型研究[J].武汉大学学报(信息科学版), 2001, 26(2):140-143, 159.

[7] 王先毅, 孙越强, 杜起飞， 等.一种实时双频电离层修正方法[J].科学技术与工程, 2012, 12(5):992-995.

[8] 余明, 郭际明, 过静珺.GPS电离层延迟Klobuchar模型与双频数据解算值的比较与分析[J].测绘通报, 2004(6):5-8.

[9] 李志刚, 程宗颐, 冯初刚， 等.电离层预报模型研究[J].地球物理学报, 2007, 50(2):327-337.

[10] 阳仁贵, 欧吉坤, 闻德保.GPS 广播星历误差及对定位结果的影响[J].测绘信息与工程, 2006, 31(1):1-3.

[11] 广伟.GPS PPP时间传递技术研究[D].北京:中国科学院研究生院， 2012.

[12] Guo M J, Lu H, Xiao Y， et al. Analysis of BeiDou signals on the accuracy of common-view time transfer[C]// China Satellite Navigation Conference (CSNC) 2015 Proceedings, Volume I. Springer Berlin Heidelberg, 2015: 425-436.

[13] 高小珣, 高源, 张越, 等.GPS 共视法远距离时间频率传递技术研究[J].计量学报, 2008, 29(1):80-83.

Analysis of Different Ionospheric Model on the Accuracy of BDS Common-View

LU Hua1, SUN Guang2, XIAO Yun3, GUO Mei-jun2, ZHAI Wei2, XIONG Chao2

(1. Space Star Technology Co.,Ltd., Beijing 100086, China; 2. Xi’an Aerors Data Technology Co.，Ltd., Xi’an 710054, China； 3. Xi’an Research Institute of Surveying and Mapping, Xi’an 710054, China)

GNSS common-view time transfer technology has become one of the main means of remote high-precision time synchronization, China has independently developed the BDS which has been used in the Asia-Pacific region, the high-precision time transfer based on BDS common-view has become the research hot spot of time-frequency fields. In order to improve the positioning accuracy of the navigation system, it is needed to reduce or eliminate the errors of navigation and positioning process, and the ionospheric errors are the main errors on BDS common-view. Several ionospheric correction algorithms are studied, and the data observed in July 2014 are used to analyze the influences of different ionospheric models on the accuracy of the clock difference of BDS common-view, and the standard deviation and stability of value of residual are also presented. The results show that: the accuracy of the clock difference has been improved when conducting various ionospheric corrections, of which dual frequency ionospheric correction has the optimal performance, the accuracy of the clock difference increased by 22% and 30% respectively compared with VTEC grid model and Klobuchar model. And the difference of corrected clock calculated by the GEO satellites has higher precision than those calculated by MEO, IGSO satellite.

BDS common-view; Klobuchar; Dual frequency; Ionosphere

10.19306/j.cnki.2095-8110.2017.01.010

2016-06-27；

2016-08-01。

地理信息工程国家重点实验室开放研究基金资助项目(SKLGIE2015-M-1-4)

陆华(1979-)，男，高级工程师，主要从事GNSS卫星导航方面的研究。E-mail:nngu_cast@163.com

U666.12

A

2095-8110(2017)01-0053-07