解题教学应立足于解决过程,着眼于培养品质
汪轩亭
摘 要:数学教育的最高目标、长远目标和最终目标是数学精神品质的培养。这个目标是我们数学教学者应该追求的价值所在。数学教学中的一个重要组成部分是解题教学,在教学中我们要培养学生的理性精神、独立思考精神和求真精神;在解题教学过程中要注重活动经验,进而培养数学严谨品质;在解题教学过程中要强调自我反思,进而培养自省品质。
关键词:解题教学;培养品质;解决过程;严谨品质;自省品质
解题教学是数学教学的重要组成部分,尽管新课改实施了多年,不可回避的事实是,我们的数学教学仍然有向数学考试教学异化的危险,不少学生在数学学习中爱模仿、怕思考,缺乏理性精神和独立思考精神;浅尝辄止、敷衍了事……可见,以培养学生数学精神品质为教学目标和教学价值趋向的思考和实践还显得比较缺失。良好的数学品质包括实事求是、不断求真的数学态度;落笔有据、言之有理的严谨品质;独立思考、勇于创新的精神以及对自己的数学能力充满自信等内涵。
一、立足于解决过程应引导“存疑质疑”,着眼于培养“严谨品质”
案例1:已知二次函数y=a(x2-6x+8)(a>0)的图像与x轴分别交于点A、B,与y轴交于点C,点D是抛物线的顶点。
(1)如图1,连接AC,将△OAC沿直线AC翻折,若点O的对应点O'恰好落在该抛物线的对称轴上,求实数a的值;
(2)如图2,在正方形EFGH中,点E、F的坐标分别是(4,4)、(4,3),边HG位于边EF的右侧,小林同学经过探索后发现了一个正确的命题:“若点P是边HG或边EH上的任意一点,则四条线段PA、PB、PC、PD不能与任何一个平行四边形对应相等(即这四条线段不能构成平行四边形)。”若点P是边EF或边FG上的任意一点,刚才的结论是否也成立?请你积极探索,并写出探索过程。
(3)这是苏州市中考最后一个压轴题(题略),在学生练习后,我们与部分学生进行了交流,发现部分基础非常好的学生对第二问看不懂或理解不全,因为此问题与平时做的数学题目在表达方式上有很大的不同。我们认为,之所以会产生这样的问题,与平时教学中始终由教师提出问题,存疑生疑时由教师进行解释有很大的关系,学生在平时解决问题的过程中缺少存疑、生疑、质疑的习惯,当然就不能对本题的问题形式有严谨的分析和思考。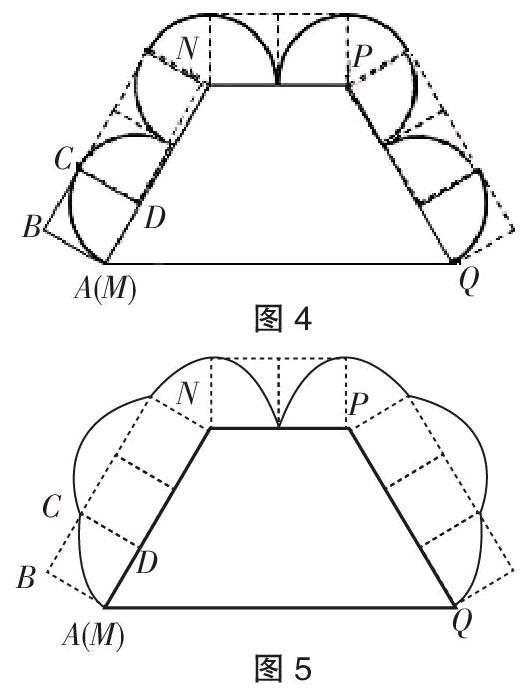
当学生在解题的过程中出现问题时,常见如下两种处理方式:一种是为了所谓的课堂目标和效率,教师替代学生,指出问题所在;另一种是为了让学生真正认识问题与本质,通过问题串,逐步引领学生从问题中走出来。本题的解答过程中学生存疑、质疑的地方是“四条线段PA、PB、PC、PD不能与任何一个平行四边形对应相等”是什么意思?因为教材只讲对应角、对应线段等对应相等。题目中的解释是:“这四条线段不能构成平行四边形。”那么什么样的四条边不能构成平行四边形呢?为了回答这个问题,可以从这个问题的反面来考虑,什么样的四条边能构成平行四边形?两组对边分别相等的线段可以构成平行四边形等。那么,不能构成平行四边形的四条边又满足什么条件呢?可能是四条边都不相等;可能是两条边相等,其余不相等……那现在的情形是怎样的呢?我们发现,当解题者从生疑出发,一步步进行质疑的时候,就在逐步接近问题的解决,就在使自己的思维活动变得严谨。所以,在平时的解题教学中,我们要坚持进行解题分析,特别是解题过程中让学生学会自己生出疑问、处理疑问,应该是帮助学生体会思维方法力量、优化思维品质的有效途径,培养学生质疑等严谨的品质。
二、立足于解决过程应强调“自我反思”,着眼于培养“自省品质”
案例2:已知如图3,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°。正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合。现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动。
(1)请在所给的图3中,用尺规画出点A在正方形整个翻滚过程中所经过的路线图。
(2)求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S。
这是江苏省无锡市中考的一个中档题,考后我们对此题也进行了访谈,学生认为此题虽然新颖,但难度不是太大,但从阅卷中我们发现,还有相当多的学生是错误的。既然学生认为不难,但得分率为什么并不高?通过阅卷分析我们认为,学生出错的根源在于解题过程中缺少自我反思意识,本质上是缺少自省品质。
大量教学实践研究表明,在数学解题教学和学生学习过程中,如果在获得正确答案后不对学习过程进行回顾和反思,那么解题活动就有可能停留在经验水平上,事倍功半;如果在每一次解题以后都能对自己的思路作自我评价,探讨成功的经验或失败的教训,那么学生的思维就会在更高的层次上进行再概括,并促使学生的思维进入理性认识阶段,从而使数学学习事半功倍。立足于解决过程,应该在解题过程中把反思纳入其中作为必不可少的一个环节,强调反思过程就是要对解题的全过程进行自觉、深入、反复的思考,再看一看、想一想逻辑上有无漏洞;解题方法是否正确;有无其他方法;有无捷径;结论能否推广;能否变化条件得出新的命题;等等。本题的解决过程中涉及正方形作的翻滚运动,它显然不是平移和翻折,应该是旋转运动,既然是旋转,就涉及旋转中心和旋转角度,此处由于要考虑点A在正方形整个翻滚过程中所经过的路线,因此,本质上要考虑的是每次旋转的圆心和半径的问题,错误者翻滚结果如图4,而正确的翻滚结果如图5。如果在错解的基础上再进行反思环节,就可以看出点A旋转到点C处时,点C已到AN边上,第一次旋转运动结束,接下去是又一次新的旋转,从而很快就找到错误。由此可见,反思的作用正是体现在查漏、补缺、纠错、归纳、总结、提升。所以,在平时的解题教学中,立足解决过程要强调自我反思,通过已学的知识去学习新的知识,通过分析做过的习题去领悟解题经验,通过解题经验去处理新的问题,通过出错纠错的经验去改进解题,最后去领略数学解题的无限风光,而这正是一个学生通过自我反思,养成自省品质的完美过程。
总之,数学教学应该以数学知识为载体,在解决问题的过程中提炼数学知识中包含的思想、观点和方法,逐步培养学生的数学思想方法、数学精神品质,并运用这些真正的数学学习收获去分析、探索、研究、解决今后学习、工作和生活中遇到的问题。
(作者單位:江苏省苏州市吴江实验初级中学)

