基于差分进化和RBF响应面的混合优化算法1)

邓凯文 陈海昕

(清华大学航天航空学院，北京100084)

基于差分进化和RBF响应面的混合优化算法1)

邓凯文 陈海昕2)

(清华大学航天航空学院，北京100084)

针对气动优化等昂贵优化问题，提出了一种基于差分进化和RBF响应面的混合优化算法HSADE，该方法结合了差分进化算法的强全局寻优能力和RBF响应面方法的快速局部搜索能力，能够同时有效地提高算法的局部搜索效率和全局寻优能力.对各子算法中的策略和逻辑进行了多项改进，提出和应用了基于双败淘汰赛的竞赛赛制和参数自适应等改进策略.对HSADE使用多个典型算例进行了测试，并横向对比了NSGA-II，MOPSO和多目标差分进化算法.测试结果表明，在大多数问题中HSADE在以世代距离表征的局部搜索效率和以超体积比表征的全局寻优能力两项指标上都优于其他算法，证实了以上混合策略及算法改进的有效性.将该算法应用于一个翼型优化问题和一个二维超声速喷管膨胀面优化问题，并横向对比未经改良的差分进化算法DE和另一种混合算法NARSGA，结果表明在接近1000次的函数评估下，HSADE能相对其他算法进一步对翼型减阻0.5 count，在喷管优化中HSADE得到的结果也好于其他两种算法，表明该方法具有较强工程应用价值.

差分进化,响应面方法,计算流体力学,多目标优化,优化设计

引言

随着高性能计算技术的快速发展，高精度数值模拟在飞机气动设计中已得到大量应用.尽管基于高精度数值模拟的优化设计已被广泛应用且取得了较好的效果[1-3]，但其进一步应用仍受到较大的限制.尤其是面对“昂贵优化问题”[4]，即目标函数评估的计算耗费很大的时候.以飞行器气动优化为例，三维客机翼身组合体全模的雷诺平均方程(RANS)计算，需使用6000万网格.利用64个核心的计算节点进行计算，一个工况耗时通常可达36h.在存在时限的工程设计中，以上复杂度的问题的总计算次数往往是严格受限的，这就要求优化方法能够在限制总函数评估次数下具有更好的优化效果.

因此针对类似于气动优化的“昂贵优化问题”，优化算法应有较高的优化效率.局部搜索效率和全局寻优能力是评价优化算法效率最重要的两大指标.通常而言，启发式算法的局部优化效率要大大低于梯度类算法，但具有更好的全局寻优能力.为提高启发类算法的效率，一种做法是与其他优化方法组合得到“混合算法”，以提升其综合性能.

近年来研究人员在混合优化算法上开展了大量的改进和尝试.提出了包括以启发式算法结合基于梯度方法构建的混合算法[5-6]、以代理模型方法为主[7-8]的混合算法、以及启发式算法和代理模型方法组合的混合算法[9-11]等混合方法.在气动优化设计领域，研究者对遗传算法[12-14]、代理模型方法[15-16[17-18]开展了大量测试和应用.在此基础上，混合算法也因其较好的综合性能得到了该领域学者的关注，文献[19]提出了一种基于粒子群算法和Kriging响应面的应用于气动优化问题的混合算法，文献[20]提出了一种将文化基因算法(memetic algorithm)作为局部搜索算子以提升遗传算法搜索效率的混合算法并应用于气动优化，文献[21]提出了一种基于NSGA-II[22]和Kriging响应面的混合优化算法用于多段翼型等昂贵问题的优化.

目前广为应用的启发式算法多具有精英保留机制[23]，即算法会保留精英个体而逐代淘汰较劣个体，典型的例子有SPEA2[24]，NSGA-II[22]等.因此在拥有精英保留机制的混合算法中，若引入辅助方法加强局部的深度搜索，其得到的个体往往趋近局部最优因而性能指标优秀，它们在接下来的数代中会引导种群进化直至被后代超越；若引入辅助方法进行增强的广度搜索，其最终得到的个体虽存在较好的多样性，但由于性能指标通常不佳而难以存活多代，在降低算法效率的同时并不能很好地维持种群的多样性.基于优势互补的原则，一种理想的混合算法组合是一种具有强全局寻优能力的主算法结合帮助其进行快速局部搜索的辅助方法.

差分进化 (di ff erential evolution,DE)是一种于1995年提出的启发式算法[25]，闻名于其强鲁棒性和对高维问题良好的适应性，拥有很强的全局寻优能力.径向基函数(radial basis function,RBF)响应面(response surface,RS)方法是一种使用径向基函数进行插值的代理模型方法，也是现在人工神经网络最著名的模型之一[26]，在工程优化中被广为使用.这种方法相较于工程中常用的其他代理模型如Kriging响应面，薄板样条曲面等有着光顺性好，数学描述简单的特点，同时它的精度也比较高[27].

本文根据以上思路，提出了一种针对气动优化等昂贵优化问题的基于差分进化和RBF响应面的自适应混合算法HSADE(hybrid self-adaptive di ff erential evolution)，通过在鲁棒性较好的差分进化算法的主流程中嵌入高精度的RBF响应面方法，利用代理模型拟合已计算数据，给出最佳个体预测，加入差分进化算法的种群，以提高算法整体的数据利用率；从而通过较小的响应面计算量换来较大的搜索效率提升. HSADE以差分进化为主体，因此也是以代为单位进行迭代优化的.

值得注意的是，在优化过程中，响应面插值并不取代CFD计算，它的功能是为主算法在设计变量空间内搜索新的具有潜在最优性能的待分析个体.因此整个优化过程的仍基于高精度的CFD分析.而RBF响应面会随优化进程中新的计算结果实时更新以提升最优点预测能力.

此外，本文在提出两种方法的混合策略同时也对它们各自进行了一些改进，以提高算法整体效能.

1 混合算法HSADE

1.1 算法整体结构

HSADE的核心思想是利用多种优化策略给出的蕴含不同特性的个体，确保种群多样性，强化精英个体，以同时提高算法的局部和全局寻优能力.

具体而言，HSADE的思路是以差分进化为主干，在每一代的进化结束阶段向种群中依次嵌入由RBF响应面给出的提升算法搜索效率的个体和由空间增量填充法(increment space filling ISF)给出的提升种群多样性的个体，和原有差分进化的种群中通过择优机制保留的高度多样的个体共同构成子代个体进入下一代，以提升算法的整体效率.同时考虑到为提高种群目标函数评估的计算效率，每代各个体的函数评估将同时并行执行.

HSADE的优化流程概括在图1中，描述如下：

(1)初始化算法参数，置代数k=1，使用中心采样方法和空间增量填充法为主的为实验设计方法(design of experiments,DOE)产生初代种群Pk作为设计起点，并为待构建响应面提供一个分布均匀的样本集；其中空间增量填充法旨在按顺序找到一系列个体，其设计变量x∗满足如下特性

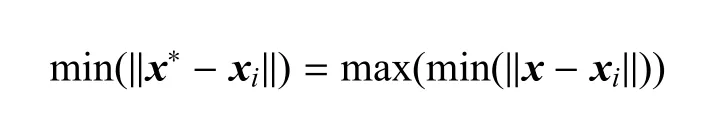
其中xi代表当前种群中各个体的设计变量；

(2)将种群Pk按照差分进化的流程依次进行变异和交叉，产生试验种群Uk；使用RBF响应面拟合所有已计算点的数据，使用差分进化算法优化响应面参数以最小化拟合误差，使用差分进化算法在响应面上寻优，得到潜在最优个体集合Ok；利用空间增量填充法给出增加种群多样性的个体集合Dk；

(3)并行评估Uk,Ok和Dk中各个体目标函数；

(4)对Pk和Uk按照双败淘汰制执行选择操作并淘汰末位个体，得到获胜种群Pk′；

(5)令Pk+1=Pk′∪Ok∪Dk，若未满足结束条件，令k=k+1，重新回到步骤(2).

优化流程中种群大小设为Np，总优化代数为Ngene，其余各主要参数都经自适应改造以提高算法通用性.

1.2 子算法介绍

1.2.1 差分进化

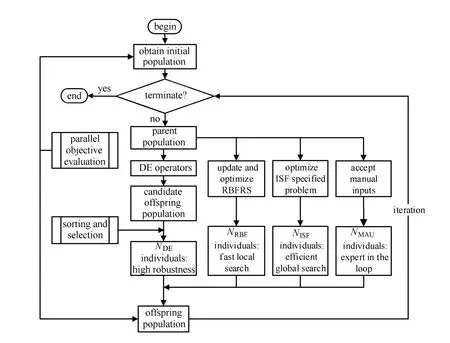
图1 HSADE优化流程图Fig.1 Optimization fl w chart of HSADE

差分进化算法是一种将实数编码应用于连续空间优化的启发式算法，和遗传算法相似，它主要有三个过程：变异、交叉和选择.为避免混淆，将优化问题中一个设计变量和其对应的目标函数组合起来统称为一个个体个体上标表示代数，下标表示其在种群中的位置.当代的种群记作目标函数对设计变量的映射记为按以上定义，差分进化的过程可被简单归纳为以下步骤：

(1)读取参数，置代数k=1，初始化种群Pk；

(2)令Pk为父代种群，对Pk中的每一个个体执行(3)～(5)步；

(3)从当前种群中挑选n个基矢量，n取决于变异方式

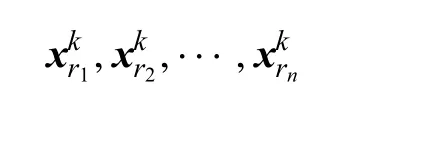
(6)令k=k+1，若满足结束条件，输出最终种群相关信息，否则回到步骤(2).

以上步骤(2)～(5)的具体形式均有多种变体，因此差分进化算法并不局限于单一的形式，它可以用统一的记号描述：DE/X/Y/Z[25].X表示变异过程中对基矢量的选择方式，主要有/rand/，/best/和/targetto-best/三种；Y表示参与变异的矢量对数；Z表示交叉方式，详细介绍见文献[25].HSADE选用/target-tobest/1作为差分进化算的变异方式，选用二项式交叉作为其交叉方式.

1.2.2 径向基函数响应面

径向基函数响应面是一种基于径向基函数的插值方法，假设已获得一系列已知的采样点，(xi,yi)(i=1,2,···,NS),dim(xi)=Nx,dim(yi)=Ny.对于一个待评估点(x,y)，在已知x的情况下由下式给出y的估计值

其中，λ为大小为NS×Ny的权重系数矩阵，φ(x)为大小为1×NS的行向量，它们分别按下式确定

φ(x)的元素为

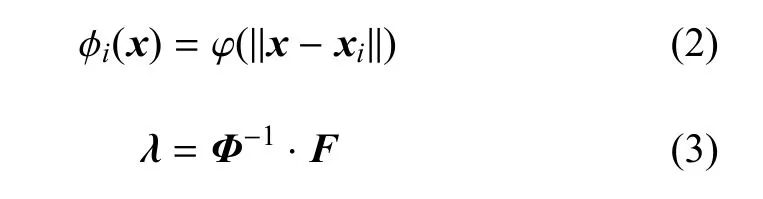
Φ的元素为

F的元素为

式中，Φ和F分别为基函数矩阵和目标函数矩阵，ϕ为径向基函数，其较为常用的类型被总结在表1中. HSADE采用的基函数为逆多项式函数(inverse multiquadric).

表1 径向基函数类型Table 1 Di ff erent types of radial basis functions

2 子算法的改进

在引入基本算法形成混合算法的同时，本文也对基本算法分别提出了一些改进措施，以提升算法效率.

2.1 对于差分进化的改进

2.1.1 基于双败淘汰制的选择算子

为进一步提高算法的整体效率，HSADE采用一种称为双败淘汰赛的选择算子，设每代的选择过程在父代种群和以父代种群生成的试验种群间进行，且父代种群中各个体已按非占优排序方法[22]和最近邻域距离进行了从最优到最劣的排序，令Uk中的个体与Pk一一对应，则选择流程如下：

(1)在父代种群中抽取前Nb个个体，Nb为预定义的正整数满足Nb＜Np，则子代种群的前Nb个个体由经基于种群环境的择优准则在2.1.2节详述)竞争得出；若负于则将加入败者组B，设B的最终大小为NB；

(3)将混合组C由非占优排序方法和最近邻域距离进行排序，选出最好的Np-Nb个个体，并将其保留，作为子代种群的后个个体

2.1.2 种群信息辅助的择优逻辑

在传统差分进化中，择优在父代和子代种群的个体间一一进行，这种策略存在可能淘汰潜在的较优个体的弊病.一种典型的情况是，当使用差分进化算法求解一个双目标最小化优化问题，假设此时种群内正在进行个体A={xA,yA}和个体B={xB,yB}的竞争以选出胜者进入子代，个体A,B和当代种群的Pareto前缘如图2所示.

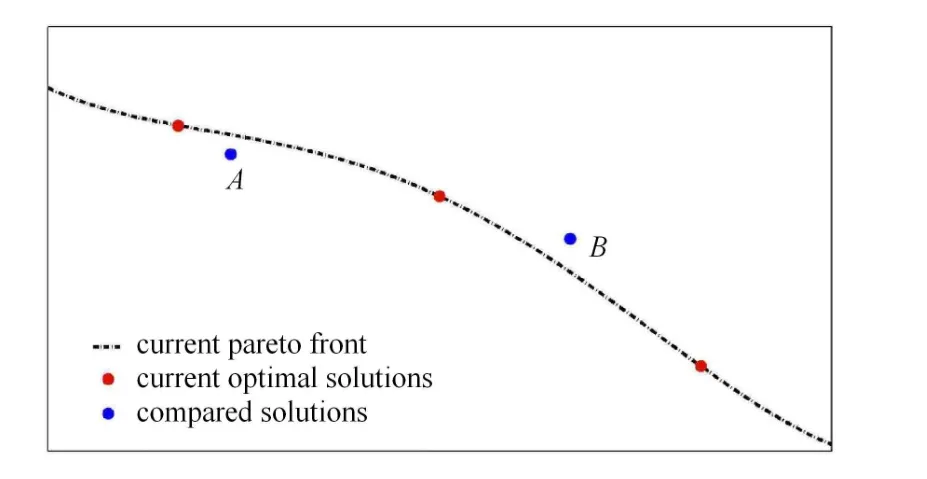
图2 一种典型的择优情景Fig.2 A typical selection occasion

在这种情况中，因为个体A和B是Pareto互不占优的，且个体B的拥挤程度优于A(A距离上游点更近)，因此传统的择优逻辑会倾向于保留B而淘汰A.但实际上个体A才是真正利于种群整体进化的，因为它位于当前Pareto前缘下方，能将其向前推进.这是传统差分进化中择优逻辑存在的漏洞，它忽略了竞争过程中种群环境的信息.在择优过程中这种逻辑对个体的优劣判断仅以其竞争对手作为唯一参照，这会导致潜在的判断失准.对于这个问题，本文采用一种如图3描述的择优逻辑，称为种群信息辅助的择优逻辑，在择优过程中种群内各个体信息会被引入择优决策过程以挑选出最利于种群进化的个体进入子代.

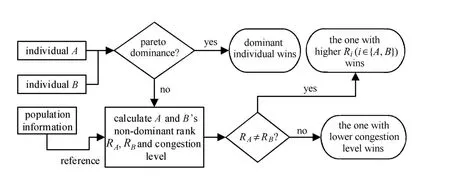
图3 种群信息辅助的择优逻辑Fig.3 Population information enhanced selection logic

2.1.3 参数自适应策略

在基本差分进化算法中，算法性能严重依赖于参数的选择[28-29]. 为增强算法对问题的适应性, HSADE中应用了一种简洁的参数自适应策略，具体方法为：在算法开始阶段，遍历种群中所有个体，为其分配一个独立的变异常数Fi和交叉概率因子CRi，其中i为个体编号.若在指定代数Nc内位于种群相同位置的个体在种群中的排名没有上升，则按下式更新其算法参数

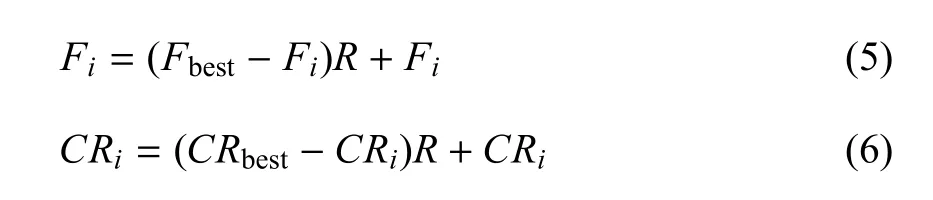
其中，下标best表示在指定代数Nc内Pareto占优等级上升最多的个体的参数，R为[0,1]内的随机数，以上参数自适应逻辑是一个促使各个体参数逐渐向更适宜进化的参数靠近的过程.

2.2 对于径向基函数响应面的改进

2.2.1 响应面参数优化、误差的度量与快速估计

在优化进行的每一代中，HSADE会对响应面的参数进行优化以最小化插值误差.由于RBF响应面为完全插值，且在昂贵气动优化问题中测试点是稀缺的，本文采用文献[30]的交叉验证方法定义响应面误差以充分利用已计算数据，避免响应面过拟合.具体而言，按式(7)定义误差矩阵E

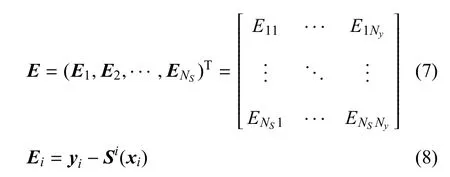
式中Si(xi)为响应面在样本集合中去掉第i个个体时,在设计变量为xi时给出的估计值.

如此定义的误差矩阵E可按下式快速计算

式中λij为权重矩阵的分量，X=Φ-1，其余定义见式(2)～式(4).令nj为第j个目标函数的归一化因子，定义响应面拟合误差eRS为

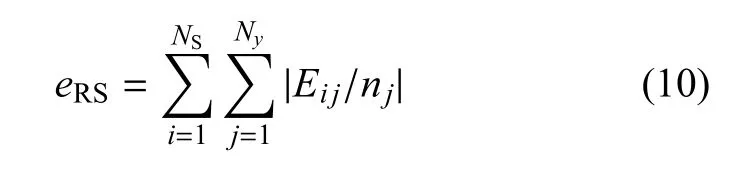
2.2.2 RBF响应面参数重分配策略

本文提出了一种对RBF响应面参数进行重分配的策略.如上小节描述，经典径向基函数响应面理论中，多目标插值可以表示为

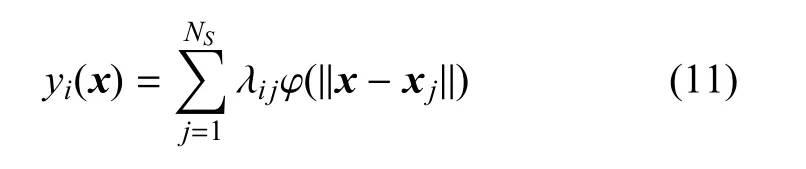
式中，每个目标函数在插值时对应每个采样点的基函数ϕ都是相同的，为一个统一预定义的径向基函数.由于采样点在设计变量空间的分布存在疏密不同的区域，物理直观上，这些区域中的采样点对应的基函数应该具有差异化的函数参数以体现采样点在空间的分布.

本文通过重分配响应面方法中对应于各样本点的径向基函数参数，以适应不同区域样本点的疏密度，达到提升插值精度的目的.以逆多项式函数为例，具体操作如下：

(1)对编号为i的采样点，取ri为设计变量空间中其他采样点与该采样点的最小欧氏距离，用于描述其稀疏程度；

(2)定义一列差异化的径向基函数

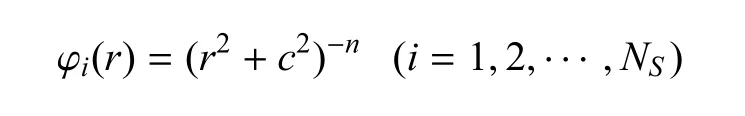
其中ci=kSri，kS为全局缩放因子，原径向基函数响应面的待优化参数c被kS取代；

(3)重新定义插值公式和径向基函数矩阵

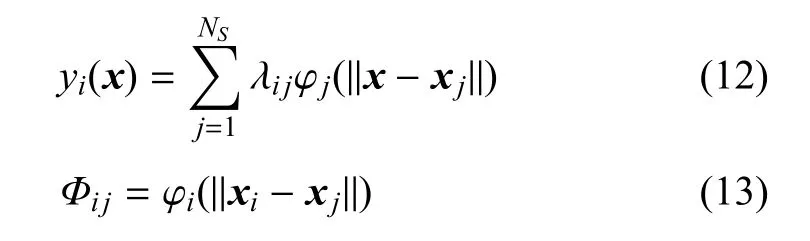
(4)根据重新定义的径向基函数矩阵由式(3)求新的权重矩阵.

响应面参数经重分配后，对应每个采样点的基函数参数都不相同，具体效果见于下节的测试部分.

3 算法测试

本节将使用一些典型测试函数验证和评估RBF响应面的拟合精度和HSADE的综合优化效能.

3.1 响应面拟合精度验证

本节将基本RBF响应面，经过2.2.2节参数重分配后的RBF响应面(简写为SRBF)和Kriging响应面在一些典型测试函数[31]上的拟合精度进行对比，对于每个测试函数，分别取NS=20,40,80,120个随机采样点，NT=1600个固定测试点.每种情况独立运行80次.使用平均归一化均方根误差作为3种方法拟合误差的评价指标，定义为

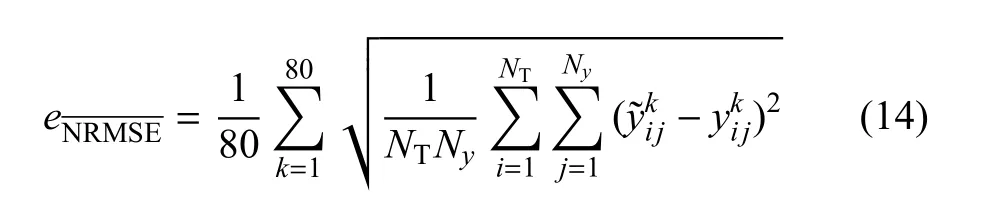
每次测试中,每种待测试响应面的参数均使用差分进化算法来最小化拟合误差,以避免参数选取不当导致的对比失真，对于SRBF和RBF两种方法优化过程的误差度量采取2.2节的定义.

测试结果总结在表2中，可以看出：

(1)SRBF在所有测试问题中的拟合精度较RBF明显提高；

(2)SRBF在部分测试问题中的拟合精度超过了以精度见长的Kriging响应面，并且这种拟合精度的优势随着采样点数目的增加越发明显.在采样点个数为20个时，SRBF在9个测试问题中仅有4个优于Kriging响应面，而当采样点数目逐步增加至80时，SRBF在8个问题的测试结果都优于Kriging响应面.

可以看出本文提出的对RBF响应面改进措施是可靠有效的.

表2 几种响应面插值精度验证Table 2 Examination of interpolation error of di ff erent response surfaces

3.2 HSADE优化效能验证

3.2.1 评价指标

(1)世代距离GD

世代距离表征了当前最优解集距理论最优解集的距离，是算法局部搜索效率的有效度量，按下式定义[22]

式中，Npf为当前优化结果最优解集中的解的数目，di为该最优解集中第i个解在目标函数空间距理论最优解集的最小欧氏距离，世代距离越小越好.

(2)超体积比HVR

超体积比表征了当前算法搜索到的结果占整个搜索空间的比例，是算法全局寻优能力的一种度量，定义如下[32]

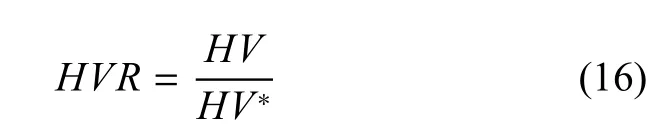
其中HV表示当前算法搜索结果在目标函数空间所能覆盖的超体积，定义为

HVi为以其中第i个个体和该优化问题各目标函数的最劣值构成的个体为对角的在目标函数空间的超立方体的体积，HV∗为理论最优解的超体积，超体积比越大越好.

3.2.2 HSADE优化效能验证

本文选择ZDT1-4，ZDT6，DTLZ1-4和DTLZ6问题[22-23]来验证HSADE的优化效能，作为对比参考的算法有MOPSO[34]，NSGA-II(二进制编码)和基本DE.

考虑到对测试集不同特性的要求，ZDT1-3问题的设计变量分别取30维和80维的版本，考察算法对高维问题的优化能力；ZDT4、ZDT6和DTLZ1-4、DTLZ6问题测试其10变量、2目标的情况，考察算法对复杂问题的优化能力，对于ZDT4问题，取其简化版本，令xi∈[0,1],i=2,3,···,10，其余参数范围不变.

参数设置方面，由于算法在不同问题中的表现依赖于参数选择，因此对于每种算法，本文应用多种参数组合以尽可能消除参数选择不当导致的性能衡量失准.对于DE，变异交叉模式采用/rand/1/Bi，其参数选择两组：①F=0.5,CR=0.2；②F=0.5,CR=0.7；对于NSGA-II，取其基因数恒定为8，变异率取4个不同值：0.01,0.02,0.05,0.10；交叉率恒定为50%，交叉方式为二进制交叉.对于MOPSO，令优化起始点随机生成，学习因子范围定为[1.0,2.0]，惯性权重取3个不同值，分别为0.4，0.6和0.8.

对于 HSADE，变异交叉模式采用/rand/1/targetto-best，自适应参数范围为F∈ [0.1,0.9]，CR∈[0.1,0.5]，Nb取为16.每代中响应面给出2个个体，空间增量填充给出1个个体.

为保证公平性以及减少随机因素的影响，对于包括 HSADE在内的每种算法采取随机初始化种群，对每个问题独立运行10次.每次优化过程每种算法共迭代32代，种群大小皆为32，总共约1024次函数评价.对于每次运行结果计算其世代距离和超体积比，取10次运行结果的中位数进行比较.

表3和表4给出了各优化问题的比较结果.

由表3可以看出，在世代距离表征的收敛性指标中，除问题DTLZ4中HSADE劣于NSGA-II，其余问题中HSADE都显著好于其他算法.

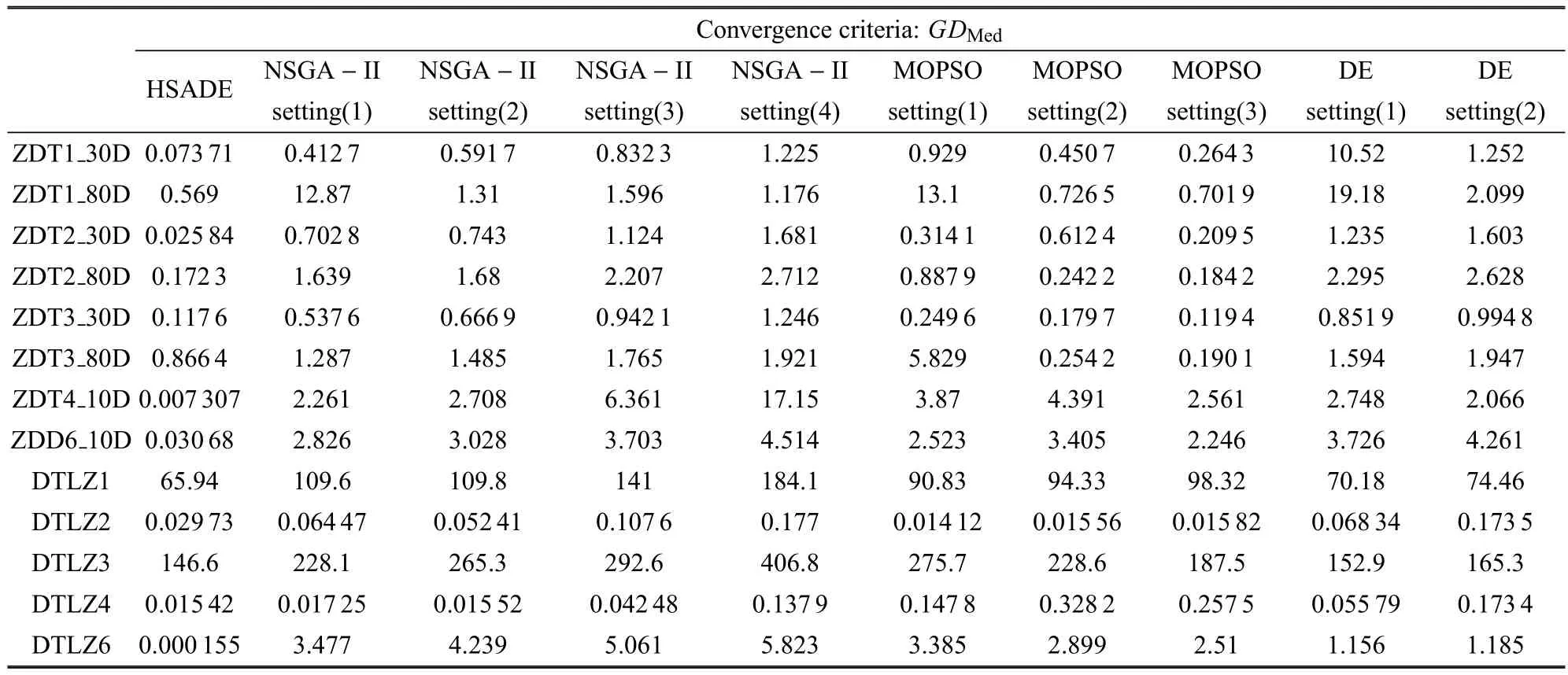
表3 几种算法在测试问题上的收敛性指标结果Table 3 Convergence criteria of competing algorithms upon tested problems

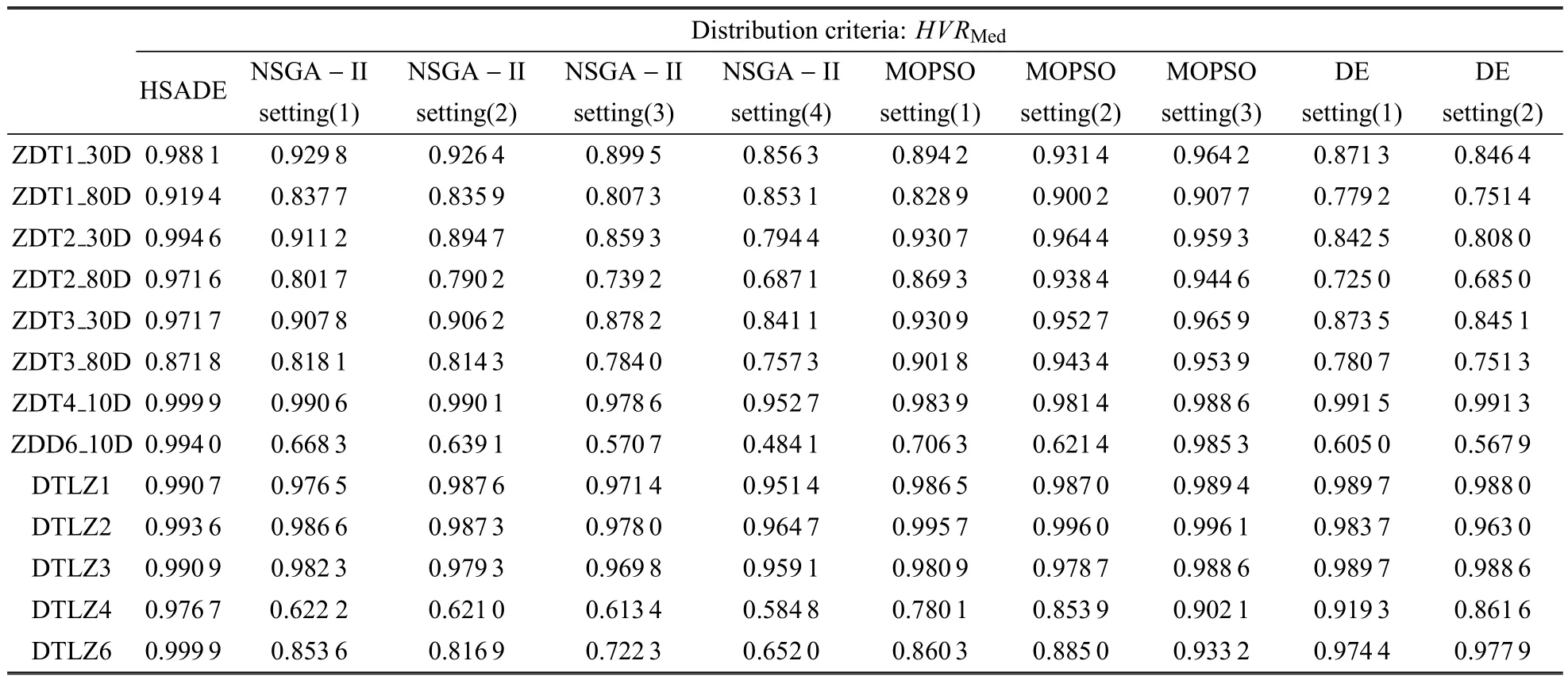
表4 几种算法在测试问题上的分布性指标结果Table 4 Distribution criteria of competing algorithms upon tested problems

由表4可以看出，在超体积比表征的分布性指标中，HSADE除了在 80维 ZDT3问题中劣于MOPSO，其余都优于其他算法.

从结果的比较可以看出,引入的 RBF响应面方法可以有效地提高算法的局部寻优能力，同时HSADE的混合结构也让其保留了较强的多样性保持能力，其综合优化能力较未经改良的DE有明显提高.

4 应用验证

为进一步验证HSADE在实际气动优化问题中的表现，本节展示应用HSADE，NARSGA[21](一种基于NSGA-II和Kriging响应面的混合算法)和传统差分进化算法解决两个典型气动优化问题的实际效果.

4.1 翼型优化

翼型优化是气动优化领域中较为基本和具有代表性的问题.本节展示应用以上3种算法对一个10%厚度的二维翼型在Ma=0.72和Ma=0.75两种工作状态进行减阻的具体效果.

优化问题中，翼型上下表面各设7个控制点，由CST(class shape function transformation)[35]曲线拟合生成.优化问题的详细描述总结于表5，其中Cd1和Cm1表示Ma=0.72工况下的翼型阻力系数和力矩系数，Cd2表示Ma=0.75工况下的翼型阻力系数，R为翼型前缘半径.优化起点选定10%厚度的RAE2822等一系列翼型，如图4(a)所示，其中Ref1-2为从课题组翼型库中选取的层流翼型.初始种群中，除手动输入的优化起点外，其余个体由1.1节所述的实验设计方法进行采样得到.

表5 翼型优化问题的优化变量、目标和约束Table 5 Variables,targets and constraints of the airfoil optimization problem

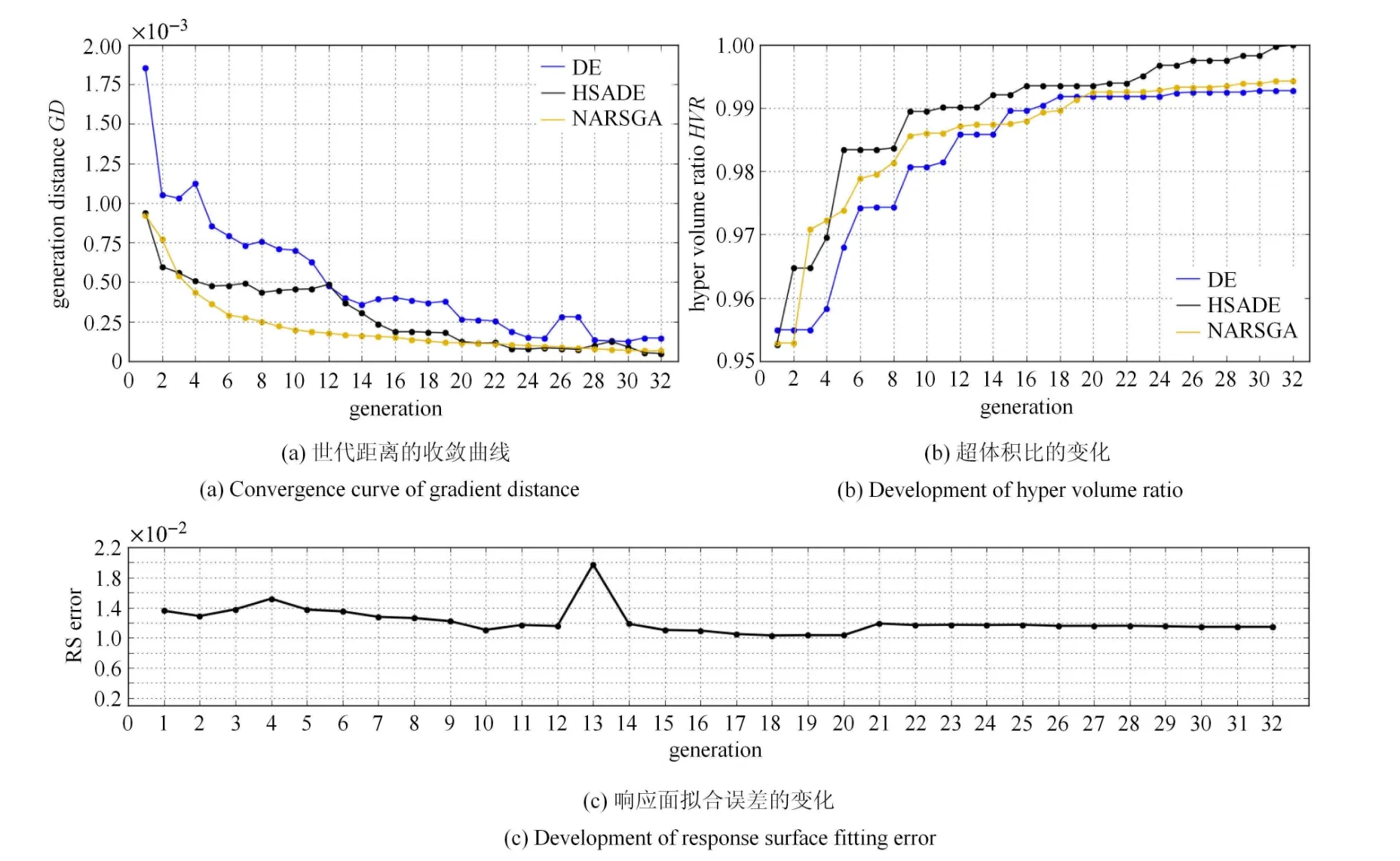
图4 优化进程Fig.4 Optimization progress

CFD计算采取定升力系数0.30，起始攻角1.5°，雷诺数取为1.50×107，马赫数取为0.72和0.75.湍流模式为两方程SST，离散格式为Roe格式，网格数约为3万，CFD计算使用NSAWET程序[36-37].

算法参数设置为：

(1)对于HSADE，CR定为0.2，F范围为[0.1,0.9]，每代由DE给出个体29个，ISF给出1个，RBF响应面给出2个，Nb为16；

(2)对于DE，CR定为0.2，F为0.5，其余设置等同于HSADE；

(3)对于NARSGA，取文献中默认参数.

每种算法优化总代数设为32代，种群大小皆为32，排除重复个体后各方法皆各进行了约1000次目标函数评估.3种算法优化过程中的世代距离收敛曲线，超体积比和响应面误差变化见图4，计算世代距离的参考最优解集取3种算法解集集合的非占优解.

3种算法优化得到的最优翼型与优化起点各翼型的几何外形对比见图5(b)～图5(d)中，每种算法在2种工况下的最小阻力个体表面压力分布对比见图6，图中c代表弦长.3种算法得到的Pareto前缘和优化起点中的最优性能翼型的对比见图7，3种方法得出的两种工况阻力最小值(图表中标注为minCd1和minCd2)和Pareto前缘中点个体(图表中标注为middle)的性能和对比优化起点的优化量见表6，从优化结果可以看出：

(1)从图4的优化过程看，HSADE的世代距离收敛速度明显强于未经改良的DE，在末端虽然存在振荡，但在优化末期仍保持对于NARSGA的轻微优势；在超体积比发展上，HSADE在整个优化过程中都明显领先于NARSGA和DE，显示出HSADE具有对目标函数空间更强的探索能力.另外在优化过程中HSADE的响应面的精度经校核处于较小的范围内，满足使用标准.

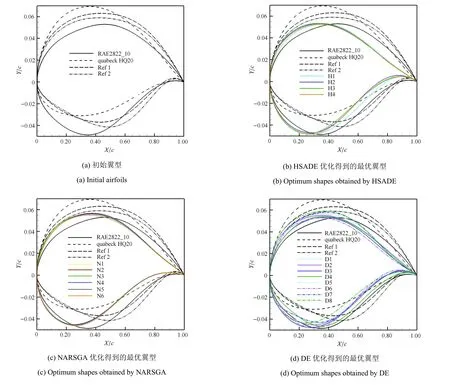
图5 初始外形和3种算法得到的外形Fig.5 Shapes of initial airfoil and optimal airfoils obtained by optimizers

图6 最优翼型表面压力分布形态Fig.6 Surface pressure distribution of optimal airfoils

(2)从图5看，在约束了升力的情况下，优化得出的最优翼型中，HSADE的结果在翼型下表面存在更大的差异性，表明了HSADE能够在优化过程中很好地保持种群的多样性，使优化进程不易发生停滞或早熟收敛.

(3)从表6和图7中看，HSADE得到的翼型在两个工况的阻力指标下都明显优于DE和NARSGA，在接近的CFD模拟次数下阻力优化量比另两种算法领先达0.5 count，HSADE得到的Pareto前缘明显优于另外两种方法.

(4)从压力分布上看，在两个工况下，在翼型前缘，和初始翼型压力分布相比3种算法得到的阻力最小个体的逆压梯度区有所缩小或完全消除；DE的结果在Ma=0.72工况下在下表面出现了二次加速的现象；Ma=0.75工况下，在翼型前缘HSADE和NARSGA的结果出现了一道微弱的激波，但它们在最大厚度前的压力分布较初始翼型更显合理，较大地减小了形阻和总阻力；两种工况下HSADE的结果压力恢复最为平稳，显示出较小的分离可能；综合来讲，该问题中HSADE和NARSGA的结果在压力分布上表现更好,相较于初始压力分布也有明显的改善.

图7 3种算法的Pareto前缘对比Fig.7 Comparisons of Pareto fronts obtained by HSADE,NARSGA and DE

表6 3种算法得到的最优翼型的性能参数和优化量Table 6 Performance and optimization measurement of the optimal airfoils obtained by optimizers

4.2 二维超声速喷管膨胀面优化

本小节展示使用以上3种算法对一个用于超声速推进系统的单斜面膨胀喷管(single expansion ramp nozzle,SERN)进行优化并对比其效果.在这个问题中，初始种群的产生依靠算法自身的采样方法进行.

图8展示了3种算法在优化过程中的世代距离收敛曲线，超体积比变化和HSADE的响应面误差变化，计算世代距离使用的参考解集仍取合并3种算法最优解集中的非占优部分.喷管构型参考文献[38].通过5个控制点使用NURBS(non-uniform rational B-spline)曲线拟合得到喷管上膨胀面的构型，下挡板(长度固定)的倾斜角可控，该构型见图9(a).喷管进口高度H0=0.5657m，出口高度H6=2.4m，长度Lt=3.294m，下挡板长度Lp=0.7m.

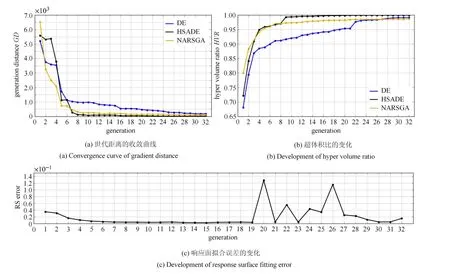
图8 优化进程Fig.8 Optimization progress

设计变量为 5个控制点的归一化高度Ci(i=1,2,3,4,5),下挡板倾斜角α.Hi由Ci表示为Hi=H0+Ci(H6-H0)，各设计变量的范围和起始个体A的参数由表7给出.

表7 喷管设计变量范围Table 7 Variable ranges of the nozzle design

喷管来流马赫数为 4.0，来流静温 2221.6K，来流静压 2516.6Pa，喷管入口马赫数 1.011，喷管入口总温和总压分别为T0=1673.6K和p0=144645Pa，湍流模式为两方程SST，离散格式为Roe格式，网格总量约为9万.

优化目标分别为推力T和俯仰力矩M，均要求最大化.每种算法进化总代数皆为32代，种群大小皆为32，对于每种算法，均计算了约1000个有效个体，算法参数设置和4.1节完全相同.

图9(b)～图9(d)展示了3种算法优化结果中3个比较有的代表性个体——推力最大个体(标记为maxT)、力矩最大个体(标记为maxM)和位于Pareto前缘的中点位置个体(标记为middle)的膨胀面形状.图10为3种算法得到的Pareto前缘，表7总结了3种算法得出的代表性个体的相关性能参数.

从优化结果可以得到如下结论：

(1)从图8看，在优化过程中HSADE的世代距离和超体积比皆明显领先于HSADE和DE，且HSADE的响应面误差尽管在优化后期存在波动，仍然保持在可以接受的范围内.

图9 喷管构型与3种算法获得的代表性个体外形Fig.9 Nozzle concepts and representative optimal shapes obtained by HSADE,NARSGA and DE

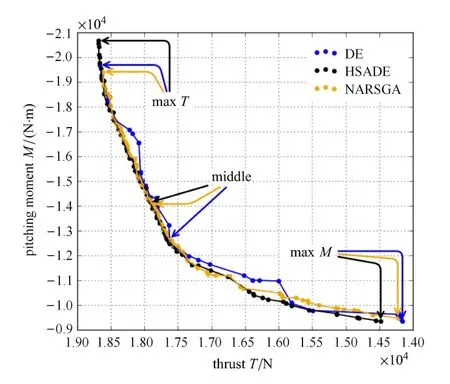
图10 3种算法的Pareto前缘Fig.10 Pareto fronts obtained by HSADE,NARSGA and DE

(2)从图9看，从推力最大过渡到力矩最大，3种方法得出的喷管型面变化趋势是一致的，同时HSADE和DE的结果中3种型面差异更大，可能表征了这两种方法具有更强的多样性保持能力.

(3)从图10和表8看，HSADE得到的最优解集最大推力和最大力矩均优于其余两种算法，且HSADE得到的Pareto前缘相较于另外两种方法也更加靠前；NARSGA得到的Pareto前缘和DE互有交叉，但其前缘个体更充足，整体上略优于DE.

表8 3种算法得到的代表个体的性能参数Table 8 Performance of representative optimal shapes obtained by HSADE,NARSGA and DE

5 结论

提出了一种混合优化策略，基于差分进化和RBF响应面形成了一种混合优化算法.并引入双败淘汰选择算子，参数自适应等加以进一步改进.大量测试表明：差分进化与径向基函数响应面的组合给出了一种可靠且实用的优化方法.能够在保持全局寻优能力的前提下在相近的总函数评估次数下达到更好的优化结果，对昂贵优化问题十分适用；与以往的混合优化算法相比，本文的算法在全局寻优能力和局部搜索能力均有明显提高.

1 Cheung S,Aaronson P,Edwards T.CFD optimization of a theoretical minimum-drag body.Journal of Aircraft,2015,32(1):193-198

2 卢文书，王帅培，马元春.基于CFD/CSD与Kriging插值模型的大展弦比复合材料机翼静气动弹性优化设计.应用力学学报，2015，32(4)：581-585(Lu Wenshu,Wang Shuaipei,Ma Yuanchun. Staticaeroelasticoptimizationofahigh-aspect-ratiocompositewing based on CFD/CSD and Kriging model.Chinese Journal of Applied Mechanics,2015,32(4):581-585(in Chinese))

3 Cazacu R,Grama L.Steel truss optimization using genetic algorithms and FEA.Procedia Technology,2014,12:339-346

4 Jones DR,Schonlau M,Welch WJ.Efficient global optimization of expensive black-box functions.Journal of Global Optimization, 1998,13(4):455-492

5 Su GS.Gaussian process assisted di ff erential evolution algorithm for computationally expensive optimization problems//Bilof R ed. Pacific-AsiWorkshop on Computational Intelligence and Industrial Application，PACIIA’08，Wuhan，2008.Los Alamitos：IEEE, 2008.272-276

6 Tabatabaei SME,Kadkhodaie-Ilkhchi A,Hosseini Z,et al.A hybrid stochastic-gradient optimization to estimating total organic carbon from petrophysical data:a case study from the Ahwaz Oilfield SW Iran.Journal of Petroleum Science&Engineering,2015,127(1): 35-43

7 孙美建,詹浩.Kriging模型在机翼气动外形优化中的应用.空气动力学学报,2011,29(6):759-764(Sun Meijian,Zhan Hao.Application of Kriging surrogate model for aerodynamic shape optimization of wing.Acta Aerodynamica Sinica,2011,29(6):759-764(in Chinese))

8 Huang D,Allen TT,Notz WI,et al.Global optimization of stochastic black-box systems via sequential kriging meta-models.Journalof Global Optimization,2006,34(3):441-466

9 Singh HK,Isaacs A,Ray T.A hybrid surrogate based algorithm (HSBA)to solve computationally expensive optimization problems.Evolutionary Computation,2014:1069-1075

10 Elsayed SM,Ray T,Sarker RA.A surrogate-assisted di ff erential evolution algorithm with dynamic parameters selection for solving expensive optimization problems.Evolutionary Computation,2014: 1062-1068

11 Liu B,Zhang QF,Gielen GGE.A Gaussian process surrogate model assisted evolutionary algorithm for medium scale expensive optimization problems.IEEE Transactions on Evolutionary Computation,2014,18(2):180-192

12 Antunes AP,Azevedo JLF.Studies in aerodynamic optimization basedongeneticalgorithms.JournalofAircraft,2014,51(3):1002-1012

13 Nam T,Chakraborty I,Gross J,et al.Multidisciplinary design optimization of a truss-braced wing concept//14th AIAA Aviation Technology,Integration,and Operations Conference，Atlanta，2014.Reston：AIAA,2014

14 Gibertini G.Aerodynamic shape optimisation of a proprotor and its validation by means of CFD and experiments.Aeronautical Journal, 2015,119(1120):1223-1251

15 Han ZH,Zimmerman R,Grtz S.Alternative cokriging method for variable-fidelitsurrogate modeling.AIAA Journal,2012,50(5): 1205-1210

17 Zingg DW,Nemec M,Pulliam TH.A comparative evaluation of genetic and gradient-based algorithms applied to aerodynamic optimization.European Journal of Computational Mechanics,2008, 17(1-2):103-126

18 Carrier G,Destarac D,Dumont A,et al.Gradient-based aerodynamic optimization with the elsA software//52nd Aerospace Sciences Meeting.2014,10:6.2014-0568

19 白俊强,王波,孙智伟等.基于松散式代理模型管理框架的亚音速机翼优化设计方法研究.西北工业大学学报,2011,29(4):515-519(Bai Junqiang,Wang Bo,Sun Zhiwei,et al.Developing optimization design of subsonic wing with loose type of agent model.Journal of Northwestern Polytechnical University,2011,29(4): 515-519(in Chinese))

20 Kim HJ,Liou MS.Aerodynamic optimization using a hybrid moga-local search method//51st AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference 18th AIAA/ASME/AHS Adaptive Structures Conference 12th,2010: 2911

21倪昂修,张宇飞,陈海昕.NSGA-Ⅱ算法的改进及其在多段翼型缝道参数优化中的应用.空气动力学学报,2014,32(2):252-257(Ni Angxiu,Zhang Yufei,Chen Haixin.An Improvement to NSGA-II algorithm and its application in optimization design of multi-element airfoil.Acta Aerodynamica Sinica,2014,32(2):252-257(in Chinese))

22 Deb K,Pratap A,Agarwal S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-II.IEEE Transactions on Evolutionary Computation,2002,6(2):182-197

23 公茂果,焦李成,杨咚咚等.进化多目标优化算法研究.软件学报, 2009,20(2):271-289(Gong Maoguo,Jiao Licheng,Yang Dongdong,et al.Research on evolutionary multi-objective optimization algorithms.Journal of Software,2009,20(20):271-289(in Chinese))

24 Zitzler E,Laumanns M,Thiele L.SPEA2:improving the strength pareto evolutionary algorithm.Eurogen,2001,3242(103):95-100

25 Storn R,Price K.Di ff erential evolution:a simple and efficient adaptive scheme for global optimization over continuous spaces.Journal of Global Optimization,1995,23(4):341-359

26 Park J,Sandberg IW.Universal approximation using radial-basisfunction networks.Neural Computation,1991,3(2):246-257

27 穆雪峰,姚卫星,余雄庆等.多学科设计优化中常用代理模型的研究.计算力学学报,2005,22(5):608-612(Mu Xuefeng,Yao Weixing,Yu Xiongqing,et al.A survey of surrogate models used in MDO.Chinese Journal of Computational Mechanics,2005,22(5): 608-612(in Chinese))

28 Wang L,Huang FZ.Parameter analysis based on stochastic model for di ff erential evolution algorithm.Applied Mathematics&Computation,2010,217(7):3263-3273

29 Brest J,Greiner S,Boskovic B,et al.Self-adapting control parameters in di ff erential evolution:a comparative study on numerical benchmark problems.IEEE Transactions on Evolutionary Computation,2007,10(6):646-657

30 Rippa S.An Algorithm for selecting a good value for the parameter c in radial basis function interpolation.Advances in Computational Mathematics,1999,11(2):193-210

31 吴亮红.动态差分进化算法及其应用.北京:科学出版社,2014: 190-220(Wu Lianghong.Dynamic Di ff erential Evolution and its Application.Beijing:Science Press,2014:190-220(in Chinese))

32 Nebro AJ,Luna F,Alba E,et al.Abyss:adapting scatter search to multiobjective optimization.IEEE Transactions on Evolutionary Computation,2008,12(4):439-457

33 Deb K,Thiele L,Laumanns M,et al.Scalable test problems for evolutionary multiobjective optimization//Abraham A,Jain L,Goldberg Reds.EvolutionaryMultiobjectiveOptimization.London:Springer London,2005.105-145

34 Coello CAC,Lechuga MS.MOPSO:a proposal for multiple objective particle swarm optimization//Proceedings of the 2002 Congress on Evolutionary Computation，CEC’02，Honolulu,Hawaii，2002. Los Alamitos：IEEE,2002.2:1051-1056

35 Kulfan BM,Bussoletti JE.Fundamental parametric geometry representations for aircraft component shapes//11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference，Portsmouth, Virginia，2006.Reston：AIAA，2006.6948

36 Chen HX,Fu S,Li FW.Navier-Stokes simulations for transport aircraft wing/body high-lift configurationsJournal of Aircraft,2003, 40(5):883-890

37 Zhang YF,Chen HX,Fu S.Improvement to patched grid technique with high-order conservative remapping method.Journal of Aircraft,2012,48(3):884-893

38 陈兵,徐旭,蔡国飙.二维超燃冲压发动机尾喷管优化设计.推进技术,2002,23(5):433-437(Chen Bing,Xu Xu,Cai Guobiao.Optimization design of two dimensional scramjet nozzle based on N-S equations.Journal of Propulsion Technology,2002,23(5):433-437(in Chinese))

HYBRID OPTIMIZATION ALGORITHM BASED ON DIFFERENTIAL EVOLUTION AND RBF RESPONSE SURFACE1)

Deng Kaiwen Chen Haixin2)
(School of Aerospace Engineering，Tsinghua University，Beijing100084，China)

A new hybrid optimization algorithm HSADE(hybrid self-adaptive di ff erential evolution)based on di ff erential evolutionandradialbasisfunctionresponsesurfacewasproposedaimingataerodynamicoptimizationproblems.Through combing the merits of response surface method’s fast local searching ability and di ff erential evolution’s powerful global searching ability,the overall local and global search efficiency of HSADE were simultaneously enhanced.Several improvements were made on certain logics and strategies embedded in the processes of each sub-algorithm by proposing and utilizing strategies such as selection strategy based on double elimination and self-adaptive parameters.Having applied HSADE and several other typical optimization algorithms—NSGA-II,MOPSO and multi-objective di ff erential evolution to several benchmark functions,the results indicated HSADE was superior to other algorithms in most of the cases regarding local search ability represented by generation distance and global search ability symbolled by hyper volume ratio,which validated the e ff ectiveness of above improvements.Applying HSADE along with basic DE and NARSGA to an airfoil optimization problem and a hypersonic nozzle expansion surface optimization problem,the results showed HSADE was able to obtain airfoils with extra 0.5 count drag reduction and nozzles with better performance than othertwo algorithms under approximately 1000 function evaluations,which indicated high engineering application potential of HSADE.

di ff erential evolution,response surfaces,computational flui dynamics,multiobjective optimization,optimization design

V211.3

A

10.6052/0459-1879-16-285

2016–10–17收稿，2017–01–16录用,2017–01–20网络版发表.

1)中航工业产学研专项(cxy2014QH14)和清华大学自主科研计划(2015THZ0)资助项目.

2)陈海昕，教授，主要研究方向：空气动力学，计算流体力学.E-mail：chenhaixin@tsinghua.edu.cn

邓凯文,陈海昕.基于差分进化和RBF响应面的混合优化算法.力学学报,2017,49(2):441-455

Deng Kaiwen,Chen Haixin.Hybrid optimization algorithm based on di ff erential evolution and RBF response surface.Chinese Journal of Theoretical and Applied Mechanics,2017,49(2):441-455