鹅掌楸树叶在风中的变形与振动1)
邵传平 朱园园
(中国计量大学流体检测与仿真研究所,杭州310018)
鹅掌楸树叶在风中的变形与振动1)
邵传平2)朱园园
(中国计量大学流体检测与仿真研究所,杭州310018)
树叶的空气动力与流固耦合特性研究在树木保护、新发电技术开发、太阳能帆板设计等方面具有重要意义.Vogel首次发现树叶在较高风速下具有形状重构以避免受损害的能力.Vogel实验时叶柄端部是简支的,与叶柄与树枝的自然连接方式不同.在本文的研究中,叶柄端部是固支的,叶片垂直悬挂,正面或反面迎风.在风速0~27m/s范围内,存在两种叶片静止状态,即飞翼形稳定和锥形稳定;还有3种叶片振动状态,即低频摆动、第1和第2高频振动.这5种状态由5个临界风速决定.通过70余片树叶测试结果的统计,得到了树叶每个状态存在的概率,及每个临界风速的期望值.流动显示发现树叶变形后其尾流中存在旋涡脱落现象.天平测量发现叶片阻力系数随叶片雷诺数的增大而减小并逐渐接近于0.1.引入悬臂梁模型,采用测量的叶片气动力,对叶柄静态弯曲形状进行计算,结果表明当风速由0逐渐增至5m/s时,叶柄向下游弯曲迅速;但风速由5m/s进一步增大时,向下游的弯曲则变慢.
树叶,形状重构,振动,临界风速
Key words tree leaves,reconfiguration vibration,critical wind speed
引言
树叶在大风中具有良好的弯曲变形能力[1],其气动与流固耦合特性的研究在仿生学[2]、新发电技术[3]、建筑设计[1]、太阳能帆板设计[4]以及树木保护[5]等方面具有参考意义.
Vogel[6]对红枫、鹅掌楸、核桃等多种树叶做了风洞实验研究,首次发现树叶在高风速下具有将叶片重构成锥形以减小空气阻力,达到自我保护的能力.此后研究者对各种植物叶的形状重构现象进行了研究.Miller等[7]在水槽中对野生姜叶和野生紫罗兰叶进行实验,发现这些植物叶片在较高流速下同样卷成锥形;在未卷成锥形时,其尾流中具有强烈的旋涡脱落,而卷成锥形后,旋涡脱落减弱.Speck[8]研究了芦竹在风中的形状重构及迎风面积变化.人造树叶或人造柔性体同样具有形状重构的能力.Schouveiler等[9]将一个塑料圆片沿一条径线剪开并在圆心处固定,来模拟树叶形状,发现它在风中能卷成锥状,并得到了锥角随风速的变化.Alben等[10]研究了一维柔性体在液流中的自相似弯曲变形.Gosselin等[11]研究了丝线束群(花朵形多孔柔性体)在风中的形状重构.Shelley等[12]研究了(丝线和旗子)在肥皂泡膜液流中的稳定性与旋涡脱落形式,并在质量和刚度坐标系中得到了失稳的临界线.
阻力方面,Albayrak等[13]测试了甜茅叶与茎在水中的阻力系数随雷诺数的变化,并研究了叶片长宽比的影响.Speck[8]发现芦竹叶阻力随风速呈线性增大.Schouveiler等[9]研究了沿径向开缝的塑料圆片阻力系数与所卷成锥角的关系.Alben等[10]发现一维柔性体的自相似变形使其阻力减小.Vogel[6]测试了多种阔叶树树叶的阻力,发现与刚体阻力明显不同,树叶阻力D与风速U具有关系:D~U2+α,α被称为Vogel系数.Vogel[6]测试了杨槐、黑胡桃、山核桃、红枫、鹅掌楸及白橡树等6种树叶及山核桃小叶,得到的α值除白橡树叶外,均为负值,在-0.2~-1.18之间,平均为-0.71.Vogel[6]还研究了复叶(cluster)的阻力,发现红枫、鹅掌楸、白橡树、白杨和栎树等复叶的α值在-0.44~-1.06之间,其平均值与单树叶平均值几乎相同.应当指出,柔性体的变形并不总是引起阻力减小,有时也引起阻力增大,比如旗子在风中飘动时的阻力远比刚性平板顺流放置时大[14],因此树叶减阻的机制值得仔细研究.
上述研究中,都是将叶柄或茎端部自由支撑,叶柄可绕端部转动,因此叶片从较小风速或流速开始就处于顺流方向,风向角为0°.自然生长的植物,其叶柄端部与枝条之间是固接的,不能自由转动,因此即使在较高风速下,叶片也不会处于顺流方向.同一颗树上的树叶,叶片角各不相同.Posada等[15]测量得到热带树冠上叶片角(叶片法线与垂直方向的夹角)在 0°~45°之间变化.Pisek等[16]研究了不同国家的多种阔叶树,发现为了获得更好的光照条件,叶片角可在0°~90°范围内变化,但不同树种叶片角的分布几率有较大差别.McNeil等[17]测量了5种树叶的叶片角在0°~90°范围内的概率分布. Hernandez[18]发现沿向日葵主杆向上端,叶柄角(与水平面夹角)由-9°增大到60°,叶片角(与水平面夹角)由1°减小到-60°.树叶在树枝上的排列分为对生、互生和螺旋生3种.除了叶片角外,绕枝条的周角也有变化.对生、互生叶片周角相差180°,螺旋生叶片周角变化范围则在0°~360°之间.其他与叶片角相关的研究见文献[19-22].
同一颗树在同一个均匀风场中,各个叶子的叶片角和周角千差万别,风向角也就各不相同.其中与叶片顺流方向差别最大的,是叶片垂直于来流的情况.叶片垂直来流的情况又可分为树叶垂直悬挂和非垂直悬挂两种状态,每种状态又分为树叶正面(光照面)迎风和反面(背阴面)迎风两种情况.由于常见树叶都呈曲面形状,正面凹进,反面突出,两面迎风的气动特性有差别,需要研究.
造成叶片垂直悬挂与非垂直悬挂之间差别的是重力因素的影响.当树叶非垂直悬挂时,由于自身重量,叶柄及叶片局部存在一定程度的弯曲,会影响叶片风向角.树叶垂直悬挂时,重力不会造成叶片弯曲,因此不会影响叶片风向角.
Niklas[23]测量了2个树种的简单叶片和3个树种的复叶,发现单位面积叶片的重力近似为1N/m2. Scholes等[24]测量的16种沙漠树叶的单位面积重量在0.8~2.5N/m2之间.这些树叶的最大重力小于1.5m/s的风速垂直吹过叶片时的空气阻力.因此,对于叶柄和叶片刚度相对较大的鹅掌楸树叶,重力影响很小,可以忽略.
叶片顺着流向放置时,气流的摩擦阻力占主要位置,升力和侧向力很小.此时叶柄与顺流呈直线,很少弯曲,产生大幅振动的几率很小.叶片垂直来流放置时,流动出现分离,压差阻力占主要位置.更重要的是会出现强烈的旋涡脱落现象,伴随着侧向力的周期性变化.随着风速增大,叶柄逐渐向下游方向弯曲,升力使叶片逐渐抬升,叶片风向角则逐渐减小.Shao等[25]发现,当连枝的悬铃木树叶垂直悬挂时,除了出现形状重构现象外,在不同风速下会出现低频摆动和高频振动现象.树叶的这些振动状态在顺流向放置时没有出现[6].
其他树种的树叶在叶柄端部固支和垂直悬挂时有没有振动和形状重构现象发生?发生这些现象的临界风速多大?树叶气动阻力怎样变化?本文将对鹅掌楸树叶的这些气动特性进行探讨.
1 实验材料与方法
鹅掌楸树叶的特点,一是叶柄较长,横截面呈近似圆形,长度方向有较小锥度,二是叶片上半部分较宽,下半部分较窄,宽度在腰部突然变化.叶片有4个尖角,分别位于腰部和下端两侧,边缘其他部分圆滑.树叶尺度如图1所示.

图1 鹅掌楸树叶及其叶片与叶柄尺寸Fig.1 Tulip leaf and dimensions of its lamina and petiole
树叶的变形与振动过程由一台数字摄像机记录,摄像帧率为50fps.树叶尾流的纵向流动情况由烟线法进行流动显示.尾流横向流动由PIV测量和显示,采样频率为10Hz.树叶3个方向的瞬时气动力和3个方向的瞬时力矩用六分力天平测量,采样频率为5kHz.
实验用新鲜鹅掌楸树叶是5月中旬在中国计量大学校园附近采集.实验选用的单片树叶及其叶柄位于树枝的末端.测试的树叶共计73片,都是随机从树上采集,并且采集后立即放于常温水中保鲜待用.采集树叶的叶片面积概率密度接近于正态分布,如图2所示.叶片与叶柄的尺度变化范围基本概括了所在地区鹅掌楸树叶的自然变化范围,具有较好的代表性.
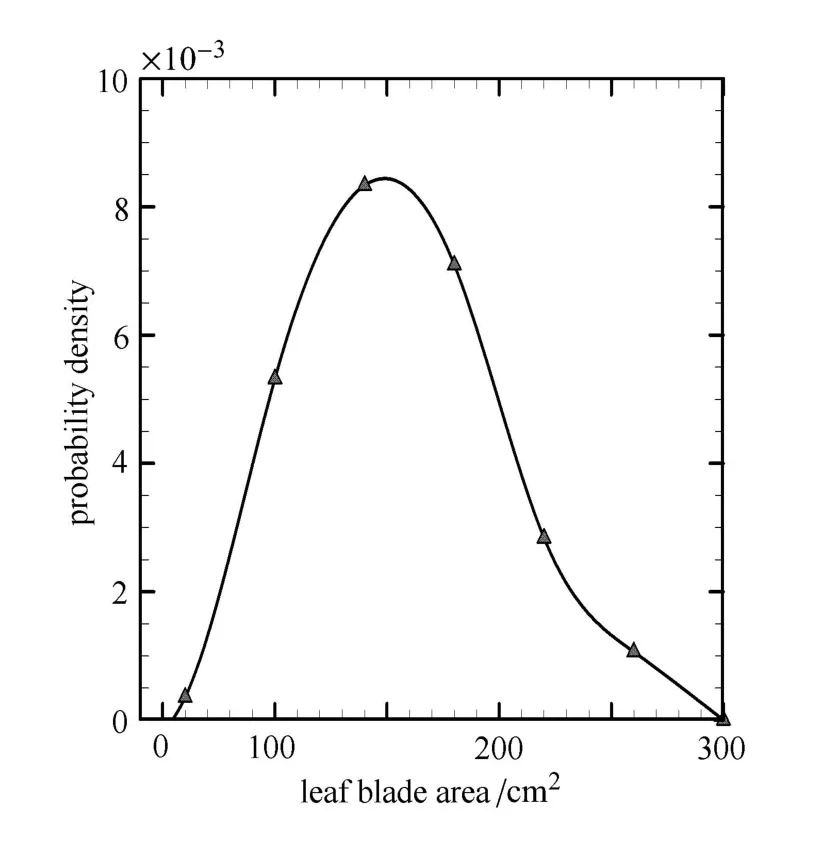
图2 所测试树叶叶片面积的概率分布Fig.2 Probability density of lamina area of the tested tulip leaves
实验在中国计量大学循环式风洞中进行.风洞试验段长度为2m,横截面为0.6m×0.6m的正方形,能够提供速度为0.5~35m/s,湍流度小于0.4%的均匀风速.
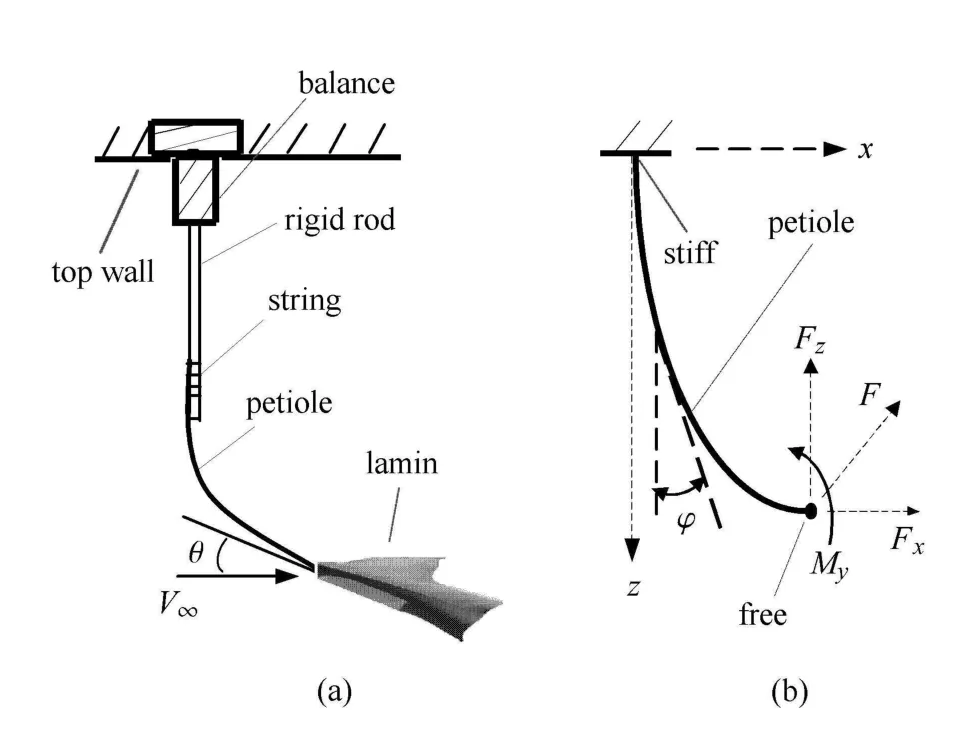
图3 (a)叶片悬挂于风洞中,(b)集中力作用于叶柄悬臂梁模型Fig.3 Sketch of(a)the leaf in wind tunnel,and(b)concentrated aerodynamic load on cantilevered beam model of the petiole
如图3所示,在风洞顶壁上开一圆孔,将风洞六分力天平主体由外侧通过圆孔伸入风洞中,而天平底座由螺栓固定于洞壁.一根长度0.2m,直径为6mm的不锈钢棒,垂直放置于风洞中,其上端由螺丝扣固接于天平上.用细丝线将叶柄端部牢固地绑在钢棒下端,使树叶呈自然垂挂状态.对每片树叶的正面迎风和反面迎风分别测试.测试时风速由0逐步增大,直至27m/s为止.当风速较低时,每次增量为0.5m/s,当风速超过4m/s以后,每次增量至1m/s.风洞每增大一次风速,都要先稳定约20s,然后采集数据.
2 实验结果与分析
2.1 树叶的风振状态与临界风速统计
对 73片鹅掌楸树叶进行了反面迎风测试.图4是树叶在反面迎风时的典型状态变化.风速很小时,树叶静止.当风速增大到V1=3.7m/s时,树叶出现低频大幅的左右摇摆,有时还伴随着绕叶柄轴线的扭转振动[26].风速增大到V2=5.6m/s时摆动停止,叶片呈飞翼形状并处于稳定状态,这是第1种气动平衡.当风速增大到V4=11.4m/s时,叶片卷缩成锥形,阻力大为减小,叶片静止,这是第2种气动稳稳定状态.当风速继续增大到V3=8.3m/s时,飞翼形稳定平衡状态被打破,叶片出现大幅高频振动.叶片在振动状态中不断改变形状,以寻求新的气动定状态.随着风速进一步增大,第二种稳定状态一直持续.直到风速达到V5=22m/s,平衡才被打破,叶片失稳,再次出现高频振动.将开始出现低频摆动、飞翼形稳定、第1高频振动、锥形稳定、第2高频振动的风速分别称为第1,2,3,4和第5临界风速,并分别用V1,V2,V3,V4和V5表示.

图4 叶片反面迎风时其状态随风速的变化Fig.4 The back surface facing the wind:status changes with wind speed
对70片树叶进行了正面迎风测试.与反面迎风情况类似,典型情况下,随着风速由小变大,树叶也依次出现上述5种状态,以及5个临界风速.
叶片正面迎风时,出现两种不同的变化过程,第1种:低频大幅摆动停止以后,由于叶柄的扭转,叶片变为反面迎风并呈飞翼状,且在此后与反面迎风的典型状态变化相似,这在测试的70片树叶中有21片属于第一种情况,占30%.第2种:正面始终为迎风面,随着风速增大,也经历低频摇摆、飞翼形、高频振动、锥形、再次振动等状态,这在测试的叶片中占70%.
叶片正面迎风的典型稳定状态如图5所示.正面迎风时的飞翼形状,除了叶片两侧上卷(图5(a))外,还存在向下翻卷的情况(图5(b)).与反面迎风的锥形其主叶脉位于下侧(图4(e))不同,正面迎风的锥形其主叶脉可位于上侧(图5(c)).
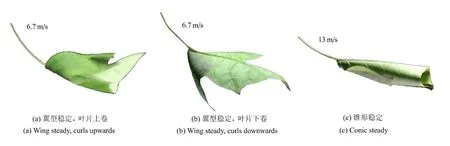
图5 两种不同的稳定形状Fig.5 Two types of steady states
需要指出的是,并不是每个叶片都经历上述全部5种状态.表1和表2分别是各临界风速和各状态存在的概率.正面迎风时的情况是:第1临界风速和低频摆动存在的概率均为92.7%.未出现低频摆动的7.3%叶片中,4.3%通过静态变形逐渐形成飞翼形稳定,3.0%通过叶片弯曲方向由向前突然改变为向后形成飞翼形稳定.

表1 正面F和反面B迎风时各临界风速存在的概率Table 1 Probability of existence of each critical wind speed, F-front surface facing wind,B-back surface facing wind

表2 正面F和反面B迎风时各状态存在的概率Table 2 Probability of existence of each status,F-front surface facing wind,B-back surface facing wind
突变为飞翼形的第 2临界风速存在的概率为91.4%,其中88.4%由低频摆动突变,3.0%由叶片弯曲方向突变而形成飞翼形,加上渐变而成的4.3%,能够形成飞翼形稳定状态的叶片概率为95.7%;而其他4.3%随着风速增大,由低频摆动逐渐变化为高频振动.
由飞翼稳定突变为第1高频振动的第3临界风速存在的概率为70%,第1高频振动存在的概率为70%+4.3%=74.3%.25.7%叶片不存在高频振动,由飞翼形稳定突变为锥形稳定.
第 4临界风速与锥形稳定存在的概率均为88.6%,其中62.9%由高频振动突变为锥形稳定,其余25.7%由飞翼形稳定突变为锥形稳定.11.43%叶片不存在锥形稳定,由第1高频振动直接过渡到第2高频振动.
由锥形稳定突变为第2高频振动的第5临界风速存在的概率为67.1%.加上一直振动的11.4%,第5临界风速以后,处于高频振动的叶片占78.6%,其他21.4%的叶片保持锥形静止直到实验最高风速.
反面迎风的情况:只有13.7%的叶片存在第1临界风速(出现低频摆动),其余叶片通过静态变形逐渐变为飞翼形.有11.0%存在第2临界风速,而形成飞翼形稳定的概率高达97.3%,其中11.0%从低频摆动突变而来,其他86.3%由静态变形逐渐形成.有87.7%的叶片存在第3临界风速(由飞翼形突变为高频振动),加上由低频摆动逐渐变化为高频振动的2.7%,叶片出现高频振动的概率为90.4%.存在第4临界风速的叶片占49.3%,而存在锥形稳定状态的占54.8%,其中4.1%由飞翼形突变为锥形,45.2%由高频振动突变为锥形,还有5.5%通过静态变形逐渐变成锥形.其他45.2%由第1高频逐渐过渡到第2高频振动,未能形成锥形稳定.第5临界风速(由锥形突变为第2高频振动)存在的概率为30.1%.加上45.2%由第1到第2高频逐渐过渡的部分,第5临界风速以后叶片高频振动的占75.3%,其余24.7%的叶片保持锥形稳定至实验最高风速.
为了了解临界风速的分布情况,按照如下公式算出某个临界值V处的概率密度分布
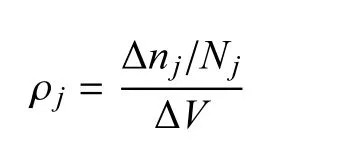
其中下标j代表第j个临界风速,Nj为实验中存在的第j临界风速的总个数,∆V为一个小的速度间隔,∆nj代表位于区间[V-0.5∆V,V+0.5∆V)内的第j临界风速的个数.统计中实际采用的∆V=1m/s.
图6为叶片正面迎风时各临界风速的概率密度分布.前两个临界风速分布比较集中,后3个则比较分散.除了第4临界风速为双峰外,其他均为单峰,接近于高斯分布.反面迎风时也有类似的分布.
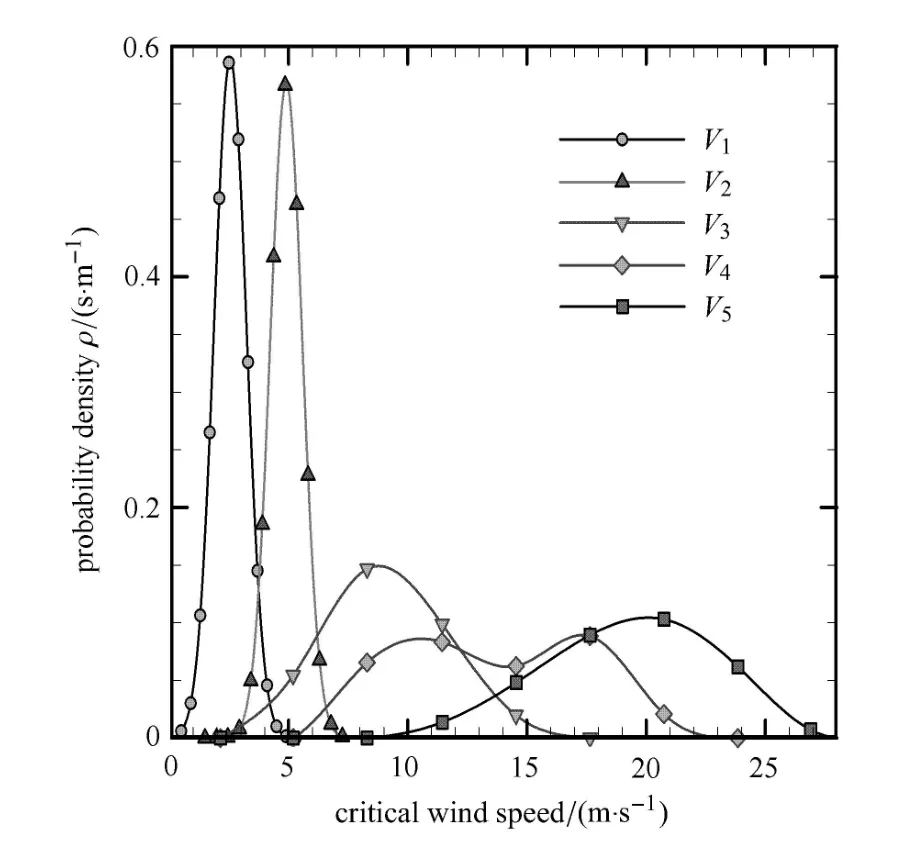
图6 叶片正面迎风时各临界风速的概率密度Fig.6 Probability densities of the critical wind speeds,with the front leaf surface facing wind
正面和反面迎风时各临界风速的期望值如表3所示.可知除第5临界风速外,正面迎风时各临界风速均比反面迎风时小,这是自然状态时叶片存在一定弯曲,正面迎风比反面迎风时钝度大,所受气动阻力更大,叶柄弯曲变化更快,因而更早进入振动状态.

表3 正面F和反面B迎风时各临界风速期望值Table 3 Expected values of each critical wind speed F-front surface facing wind,B-back surface facing wind
2.2 树叶尾流旋涡脱落
流体以一定速度流过钝体时,会在钝体两侧交替地产生旋涡脱落,使两侧的流体压力分布产生周期性变化,从而形成一个横向交变力作用于钝体,引起钝体振动[27-29].当物体展向尺度一定时,改变其横向尺度,会同时产生两种相反的作用.一方面,横向尺度减小,会减小局部横向交变力的幅值,从而使作用于整个物体的合力幅值减小.另一方面,横向尺度减小,物体的展向尺度与横向尺度之比增大,流动的二维性增强,各展向位置旋涡脱落的频率和相位的一致性增强,作用于物体的合力增大.
当风速较小时,树叶叶片变形较小,树叶尖锐的边缘引起流动分离,因此是钝体绕流.风速较小时,树叶表面正对着来流,风向角接近90°,横向尺度最大.
如图7,当叶片反面迎风时,随着风速增大,叶柄向下游弯曲,叶片向后上方抬起,两侧叶片向上翻卷,形成飞翼形.随风速增大,叶片主叶脉呈直线,叶片长度不变,而由于叶片卷起,侧向(垂直于纸面方向)迎风尺度减小.叶片宽度较大的地方,卷起的程度较高,宽度较小的地方,卷起的程度较低,从而使叶片的迎风宽度趋于均匀,流动的二维性增强.
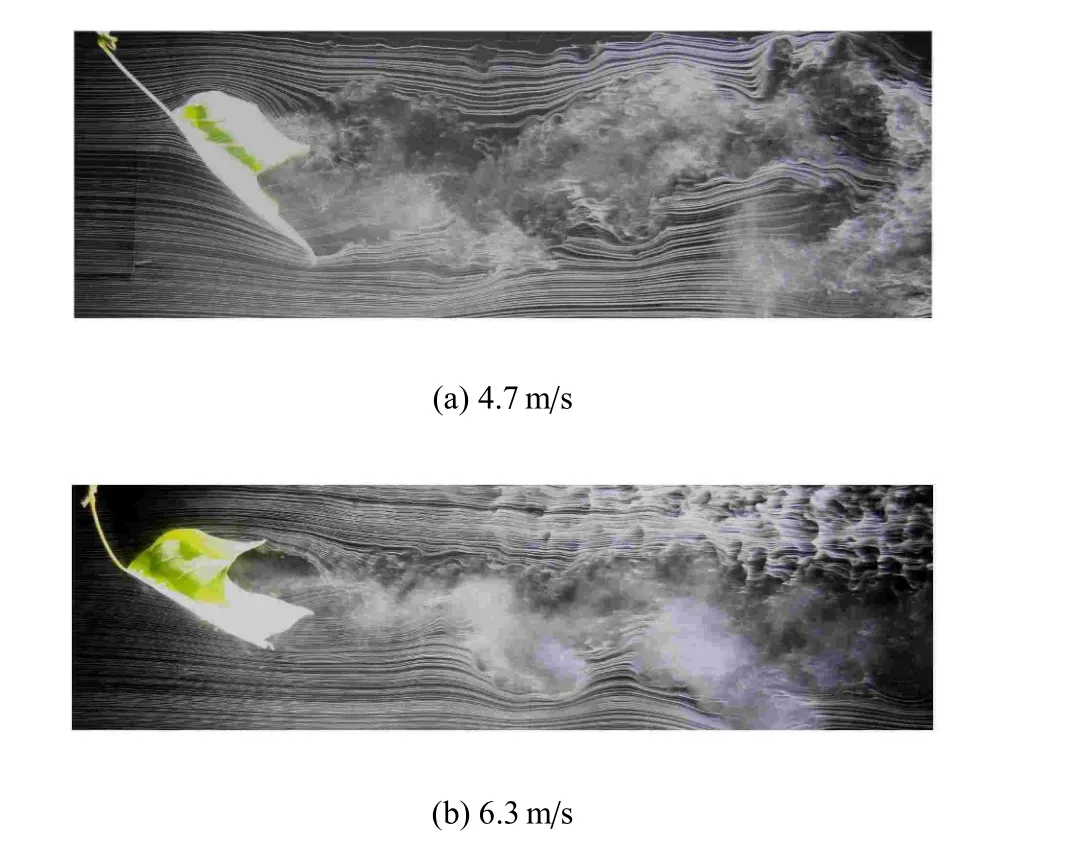
图7 反面迎风时树叶的形状、方位及尾流变化侧图Fig.7 Side view of the shape,orientation and wake of the leaf with its back surface fcaing wind

图7 反面迎风时树叶的形状、方位及尾流变化侧图(续)Fig.7 Side view of the shape,orientation and wake of the leaf with its back surface fcaing wind(continued)
随着风速改变,树叶形状和叶片角发生变化,但树叶尾流中总是存在旋涡脱落现象.从侧视图7可以看到树叶下侧存在旋涡.叶片左右两侧的旋涡从下游往上游看会更清楚.图8为竖直固定杆下游40cm处横截面上的时均横向流动图.横向流动中存在两个旋转方向相反的涡,是叶片两侧旋涡脱落在下游横向流动的反映.根据Roshko[27],物体下游旋涡的尺度与物体侧向平均迎风尺度成正比.
2.3 树叶气动阻力
根据天平测量的气动力数据可以得到树叶时均气动阻力系数Cd随叶片雷诺数的变化.这里,阻力系数和雷诺数的定义分别为
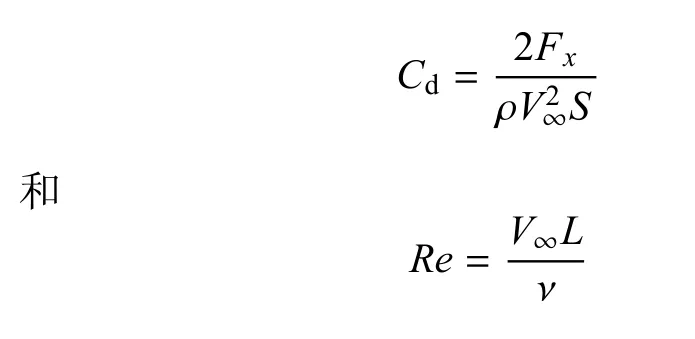
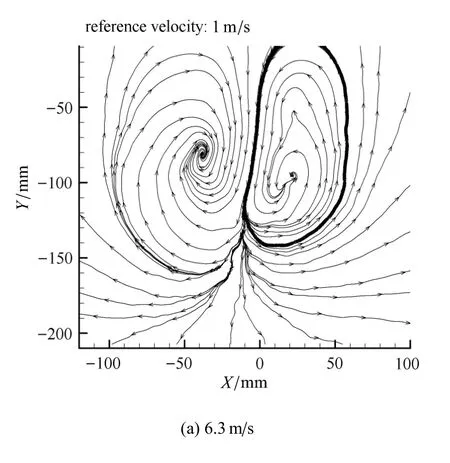

图8 在叶柄固定棒下游0.4m处测量的树叶尾流的横向流动图案Fig.8 Upstream view of the transverse fl w 0.4m downstream of the leaf
其中,Fx为树叶流向时均力,ρ为空气密度,V∞为风速,L为叶片长度,S为叶片面积,ν为空气运动黏度.
图9为叶片正面迎风时,7片不同尺度树叶的阻力随雷诺数的变化情况.可知当雷诺数(风速)较小时,由于叶片形状等的差异,各叶片阻力系数之间有一些差别.当雷诺数(风速)较大时,叶片都卷成锥形,阻力系数均趋近于同一个常数,约为0.1.值得注意的是,树叶振动的发生,能使脉动阻力系数增大,但叶片时均阻力系数没有明显变化.
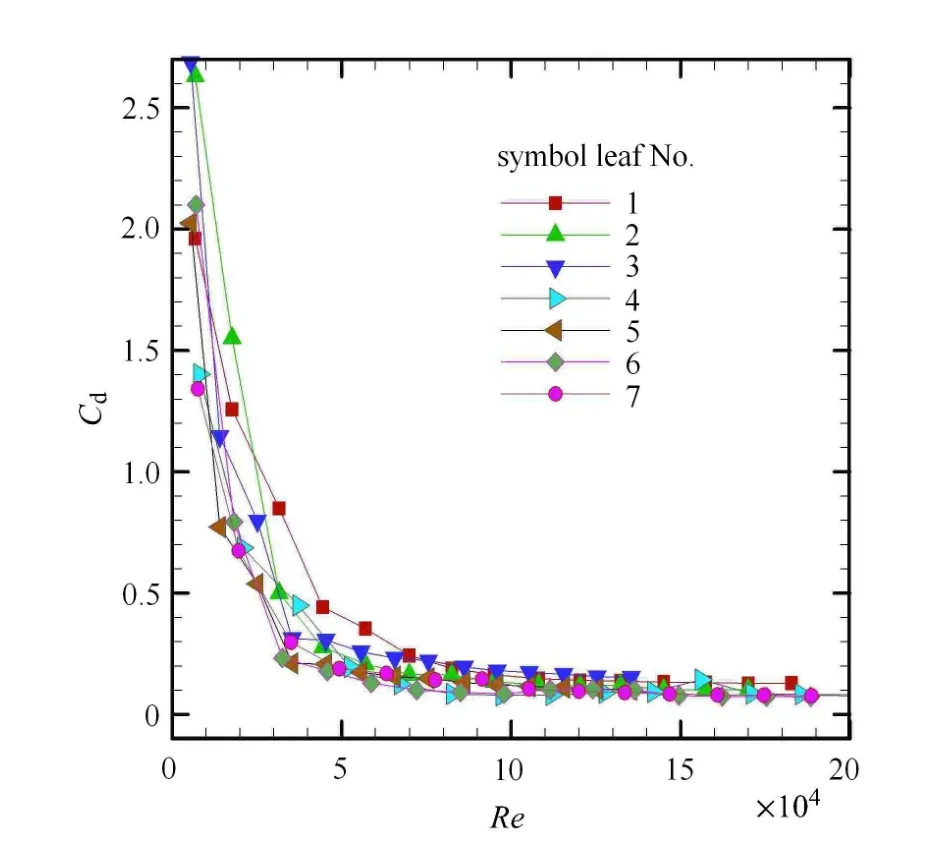
图9 正面迎风时各叶片阻力系数随雷诺数的变化Fig.9 Drag coefficients of leaves vs Reynolds number,with the front surface facing wind
2.4 叶柄的静态弯曲
在时均气动力作用下,叶柄发生弯曲变形.如图3(b)所示,叶片所受的气动力可分为流向力Fx,垂直向上的升力Fz,以及侧向力Fy.忽略叶片质量力时,作用于叶柄自由端的力,除Fx,Fy,和Fz外,还有力矩Mx,My和Mz.其中时均力Fx及其对y轴的力矩My较大,其他力和力矩的时均值都较小,因此叶柄主要在xz平面发生弯曲,而在y方向的弯曲较小,可忽略不计.
叶柄可简化为悬臂梁,一端固定于墙壁,另一端自由且承受集中力和力矩.静态变形时,叶柄在xz平面上某点P的弯转角(叶柄切线与竖直线的夹角)ϕ(图3(b))由如下方程描述
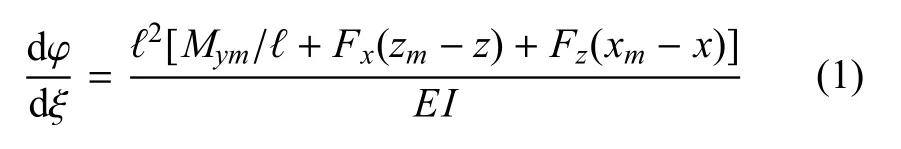
其中,ℓ为叶柄总长,ξ为叶柄上点P的无量纲曲线坐标,即P点到固定端的曲线长度占叶柄总长度的比例;x,z为P点的无量纲直角坐标值;xm,zm为叶柄末端(自由端)的无量纲直角坐标值.Fx和Fz分别为作用于叶片的气动力在x和z方向的分力.I为叶柄横截面惯性矩.E为叶柄弹性模量,其测量研究见文献[30].Mym为Fx和Fz对叶柄末端的时均力矩.实验发现,叶片在静态变形时主叶脉近似保持直线,不发生弯曲,叶柄自由端的弯转角ϕm与叶片角θ之间的关系为

根据天平3个分力和3个力矩的测量结果,可知叶片气动力的作用点接近于叶片中间长度位置,即有
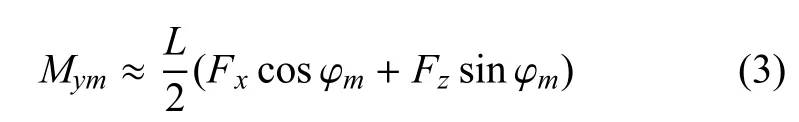
其中,L为叶片长度.将式(1)两端对ξ求导,根据x和z对ξ的导数与ϕ的关系,得到

根据测量的气动力,由式(5)可求出A1和A2,然后求解式(4)求出叶柄末端倾角ϕm,再根据式(2)求出叶片角θ.
图10为计算的不同尺寸树叶的叶片角随风速的变化.尽管个体之间有一定差异,但各叶片角的变化趋势一致:当风速很小时,叶片角接近于90°(叶片接近于竖直).随着风速增大,叶片角迅速减小.当风速达到5m/s时,各叶片角都减小了一半以上.风速进一步增大时,叶片角变化率减小.风速大于15m/s后,叶片角趋近于0°,叶片卷成堆状,主叶脉处于水平位置,阻力系数减至最低.

图10 不同树叶的叶片角随风速的变化,其中叶柄弹性模量E=600MPa,叶柄长度和直径因叶柄的不同而变化Fig.10 Change of leaf angle with wind speed,where the petiole elastic modulusE=600MPa,the petiole length and diameter vary with the di ff erence of petiole
由式(4)求出叶片弯角ϕ后,根据叶柄几何关系可得到叶柄曲线.图11为典型的叶柄曲线随风速的变化情况.当风速在0~4.86m/s之间时,叶柄弯曲变化最为迅速.风速大于4.86m/s后,叶柄弯曲变化较缓,尤其是风速在4.86~10.38m/s之间和大于15.86m/s以后,变化很小.当风速大于15.86m/s时,叶柄末端趋近于水平位置.
3 结论

图11 叶柄弯曲程度随风速的变化,其中叶柄弹性模量E=600MPa,叶柄长ℓ=0.12m,叶柄平均直径d=1.8mmFig.11 Change of a petiole bending with wind speeds,where the petiole elastic modulusE=600MPa,the petiole length ℓ=0.12m,and the averaged petiole diameterd=1.8mm
叶柄端部固支于刚性棒上,使叶柄和叶片自然垂挂于风洞中,分叶片正面迎风和反面迎风两种情况,分别进行气动测试.测试的风速范围 0~27m/s内,发现了低频左右摆动、第一和第二高频振动等3种树叶振动状态,以及飞翼和锥形两种树叶静止状态,同时找出了相应的5个临界风速.对于很多测试叶片来说,这些状态并不是全部出现,而是其中几种出现,另外几种并不出现,而且对同一片树叶,正面迎风与反面迎风时出现的状态也不尽相同.通过对70余片随机采集的树叶测试结果的统计,得到了各振动和静止状态存在的概率,以及各临界风速的期望值.叶片正面和反面迎风时各状态存在的概率和各临界风速值作了对比.烟线流动显示和PIV测量发现,不同风速下树叶尾流中均存在旋涡脱落现象;通过摄像观察知道,叶片的3种振动形式都伴随着叶柄的振动.将叶柄按照悬臂梁模型处理,将叶片气动力简化为悬臂梁末端受集中载荷和弯矩.根据测量的气动力结果计算静态变形时叶片角和叶柄弯曲形状随风速的变化,发现当风速从0升高到5m/s时,叶柄弯曲程度变化很大,再增大风速,弯曲变化趋于缓慢.
1 Ennos AR.Compliance in plants//Jenkins CHM ed.Compliant Structures in Nature and Engineering,21-40.Montana:WIT Press, 2005
2 Vogel S.The Life of A Leaf,204-225.Chicago:The University of Chicago Press,2012
3 Hadhazy A.Power plants:Artificia trees that harvest sun and wind to generate electricity.Scientifi American,2009,306(5):31-32
4 Sharif S,Gentry TR,Yen J,et al.Transformative solar panels:a multidisciplinary approach.International Journal of Architectural Computing,2013,11(2):227-245
5 Schindler D,Bauhus J,Mayer H.Wind e ff ects on trees.European Journal of Forest Research,2012,131:159-163
6 Vogel S.Drag and reconfiguratio of broad leaves in high winds.Journal of Experimental Botany,1989,40(217):941-948
7 Miller LA,Santhanakrishnan A,Jones S,et al.Reconfiguratio and the reduction of vortex-induced vibrations in broad leaves.Journal of Experimental Biology,2012,215:2716-2727
8 Speck O.Field measurements of wind speed and reconfiguratio in Arundo Donax(Poaceae)with estimates of drag forces.American Journal of Botany,2003,90(8):1253-1256
9 Schouveiler L,Boudaoud A.The rolling up of sheets in a steady fl w.Journal of Fluid Mechanics,2006,563:71-80
10 Alben S,Shelley M,Zhang J.Drag reduction through self-similar bending of a fl xible body.Nature,2002,420:479-481
11 Gosselin FP,de Langre E.Drag reduction by reconfiguratio of a poroelastic system.Journal of Fluids and Structures,2011,27(7): 1111-1123
12 Shelley MJ,Zhang J.Flapping and bending bodies interacting with flui fl ws.Annual Review of Fluid Mechanics,2011,43:449-465
13 Albayrak I,Nikora V,Miler O,et al.Flow–plant interactions at leaf, stem and shoot scales:drag,turbulence,and biomechanics.Aquatic Science,2014,76:269-294
14 Taneda S.Waving motions of flagsJournal of the Physical Society of Japan,1968,24:392-401
15 Posada JM,Lechowicz MZ,Kaoru Kitajima K.Optimal photosynthetic use of light by tropical tree rows achieved by adjustment of individual leaf angles and nitrogen content.Annals of Botany,2009,103:795-805
16 Pisek J,Ryu Y,Alikas K.Estimating leaf inclination and G-function from leveled digital camera photography in broadleaf canopies.Trees,2011,25:919-924
17 McNeil BE,Pisek J,Lepisk H,et al.Measuring leaf angle distribution in broadleaf canopies using UAVs.Agricultural and Forest Meteorology,2016,218-219:204-208
18 Hernandez LF.Leaf angle and light interception in sunfl wer(HelianthusannuusL.).Roleofthepetiole’smechanicalandanatomical properties.Phyton-International Journal of Experimental Botany, 2010,79:109-115
19 张富云,赵燕.鹅掌楸属植物研究进展.云南农业大学学报,2005,20(5):697-701
20 王沁峰,张晓平,王乐林等.二球悬铃木展叶期叶片生长及3个生理指数的动态变化.植物资源与环境学报,2009,18(2):94-96(Wang Qinfeng,Zhang Xiaoping,Wang Lelin,et al.Dynamic changes of leaf growth and three physiological indexes of Platanus acerifolia during leaf expansion stage.Journal of Plant Resources and Environment,2009,18(2):94-96(in Chinese))
21 曹利祥,袁方,石喜乐等.悬铃木早期萌芽及叶片生长的动态变化.北方园艺,2011,24:95-96
22 Niinemets U,Fleck S.Petiole mechanics,leaf inclination,morphology,and investment in support in relation to light availability in the canopy of liriodendron tulipifera.Oecologia,2012,132(1):21-33
23 Niklas KJ.A mechanical perspective on foliage leaf form and function.New Phytologist,1999,143:19-31
24 Scholes RJ,Prost PGH,Tian Y.Canopy structure in savannas along a moisture gradienton Kalahari sands.Global Change Biology, 2004,10:292-302
25 Shao CP,Chen YJ,Lin JZ.Wind induced deformation and vibration of a Platanus acerifolia leaf.Acta Mechnica Sinica,2012,28(3): 583-594
26 Tadrist L,Julio K,Saudreau M,et al.Leaf flutte by torsional galloping:Experiments and model.Journal of Fluids and Structures, 2015,56:1-10
27 Roshko A.On the wake and drag of blu ffbodies.Journal of Aeronautical Science,1955,22:124-132
28 Williamson CHK,Govardhan R.Vortex-induced vibrations.Annual Review of Fluid Mechanics,2004,36(1):413-455
29 Williamson CHK,Govardhan R.A brief review of recent results in vortex-induced vibrations.Journal of Wind Engineering and Industrial Aerodynamics,2008,96(6):713-735
30 NiklasKJ.The elasticmoduli and mechanics of Populas tremuloides (Salicaceae)petioles in bending and torsion.American Journal of Botany,1991,78(7):989-996
THE DEFORMATION AND VIBRATION OF TULIP LEAVES IN WIND1)
Shao Chuanping2)Zhu Yuanyuan
(Institute of Fluid Masurement and Simulation,China Jiliang University,Hangzhou310018,China)
The study of aerodynamic and solid-fluicoupling characteristics of tree leaves is of significanc in tree protection,new power generation technology and solar panel design.Vogel firs observed that a tree leaf could reconfigur itself at high winds to avoid damage.Vogel’s leaf was freely supported at its petiole end,which is quite di ff erent from the natural way of petiole-branch connection.In our study,the leaf was clamped at the end of its petiole.The lamina was vertically hanging,with its front or back surface facing wind.Two types of lamina steady status,i.e,wing steady and conic steady,three types of lamina vibration,i.e,low frequency sway,1st and 2nd high frequency vibration,and 5 critical wind speeds were observed in the range of wind speed 0~27m/s.The probability of existance of every status and the expected value of each critical wind speed were obtained by statistics of the results of more than 70 leaves.The phenomenon of vortex shedding from a deformed leaf was found by fl w visualization.Wind tunnel balance measurement revealed that the leaf drag coefficient decreased with the increase of laminaRe,and finall reached 0.1.A cantilevered beam model was introduced,and the measured aerodynamic force on the lamina was used to simulate the static bending curve of a petiole.Results showed that,the downstream bending increased rapidly with the increase of wind speed from 0 to 5m/s, but it slowed down from 5m/s to higher ones.
V211.74
A
10.6052/0459-1879-16-179
2016–06–30收稿,2016–12–05录用,2016–12–27网络版发表.
1)国家自然科学基金资助项目(11172286).
2)邵传平,教授,主要研究方向:流动控制,植物力学.E-mail:shaocp@cjlu.edu.cn
邵传平,朱园园.鹅掌楸树叶在风中的变形与振动.力学学报,2017,49(2):431-440
Shao Chuanping,Zhu Yuanyuan.The deformation and vibration of tulip leaves in wind.Chinese Journal of Theoretical and Applied Mechanics,2017,49(2):431-440

