高频脉冲管制冷机的蓄冷器源汇模型、流动模拟和参数优化1)

张 珍 李家春,†,2)

∗(中国科学院力学研究所流固耦合系统力学重点实验室，北京100190)

†(中国科学院大学工程科学学院，北京100049)

高频脉冲管制冷机的蓄冷器源汇模型、流动模拟和参数优化1)

张 珍∗李家春∗,†,2)

∗(中国科学院力学研究所流固耦合系统力学重点实验室，北京100190)

†(中国科学院大学工程科学学院，北京100049)

蓄冷器是脉冲管制冷机的一个关键部件，其工作性能将直接影响整机性能.针对工质在蓄冷器内交变流动的特性，提出了一个新的源/汇项模型来模拟蓄冷器内的流动与换热，同时模型也考虑了气固间的非热平衡.对于蓄冷器和换热器内的固体填料，在一些假定条件的基础上推导得到了固体物质的温度分布的解析解.该模型不需要建立固体的能量方程，减小了计算的工作量，避免了达西定律在高频下不适用的限制条件，并针对交变流动情况下对流换热系数的取值提出了解决方法.新模型的计算结果与实验结果符合良好，验证了模型的可靠性.进一步应用此模型分析了蓄冷器内部的热交换和制冷机理，并进行了蓄冷器的优化设计，对于不同目数，不同丝径，不同材料的丝网，进行了各种情况下蓄冷器的换热性能优化分析.

脉冲管制冷机，蓄冷器，源/汇项模型，对流换热系数，相位角

引言

最近几十年脉冲管制冷机经历了基本型[1]、小孔型[2]、双向进气型[3]、改进的小孔型[4]、多路旁通型[5]、惯性管型[6]、热声型[7]等一系列的变革改进后得到了飞速发展.由于空间和军事领域对脉冲管制冷机的体积和重量有苛刻要求，脉冲管制冷机的轻型化和微型化已成为关注的焦点.提高频率是减小脉冲管制冷机体积和重量的一个有效途径，因此高频脉冲管制冷机成为近几年来该领域发展的一个前沿方向.

限制高频脉冲管制冷机进一步发展的一个原因就是对高频脉冲管制冷机的机理研究仍显薄弱，尽管已有许多学者提出了各种理论来进行解释[8-11]，但对高频脉冲管制冷机内部的物理过程和工作原理的认识有待深化.

交变流动的换热特性和阻力特性是深入分析回热式制冷机工作原理以及对其进行优化的重要基础.不少学者已研究了具有不同形状填料的蓄冷器内部的交变流动和换热性能，如螺旋状盘管[12]、圆管[13]、平行板[14-16]、金属颗粒[17-19]、金属丝网[20-22].由于蓄冷器内热量和动量的传输及转换是传热学、流体力学和热力学的一个耦合过程，因此是一个相对复杂的问题.蓄冷器优化设计中固体填料的选择是一个非常重要的因素.Bejan[23]曾应用最小熵增分析法对蓄冷器进行了优化.

以往的数值模拟中蓄冷器大都采用多孔介质模型，一种是认为工质与填料温度一致，二者间无热交换的局部热平衡模型，是一种单能量方程模型[24]，这显然与实际制冷机的情况是不相符的；高凡等[25]则采用了非热平衡模型，同时计算蓄冷器内气相和固体骨架的能量方程，是一种双能量方程模型，计算较为复杂.对于高频脉冲管制冷机，工质在蓄冷器内部的丝网孔隙或换热器的板叠间流动时的雷诺数最大甚至可达100量级，达西定律不再适用，需要采用更为复杂的多孔介质模型如Darcy-Brinkman-Forchheimer模型，带有一定的半经验性质.在实验研究方面，Chen等[26-27]研发的小型台式20K低温制冷机采用了单级结构的高频脉冲管制冷机方案，单级高频脉冲管制冷机在耗功240W时，能够获得15.5K最低温度、在20K提供超过380mW制冷量. Hu等[28]在kW级大功率脉冲管低温制冷研究中采用自主研发的10kW级往复直线压缩机驱动一个结构紧凑的同轴型kW级制冷量低温脉冲管制冷机，在120K可以达到1200W以上的制冷量，在77K可以达到600W以上制冷量，该制冷机比美国的效率高出30%，是目前报道的最高效率的大功率脉冲管热声低温制冷机.

本文提出了一个新的源/汇项模型来模拟蓄冷器内的往复交变流动与换热.同时模型也考虑了气固间的非热平衡，对于蓄冷器和换热器内的固体填料，在一些假定条件的基础上得到了固体物质温度分布的解析解.该模型不需要分别建立气固各自的能量方程，减小了计算的工作量.进一步应用此模型分析了蓄冷器内部热交换和制冷机理，并进行了蓄冷器的优化设计，对于不同目数，不同丝径，不同材料的丝网，计算了各种情况下蓄冷器的换热性能优化分析.

1 动量和能量方程源汇项建模

1.1 动量方程的源汇项

丝网会对工质的流动产生阻力，导致工质的流动速度减小或驱动压力增大，通过在动量方程中增加一源项来模拟这个流动阻力.

根据前人的研究成果，得到了稳定流动条件下的经验阻力公式

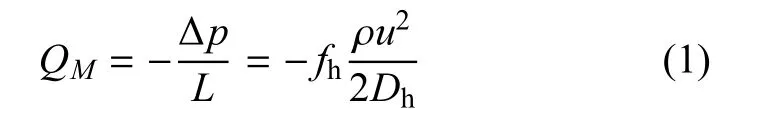
其中,∆p为蓄冷器进出口两端的压差，L为蓄冷器的特征长度，fh为蓄冷器的阻力系数，Dh为特征尺度.

对于交变流动情况下的阻力系数，Thomas等[29]已归纳总结了各种不同情况下阻力系数的取值情况

上式右边第1项为黏性阻力项，第2项为惯性阻力项.Csf,Cfd的取值见文献[29].

本文模拟采用的脉冲管制冷机系统来自于中科院理化所，该所的研究人员通过实验得到了高频交变流动情形下蓄冷器内的阻力系数的经验表达式[30]

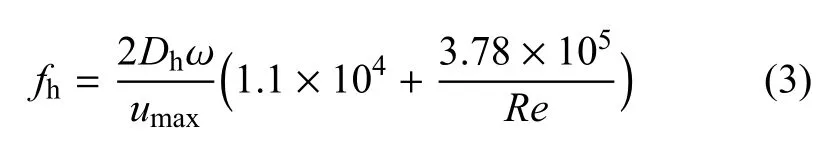
其中，ω是交变流动的频率，umax是蓄冷器内工质流动的面平均最大速度.

1.2 能量方程的源汇项

热气流通过回热器时，气体向固体填料放热；冷气流通过时，气体从填料吸热.这里采用牛顿定律来描述丝网与气体介质之间的热交换量.

其中，QE表示在单位时间、单位体积的控制体内，丝网填料与工质之间的热交换量；As为单位体积控制体内丝网的换热表面积；Ts,T分别为固体填料和工质的温度；h为对流换热系数.

图1是蓄冷器内丝网的结构示意图，可以得到单位体积内丝网的换热表面积为

其中，n是丝网的目数，Dw是丝的直径.

图1 丝网结构示意图Fig.1 Schematic diagram of wire screen

对流换热系数是一个很重要的参数，单向流动情况下对流换热系数的取值在交变流动下是不适用的，这里采用如下方法计算其取值.文献[29]给出了描述传热的无量纲参数——努塞尔特数Nu在交变流动时的取值，之后可以根据Nu的定义来求解对流换热系数

式中，u是工质的流动速度.丝网和板叠两种情况下的Nu取值是不同的，见文献[29].

1.3 固体填料的温度

对于蓄冷器内的固体丝网填料，把它假设成一系列的圆柱，圆柱的直径等于丝网的丝径，为几十微米，圆柱的长度为70mm，长径比接近1000，可假定为无限长圆柱.求解丝网填料的温度就相当于求解圆柱在与外界工质有热交换时的温度.在制冷机的工作过程中，蓄冷器内部的工质温度T在不同的轴向位置处取值是不同的，靠近冷端换热器一端的温度较低，靠近水冷器一端的温度较高.工质的温度是周期性变化且逐渐减低的，但降低的幅度很缓慢，几百个周期内工质温度才降低将近1K.因此对于缓变的气体温度，在每个周期的计算过程中，可以近似认为是一种准定常状态，在每个周期内的工质的温度可认为是常数.

求解此方程组得到了固体填料温度的解析解

其中r0为丝的半径，为系统的初始温度，λn是超越方程的根，M和N的表达式见附录.

对于水冷器，冷端换热器和热端换热器等填充有板叠的部件，固体填料可看成是一系列的平行薄板，相当于求解平板在与工质有热交换时的温度

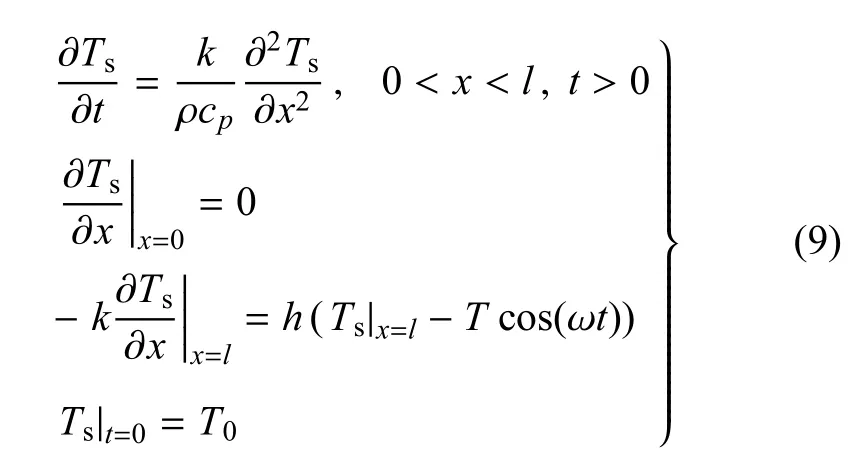
得到板叠温度的解析解为

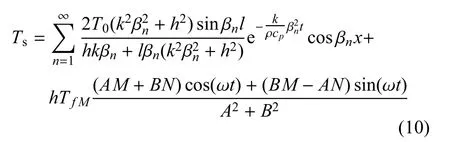
其中l为板叠厚度的一半，βn是超越方程tan(βl)=的根，A,B,M,N的表达式见附录.

传统的土木工程专业应用型本科人才培养注重宽厚的学科理论基础，偏重于基础知识和理论的传授，忽视应用能力的培养。“卓越计划”对实践教学环节的要求是“具有综合运用所学科学理论、分析和解决问题方法和技术手段分析并解决工程实际问题的能力，能够参与生产及运作系统的设计，并具有运行和维护能力”[3]。高等教育强调知识体系系统性，课程体系讲究前后承接，按照毕业生应具有的知识、能力、素质的12条要求，随着工程教育环境的变化以及企业对人才能力需求的变化，人才培养过程中工程实践能力的提高，需要得到重视。

假定蓄冷器内丝网材质为不锈钢，直径50µm,对流换热系数200W·m-2·K-1，气体温度为300K，边界条件为第3类边界条件.图2给出了蓄冷器内丝网表面的温度变化幅度(即该处温度与初始温度的差值)在不同频率下的取值情况.温度变化幅度随着频率的增大而降低.

图2 频率对丝网表面处温度幅值的影响Fig.2 E ff ect of frequency on the temperature amplitude at the surface of the wire screen

假定冷、热端换热器内板叠材质为紫铜，板叠的一半厚度为 1mm,频率 50Hz,对流换热系数200W·m-2·K-1，图3给出了板叠内的温度分布.板叠表面处的幅值最大，越靠近板叠内部温度幅度逐渐降低.

图3 板叠内各处的温度分布情况Fig.3 Temperature distribution within the inner plate stack

图4 不同材质板叠表面处的温度变化Fig.4 Temperature change at the surface of plate stack with di ff erent materials

图4给出了在板叠厚度、工作频率、对流换热系数相同的情况下，不同材质的板叠表面处的温度变化.紫铜板叠的温度幅值小于不锈钢的，且不锈钢板叠的温度整体低于紫铜的.关于蓄冷器填料的选择在第4小节讨论.

2 惯性管型脉冲管制冷机的流动模型

2.1 流动模型

研究对象是一套由中科院理化所自主开发研制的惯性管型脉冲管制冷机系统.其二维轴对称模型如图5所示，各主要部件的尺寸列于表1.本次模拟计算的部件包括水冷器、蓄冷器、冷端换热器、脉冲管和热端换热器.流动模型采用二维层流模型，工质氦气假定为理想气体.

表1 惯性管型脉冲管制冷机各部件尺寸Table 1 Dimensions of ITPTR

图5 惯性管型脉冲管制冷机系统示意图(1压缩机；2水冷器；3蓄冷器；4冷端换热器；5脉冲管；6热端换热器；7惯性管；8气库)Fig.5 Schematic diagram of ITPTR:(1)compressor,(2)water chilling heat exchanger,(3)regenerator,(4)cold end heat exchanger,(5)pulse tube,(6)hot end heat exchanger,(7)inertance tube,(8)gas reservoir

控制方程主要包括质量，动量和能量方程

其中，T,p,ρ,cp,µ,k分别表示工质的温度，压力，密度，定压比热，黏度，导热系数；V是速度矢量；t是时间;Φ是黏性耗散项.

以上控制方程适用于脉冲管.对于水冷器，蓄冷器，冷端换热器和热端换热器等部件，则采用以下控制方程

工质氦气的热物性参数如导热系数和黏度系数均认为是温度的函数[31]

2.2 边界条件

水冷器左端的线性压缩机采用压力输入边界条件

热端换热器的右端采用质量流输出边界条件

其中，Pm,Pa分别表示整个系统的操作压力和压力幅值；ma为质量流的幅值；f是频率，θ为热端换热器右端出口处的压力波与质量流之间的相位差，可以由惯性管调节.

模型中针对冷端换热器，视研究的需要而决定其壁面条件：计算制冷机能获得最低温度时采用绝热边界条件；计算某温度下制冷机能获得制冷量时采用定壁温边界条件.蓄冷器和脉冲管保持绝热边界条件，其余部件壁面保持定壁温300K.整个系统的充气压为3.0MPa，初始温度为300K.为了加速计算过程，蓄冷器和脉冲管内的工质初始温度分布假定为线性分布.

3 模型与实验结果对比

本文的数值模拟以 Fluent14.5软件为计算平台，对所建立的源/汇项模型进行了验证.计算采用的制冷机尺寸是由中科院理化所提供的(见图5，表1)[32].试验共设计了5套方案，选择了其中的两套进行了数值模拟，这两套方案的区别在于热端材质的选取不同，方案1中热端材质选用的是不锈钢，方案2选用的是紫铜.将数值模拟结果与中科院理化所的实验结果进行比较，图6为不同频率下的冷端换热器最低温度的比较.模拟结果显示方案1的结果与方案2差距比较大，试验的结果也是如此，主要原因可能是由于不锈钢材料的热导率比较小，压缩机的压缩热积聚于热端换热器部分，无法通过其热端传递出去，因此其散热效果并不太好，热端温度较高.最终选择了方案2的设计.

图6 CHX最低温度的实验结果与计算结果比较Fig.6 Comparison of the temperature of CHX between experimental and numerical results

实验室又对方案2的样机在不同频率下的最低温度进行了实验分析，也对此进行了数值模拟，如图7所示，模拟结果的趋势与试验结果的趋势一致.验证结果显示建立的源/汇项模型是切实可行的，这为后续的深入分析奠定了基础.

图7 CHX最低温度的实验结果与计算结果比较Fig.7 Comparison of the temperature of CHX between experimental and numerical results

4 蓄冷器优化分析

4.1 蓄冷器填料优化的性能指标

蓄冷器填料的选择中需遵循两个原则，一是填料要有很大的体积比热容，这将直接决定单位体积的蓄冷器可以储存的热量值.另一个是要有足够大的换热面积，保证工质与填料能够充分换热.这里引入可用热容ca的概念.可用热容表示在单位面积对应的热渗透深度区域内，温度每变化1K所吸收的或放出的热量.ca值越大表示蓄冷材料的换热能力越强.

式中，ρs,cs,ks分别为填料的密度、比热容和热导率.

回热损失率是一个表征回热器换热性能好坏的指标，文献[34]中定义的交变流动下的回热损失率为

式中，m,h是工质的质量流量和焓流量.时间区间0到τ1表示热流体流经蓄冷器的时间段，τ1到τ表示冷流体流经蓄冷器的时间段.H1表示一个周期内蓄冷器冷端的净焓，H2,H3分别表示为蓄冷器热端和冷端流入的焓值.这里以80K温区下的制冷量为研究对象，研究了丝网的目数、丝径及材质对制冷量的影响.计算所用的丝网参数见表2.

表2 回热器计算所用丝网的参数[34]Table 2 The parameters of mesh matrix for the di ff erent regenerator[34]

4.2 丝网几何尺寸的优化

图8和图9分别揭示了频率为50Hz时回热器内的丝网目数和丝径对制冷量的影响.丝网的目数越大，丝径越细，意味着流体与填料间的换热面积越大，换热越充分，制冷量越高.对同一目数的丝网来说，制冷量随着丝径的增大先增加后降低，在某一丝径下达到最大值，即存在着一个最优的丝径值.选择400目25µm的不锈钢丝网较合适的.

图8 丝网目数对制冷量的影响Fig.8 The e ff ect of mesh number on cooling capacity

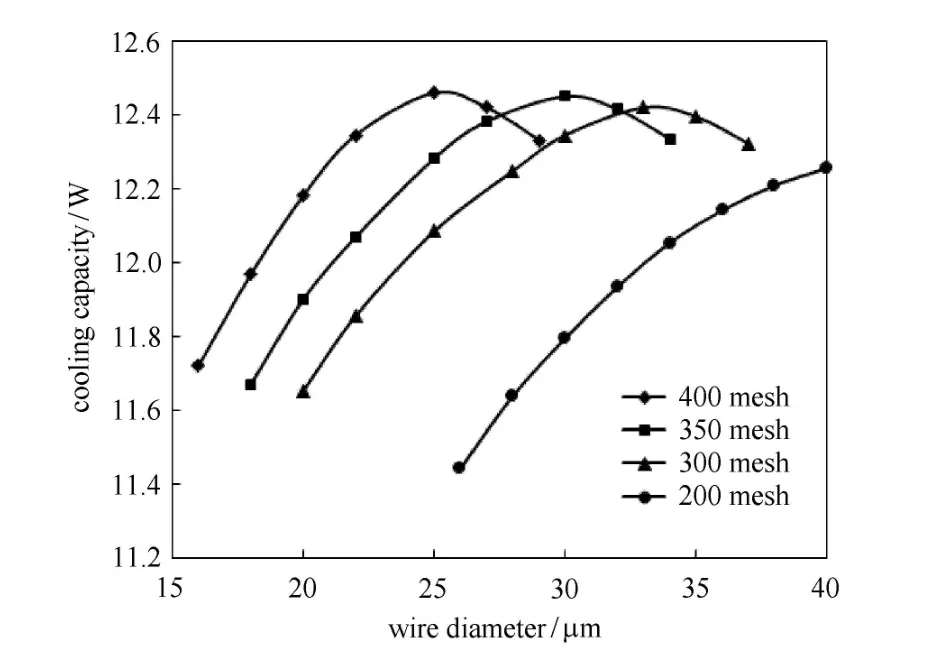
图9 丝网直径对制冷量的影响Fig.9 The e ff ect of wire diameter on cooling capacity

4.3 丝网材质的优化

表3反映了 50Hz时 400目丝网回热器中不同的比热容、密度及热导率对制冷量的影响.其中表示相对归一化后的参数，是计算中模拟采用的填料物性参数与不锈钢物性参数的比值.从表中看出:(1)填料的比热容和密度越大，意味着可用热容大，即蓄冷材料的换热能力越强，制冷量越大，如N3和N5.但N3的制冷量又略高于N5，说明比热容对制冷量的影响比密度要显著一些；(2)热导率增大，可用热容也随之增大，但制冷量却越小，如N7的热导率比N1提高了一倍，N7的可用热容比N1增大了1.4倍，但是它的制冷量却比N1下降了6%.这是由于在回热式热机中热导率大会引起严重的轴向漏热损失，回热器的漏热损失会随着热导率的增大而增加.因此回热器的填料应该选择密度和比热容较大，而热导率相对低的材料，以提高回热器的综合换热能力.

表3 不同热物性参数下的热穿透深度和制冷量Table 3 Heat penetration and cooling capacity at di ff erent thermal-physical properties

表4给出了4种不同目数、材质及运行频率的回热器的参数.图10为不同回热器的回热损失率比较.对于相同目数及运行频率的回热器，材质为铜的回热器(N8)的回热损失高于材质为不锈钢的回热器(N9).N9和N10同为不锈钢材质，N10的丝网目数大，比表面积较大，能与工质充分换热，因此回热损失较小.N11的回热损失率低于N9，说明工作频率对回热损失率也有一定的影响，随着频率的增大，回热损失率降低.文献[31]也有类似的结论，随着频率的增大回热损失率降低.文献[35]给出了10～80K温区时高频回热器的损失率在0.6%以内，计算结果在这个范围内.Nam[36]通过实验得到4.6Hz时的回热损失率为0.85%，当频率增大到60Hz时的回热损失率为0.34%，实验得到的趋势与计算结果相吻合.

表4 不同回热器的参数Table 4 Regenerator with di ff erent parameters

图10 不同回热器的回热损失率Fig.10 The regenerative loss rate with di ff erent parameters

4.4 基于热力循环分析的优化

表5显示随着频率的增大，工质微团的换热时间减小，单位质量工质的周期换热量逐渐降低.图11表明不同频率下制冷机的最低温度和蓄冷器内单位质量工质单位时间内的换热量变化趋势相反，蓄冷器内单位质量工质单位时间内传递的热量越大，制冷机的制冷温度越低.说明对于某一制冷机系统，随着工质频率的增大，单位质量工质的周期换热量降低，但是单位时间内的换热次数增加，频率与周期循环换热量乘积将出现一个最大值，出现最大值时的频率即为该制冷系统的最优运行频率，即最优运行频率是由频率和工质周期循环换热量共同作用的结果.

表5 不同频率蓄冷器内单位质量工质的周期换热量Table 5 Heat exchange per cycle of unit mass working gas under di ff erent frequencies in regenerator

图11 制冷机最低温度和蓄冷器内单位质量工质单位时间内的换热量随频率的变化Fig.11 Variations of the minimum temperature and heat transfer per unit time and mass with frequency

惯性管依靠管内气体的惯性效应产生的驻波抵消来自脉管和回热器的空体积所引起的驻波，使得部分或全部驻波从脉管的热端进入惯性管中.模型中用热端换热器右端出口处的压力波与质量流之间的相位角θ来反映惯性管的调相作用.θ值越大说明惯性效应逐步增大.图12给出了制冷量及水冷器左边进口端的压力波与质量流之间的相位角φ随热端换热器右端出口处的相位角θ的变化曲线，可以看出，制冷量与水冷器左边进口端的压力波和质量流之间相位角φ的变化趋势一致，且其中存在一个最佳的θ值(在35°左右)，此时，压力波与质量流间的相位角φ接近180°，这时压气机功率最大，对应的制冷量也最大，意味着脉冲管及回热器的空体积所产生的驻波绝大部分被惯性管的惯性效应消除了.

5 结论

(1)本文提出了一个新的源/汇项模型来模拟蓄冷器内的流动与换热，同时模型也考虑了气固间的非热平衡过程，获得了气固换热的解析解.新模型不需要建立固体的能量方程，减小了计算的工作量.同时新模型扩大了适用范围，避免了达西定律在高频下不适用的限制条件.并针对交变流动情况下对流换热系数的取值提出了解决方案.通过与实验结果的对比，验证了新模型的可靠性.

(2)应用新模型模拟典型工况，分析了蓄冷器内部的热交换和制冷机理，阐明压缩机通过驱动工质做往复交变流动将冷端换热器处的能量逐渐转移和储存到蓄冷器的丝网中的全过程，从而使提高和控制制冷剂的工作效率成为可能.

(3)以不同目数和丝径、不同材质的丝网回热器为研究对象，通过可用热容、回热损失率和运行频率等指标对回热器的换热性能进行优化分析.发现填料的比热容和密度越大，制冷量越大；采用目数大和热导率低的丝网填料时回热损失率低.最优运行频率是由频率和单位质量工质周期循环换热量共同作用的结果.

(4)惯性管的调相能力很强，尤其适用于高频脉冲管.对于某套脉冲管系统存在一个最优相位差，此时压力波与质量流间的相位角接近180°，这时压缩机的功率最大，对应的制冷量也最大.

致谢本工作得到了中科院理化所杨鲁伟课题组的支持，同时与陈燕燕博士和戴群特博士进行了几次有益讨论，谨此一并致谢.

1 Gi ff ord WE,Longsworth RC.Pulse tube refrigeration.Journal of Engineering for Industry(J Eng Ind),1964,86(3):264-268

2 MikulinEI,TarasovAA,ShrebyonockMP.Low-temperatureexpansion pulse tubes.Advances in Cryogenic Engineering(Adv Cryo Eng),1984,29:629-637

3 Zhu SW,Wu PY,Chen ZQ,et al.A single stage double inlet pulse tube refrigerator capable of reaching 42K.Cryogenics,1990, 30(Sup.):257-261

4 WangC,WuP,ChenZ.Modifie orific pulsetuberefrigeratorwithout a reservoir.Cryogenics,1994,34(1):31-36

5 Cai JH,Zhou Y,Wang JJ,et al.Experimental analysis of doubleinlet principle in pulse tube refrigerator.Cryogenics,1993,33(5): 522-525

6 Zhu SW,Zhou SL,Yoshimura N,et al.Phase shift e ff ect of the long neck tube for the pulse tube refrigerator//Proceedings of the 9th international cryocoolers conference,New Hampshire,USA,June 25-27,1997:269-278

7 Wheatley J,Hofle T,Swift GW,et al.Understanding some simple phenomena in thermoacoustics with applications to acoustical heat engines.American Journal of Physics(Am J Phys),1985,53(2): 147-162

8 Gi ff ord WE,Longsworth RC.Surface heat pumping.Advances in Cryogenic Engineering(Adv Cryo Eng),1966,11:171-181

9 Liang JT,Ravex A,Rolland P.Study on pulse tube refrigeration part 1:thermodynamic non-symmetry e ff ect.Cryogenics,1996,36(2): 87-93

10 Swift G.Thermoacoustic engines.Journal of Acoustic Society of America,1988,88:1145-1180

11 Radebaugh PS.Development and experimental test of an analysis model of the orific pulse tube refrigerator.Advances in Cryogenic Engineering,1987,33:851-859

12 Pan CZ,Zhou Y,Wang JJ.CFD study of heat transfer for oscillating fl w in helically coiled tube heat-exchanger.Computers and Chemical Engineering,2014,69:59-65

13 Chen YY,Luo EC,Dai W.Heat transfer characteristics of oscillating fl w regenerator fille with circular tubes or parallel plates.Cryogenics,2007,47:40-48

14 Jensen JB,Engelbrecht K,Bahl CRH,et al.Modeling of parallelplate regenerators with non-uniform plate distributions.Int J Heat Mass Transf,2010,53:5065-5072

15 Jensen JB,Bahl CRH,Engelbrecht K,et al.Analysis of single blow e ff ectiveness in non-uniform parallel plate regenerators.Int J Heat Mass Transf,2011,54:4746-4751

16 Kurzweg UH.Enhanced heat conduction in oscillating viscous fl ws within parallel-plate channels.J Fluid Mech,1985,156:291-300

17 Leong KC,Jin LW.Heat transfer of oscillating and steady fl ws in a channel fille with porous media.Int Comm Heat Mass Transfer, 2004,31:63-72

18 Leong KC,Jin LW.An experimental study of heat transfer in oscillating fl w through a channel fille with an aluminum foam.Int J Heat Mass Transf,2005,48:243-253

19 Ghafarian M,Mohebbi-Kalhori D,Sadegi J.Analysis Of heat transfer in oscillating fl w through a channel fille with metal foam using computational flui dynamics.Int J Therm Sci,2013,66:42-50

20 Tong LS,London AL.Heat transfer and fl w friction characteristics of woven-screen and crossed-rod matrixes.Trans ASME,1957,79: 1558-1570

21 Muralidhar K,Suzuki K.Analysis of fl w and heat transfer in a regenerator mesh using a non-Darcy thermally non-equilibrium model.Int J Heat Mass Transf,2001,44:2493-2504

22 Ravikumar KV,Matsubara Y.Experimental results of pulse tube cooler With inertance tube as phase shifter.Cryocoolers,1999,10: 291-298

23 Bejan A.Entropy Generation Minimization:The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes.CRC Press,1996

24 陈灵，张宇，魏小林等.脉冲管制冷机的整机二维数值模拟.制冷学报,2010,31(5):5-10(Chen Ling,Zhang Yu,Wei Xiaolin,et al.Two-dimensional numerical simulation of entire pulse tube refrigerator.Journal of Refrigeration,2010,31(5):5-10(in Chinese))

25 高凡，何雅玲，刘迎文.交变流动下丝网回热器中压降特性的数值分析.工程热物理学报,2008,29(4):668-670(Gao Fan,He Yaling,Liu Yingwen.Numerical analysis of pressure drop characteristic in mesh regenerator under oscillating fl w.Journal of Engineering Thermophysics,2008,29(4):668-670(in Chinese))

26 Chen LB,Jin H,Wang JJ,et al.18.6K single-stage high frequency multi-bypass coaxial pulse tube cryocooler.Cryogenics,2013,54: 54-58

27 Chen LB,Zhou Q,Jin H,et al.386mW/20K single-stage Stirlingtype pulse tube cryocooler.Cryogenics,2013,57:195-199

28 Hu JY,Zhang LM,Zhu J,et al.A high-efficiency coaxial pulse tube cryocooler with 500W cooling capacity at 80K.Cryogenics,2014, 62:7-10

29 Thomas B,Pittman,D.Update on the evaluation of di ff erent correlations for the fl w friction factor and heat transfer ofstirling engine regenerators//Proceedings of the 35th Intersociety Energy Conversion Engineering Conference and Exhibit.Las Vegas,USA,July 24-28,2000:76-84

30 Ju YL,Jiang Y,Zhou Y.Experimental study of the oscillating fl w characteristics for a regenerator in a pulse tube cryocooler.Cryogenics,1998,38(6):649-656

31 居怀明.载热质热物性计算程序及数据手册.北京：原子能出版社,1990

32 侯小锋.大冷量高频脉冲管制冷机理论与试验研究.[博士论文].北京：中国科学院理化技术研究所,2007(Hou Xiaofeng.Theoretical and experimental study of large cooling capacity high frequency pulse tube cryocoolers.[PhD Thesis].Beijing:Institute of Physics and Chemistry,CAS.2007(in Chinese))

33 Radebaugh R,Linenberger D,Voth RO.Methods for the measurement of regenerator ine ff ectiveness.NBS Special Publication,1981

34 王少恒.网格式回热器的传热特性分析与实验研究.[硕士论文].北京：华北电力大学,2012(Wang Shaoheng.Investigation and experimental research on the heat transfer characteristics of the mesh regenerator matrix.[Master Thesis].Beijing:North China Electric Power University,2012(in Chinese))

35 李卓裴，甘智华，陈杰等.液氦温区回热器高频损失特性研究.工程热物理学报,2010,31(9):1449-1452(Li Zhuopei,Gan Zhihua,Chen Jie,et al.Investigation of higrach frequency regenerator characteristics at liquid helium temperature.Journal of EngineeringThermophysics,2010,31(9):1449-1452(in Chinese))

36 Nam K,Jeong S.Measurement of cryogenic regenerator characteristics under oscillating fl w and pulsating pressure.Cryogenics,2003, 43(10-11):575-581

附录

1.圆柱与周围环境有热交换时的解析解

方程组(7)的解可分解为如下两个方程组的和

方程组(A1)的解为

M,N的表达式如下

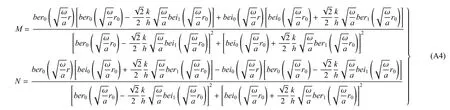
由式(A4)可知，圆柱体内温度变化的频率与外面气体温度变化的频率相同，但温度波有滞后现象，落后一个相位角φ，相位角的大小为圆柱表面处的温度幅值最大，从圆柱表面到内部温度波的振幅逐渐衰减.

方程组(A2)的解为

λn是超越方程的根.

2.板叠与周围环境有热交换时的解析解

方程组(9)的解可分解为如下两个方程组的和

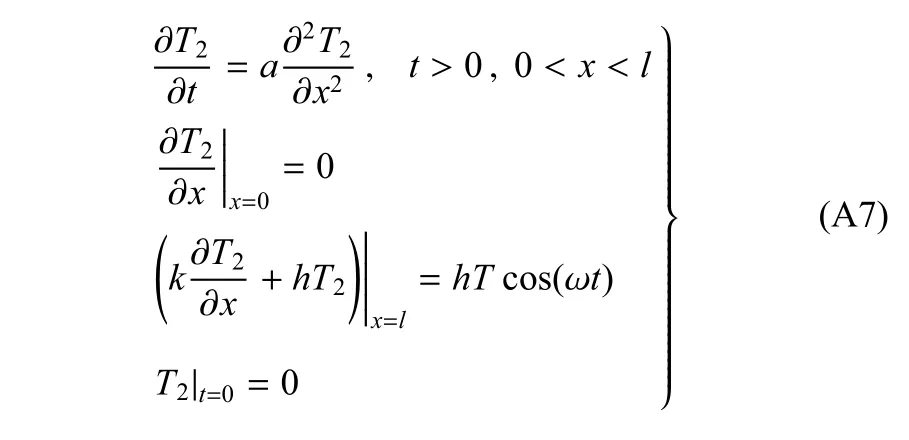
方程组(A6)的解为

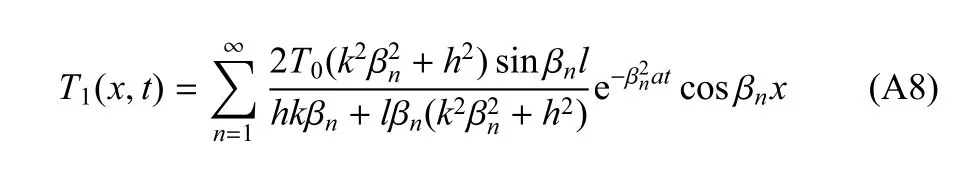
βn是超越方程的根.

方程组(A7)的解为

NEW SOURCE/SINK MODEL,FLOW SIMULATION AND PARAMETER OPTIMIZATION OF THE REGENERATOR FOR HIGH FREQUENCY PULSE TUBE REFRIGERATOR1)

Zhang Zhen∗Li Jiachun∗,†,2)

∗(Key Laboratory for Mechanics in Fluid Solid Systems，Institute of Mechanics，Chinese Academy of Sciences，Beijing100190，China)

†(School of Engineering Science，University of Chinese Academy of Sciences，Beijing100049，China)

The regenerator fille with solid matrix is one of the major components in the PTC(pulse tube cryocooler).In this paper,a new source/sink model instead of porous medium assumption,which is merely applicable for low frequency apparatus,is established to simulate the fl w and transport in the regenerator.The new model also is a non-thermal equilibrium model.Based on some assumptions,the analytic solution of the fille solid temperature can be obtained. The new model can reduce the computational workload because the model does not require the establishment of the energy equation of solid.We also propose a method to calculate the value of convective heat transfer coefficient under the alternating fl w conditions.According to the comparison with the experimental data,the new model is verified Then the model is used to analyze the heat transfer mechanism between the working fluid and the solid filler in the regenerator.The regenerator heat transfer performance are optimized under di ff erent mesh screen geometries and properties with numerical simulation.

pulse tube cryocooler(PTC)，regenerator，source/sink model，convective heat transfer coefficient，phase angle

TB61+1

A

10.6052/0459-1879-16-287

2016–10–17收稿，2017–01–06录用,2017–01–09网络版发表.

1)国家自然科学基金资助项目(50890182,11302234).

2)李家春，院士，研究员，主要研究方向：环境流体力学.E-mail:jcli05@imech.ac.cn

张珍,李家春.高频脉冲管制冷机的蓄冷器源汇模型、流动模拟和参数优化.力学学报,2017,49(2):421-430

Zhang Zhen,Li Jiachun.New source/sink model,fl w simulation and parameter optimization of the regenerator for high frequency pulse tube refrigerator.Chinese Journal of Theoretical and Applied Mechanics,2017,49(2):421-430