多储液腔航天器刚液耦合动力学与复合控制1)
岳宝增 于嘉瑞 吴文军
∗(北京理工大学宇航学院力学系,北京100081)
†(广西科技大学汽车与交通学院,广西柳州545006)
多储液腔航天器刚液耦合动力学与复合控制1)
岳宝增∗,2)于嘉瑞∗吴文军†
∗(北京理工大学宇航学院力学系,北京100081)
†(广西科技大学汽车与交通学院,广西柳州545006)
采用复合控制方法对充液航天器的姿态和轨道机动进行高精度控制.通过傅里叶--贝塞尔级数展开法,将低重力环境下液体的弯曲自由表面的动态边界条件转化为简单的微分方程,其中耦合液体晃动方程的状态向量由相对势函数的模态坐标和波高的模态坐标组成.通过广义准坐标下的拉格朗日方程得到航天器刚体部分运动和液体燃料晃动的耦合动力学方程,提出了自适应快速终端滑模策略和输入整形技术相结合的复合控制器,并分别用于控制携带有一个燃料腔和四个燃料腔航天器的轨道机动和姿态机动.通过数值模拟来验证控制器的效率和精度.结果表明,对于多储液腔航天器,如果在设计航天器的姿态和轨道控制器时没有充分考虑燃料晃动效应,那么在受控航天器系统中将会出现刚--液--控耦合问题并导致航天器姿态不稳定.而本研究中的复合自适应终端滑模控制器可以实现航天器机动的高精度控制并有效抑制液体燃料晃动.
液体晃动,多储液腔航天器,低重力环境,刚液控耦合动力学,终端自适应滑模控制器
引言
现代航天器通常需要携带大量的液体燃料和液体氧化剂[1-20].为了储存这些液体,航天器内部应携带多个储液腔[21].携带多个储液腔提高了液体晃动的第一固有频率,并且避免了液体晃动和大型柔性附件振动之间产生的共振.然而,随着储液腔的增多,系统状态变量、自由度和系数矩阵规模也随之增加,航天器系统的控制方程也将更加复杂且更难通过传统方法建立.
滑模控制是一种广为人知的航天器鲁棒控制方法.Zhu等[22]研究了具有惯性不确定性和外部干扰的航天器的姿态稳定问题,并提出了一种自适应快速终端滑模 (AFTSM)控制器.Tiwari等[23]为刚体航天器设计了一种具有全局鲁棒性和全局有限时间收敛的姿态控制器,并提出了二阶滑模控制理论.Yue等[24]基于动态反演方法和输入整形技术提出了一种用于充液航天器大角度机动的复合控制方法.虽然这些研究取得了一些成果,但其中航天器被简化为刚体,并且通过引入等效力学模型来考虑液体晃动.需要指出的是将基于等效力学模型得到的晃动动力学与航天器刚体动力学简单叠加并不能真实反映液体--航天器实际耦合系统的动力学特性[25].
本文将对由航天器主刚体和多个储液腔构成的耦合航天器系统建立数学模型,研究具有多个部分充液储液腔的航天器刚--液--控耦合动力学,设计了一种将输入整形技术与自适应快速终端滑模控制策略相结合的复合控制器,以减少液体晃动对航天器轨道和姿态机动的影响,结果表明本文所提出的控制器不仅可以确保充液航天器的位置和姿态渐近趋向目标同时还可有效抑制航天器内的燃料晃动.
1 耦合航天器系统的基本方程
1.1 航天器的物理模型与状态方程
考虑如图1所示的携带圆柱形储液腔的航天器.储液腔视为刚体,固定在航天器的主刚体上.液体视为不可压缩、无黏且无旋.正交坐标系A=B+C是惯性参考坐标系.正交坐标系A是本体坐标系,坐标轴平行于航天器的惯性主轴.其中x,y,z分别表示滚转、俯仰和偏航控制轴.滚转轴与航天器在轨飞行方向相同,俯仰轴垂直于轨道平面,偏航轴指向地球.圆柱坐标系oiriθizi和正交坐标oixiyizi的共同原点oi位于储液腔i内弯曲自由液面的中心.假设坐标系oixiyizi与坐标系oxyz平行.向量roi=[rxi,ryi,rzi]T用来表示oi在本体坐标系oxyz中的位置.未受干扰轴对称自由液面高度fi(ri)和总波高ζi(ri,θi,ti)从zi=0平面开始测量,波高ηi(ri,θi,t)从自由液面开始测量.用Wi表示储液腔i的侧壁边界条件(ri=Ri,Ri是储液腔的半径),Bi表示储液腔的底部边界条件(zi=hi,hi是储液腔中液体的高度),Si表示自由液面边界条件(zi=-ζi),Li表示自由液面和壁面接触线边界条件(ri=Ri且zi=-ζi).假设R=[Rx,Ry,Rz]T和分别代表航天器主刚体相对于坐标系OXYZ的位置矢量和姿态矢量,和分别为航天器主刚体相对于坐标系oxyz的速度矢量和角速度矢量.

图1 充液航天器模型Fig.1 Physical model for spacecraft with propellant tank
用方向余弦矩阵和欧拉角来定义航天器相对于参考系的姿态.定义欧拉角θx,θy,θz为航天器绕本体坐标系x,y,z轴的旋转角度.方便起见,定义坐标变换矩阵按照ox→oy→oz的顺序求得,因此坐标系OXYZ和坐标系oxyz之间的坐标变换矩阵为

其中,sk=sinθk,ck=cosθk(k=x,y,z).因此,可获得以下变换关系

其中ω是航天器的角速度,可认为其分量是准坐标对时间的导数.
1.2 储液腔中液体晃动方程
储液腔i中某点Pi的速度矢量为

其中vpi是点Pi相对于坐标系oxyz的位置矢量,符号()×表示相关矢量所对应的斜对称矩阵.对方程(5)引入直角坐标和圆柱坐标之间的转换关系,点Pi关于坐标系oiriθizi的速度可以写成如下形式
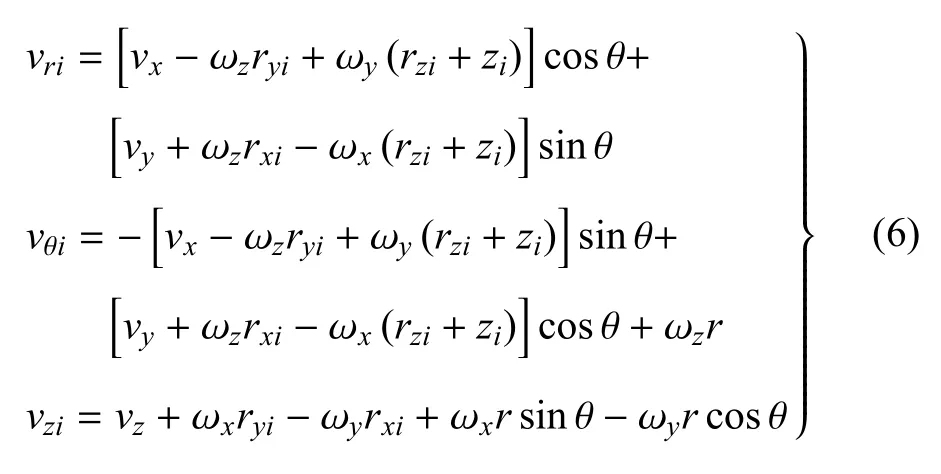
根据叠加的原理,可以将液体晃动的总速度势能函数Φ分解成扰动势函数(或相对势函数)Φr和载流子速度势Φe[2].无量纲函数Φe应满足拉普拉斯方程和储液腔侧壁和底部的非均匀边界条件
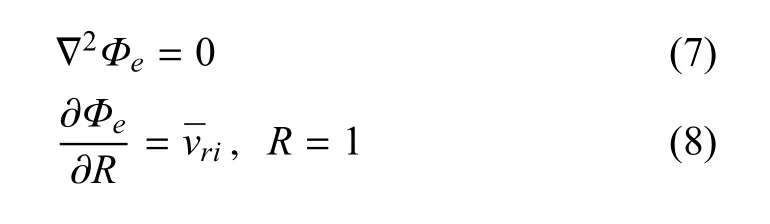
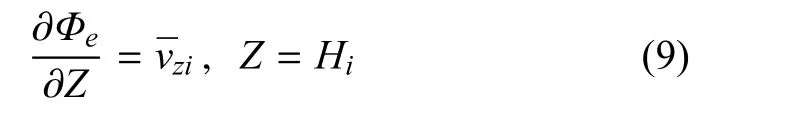

将式(10)代入式(8)和式(9),得到

方便起见,上述方程省略了θ的下标.根据式(7)、式(11)和式(12),假设函数Φe2为如下形式
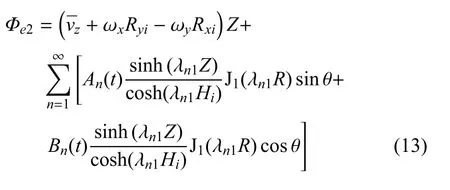
其中λn1是的根.将式(12)中的变量R用傅里叶--贝塞尔级数展开,然后与式(13)比较,展开后得到的系数An和Bn为
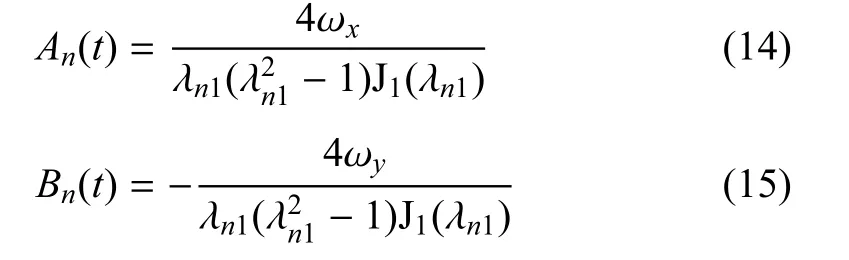
将式(14)和式(15)代入式(13),再与式(10)合并,得到势函数Φe为
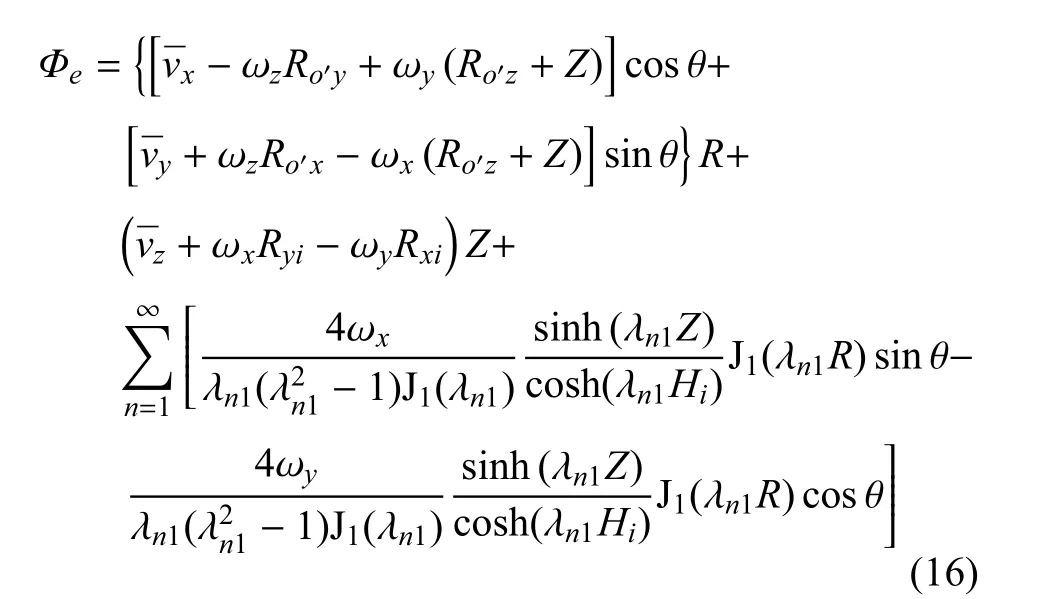
相对势函数Φr必须满足式(7)~式(9),也应该满足自由液面上的运动学和动力学条件[26]
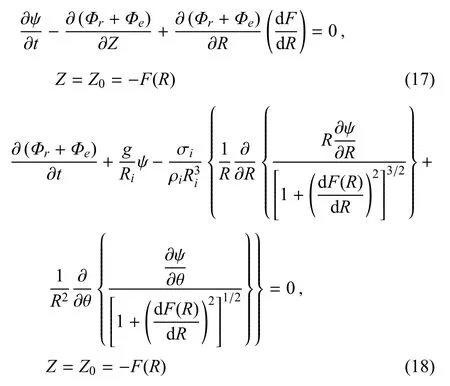
此外,无量纲波高应满足自由接触角条件,即
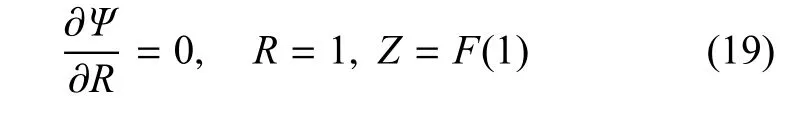
为了精确地满足式(7)和式(8),式(9)中的所有齐次边界条件,相对势函数Φr假定为
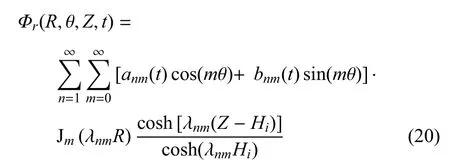
波高Ψ假定为
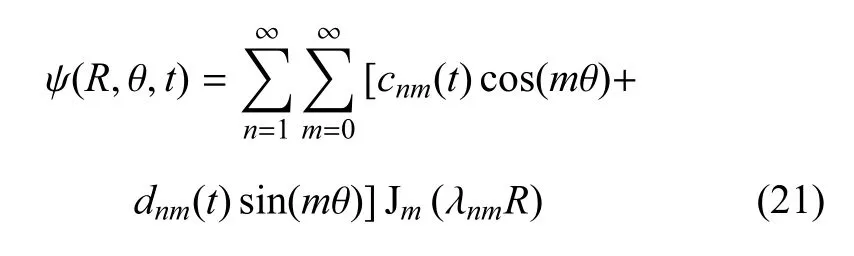
晃动力和晃动力矩是航天器稳定性和控制分析的重要晃动特性.储液腔i中的耦合晃动力属于由扰动势函数引起的扰动压力,主要包括沿着接触线作用在罐壁上的界面张力,通过图1模型推导,可以表示为


1.3 耦合系统的方程
对具有多个储液腔的航天器,运用准坐标下的拉格朗日方程来建立航天器系统的耦合方程,从而进行模块化建模[27].由储液腔中的液体晃动引起的耦合力和力矩可认为是外部非保守力和力矩,因此耦合方程组可表示为

式(27)和式(28)可以重写为

其中m0和J0分别是航天器主刚体的质量和转动惯量,f和 τ分别是控制力和控制力矩,Fi和Mi分别是储液腔i中的晃动力和晃动力矩,Ntank是储液腔的数量,v和ω分别是航天器主刚体相对于坐标轴oxyz的速度和角速度.式 (29)和式 (30)都是耦合方程.如果定义Z作为系统的状态向量,并且Z=[Rx,Ry,Rz,θx,θy,θz,vx,vy,vz,ωx,ωy,ωz]T.
2 耦合系统控制方案设计
2.1 航天器位置和姿态的自适应快速终端滑模控制方案
对于考虑惯性不确定性和外部干扰的航天器的姿态控制,这里直接给出自适应快速终端滑模(AFTSM)控制器为[22]

对于航天器的轨道控制,这里给出航天器轨道的终端滑动面
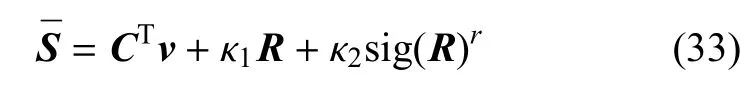
其中κ1>0,κ2>0,0<r<1.
根据参考文献[22],自适应滑模控制器中的轨道控制器可以推导为
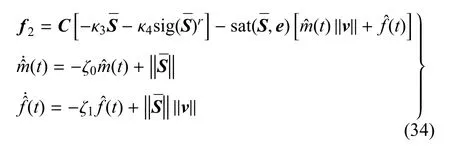
其中e=[e1,e2,e3]表示振动边界,符号函数被定义为
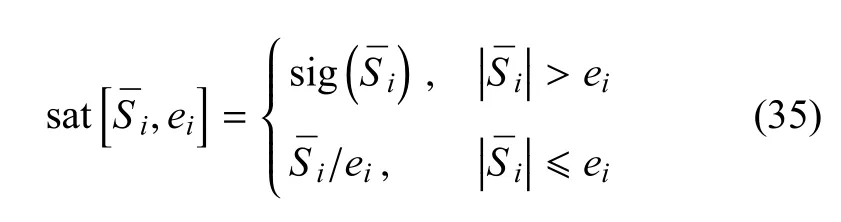
2.2 输入整形技术
输入整形技术采用前馈控制策略.因为不需要传感器反馈,前馈控制策略具有简单和有效的优点[28-29].为了增加输入整形过程的鲁棒性,Singhose[30]对整形器施加了一个使系统响应对频率的导数为零的约束,称为零振动零导数(ZVD)输入整形器.其包含如下3个脉冲
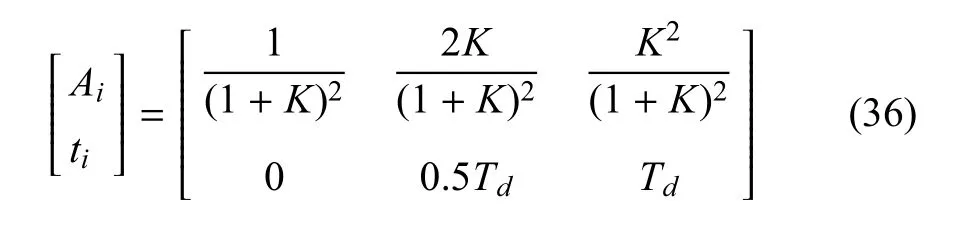
其中Ai和ti分别是脉冲i的幅值和施加时间.并且

其中ξ是阻尼比,ω0是无阻尼系统的固有频率.本文提出了一种混合控制方法,通过将输入整形技术整合到自适应滑模控制方法中,来减弱充液航天器轨道和姿态机动过程中液体晃动的动力学效应.
3 数值模拟
分别考虑携带有一个和四个部分充液的储液腔的航天器来说明本文所设计控制器的有效性,分别如图2和图3所示.假设R1=0.3m,d1=0.5m,d2=0.2m,R2=0.18m并且不同储液腔中的液体深度相同.在两种情况下,航天器内液体的总质量相同,都为m1=180kg.航天器主刚体的参数选择为:m0=200kg,Jx=400kg·m2,Jy=300kg·m2,Jz=300kg·m2.假设航天器初始姿态θ=[π/12,π/12, -π/36]T,目标位置R(0)=[10,2,3]Tm.
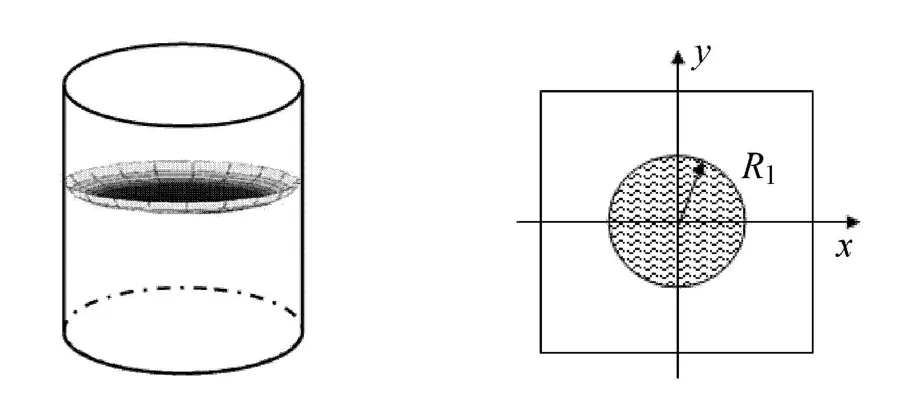
图2 单个储液腔的模型图Fig.2 Model illustration for single propellant tank
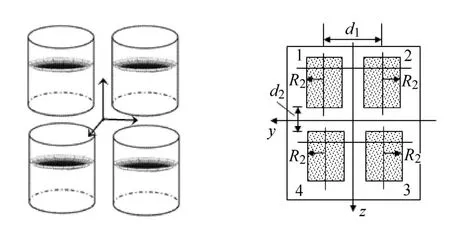
图3 4个储液腔的模型图Fig.3 Model illustration for the four propellant tanks
在数值模拟中,控制器参数的初始值选择如下:k1=0.2,k2=0.01,p=0.6,σ=0.06J0,ζ=0,Td=6.35433s.模拟结果如图4~图6所示.
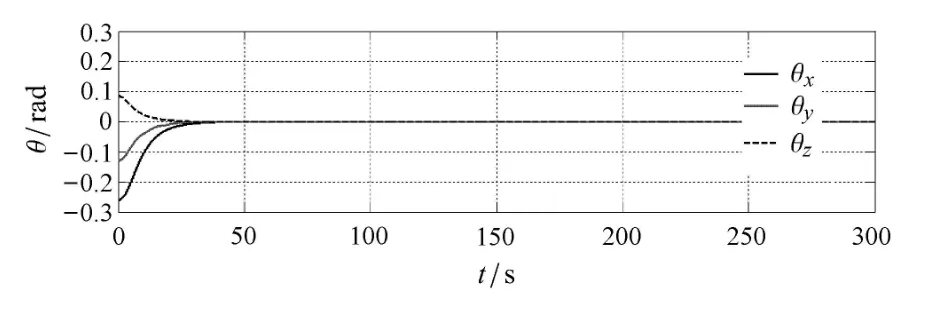
图4 欧拉角随时间的变化(单储液腔)Fig.4 Time histories of Euler angles(one tank case)
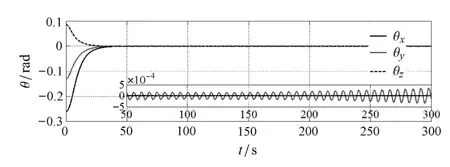
图5 欧拉角随时间的变化(四储液腔)Fig.5 Time histories of Euler angles(four tanks case)
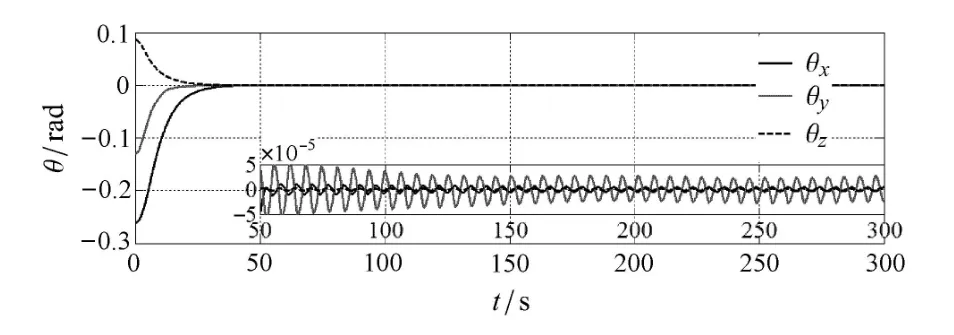
图6 使用输入整形技术后欧拉角随时间的变化(四储液腔)Fig.6 Time histories of Euler angles after input shaping (four tanks case)
数值模拟表明,文中自适应快速终端滑模控制器能很好地控制航天器的位置.如图4所示,在航天器只携带一个储液腔的情况下,使用自适应快速终端滑模控制器可以很好地控制航天器的姿态使其满足预期要求,并且精度较高.如图5所示,在航天器携带四个储液腔的情况下,航天器俯仰自旋和液体晃动之间的耦合导致持续不断的俯仰运动.图6表明,对自适应快速终端滑模控制器引入ZVD输入整形技术后,刚--液--控耦合问题已被有效地抑制,并且证明本文提出的结合输入整形技术的自适应快速终端滑模控制器的效率和可行性.对于多储液腔航天器,储液腔布局不同必然会对控制器的控制效果产生影响.通过对比,可以认为对于其他储液腔布局的航天器,自适应快速终端滑模控制器结合输入整形技术也可以改进控制效果.
4 结论和注释
本文设计了自适应快速终端滑模策略和输入整形技术相结合的复合控制器来控制航天器轨道和姿态机动.数值模拟结果表明,如果在设计携带多个储液腔航天器的姿态和轨道控制器时没有充分考虑液体晃动效应,则有可能诱导刚--液--控耦合问题并且导致航天器姿态不稳定.本文提出的输入整形自适应快速终端滑模控制器可以有效抑制多充液腔航天器耦合系统中的俯仰残余振动现象.
1 Dodge FT.The new dynamic behavior of liquids in moving containers.NASA SP-106,Southwest Research Institute,San Antonio,TX, 2000
2 Ibrahim RA.Liquid Sloshing Dynamics:Theory and Applications. Cambridge:Cambridge University Press,2005
3 Abramson HN.Dynamics of contained liquids:a personal odyssey.Applied Mechanics Review,2003,56(1):R1
4 Bang H,Lee JS,Eun YJ.Nonlinear attitude control for a rigid spacecraft by feedback linearization.KSME International Journal, 2004(18):203-210
5 Jin E,Sun Z.Robust controllers design with finit time convergence for rigid spacecraft attitude tracking control.Aerospace Science and Technology,2008(12):324-330
6 Du H,Li S.Finite-time attitude stabilization for a spacecraft using homogeneousmethod.JournalofGuidance,ControlandDynamics, 2012,35(3):740-749
7 Zhu L,Yue B.Adaptive nonlinear dynamic inversion control for spacecraft attitude fille with fuel.Journal of Dynamics and Control,2011,9(4):321-325
8 Yang D,Yue B,Zhu L,et al.Analytical method of solving the small amplitude sloshing eigenfrequencies of liquid in cassini tanks.Transactions of Beijing Institute of Technology,2011,31(11):1273-1277
9 Sidi MJ.Spacecraft Dynamics and Control.Cambridge:Cambridge University Press,1997
10 Yue BZ,Yan Y.Stability analysis of rigid-liquid-fl xible coupling dynamics ofspacecraftsystemsbyusingtheenergy-casimirmethod.Acta Scientiarum Naturalium Universitatis Pekinensis,2016,04:1-11
11 Deng ML,Yue BZ,Huang H.Study on the equivalent mechanical model for large amplitude slosh.Journal of Astronautics,2016,6: 631-638
12 Song X,Yue BZ,Yan Y,et al.Hybrid control for attitude maneuver of liquid-fille spacecraft with multiple modal liquid sloshing.Journal of Astronautics,2015,7:819-825
13 Wu WJ,Yue BZ,Huang H.Study on the rigid-liquid coupled dynamics for spacecraft with multiple partially liquid-fille cylindrical tanks.Journal of Astronautics,2015,6:648-660
14 Yue BZ,Wu WJ,Yan Y.Modeling and coupling dynamics of the spacecraft with multiple propellant tanks.AIAA Journal,2016, 54(11):1-11
15 Wu WJ,Yue BZ.Low-gravity liquid sloshing in cylindrical tanks under pitching excitation.Chinese Journal of Theoretical and Applied Mechanics,2014,2:284-290
16 Yue B,Yang D,Wu W.Nonlinear coupled dynamics of liquid-fillecylindricalcontainerinmicrogravity.JournalofDynamicsandControl,2013,11(4):306-313
17 Yang D,Yue BZ.Research on sloshing in axisymmetrical containers under low gravity.Journal of Astronautics,2013,34(7):917-925
18 Yang D,Yue BZ.Bifurcations of liquid sloshing in cylindrical containers in microgravity condition.Mechanics in Engineering,2013, 35(2):29-34,28
19 YueBZ,SongXJ.Advancesinrigid-fl xible-liquid-controlcoupling dynamics of spacecraft.Advances in Mechanics,2013,43(1):163-173
20 Yue BZ,Yu D.Research on liquid sloshing characteristics in cassini container in micro-gravity environment.Journal of Dynamics and Control,2012,10(1):76-80
21 Santo AG,Gold RE,Jr MN,et al.The MES-SENGER mission to Mercury:spacecraft and mission design.Planetary and Space Science,2001,49(14-15):1481-1500
22 Zhu Z,Xia Y,Fu M.Attitude stabilization of rigid spacecraft with finite-tim convergence.International Journal of Robust and Nonlinear Control,2011,21:686-702
23 Tiwari PM,Janardhanan S,Nabi MU.Rigid spacecraft attitude control using adaptive integral second order sliding mode.AerospaceScience and Technology,2015,42:50-57
24 Yue BZ,Zhu L.Hybrid control of liquid-fille spacecraft maneuvers by dynamic inversion and input shaping.AIAA Journal,2014,52: 618-626
25 Peterson LD,Crawley EF,Hansman RJ.Nonlinear flui slosh coupled to the dynamics of a spacecraft.AIAA Journal,1988,27:1230-1240
26 Dodge FT,Garza LR.Experimental and theoretical studies of liquid sloshing at simulated low gravity.Journal of Applied Mechanics, 1967,34:555-562
27 Meirovitch L.Methods of Analytical Dynamics. New York: McGraw-Hill,1970
28 Singer N,Seering W.Preshaping command inputs to reduce system vibration.JournalofDynamicsSystems,Measurement,andControl, 1990,112:76-82
29 Singhose W,Seering W,Singer N.Residual vibration reduction using vector diagrams to generate shaped inputs.Journal of Mechanical Design,1994,116:654-659
30 Singhose W.Command shaping for fl xible systems:a review of the firs 50 years.International Journal of Precision Engineering and Manufacturing,2009,10:153-160
RIGID AND LIQUID COUPLING DYNAMICS AND HYBRID CONTROL OF SPACECRAFT WITH MULTIPLE PROPELLANT TANKS1)
Yue Baozeng∗,2)Yu Jiarui∗Wu Wenjun†
∗(Department of Mechanics,School of Aerospace Engineering,Beijing Institute of Technology,Beijing100081,China)
†(Department of Automotive Engineering,Guangxi University of Science and Technology,Liuzhou545006,Guangxi,China)
The compound control methods are widely used to control the orbit translation and attitude maneuver of liquidfille spacecraft with high accuracy.The dynamic boundary conditions on curved liquid free surface under low-gravity environment are transformed to general simple di ff erential equations by using Fourier-Bessel series expansion method and the state vectors of coupled liquid sloshing equations are composed by the modal coordinates of relative potential function and the modal coordinates of wave height.The coupled dynamic equations for the rigid platform motion and liquid fuel sloshing are obtained by means of Lagrange equations in terms of general quasi-coordinates.The expressions of the sloshing forces and moments are obtained by analyzing the liquid model.An adaptive fast terminal sliding mode controller and a composite controller that combines the adaptive fast terminal sliding mode strategy and the input shaping technology are respectively designed to control spacecraft orbit translation and attitude maneuver for two cases.In the firs case,the spacecraft carries one partially liquid-fille propellant tank.In the second,the spacecraft carries fourpartially liquid-fille propellant tanks.The efficiency and the accuracy of the controllers are examined through numerical simulations.The results indicate that liquid-control-spacecraft coupled resonance can appear in the controlled spacecraft system if the sloshing e ff ects have not been sufficiently taken accounted of during designing attitude and orbit controller for spacecraft with multiple propellant tanks,and this resonance will result in the instability of the spacecraft attitude. Nevertheless,such disadvantages have been efficiently inhibited by using presented composite adaptive terminal sliding mode controller.
liquid sloshing,multiple propellant tanks,low-gravity environment,rigid-liquid-control coupled dynamics, adaptive terminal sliding mode controller
V448
A
10.6052/0459-1879-16-342
2016–11–24收稿,2017–01–21录用,2017–01–23网络版发表.
1)国家自然科学基金(11472041,11532002)、中国高等教育的博士点基金(20131101110002)及广西自然科学基金(2015GXNSFBA139013)资助项目.
2)岳宝增,教授,主要研究方向:非线性动力学与控制.E-mail:bzyue@bit.edu.cn
岳宝增,于嘉瑞,吴文军.多储液腔航天器刚液耦合动力学与复合控制.力学学报,2017,49(2):390-396
Yue Baozeng,Yu Jiarui,Wu Wenjun.Rigid and liquid coupling dynamics and hybrid control of spacecraft with multiple propellant tanks.Chinese Journal of Theoretical and Applied Mechanics,2017,49(2):390-396

