功能梯度材料微梁的热弹性阻尼研究1)

许 新 李世荣

(扬州大学建筑科学与工程学院，江苏扬州225127)

功能梯度材料微梁的热弹性阻尼研究1)

许 新 李世荣2)

(扬州大学建筑科学与工程学院，江苏扬州225127)

基于Euler-Bernoulli梁理论和单向耦合的热传导理论，研究了功能梯度材料(functionally graded material, FGM)微梁的热弹性阻尼(thermoelastic damping,TED).假设矩形截面微梁的材料性质沿厚度方向按幂函数连续变化，忽略了温度梯度在轴向的变化，建立了单向耦合的变系数一维热传导方程.热力耦合的横向自由振动微分方程由经典梁理论获得.采用分层均匀化方法将变系数的热传导方程简化为一系列在各分层内定义的常系数微分方程，利用上下表面的绝热边界条件和界面处的连续性条件获得了微梁温度场的分层解析解.将温度场代入微梁的运动方程，获得了包含热弹性阻尼的复频率，进而求得了代表热弹性阻尼的逆品质因子.在给定金属--陶瓷功能梯度材料后，通过数值计算结果定量分析了材料梯度指数、频率阶数、几何尺寸以及边界条件对TED的影响.结果表明：(1)若梁长固定不变，梁厚度小于某个数值时，改变陶瓷材料体积分数可以使得TED取得最小值；(2)固有频率阶数对TED的最大值没有影响，但是频率阶数越高对应的临界厚度越小；(3)不同的边界条件对应的TED的最大值相同，但是随着支座约束刚度增大对应的临界厚度减小；(4)TED的最大值和对应的临界厚度随着金属组分的增大而增大.

功能梯度材料，微梁，热弹性阻尼，能量耗散，自由振动

引言

微机电系统是在微电子技术(半导体制造技术)基础上发展起来的高科技电子机械器件.它具有许多传统结构无法比拟的优点，因此在航空、航天、汽车、生物医学、环境监控和军事等领域都有着十分广阔的应用前景[1-8].很多微机电系统谐振器可以简化为微尺度的梁[1-14].为了设计和制造高品质的谐振器就需要最大限度地降低它的能量耗散.谐振器在振动过程中主要存在两种能量耗散形式[4]：(1)外部能量耗散,空气阻尼，支撑阻尼等.(2)内部能量耗散,热弹性阻尼，声子透射、散射和晶格缺陷等.通常，当系统在完美外部坏境和支撑条件下运行时，外部能量耗散可以降到最小，此时热弹性阻尼就成为最主要的能量耗散方式.当微梁振动时，若上部受拉则下部受压，受拉区和受压区随时间交替进行，受拉区的温度会降低，受压区的温度会升高，这种温度差异会导致弹性体中的热梯度效应，且这种热梯度会通过热对流实现自调节热平衡[1,6].应变场与温度场之间存在的相互耦合给热弹性系统提供了一种能量耗散机制，使得系统回到了平衡状态.但是，在自调节热平衡过程中，热弹性体的松弛是通过不可逆的热流来实现的，从而导致了熵的耗散.这种能量耗散的过程，就称作热弹性阻尼[6].只要材料的热膨胀系数不为零，热弹性阻尼就会存在.

早在20世纪30年代，Zener首次提出热弹性阻尼理论并给出了热弹性阻尼的计算式[15-16].热弹性阻尼主要有两种表示形式，一种用热能量方法表示[1-4,9-11]，另一种用复频率方法表示[5-8,12-14].用复频率方法表示时，为了得到热弹性阻尼的大小需要求解耦合的运动方程和热传导方程，而直接求解三维的热传导方程很困难，所以很多学者将热传导方程简化为只考虑厚度方向温度梯度的一维热传导方程[5-8,12-14].对于横向振动而言，厚度方向的温度梯度比长度和宽度方向的温度梯度要大的多.也有少数学者考虑了长度或宽度方向的温度梯度,采用二维[11]或三维[7]热传导方程进行计算.他们采用了不同的解析和数值方法对均匀材料[2-8,10-14]和层合复合材料[1,9]的热弹性阻尼进行了研究.例如，非线性正则模态方法和伽辽金法[3]、拉普拉斯变换法[6]、格林函数法[1,11]等.随着微机电系统技术的快速发展对高品质低能耗的谐振器的需求，人们已开展了关于功能梯度材料微梁器件的静动态力学行为的研究[17-25].然而，关于功能梯度材料微梁谐振器热弹性阻尼的研究仍然鲜见.本文基于Euler-Bernoulli梁的理论和非均匀材料的热力耦合热传导理论研究FGM微梁谐振器的热弹性阻尼特性，探索通过材料性质在梁高度方向的梯度变化来提高和改善谐振器品质因子的可行性.文章的第1节推导了FGM微梁的运动方程和热传导方程；第2节采用分层均匀化方法建立了变系数热传导方程的递推求解数值计算过程，并利用复频率法给出了热弹性阻尼的计算公式；第3节给出了由陶瓷(Si3N4)和金属(Ni)复合而成的FGM微梁的热弹性阻尼数值解，分析了组分材料的体积分数、振动频率阶数、几何尺寸以及边界条件对其热弹性阻尼的影响规律；第4节为结论.

1 问题的数学模型

1.1 FGM微梁的材料性质

考虑矩形截面的功能梯度材料微梁，如图1所示.梁长为l，宽度为b，厚度为h.选取直角坐标系(x,y,z)，其中x与梁的轴线重合；z为横向坐标，原点在几何中面；y轴沿着梁的宽度方向.为不失一般性，假设FGM微梁由陶瓷和金属复合而成.材料成分由下表面的纯陶瓷连续变化到上表面的纯金属.并假设材料性质沿厚度按下列函数变化

式中，P(z)为材料性质参数，如弹性模量E(z)、泊松比ν(z)、质量密度ρ(z)、热传导系数κ(z)、比热容C(z)和热膨胀系数α(z)等；ψP(z)为给定的连续函数，且有ψP(h/2)=1，ψP(-h/2)=Pc/Pm；Pc和Pm分别为陶瓷和金属的材料性质.

图1 FGM微梁的几何尺寸和坐标系Fig.1 Geometry and coordinates of an FGM micro-beam

1.2 运动方程

基于Euler-Bernoulli梁理论，梁的位移场为

其中，u0(x,t)和w0(x,t)分别为几何中面上任意一点的轴向和横向位移，t为时间变量.由此可得轴向应变

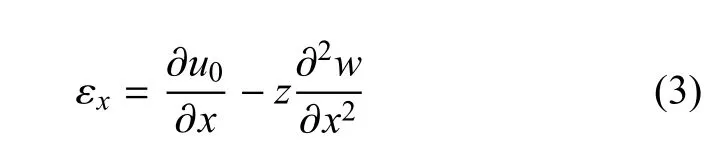
由胡克定律得到轴向应力

其中，θ(x,z,t)=T(x,z,t)-T0为微尺度梁在振动过程中因热弹性耦合而产生的温度场的增加.T为瞬态温度场，T0为参考温度(或平衡温度场).将式(3)代入式(4)可得横截面内的等效内力和弯矩

其中，Si(i=0,1,2)分别为拉伸、拉弯耦合和弯曲刚度系数，NT和MT分别为热轴力和热弯矩.这些量的具体定义为

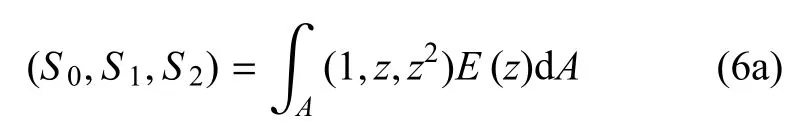
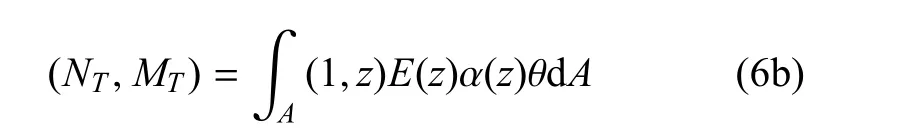
忽略轴向惯性力，可得FGM微梁的自由振动运动方程

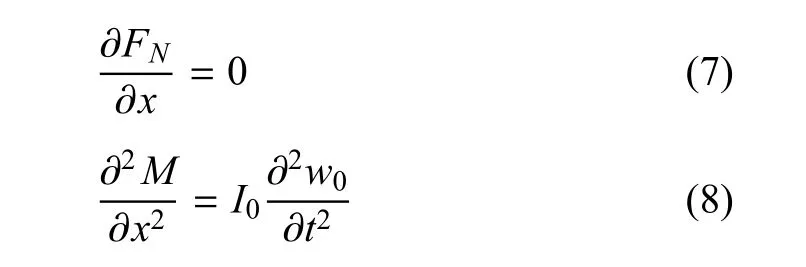
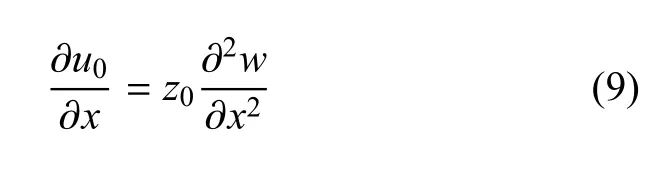
其中z0=S1/S0为梁的物理中面的坐标.对于均匀材料或材料性质分布关于梁几何中面对称的情况，不存在拉弯耦合变形，则有z0=0，表明物理中面与几何中面重合.将式(9)代入式(3)可得

进一步可得横向正应变

将式(5b)代入运动方程(8)，利用式(9)可得位移形式的运动方程

1.3 热传导方程

考虑热--弹单向耦合情况下FGM微梁单向耦合热传导方程为

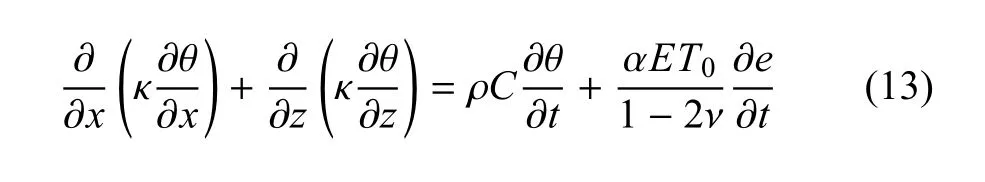
其中，e=εx+εy+εz为体积应变.对于细长梁，沿着梁厚度方向的温度梯度要远大于长度方向的温度梯度，因此，可忽略温度梯度的轴向变化，将式(10)～式(11)代入式(13)得到FGM微梁单向耦合的一维热传导方程

2 热弹性阻尼的求解

位移和温度的调和响应形式为

将式(15)代入到式(12)和式(14)得

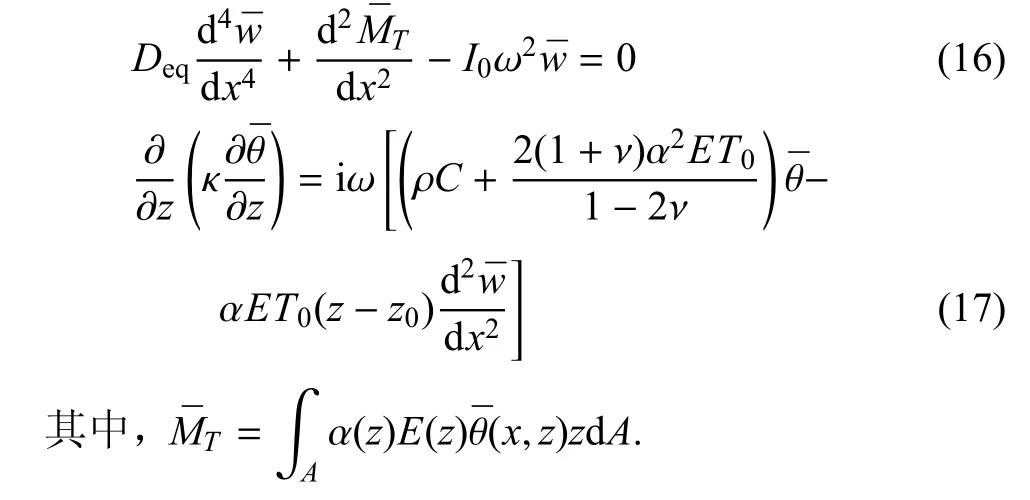
由于材料性质参数κ,ρ,C,α,E,ν都是坐标z的函数，直接求热传导方程(17)的解析解十分困难.这里采用分层均匀化方法寻求其近似解.为此，将FGM微梁沿厚度平均划分为N层子区域，将每层的材料性质看作是均匀的，并用每层的中面上的值代替.于是可得一系列常系数的微分方程

整梁的上下表面没有热流通过的，其绝热条件和界面处的连续性条件可表示为

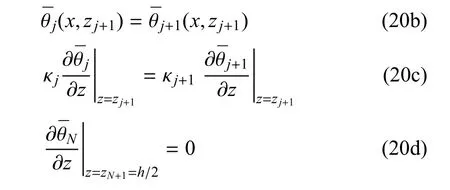
这里，j=1,2,···,N-1.

引入下列无量纲参数

带有下标“m”的物理参数代表上表面为纯金属的物理性质参数.将式(21)代入式(16)和式(19)可得无量纲形式的微分方程

系数Aj和Bj为任意常数，由边界条件和连续性条件确定.利用式(21)可将边界条件和连续性条件式(20)转化为下列无量纲形式

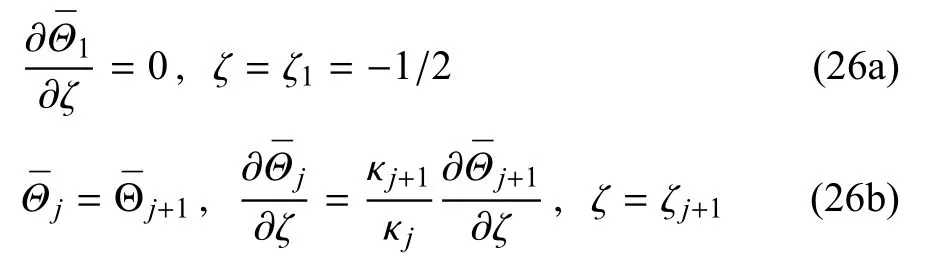
这里，j=1,2,···,N.将通解式(25)代入式(26)，即可确定系数Aj和Bj.由通解中的齐次方程特解的形式可知，系数Aj和Bj都含有项，进而可将Aj和Bj表示为

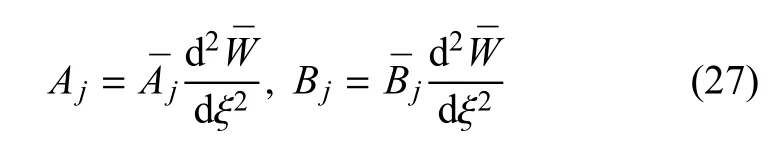
将式(25)重写

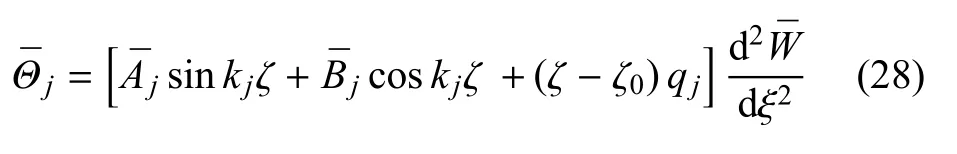
将式(28)代入边界条件和连续性条件(26)可得2N个关于系数的代数方程组.利用这组代数方程组的系数矩阵的带状特点可以容易建立递推求解的计算过程.求得温度场(28)后可得无量纲热弯矩

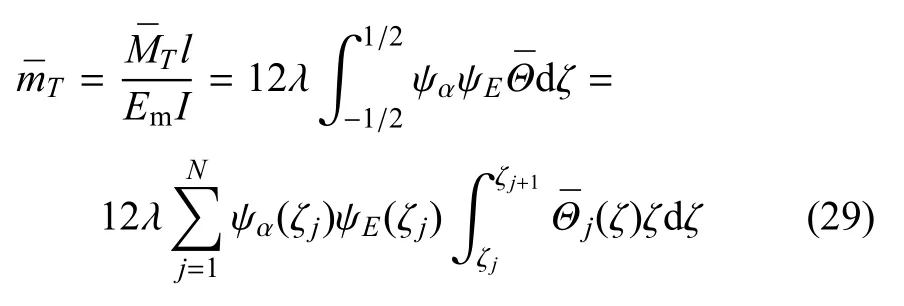
将式(28)代入式(29)得

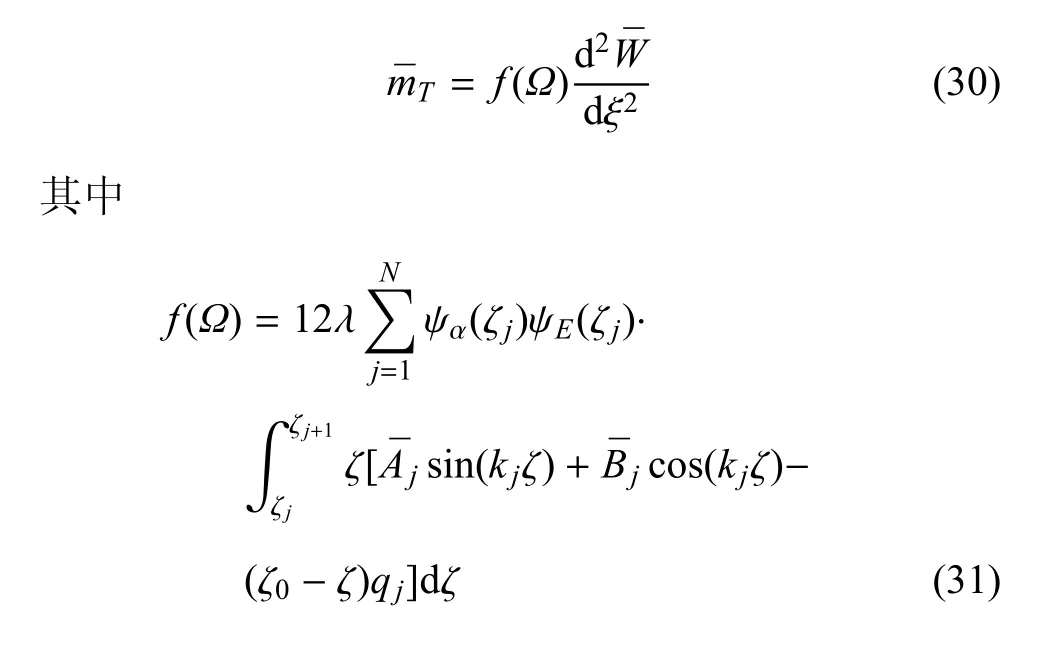
将式(30)代入式(22)得到无量纲振动方程

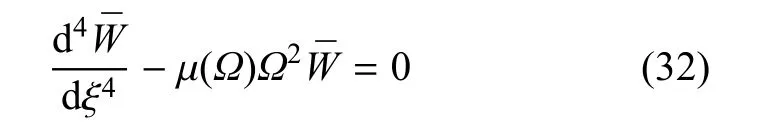
其中

如果忽略热弹性阻尼，即f(Ω)=0，则方程(32)退化为

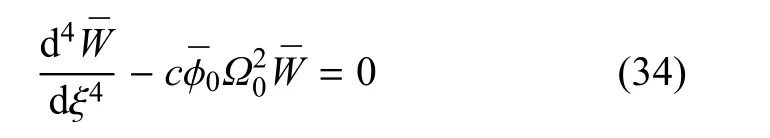
Ω0为不考虑热弹性阻尼时FGM梁的无量纲固有频率.在相同的端部支承条件下，由方程(32)和方程(34)的相似性可得到两者频率之间的关系

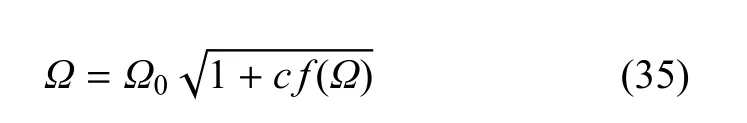
为了简化计算，用f(Ω0)近似代替根号里的f(Ω)[5].式(35)变为显式

进一步，无阻尼时功能梯度材料Euler-Bernoulli梁的频率可表示为其中为参考均匀梁(纯金属梁)的无量纲固有频率[26].从上式中可得到频率Ω的实部和虚部，进而可由下式得到代表热弹性阻尼的逆品质因子[5]

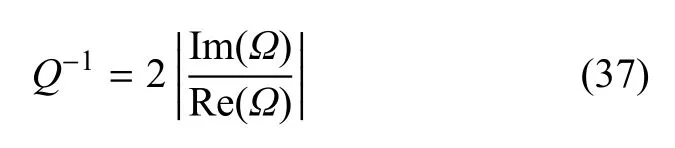
3 数值结果与讨论

考虑FGM微梁具体是由陶瓷氮化硅(Si3N4)和金属镍(Ni)复合而成，材料性质沿厚度方程按下列幂函数连续变化

其中，ζ=z/h，rP=Pc/Pm，n为材料梯度指数，取值范围为[0,∞).表1给出了镍(Ni)和氮化硅(Si3N4)的物性参数.

表1 镍和氮化硅的物性参数(T0=300K)Table 1 The material properties of nickel and silicon nitride(T0=300K)

将式(38)代入式(24)中得到无量纲系数

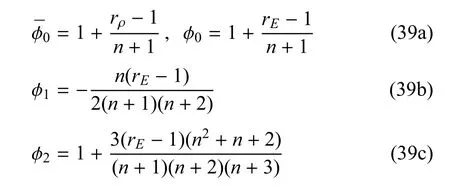
首先，考虑分层数N对热弹性阻尼精度和收敛性的影响.给定两端简支(S-S)，l=300µm，h=3µm的FGM微梁.参考均匀梁的前三阶的无量纲频率分别为π2，4π2，9π2.表2给出了当材料梯度指数n=1时，FGM微梁以一阶模态振动时不同分层数N对应的Q-1值.从表中可以看出，分层数分别为N=200和N=1000时，所得Q-1的相对误差小于2×10-5，由此可见分层均匀法具有很好的收敛速度.后续计算时取N=600已能达到了很高的精度.这是由于在求解系数的代数方程组时采用了递推求解过程，建立了类似追赶法的解析运算过程，避免了矩阵运算，使得计算过程简单而高效.为了进一步证明该计算方法的可靠性，将FGM微梁退化为纯陶瓷均匀梁(n=0)时，在N=600时计算得到的逆品质因子值与文献中的解析解[5](以下简称L-R)进行了比较(见图2).文献中L-R给出的热弹性阻尼解析公式为

表2 一阶频率下FGM微梁不同N对应的Q-1值(S-S,h=3µm,l=300µm,n=1)Table 2 Values of the quality factorQ-1with numbers of the divided layer of an FGM beam at the firs order frequency (S-S,h=3µm,l=300µm,n=1)

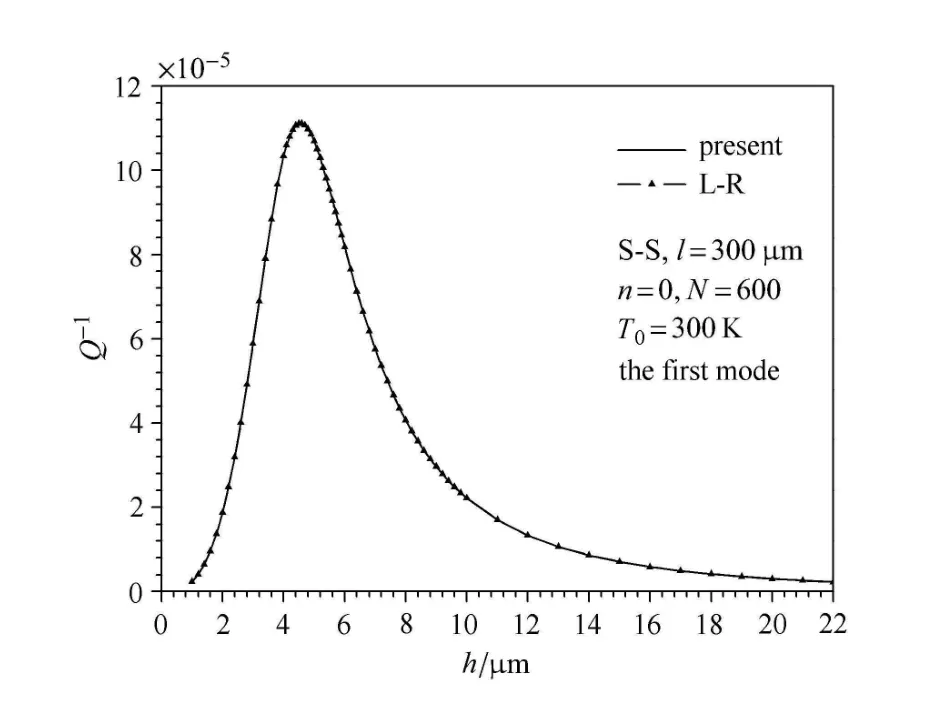
图2 本文所得纯陶瓷微梁的热弹性阻尼解答与文献中的解析解的比较Fig.2 A comparison of the present solution of TED for a pure ceramic micro beam with the analytical solution in the literature

图3 前三阶模态下FGM微梁的热弹性阻尼随厚度的变化曲线Fig.3 Curves of the thermoelastic damping of the FGM micro-beam versus the thickness in the firs three vibrating modes

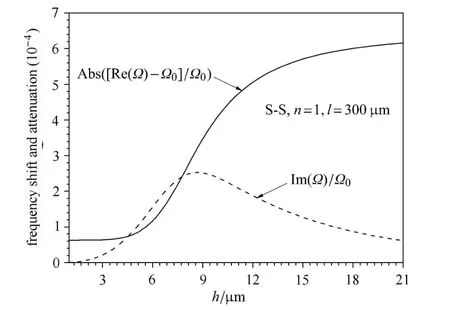
图4 FGM简支微梁自由振动时的频移和衰减随厚度的变化的关系曲线(一阶模态)Fig.4 The frequency shift and the attenuation change with the thickness of an S-S FGM micro-beam(in the firs mode)

对于FGM微梁，材料梯度变化指数n影响着材料的性质，从而会影响热弹性阻尼Q-1.在图5中，给出了两端简支FGM微梁在不同n值时对应的Q-1与h之间的关系.n=0代表纯陶瓷梁，n=105近似看作纯金属梁.从图中可以看出，整体上，随着n的不断增大,热弹性阻尼的最大值不断增大，且梁的临界厚度也不断增大.说明随着金属含量的增大，热弹性阻尼的最大值和临界厚度随之增大.图6给出了两端简支微梁在一阶模态下，不同厚度h对应的Q-1～n关系曲线.图6(a)～图6(c)的变化规律大致相同，在h=1,2,3µm时，Q-1都存在一个最小值点，此时谐振器的品质因子最高，即存在比单一组分材料梁更低的热弹性阻尼值.但从图6(d)中可见,在h=5,6,8,10µm时不存在热弹性阻尼的极小值.只有在材料性质趋近于陶瓷时热弹性阻尼才取得最小值.

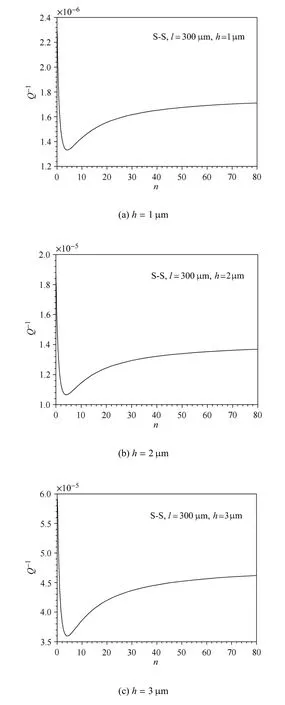
图6 给定不同厚度时FGM微梁的热弹性阻尼Q-1与材料梯度指数n之间的关系曲线(一阶模态)Fig.6 Thermoelastic dampingQ-1versus the material gradientnfor some specifie values of the thickness(in the firs mode)

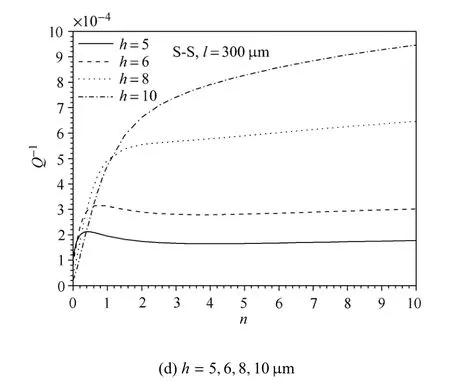
图6 给定不同厚度时FGM微梁的热弹性阻尼Q-1与材料梯度指数n之间的关系曲线(一阶模态)(续)Fig.6 Thermoelastic dampingQ-1versus the material gradientnfor some specifie values of the thickness(in the firs mode)(continued)

最后讨论边界条件对FGM微梁热弹性阻尼的影响.考虑两端夹紧(C-C)、一端夹紧一端简支(CS)、两端简支(S-S)、一端夹紧一端自由(C-F)四种边界条件.表3分别给出了以一阶模态振动时四种边界条件下的最大热弹性阻尼值及其所对应的梁厚hcr随材料梯度变化指数n的变化规律.从表中可以看出，在n值不变时，不同边界条件所对应的最大热弹性阻尼值相同，但是临界厚度却随着约束刚度的增大而减小.这说明，在几何尺寸和材料成分确定后边界条件不影响热弹性阻尼的最大值，只影响最大热弹性阻尼值对应的临界厚度.图7给出了一阶模态下，具有不同端部约束的FGM微梁对应的热弹性阻尼随厚度h连续变化的关系，从图中也可以证明表3中的结论.

表3 热弹性阻尼最大值和相应的临界厚度hcr(µm)值随材料梯度指数和边界条件的变化(一阶模态，l=300µm)Table 3 Values of the maximum TED,and the related critical thicknesshcr(µm)varying with the boundary conditions and for material gradient indexn(in the firs mode,l=300µm)

表3 热弹性阻尼最大值和相应的临界厚度hcr(µm)值随材料梯度指数和边界条件的变化(一阶模态，l=300µm)Table 3 Values of the maximum TED,and the related critical thicknesshcr(µm)varying with the boundary conditions and for material gradient indexn(in the firs mode,l=300µm)

BCsn0 0.1 0.2 0.5 1 4 10 100 100000 C-C Q-1max 1.1118 1.7682 2.3143 3.6068 5.0599 8.0746 10.0138 12.9454 13.4729hcr 3.47 4.13 4.60 5.60 6.60 8.16 8.53 8.72 8.75 C-S Q-1max 1.1118 1.7682 2.3143 3.6068 5.0599 8.0746 10.0138 12.9454 13.4729hcr 3.92 4.67 5.21 6.35 7.47 9.24 9.66 9.87 9.90 S-S Q-1max 1.1118 1.7682 2.3143 3.6068 5.0599 8.0746 10.0138 12.9454 13.4729hcr 4.55 5.42 6.05 7.36 8.67 10.73 11.20 11.45 11.49 C-F Q-1max 1.1118 1.7682 2.3143 3.6068 5.0599 8.0746 10.0138 12.9454 13.4729hcr 6.42 7.65 8.53 10.39 12.23 15.13 15.80 16.16 16.20

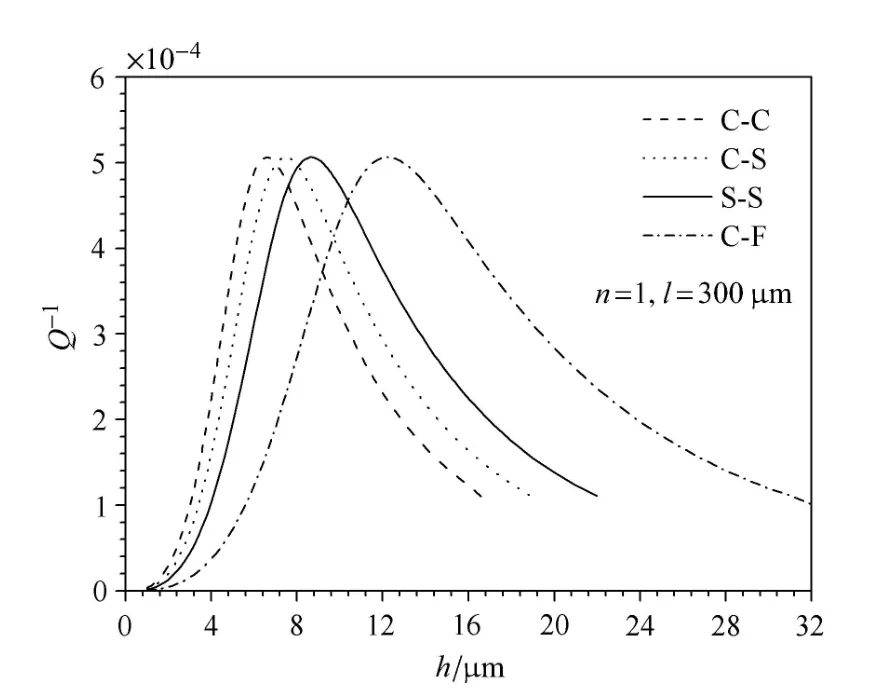
图7 不同边界条件下热弹性阻尼与厚度的关系曲线(一阶模态)Fig.7 Relationship curves between TED and the thickness under dif f erent boundary conditions(in the firs mode)

4 结论

基于 Euler-Bernoulli梁理论和各向同性非均匀介质热力耦合的热传导理论，研究了材料性质沿厚度方向连续变化的功能梯度材料微梁的热弹性阻尼.采用分层均匀化方法将变系数的热传导方程离散为定义在有限分层上的常系数热传导方程.从而在给定边界条件和界面处的连续性条件下求得温度场的分段连续解析解.将与振幅相关的温度场代入振动微分方程，采用复频率方法获得了热弹性阻尼的解析解.在纯陶瓷均匀梁的情况下，本文所得热弹性阻尼解答与相同条件下文献中的解答完全吻合.通过大量的数值结果，研究了几何尺寸、材料梯度指数、振动模态阶数以及边界条件等对FGM微梁的热弹性阻尼的影响，得到了以下结论：(1)若梁长固定不变，梁厚度小于某个数值时，改变陶瓷材料体积分数可以使得TED取得最小值；(2)固有频率阶数对TED的最大值没有影响，但是频率阶数越高对应的临界厚度越小；(3)不同的边界条件对应的TED的最大值相同，但是随着支座约束刚度增大对应的临界厚度减小；(4)TED的最大值和对应的临界厚度随着金属组分的增加而增加；(5)在理论上可以通过材料性质梯度变化优化设计减小微梁的热弹性阻尼.

1 Prabhakar S,Vengallatore S.Thermoelastic damping in bilayered micromechanical beam resonators.Journal of Micromechanics and Microengineering,2007,17:532-538

2 Tai YP,Li P,Zuo WL.An entropy based analytical model for thermoelastic damping in micromechanical resonators.Applied Mechanics and Materials,2012,159:46-50

3 Hendou RH,Mohammadi AK.Transient analysis of nonlinear Euler-Bernoulli micro-beam with thermoelastic damping,via nonlinear normal modes.Journal of Sound and Vibration,2014,333: 6224-6236

4 Lin SM.Analytical solutions for thermoelastic vibrations of beam resonators with viscous damping in non-Fourier model.International Journal of Mechanical Sciences,2014,87:26-35

5 Lifshitz R,Roukes ML.Thermoelastic damping in micro-and nanomechanical systems.Physical Review B,2000,61(8):5600-5609

6 Sun YX,Fang DN,Soh AK.Thermoelastic damping in micro-beam resonators.International Journal of Solids and Structures,2006,43: 3213-3229

7 Moosapour M,Hajabasi MA,Ehteshami H.Thermoelastic damping e ff ect analysis in micro fl xural resonator of atomic force microscopy.Applied Mathematical Modelling,2014,38:2716-2733

8 Guo X,Yi YB.Suppression of thermoelastic damping in MEMS beam resonators by piezoresistivity.Journal of Sound and Vibration,2014,333:1079-1095

9 Vengallatore S.Analysis of thermoelastic damping in laminated composite micromechanical beam resonators.Journal of Micromechanics and Microengineering,2005,15:2398-2404

10 Khisaeva ZF,Ostoja-Starzewski M.Theroelastic damping in nanomechanical resonators with finitwave speeds.Journal of Thermal Stresses,2006,29:201-216

11 Prabhakar S,Vengallatore S.Theory of thermoelastic damping in micromechanical resonators with two-dimensional heat conduction.Journal of Microelectro Mechanical Systems,2008,17(2):495-502

12 Parayil DV,Kulkarni SS,Pawaskar DN.Analytical and numerical solutions for thick beams with thermoelastic damping.International Journal of Mechanical Sciences,2015,94-95:10-19

13 Karami Mohammadi A,Ale Ali N.Vibrational behavior of an electrically actuated micro-beam with thermoelastic damping.Journal of Mechanics,2014,30(3):219-227

14 Kakhki EK,Hosseini SM,Tahani M.An analytical solution for thermoelastic damping in a micro-beam based on generalized theory of thermoelasticity and modifie couple stress theory.Applied Mathematical Modelling,2016,40:3164-3174

15 Zener C.Internal friction in solids I:theory of internal friction in reeds.Physical Review,1937,52:230-235

16 Zener C.Internal friction in solids II:general theory of thermoelastic internal friction.Physical Review,1938,53:90-99

17 Abbasnejad B,Rezazadeh G,Shabani R.Stability analysis of a capacitive FGM micro-beam using modifie couple stress theory.Acta Mechanica Solida Sinica,2013,26(4):427-440

18 Abbasnejad B,Rezazadeh G.Mechanical behavior of a FGM microbeam subjected to a nonlinear electrostatic pressure.International Journal of Mechanics and Materials in Design,2012,8:381-392

19 Rezaee M,Sharafkhani N,Chitsaz A.Electrostatically actuated FGM micro-tweezer under the thermal moment.Microsystem Technologies,2013,19:1829-1837

20 Zamanzadeh M,Rezazadeh G,Jafarsadeghi-poornaki I,et al.Static and dynamic stability modeling of a capacitive FGM micro-beam in presence of temperature changes.Applied Mathematical Modelling, 2013,37:6964-6978

21 Akgoz B,Civalek O.Free vibration analysis of axially functionally graded tapered Bernoulli-Euler microbeams based on the modifie couple stress theory.Composite Structures,2013,98:314-322

22 Li YL,Meguid SA,Fu YM,et al.Nonlinear analysis of thermally and electrically actuated functionally graded material microbeam.Proceedings of the Royal Society A,2013,470:0473

23 Jia XL,Zhang SM,Ke LL,et al.Thermal e ff ect on the pull-in instability of functionally graded micro-beams subjected to electrical actuation.Composite Structures,2014,116:136-146

24 AkgozB,CivalekO.Thermo-mechanicalbucklingbehavioroffunctionally graded microbeams embedded in elastic medium.International Journal of Engineering Science,2014,85:90-104

25 Akgoz B,Civalek O.Shear deformation beam models for functionally graded microbeams with new shear correction factors.Composite Structures,2014,112:214-225

26 李世荣，刘平.功能梯度梁与均匀梁静动态解间的相似转换.力学与实践，2010,32(5):45-49(Li Shirong,Liu Ping.Analogous transformation of static and dynamic solutions between functionally graded material beams and uniform beams.Mechanics in Engineering,2010,32(5):45-49(in Chinese))

ANALYSIS OF THERMOELASTIC DAMPING FOR FUNCTIONALLY GRADED MATERIAL MICRO-BEAM1)

Xu Xin Li Shirong2)
(School of Civil Science and Engineering，Yangzhou University，Yangzhou225127，Jiangsu，China)

Based on Euler-Bernoulli beam theory and the one-waycoupled heat conduction theory,thermoelastic damping (TED)of functionally graded material(FGM)micro-beams was studied.By assuming the material properties of the rectangular cross-section micro-beams to be varied continuously along the thickness direction as power law functions and ignoring the variation of the temperature gradient in the axial direction,one dimensional and one-way coupled heat conduction equation with variable coefficients was established.By using the layer wise homogenization approach,the heat conduction with variable coefficients was simplifie as a series of di ff erential equations define in each layer.The equation governing fl xural free vibration of the FGM micro beams subjected to time dependent non-uniform heating was developed on the basis of classical beam theory.By using the boundary conditions at the top and the bottom surfaces and the continuity conditions at the interfaces,analytical solution of the temperature fiel in the FGM micro-beams given layer wisely was obtained.Substituting the temperature fiel into equation of motion of the micro-beams,the complexfrequency including TED was achieved,and finall,values of the TED was extracted.Numerical results of the TED were calculated for the given values of physical and geometrical parameters of a metal-ceramic FGM beam.E ff ects of the material gradient,the geometry,frequency orders and the boundary conditions on TED were analyzed in detail.The results showed that:(1)if the beam length is fi ed,one can arrive at the minimum of the TED by changing the volume fraction of the ceramic when the beam thickness is less than a certain value;(2)the orders of the frequency have no influenc on the maximum of TED,however,the larger frequency corresponds to the smaller critical thickness(at which the TED reaches the maximum);(3)for di ff erent boundary conditions the maximums of TED are same,but the critical thickness is smaller for the stronger end constraints;(4)both the maximum of TED and the critical increase of the FGM micro beams increase along with the increment in the values of the volume fraction of the metal.

functionally graded material,micro-beams,thermoelastic damping,energy dissipation,free vibration

O343

A

10.6052/0459-1879-16-369

2016–12–08收稿，2017–01–10录用,2017–01–11网络版发表.

1)国家自然科学基金资助项目(11272278,11672260).

2)李世荣，教授，主要研究方向：结构非线性分析及新型材料结构力学行为.E-mail:srli@yzu.edu.cn

许新，李世荣.功能梯度材料微梁的热弹性阻尼研究.力学学报，2017,49(2):308-316

Xu Xin,Li Shirong.Analysis of thermoelastic damping for functionally graded material micro-beam.Chinese Journal of Theoretical and Applied Mechanics,2017,49(2):308-316