有“理”才能寓“意”，入“法”方能深刻

浙江省义乌市香山小学教育集团 朱天见

有“理”才能寓“意”，入“法”方能深刻

浙江省义乌市香山小学教育集团 朱天见

小学数学教师要通过开展数学活动，引导学生发掘一个数学问题；引导学生用数学思想来看待数学问题，了解数学问题中的规律；引导学生用抽象的数学公式来描述数学问题，这一数学公式就是数学问题的计算模式。

小学数学；数学模型；数学思想

小学数学教师在引导学生学习数学知识时，不仅要引导学生学会应用数学计算公式，还要引导学生理解数学公式应用的原因及这套数学思维形成的方法。数学教师只有应用这样的教学方法，才能让学生理解数学知识的本质。

一、通过丰富的教学活动来熟“法”悟“理”

数学教师在开展数学教学时，要应用开展数学活动的方法来开展数学教学。可以通过引导学生看到一个典型的数学案例，并在解决的过程中发现数学问题，并由此开始寻找解决数学问题的规律，继而理解数学规律背后的数学思想。

例如在教学《数学好玩》这节课时，我先让学生思考一个数学问题：现在给抽屉中放书。如果现在有3本书，放到两个抽屉中，那么必然有一个抽屉内有2本书；如果现有5本书，只有两个抽屉，那么至少有一个抽屉放三本书；如果现有7本书，有5个抽屉，那么依此规律每个抽屉至少要放几本书？很多学生刚开始的时候想当然地回答：“每个抽屉大概放3本书吧！因为3÷2的商是1，余数是1，于是1+2=3，5÷2的商是2，余数是1，于是2+1=3。那么可知7÷5的商是1，余数是2，于是1+2=3。”这时，我并没有直接点破学生的解题错误，只是引导学生动手去做一个简易抽屉，亲自动手实践。学生实践之后，发现自己的计算答案不对，如果现有7本书，有5个抽屉，那么每个抽屉至少要放2本书。为什么会得到这样的答案呢？之前的计算出现了什么错误呢？学生由此开始了探索和解决数学问题。

因此，在引导学生学习计算知识的时候，不能仅仅只引导学生学会应用计算公式。教师要应用丰富的教学活动开展数学教学，比如可以应用学生的认识冲突为学生提出一个数学问题，使学生开始思考数学认知的不足，只有这样，才能激发出学生的探索欲望，才能令学生愿意尝试去了解数学规律及数学本质。

二、通过新旧知识的迁移来“生成”算法

当学生在数学活动中发现了一个数学问题以后，教师不能直接告诉学生一个数学公式，让学生套用数学公式计算，而要结合学生学过的旧知识与生活实践，引导学生深入思考数学问题，使学生体验解决数学问题的整个过程。

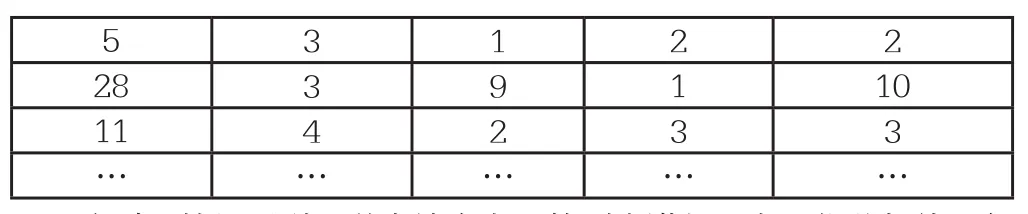
如引导学生学习《数学好玩》这节课时，当学生发现自己思考得出的数学答案不正确以后，陷入了迷惑中，很多学生不明白自己的答案为什么错了。这时，可以引导学生自己设计一个书本总数、抽屉数、每格至少放的书本数的表格，让学生尽可能列出各种放书的方案，再用刚才的计算方法来计算，并要求学生把计算的公式列出来。学生们列出的公式为表1：

表1 抽屉问题的数据统计

?

这时，教师再引导学生结合上面的列表进行思考：依此规律，每个抽屉里至少放的书本数与什么有关呢？学生经过思考，发现抽屉里至少放的书本数与商有关，而与余数无关。抽屉里至少放的书本数= 商+1，而不是商+余数。教师引导学生思考为什么抽屉里至少放的书本数不是商+余数，而是商+1呢？学生表示依此规律无论余数有多少，都要平均分配书本，于是这种分配方法不是抽屉里至少放的书本数为商+余数的关系，而是商+1的关系。当学生们完成了这一阶段的学习以后，了解到了当遇到复杂的问题时，可以用实践、绘表格、枚举的方法观察数学问题的规律。

因此，数学教师引导学生学习数学知识时，不能只是引导学生学会应用数学公式，而是要引导学生学会找到解决数学问题的方法，让学生从解决数学问题的方法入手，观察数学问题发生的规律，结合这一规律，学生便能找到解决数学问题的算式。

三、通过自主探究的过程来懂“理”归“法”

当学生理解了数学问题的规律以后，教师不能让学生把数学问题仅限于解决这一数学问题的层面，而要引导学生学习用抽象的思路看待数学问题。当学生学会用抽象的思路看到数学问题以后，就能把算式变成公式，这一公式将是解决数学问题的模型，这也是解决这类数学问题的核心思路。

如在引导学生学习《数学好玩》这节课时，引导学生思考：现在如果用字母的方式来表达刚才数学问题的计算方法，可以如何进行归纳呢？

学生经过思考，尝试着把字母代入到以上的数学计算公式中，并列出了数学计算公式为S=m÷n=a……b。其中S为书本总数，a为总书本数÷抽屉数的商，b为总书本数÷抽屉数的余数，这一规则中抽屉里每格放书本数的计算方法为a+1。学生觉得这就完成数学问题的描述了，但我仍旧继续引导学生思考：以上的数学公式中，字母表示的范围有没有限制呢？学生经过教师的引导，继续整理公式，添加了“其中0＜b＞n”的限制。这时，我又引导学生继续思考：以上的数学描述简练不简练？准确不准确？于是学生尝试用更抽象的角度来思考以上的算式。学生在完成了这一阶段的学习后，发现列出这一数学计算公式以后，只要遇到同一问题，可以直接套用数学公式计算。因此，数学教师在开展数学教学活动的时候，不仅要引导学生找到数学问题的规律，还要引导学生学会建立简单的数学模型，当学生能应用抽象的语言描述出数学问题的计算规律，建立一个抽象的数学模型以后，就能应用抽象的数学模型解决这一类的数学问题，这个数学模型就是数学问题提出及解决方案的核心本质。

总之，数学教师在开展数学教学时，要通过开展数学活动来了解一个数学问题，引导学生学会应用数学思想来分析数学问题中的规律，能从抽象的角度把数学规律整合成一个数学模式。只要学生长期受到这样的训练，思维水平就能提高，数学学习水平也就能提高。