基于流溪河模型的梅江流域洪水预报研究

王幻宇，陈洋波，覃建明，李明亮，董礼明

(1.中山大学地理科学与规划学院，广州，510275; 2.江西省赣州市水文局，江西 赣州 341000)

0 引 言

梅江亦称梅川，古称汉水，又称宁都江，系赣江一级支流，流域内呈北高南低的不规则扇形。发源于宁都、宜黄两县交界的王陂嶂南麓，自北向南贯穿宁都县腹地，经瑞金市瑞林乡，过于都县曲阳等七个乡镇，至于都县贡江镇龙舌咀注入贡水。宁都水文站断面以上集水面积2 372 km2，流域形似竹叶，主河长79 km。流域属亚热带季风区，多年平均降雨量1 640 mm，降雨主要集中在3-9月，暴雨类型主要有锋面雨、地形雨、台风雨，汛期洪水陡涨陡落，是江西省典型的中小流域。宁都水文站设立于1958年11月，站址在宁都县梅江镇东门外。河段较顺直，河床细沙组成，上游约300 m处有竹坑河汇入，上游约700 m处有会同河汇入，上游团结水库坝址距水文站站49 km。本文以宁都水文站以上流域开展研究，以下简称梅江流域。

流溪河模型[1-3]是一个主要应用于流域洪水预报的分布式物理水文模型，模型将流域划分为若干单元流域，各单元流域上产生的径流量通过汇流网络进行逐单元汇流至流域出口，汇流分成边坡汇流和河道汇流，分别采用运动波法和扩散波法进行计算。流溪河模型提出了基于PSO法的模型参数自动优选方法[3,4]，实际应用中只要有一场具有代表性的实测洪水就可以优选模型参数。采用精细化的汇流计算方法和高效率的参数优选技术，使得流溪河模型在我国中小河流洪水预报中应用具有很好的应用潜力。流溪河模型已成功应用于水库洪水预报[5]、中小河流洪水预报[6]、大流域水文气象耦合洪水预报[7]。

为了探讨流溪河模型在梅江流域洪水预报中的适用性，提高模型在中小河流洪水模拟的效果。本文基于90 m×90 m的DEM数据，分别构建了1级、2级、3级河道的梅江流域洪水预报模型，采用PSO算法进行模型参数优选，对不同河道分级建立的流溪河模型进行了验证。结果表明，河道分级对中小河流洪水过程的影响较大，1级河道的模型不能充分表达流域洪水演进过程，3级河道可以满足模型计算精度要求。采用3级河道构建的梅江流域洪水预报流溪河模型对50场洪水进行模拟验证，模拟效果优良，该方案可用于梅江流域实时洪水预报。

1 梅江流域洪水预报流溪河模型构建

1.1 梅江流域洪水资料

梅江流域内有22个雨量站，流域出口处的宁都水文站有较长期的水文观测资料，站点分布见图1。本文收集了梅江流域内1971年以来的51场实测洪水过程的资料，包括雨量站降雨及水文站流量，均以小时为时段。将洪峰流量小于700 m3/s的洪水定义为小洪水，洪峰流量大于1 500 m3/s的洪水定义为大洪水，其他洪水定义为中洪水。则共有小洪水10场，中洪水21场，大洪水20场，都具有较好的代表性。

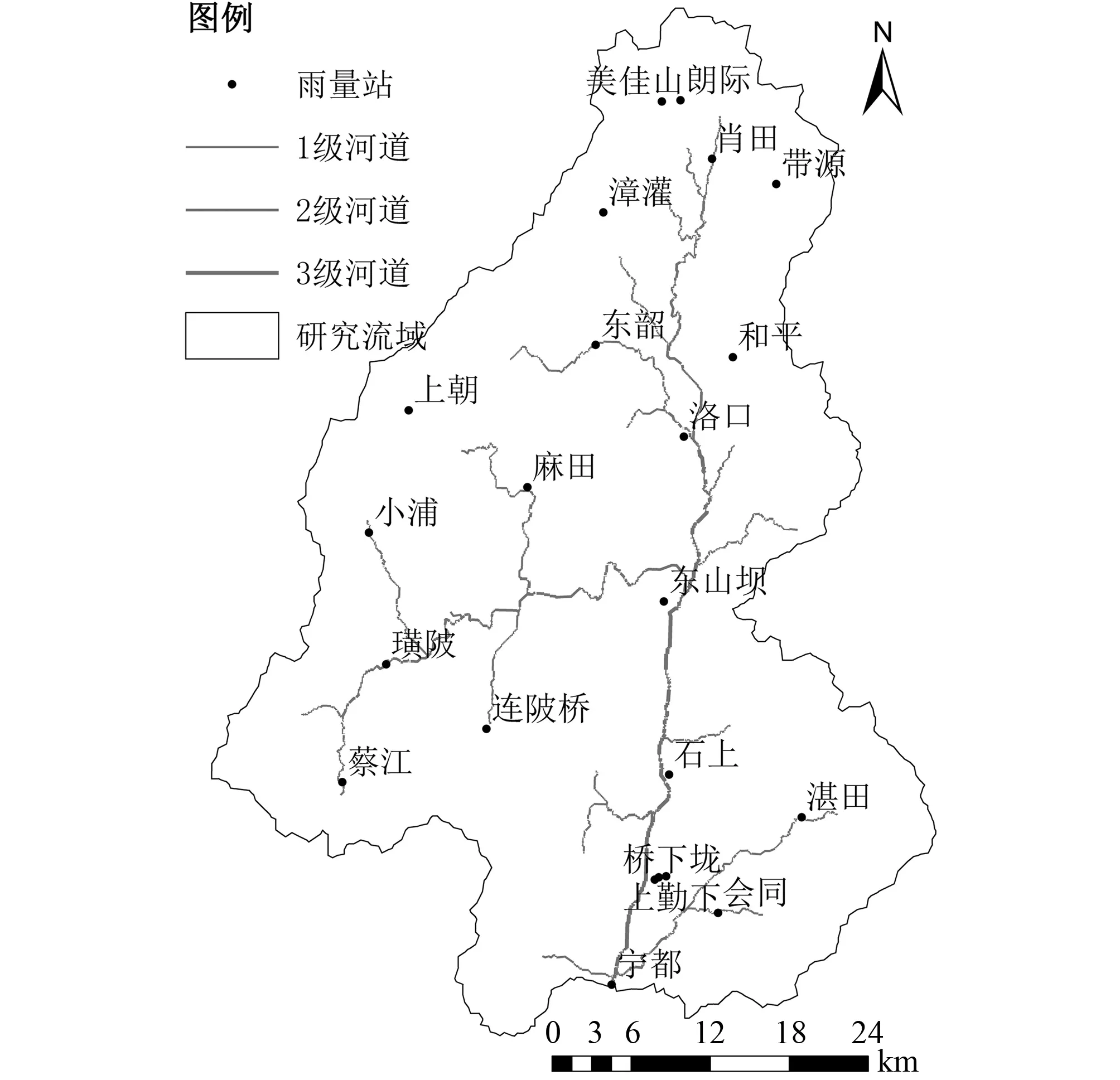
图1 梅江流域水情遥测站网分布图

1.2 流溪河模型构建

流溪河模型建模所需的DEM数据采用SRTM(http:∥srtm.csi.cgiar.org/)公共数据库中的数据。土地利用类型为美国地质调查局全球土地覆盖数据库中的数据 (http:∥landcover.usgs.gov/)，包括常绿针叶林、常绿阔叶林、灌丛、高山和亚高山草甸、湖泊和耕地，土壤类型采用国际粮农组织的土壤数据(http:∥www.isric.org/)，主要土壤类型有CN10033、CN10097和CN10647等。空间分辨率都采用90 m×90 m，见图2。

流溪河模型基于D8流向法[8,9]划分边坡单元和河道单元，根据DEM计算确定各个单元的累积流值，并设定一系列的累积流的阀值，对于累积流大于阀值的单元，被划分成河道单元，对于累积流值小于阀值的单元，被划分成边坡单元。由于在划分河道单元时，累积流阀值的选用对计算结果的影响较大，为了避免累积流阀值选用时的不确定性，在对河道单元进行划分时，流溪河模型根据strahler[10]方法将河道分级，根据河道分级的情况确定相应的河道单元划分结果。

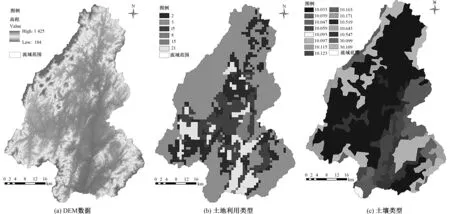
图2 梅江流域特性数据

针对梅江流域，对累积流阀值FA0取了不同的值将河道分为1、2、3级。采用分段点将河道划分为若干虚拟河段，并假定同一虚拟河段的河道属性一致。不同河道分级的分段点数量不同，随着河道分级的增加，河道的分段点就会增多，虚拟河段的段数也在增加，模型对流域河道的刻画就越清晰，见表1。但是当河道分级增加到4级时，利用卫星遥感影像对4级河道进行分析可以发现，水系末端的河道形态不明显，跟实际的流域水系分布不符，所以本文采用的最高级河道为3级。基于1、2、3级河道分别构建梅江流域洪水预报流溪河模型，见图3。

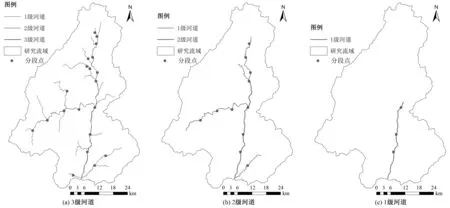
图3 流溪河模型结构示意图

河道分级河道单元数边坡单元数结点数虚拟河段数137230370034213833026891114329293011432045

1.3 流溪河模型初始参数推求

流溪河模型基于各单元上的流域物理特性确定模型初始参数，对不同河道分级建立的模型，据此确定的模型初始参数相同。参数分成4大类，包括地形类参数，气象类参数，土壤类参数和土地利用类参数。流向和坡度是流溪河模型的地形类参数，根据DEM直接计算确定，不再调整，是不可调参数。气象类参数主要是蒸发能力，根据经验，所有单元均取为5 mm/d。土地利用类型参数是边坡糙率和蒸发系数。蒸发系数是个非常不敏感的参数，根据流溪河模型参数化经验，统一取为0.7。边坡糙率根据文献[11]推荐值确定。

土壤类参数包括土壤厚度、饱和含水率、田间持水率、饱和水力传导率、凋萎含水率和土壤特性。饱和含水率、田间持水率、饱和水力传导率和凋萎含水率采用由Arya等人提出的土壤水力特性计算器[12]计算，结果如表2。土壤特性统一取为2.5。

2 模型参数优选

在流溪河模型中，根据DEM将流域划分成正方形的单元流域，本文将梅江流域按90 m分辨率的DEM分成了304 072个单元流域，每个单元上共有13个参数，导致模型进行参数优选时计算工作量非常大。每个单元流域参数都存在不确定性，当成千上万的单元流域不确定性累积叠加将会影响到分布式模型的模拟效果，而且洪水预报对模型模拟的精度要求较高，导致分布式模型在洪水预报中应用时受到限制。

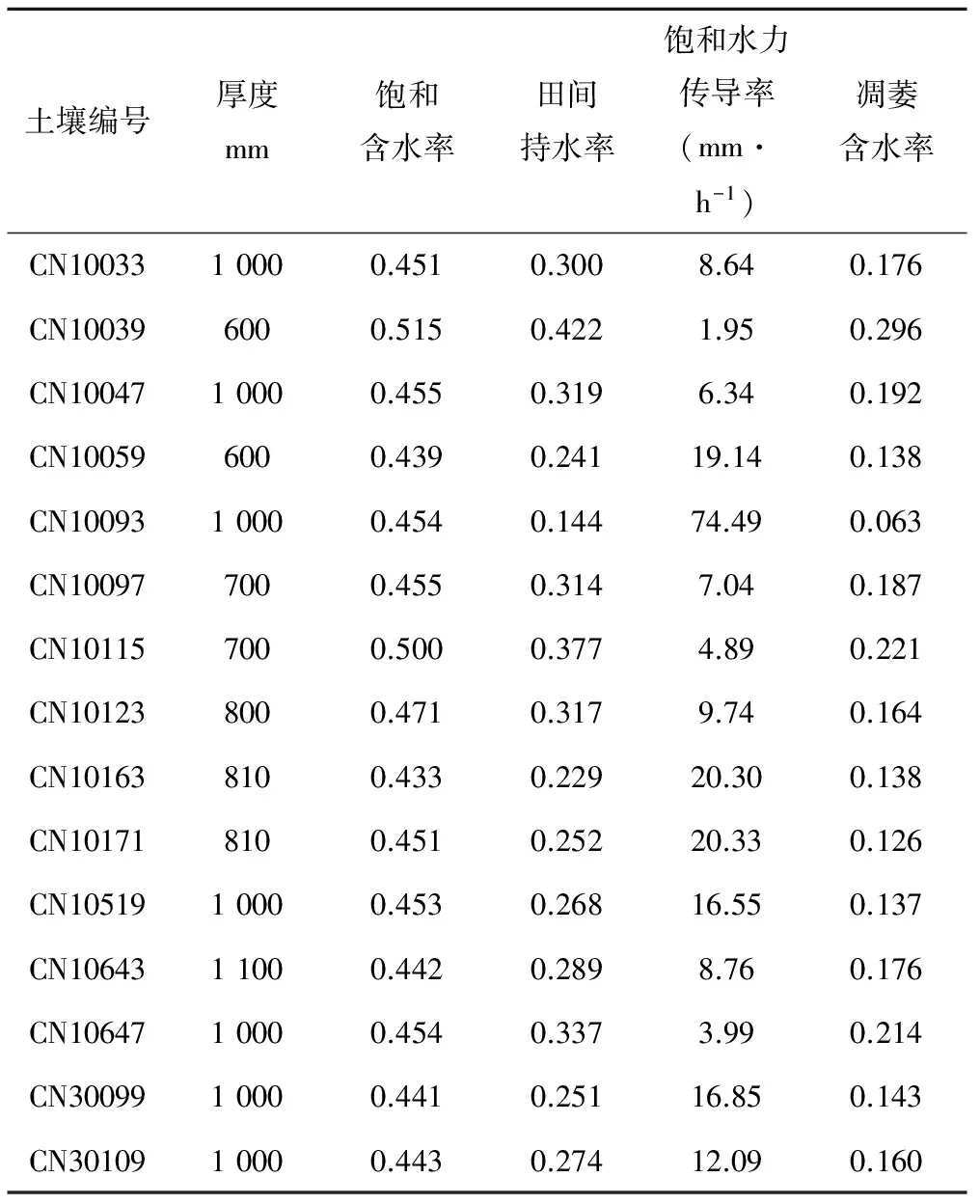
表2 土壤类参数初值

流溪河模型采用PSO法进行模型参数自动优选，采用一场实测洪水进行模型参数优选就可以获取较优的模型参数，有效提高了模型的性能。本文以2012062119场次洪水进行模型参数优选，其他50场次洪水进行模型验证。对不同的河道分级，本文均采用2012062119场次洪水进行参数优选，优选的模型参数各不相同。限于篇幅，图4仅列出了3级河道参数优选过程中适应值和参数值的进化结果。从图4中看出，经过20次的进化计算，模型参数收敛到最优值，说明流溪河模型参数优选具有较好的收敛速度。优选的洪水过程与实测洪水拟合程度非常高，确定性系数高达0.943，相关性系数为0.978，过程相对误差为0.18，峰值误差为0.042，水量平衡系数为0.935，峰现时间差为-5，模拟结果见图5。

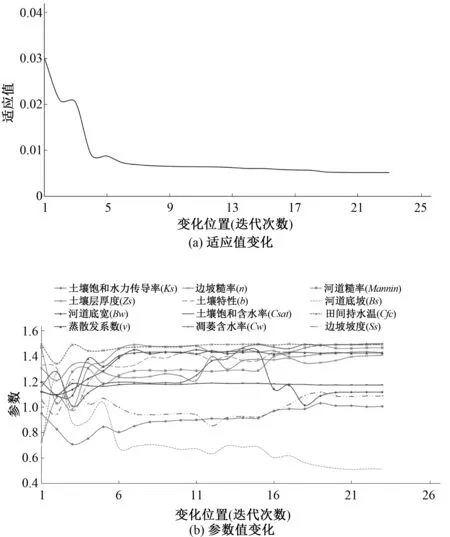
图4 参数优选过程中参数进化图(3级河道)

图5 优选的洪水过程线(3级河道)

3 模型验证

采用1、2、3级河道建立的流溪河模型及相应的优选参数，分别对50场洪水进行了模拟，统计了模拟的各场洪水的6个评价指标。由于数据较多，表3仅列出了各级模型的平均统计指标，图6仅绘出了其中6场洪水的模拟结果。

表3 不同河道分级的流溪河模型洪水模拟结果统计指标表

从统计指标和模拟过程可以看出，3级河道的模型模拟效果最好。说明3级河道充分刻画了洪水的河道汇流演进过程，可以满足中小河流洪水模拟的精度要求。2级河道的模型模拟效果也不错，比3级河道的模型效果稍差，而且2、3级河道的模型的总体性能都较好，同时也说明了参数优选能降低河道分级不确定性对模型洪水模拟的影响。1级河道的模型模拟效果较差，模拟洪水过程与实测值的拟合程度不高，模拟得到的洪水峰值低于实测值，峰值误差比2、3级河道的模型都高，不能很好地模拟实测洪水峰值。梅江流域的洪水主要由暴雨引起，洪水陡涨陡落，是典型的中小河流洪水。而中小河流洪水防治的重要指标是洪峰流量，是中小河流洪水预报的关键。因此可以认为，1级河道的模型不能充分刻画河道汇流过程，影响到模型模拟的精度，在进行中小河流洪水预报应用时不宜采用；3级河道的模型可比较理想的模拟实测洪水过程，说明3级河道划分已能充分刻画中小河流洪水过程中的河道汇流特征，模拟结果满足实际洪水预报的精度要求。

本文采用河道分级为3级，河道断面形状为矩形时的梅江流域洪水预报流溪河模型，参数采用优选的模型参数。该方案对50场洪水模拟的确定性系数均值为0.51，相关系数达0.87，洪峰误差均值为5.64%，最大的也没有超过20%，平均峰现时间为-3.2小时，洪水过程的模拟结果与实测值吻合很好。根据我国水文情报预报规范，该预报方案等级可评定为甲等，可用于梅江流域实时洪水预报。

4 结 语

为了探讨流溪河模型在中小河流实时洪水预报中的适用性，本文以江西省梅江流域为研究对象，基于90 m×90 m的DEM数据构建了1、2、3级河道的梅江流域洪水预报流溪河模型，采用PSO算法优选模型参数，并对不同河道分级的模型进行了验证。结果表明，河道分级对中小河流洪水过程的影响较大，1级河道建立的模型不能较好地模拟出实测洪水过程，尤其是洪水峰值流量的模拟，不能满足模型在中小河流洪水预报中的计算要求。3级河道构建的模型可以很好地模拟实测洪水过程，采用流溪河模型进行中小河流洪水预报时，可以以3级河道构建模型；流溪河模型采用1场洪水就可以对模型参数进行有效优选，在实测资料系列不长的我国中小河流洪水预报中应用具有明显优势；采用3级河道构建梅江流域洪水预报流溪河模型和优选的模型参数，模拟效果良好，可用于梅江流域实时洪水预报。

分布式水文模型由于模型结构复杂、参数难以率定、模型计算量大等原因，导致大部分的分布式模型不能应用到流域实时洪水预报中。本文构建不同河道分级的梅江流域洪水预报流溪河模型，采用PSO优选模型参数，并进行了模型验证。明确了采用流溪河模型进行中小河流实时洪水预报时，采用3级河道构建模型和采用PSO算法优选模型参数的方法是可行的。本文的研究可为分布式水文模型在中小河流洪水预报中的应用提供参考和借鉴。

□

[1] 陈洋波. 流溪河模型[M]. 北京：科学出版社,2009.

[1] 陈洋波,任启伟,徐会军,等.流溪河模型I:原理与方法[J].中山大学学报(自然科学版), 2010,49(1):105-112.

[2] 陈洋波,任启伟,徐会军,等.流溪河模型II:参数确定[J].中山大学学报(自然科学版), 2010,49(2):105-112.

[3] Yangbo Chen, Ji Li, Huijun Xu. Improving flood forecasting capability of physically based distributed hydrological model by parameter optimization [J]. Hydrology & Earth System Sciences, 2017,21:1 279-1 294.

[4] 陈洋波,徐会军,李 计.流域洪水预报分布式模型参数自动优选[J].中山大学学报(自然科学版),2017,56(3):15-23.

[5] 黄家宝,董礼明,陈洋波,等.基于流溪河模型的乐昌峡水库入库洪水预报模型研究[J].水利水电技术,2017,48(4):1-12.

[6] 陈洋波,覃建明,王幻宇,等.基于流溪河模型的中小河流洪水预报方法[J].水利水电技术,2017,48(7):12-27.

[7] Yangbo Chen, Ji Li, Huanyu Wang, et al. Large-watershed flood forecasting with high-resolution distributed hydrological model [J]. Hydrology & Earth System Sciences, 2017, 21:735-749.

[8] Ji Li, Yangbo Chen, Huanyu Wang, et al. Extending flood forecasting lead time in a large watershed by coupling WRF QPF with a distributed hydrological model [J]. Hydrology & Earth System Sciences, 2017, 21:735-749.

[9] O'Callaghan J, Mark D M. The extraction of drainage networks from digital elevation data [J]. Comput. Vis. Graph. Image Process, 1984,28(3):323-344.

[10] Strahler A N.Quantitative Analysis of watershed Geomorphology[J].Transactions of the American Geophysical Union, 1957,35(6):913-920.

[11] Wang Z, Batelaan O, De Smedt F. A distributed model for Water and Energy Transfer between Soil, Plants and Atmosphere (WetSpa) [J]. Phys. Chem. Earth,1996,21:189-193.

[12] Arya L M, J F Paris. A physioempirical model to predict the soil moisture characteristic from particle-size distribution and bulk density data[J].Soil Sci. Soc. Am. J,1981,45:1 023-1 030.