一种利用流量过程线估算新安江模型分水源参数的方法

童冰星，姚 成，黄小祥

(河海大学水文水资源学院，南京 210098)

1 研究背景与概述

在新安江模型[1-5]的应用中，自由水蓄水库的容量(SM)、壤中水径流出流系数(KI)与地下水径流出流系数(KG)这几个主要的分水源参数决定了径流成分比例[6,7]，它们的些微改变可能会引起流域出口的径流过程线形状的较大变化[8-10]。一般情况下需要通过实测资料率定分水源参数。然而，新安江模型参数多达17个。大量的待定参数往往会导致“异参同效”现象的发生[11-13]。这样不仅使得率定出的分水源参数可能不准确，而且，过多参数使得模型在应用时需要较为烦琐的调参工作，给模型的使用带来不便。如何用简便且具有一定物理基础的方法获得合理的新安江模型分水源参数的值，减少所需要率定的参数，在一定程度上降低“异参同效”对模型的影响，正是本文需要解决的问题。

流域出口的流量过程线实际上是降雨受流域下垫面调蓄作用后在流域出口一种具体表现。本文从实测流量过程出发，提出了一种利用流量过程线来直接估算分水源参数值的方法，并将该方法分析得到的SM、KI与KG的值用于新安江模型，通过模型在洪水模拟中的应用来验证这种方法。

2 通过实测流量过程估算分水源参数

基于山坡水文学中的产流与分水源理论可知，壤中水径流产生于土壤表层较为疏松的土层与深层较为密实的土层之间，该土层通常被称作腐殖质土层。且自由水蓄水容量(SM)的值与腐殖质土层厚度紧密相关。本文通过建立壤中水径流(RI)与自由水蓄水容量(SM)之间的函数关系来达到从实测流量过程出发直接估算分水源参数值的目的。

估算SM的值：首先在流域出口的流量过程线上依据退水段的斜率变化划分出地表水，壤中水和地下水径流(图1)，由此计算出壤中水径流深RI，在选择实测流量过程线时一般选取独立的单次洪峰，以方便径流的划分；其次借鉴产流过程中通常用径流深与降雨深的比值(R/PE)来表示流域产流面积比例的方法，本文采用地表径流深与降雨深的比值(RS/PE)作为流域上自由水蓄水库蓄满的面积比例，并用FRR来表示[式(1)]；同时由于在自由水蓄水库蓄满(R+S≥SM)时产生的壤中水的深度恰好等于自由水蓄水容量与壤中流出流系数的乘积[16]，而自由水蓄水库蓄满的标志为产生地表径流，即在流域上产生地表径流的区域上式(1)成立。

(1)

式中：FRR为全流域上自由水蓄水库蓄满的面积比例；RS为径流划分得到的地表径流深；PE为降雨减去蒸发之后的雨深。

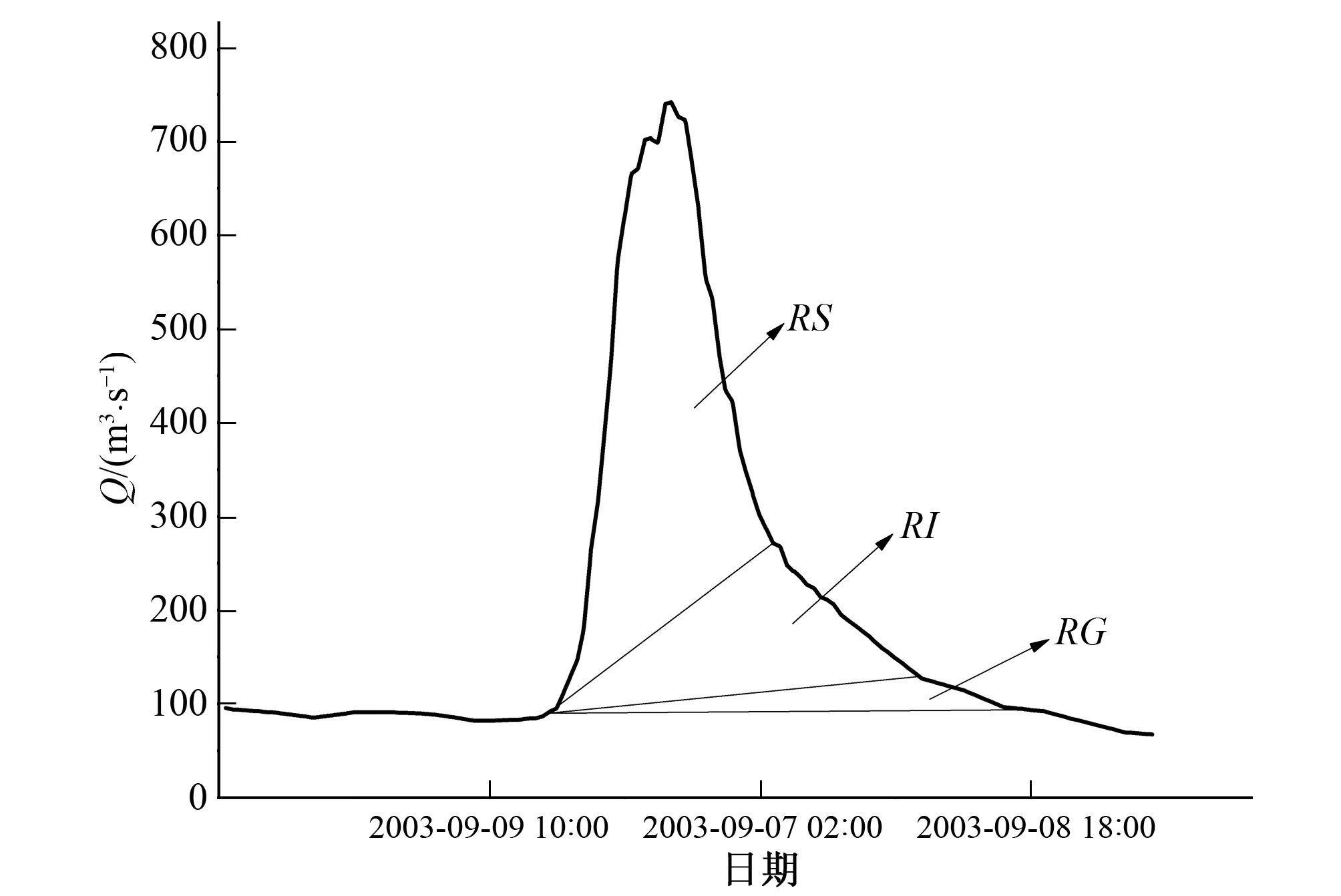
图1 径流成分划分Fig.1 Partition different runoff components

在流域上蓄满的区域上有：

RI=KISM

(2)

式中：SM为流域平均自由水蓄水容量，RI为壤中水径流，KI为壤中流出流系数。

最后结合式(1)和式(2)的基础上得到洪水过程中全流域上壤中水径流深(RI)与自由水蓄水容量(SM)之间的函数关系[式(3)]。

(3)

其中， 对于RI，本文在流域出口的流量过程线上依据退水段的斜率变化划分出地表水，壤中水和地下水径流(图1)，由此可以计算出壤中水径流深；

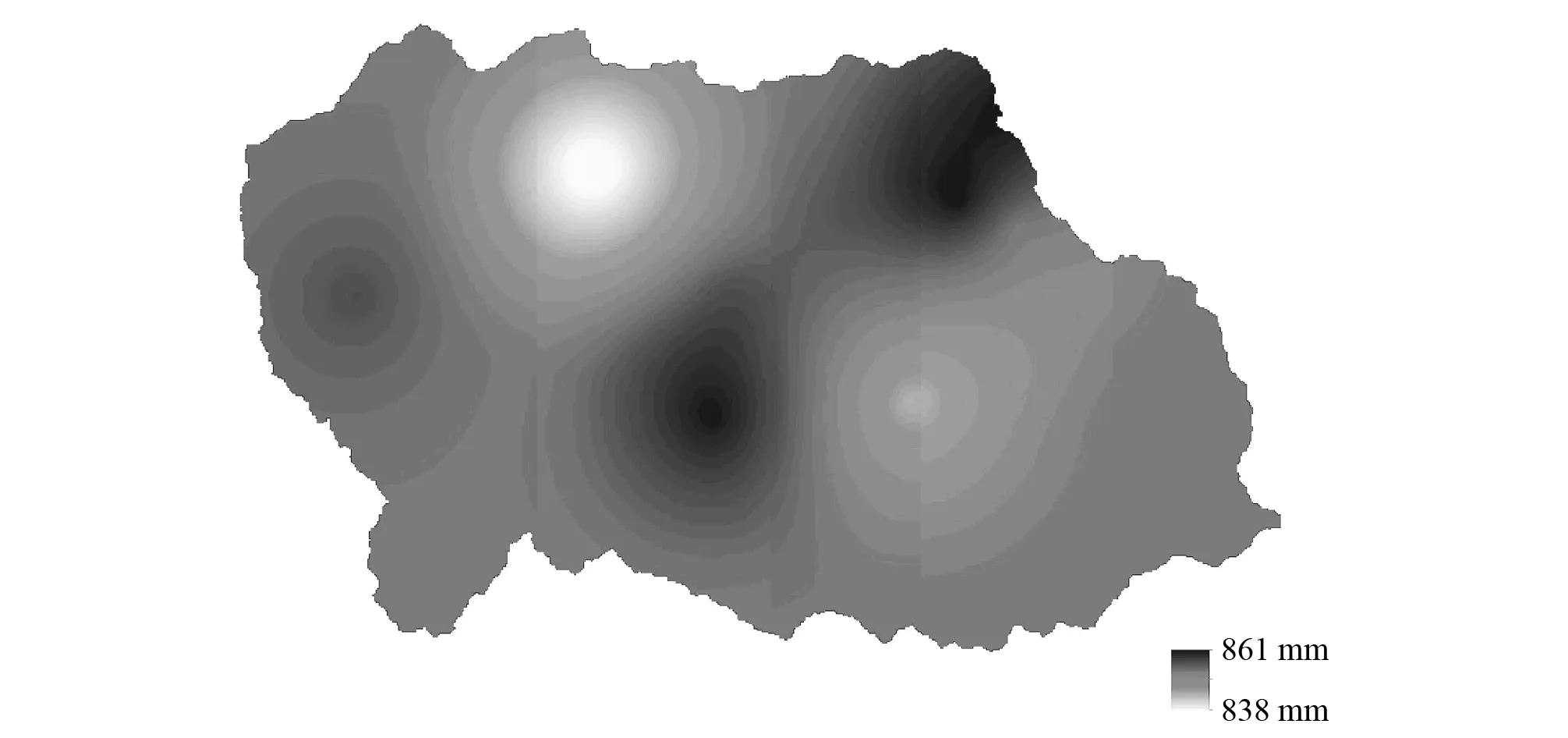
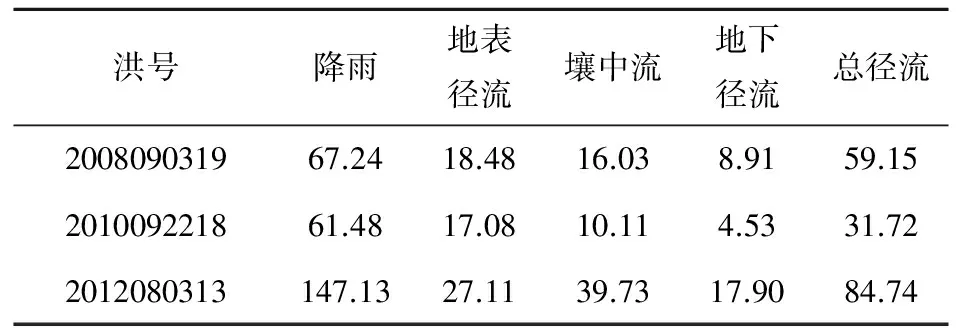
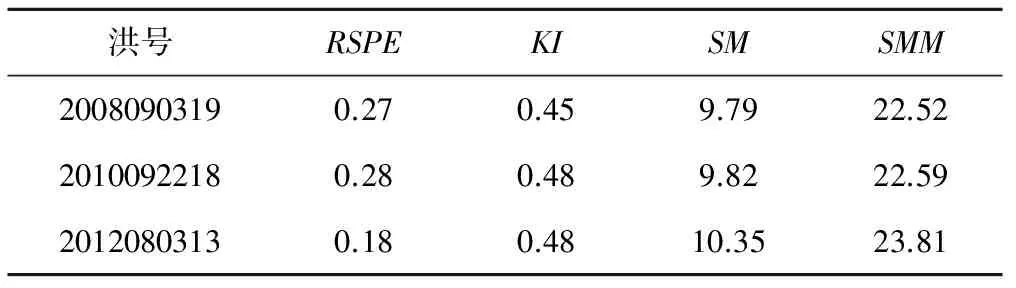
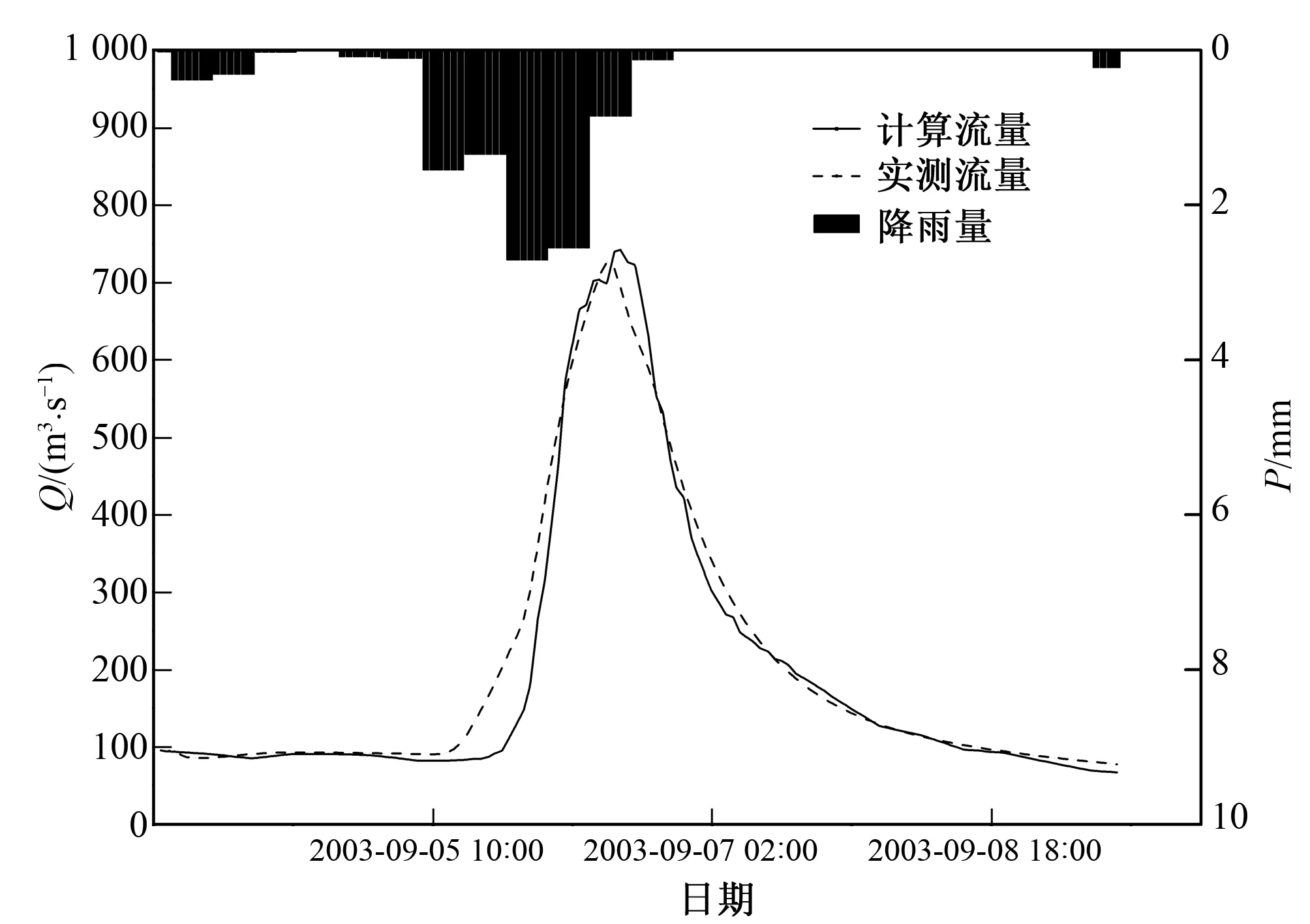
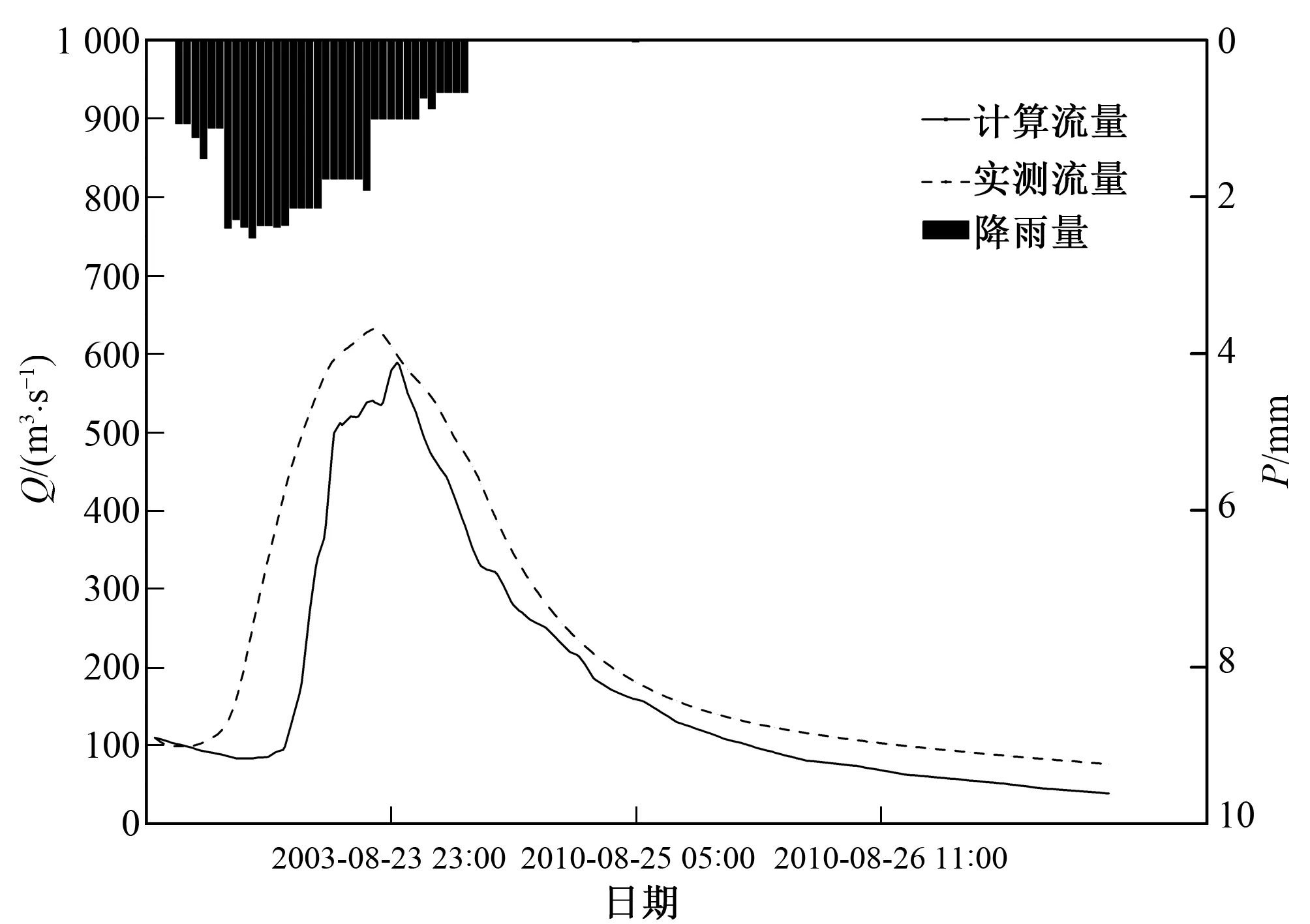
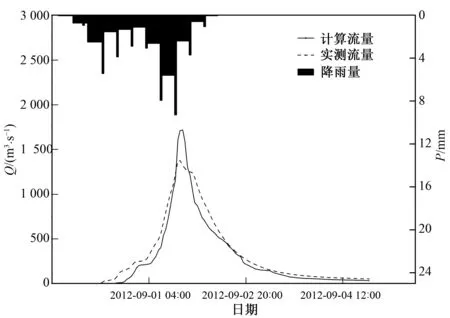
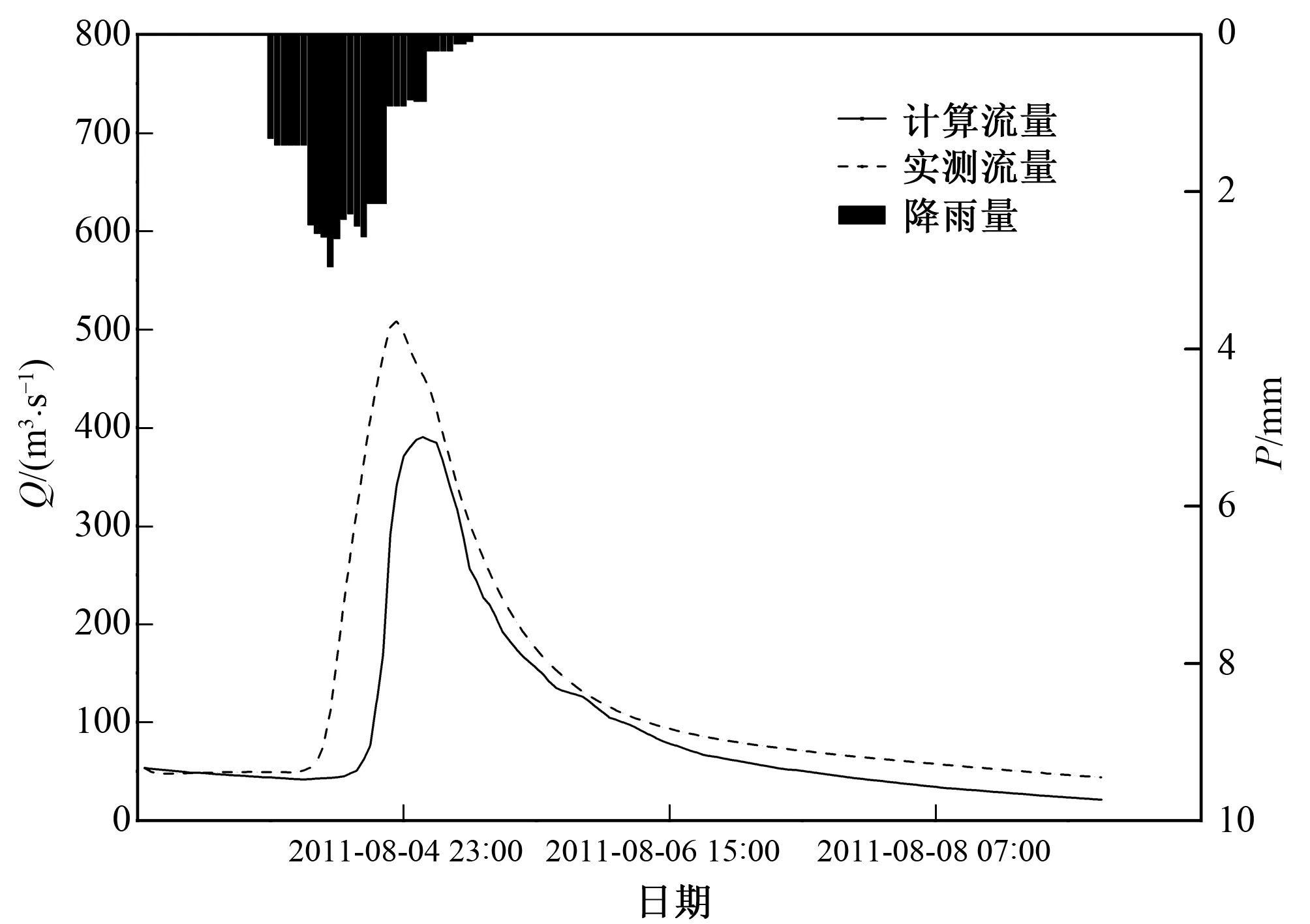
估算KI的值：对于KI，发现无论是在R+S≥SM时还是在R+S

(4)

在此需要说明的是本方法并不能适用于所有的流域，由于本文所提出的估算分水源参数地方法与新安江模型中的产流计算理论紧密相关，而新安江模型适用于湿润流域或半湿润流域，因此本方法在湿润流域或半湿润流域的应用效果较好。

3 研究区域概况

本文选择位于陕西省黑河流域的陈河流域作为研究流域(图2)。黑河发源于秦岭北麓，太白山主峰东侧，自西南向东北汇入渭河，是渭河水系的一级支流，流域面积2 249.7 km2，河长126 km。流域山高、坡陡、水流湍急。黑河为渭河南岸较大支流，沿途较大的支流有大莽河，板房子河，虎豹河，王家河，河系呈扇形排列，除大莽河外，其余支流均在右岸。

流域位于北温带，属大陆性季风气候，多年平均降水量700～900 mm，河流水量主要系雨水补给，局部暴雨是发生洪水的主要原因。且陈河流域地处秦岭北麓，为秦岭褶皱带，上游大部分为高中山区，海拔高程700～3 500 m，山势雄伟，重峦叠嶂，峰谷相间，平均坡度在40°～60°。流域内属暖温带落叶阔叶林及针阔混合林带，林相的垂直分布规律比较明显，流域森林覆盖率为82%。流域在地质耕造上属北秦岭褶皱带。主要建造岩为：变质混合岩类、花岗岩体也有零星分布。土壤分布由下到上有黄褐土、褐土、褐棕壤、高山草甸土。由于母岩的风化，流域表层有沙性土壤分布。

综上可知陈河流域降雨较为丰富(图3)，适用于本方法。且流域山高坡陡，植被丰富，这些因素使得流域具有较好的降雨产流条件，年平均径流深达100～500 mm，径流系数0.2～0.5，属于相对较高产流区。

图2 陈河流域DEMFig.2 DEM of Chenhe catchment

图3 流域多年平均降雨量分布Fig.3 The average rainfall for previous years in Chenhe catchment

4 方法验证

陈河流域2003-2012年这10 a间雨量站，水文站的站址均未发生较大的变动，且各雨量站降雨资料、流量资料齐全，其余年份缺少部分雨量站的雨量资料，故本文选取2003-2012年10年中共17场洪水进行模拟计算。在选择洪水时尽量保证大、中、小洪水全面选择，并且各种峰形及历时长短的洪水尽量覆盖，以保证本方法的普遍适用性。

本文将17场洪水按照洪峰由大到小的顺序进行排序，分别选取排序大致位于25%，50%以及75%的2012080313号，2008090319号和2010092218号洪水作为研究示例。在3场洪水产生的实测流量过程线上分别划分地表径流，壤中水径流和地下径流(表1)，用本文提出的方法来计算陈河流域的自由水蓄水容量(SM)、壤中水径流出流系数(KI)与地下水出流系数(KG)的值(表2)，将它们带入新安江模型中进行模拟演算。

表1 径流成分划分表 mm

表2 计算结果表Tab.2 The results of Calculations

由上面的三场洪水计算得到的SM取平均值，得到陈河流域的SM为9.99，SMM为22.97。

由上面的三场洪水计算得到的KI取平均值，得到陈河流域的KI为0.47。即依据KI与KG之间的线性约束关系可以得到KG的值是0.23。

将求得的SM、KI以及KG的值代入新安江模型中，同时率定其他敏感参数(表3)。

表3 新安江模型率定参数表Tab.3 Parameters of Xin'anjiang model

将率定出来的参数带入新安江模型中进行洪水模拟。并将模拟演算的结果与实测流量资料作比较(表4)。并根据《GB/T 22482-2008水文情报预报规范》，从径流深误差、洪峰误差、峰现时间误差以及确定性系数这几个方面来对于模型的模拟结果进行评价。

表4 洪水模拟结果表Tab.4 Results of flood simulation

如图4～图6依据《GB/T 22482-2008水文情报预报规范》的要求，在陈河流域中2003年到2012年间的17场洪水中：有15场洪水径流深相对误差小于20%，径流深合格率为88%，平均模拟径流深相对误差为15.23%。有16场洪水洪峰相对误差小于20%，模拟洪峰合格率为94%，平均模拟洪峰相对误差为10.7%。17场洪水的确定性系数均大于0.6，其中大于等于0.9的有5场；大于等于0.7小于0.9的有13场。

图4 2008090319号洪水过程Fig.4 Simulated result and measured result of flood in September 3-9(2008)

图5 2010092218号洪水过程Fig.5 Simulated result and measured result of flood in September 22-27(2010)

图6 2012083013号洪水过程Fig.6 Simulated result and measured result of flood in August 30-9(2012)

由以上结果统计可知模拟计算的总体效果良好，但是如图可见，2011080301号洪水计算的径流深和洪峰均明显偏大，在查阅这场洪水前后时间段的资料时发现：2011080301号洪水前长期无雨，土壤干燥，且8月正值夏季，流域内植被茂盛，同时生产生活需水量较大，这些因素综合导致该时间段内的降雨和径流大量被植被，土壤以及人为作用拦蓄，使得计算的径流深与洪峰明显偏小。

图7 2011080301号洪水过程Fig.7 Simulated result and measured result of flood in August 3-9(2011)

同时表4中2010072101号、2012083013号以及2006090308号洪水也有较大误差，进一步调查研究发现：2010072101号洪水由于人为作用的影响，使得大量径流被拦蓄，干扰了流域内的水文规律，导致计算的径流深偏大，误差高达26.5%。而对于2012083013号洪水和2006090308号洪水，虽然降雨量不大，但是由于降雨中心的位置在流域下游出口处附近，导致洪水迅速涨落，模型模拟效果并不是十分理想，计算出的洪峰偏小，洪峰误差达-17%左右。

5 结 语

本文依据自由水蓄水容量(SM)与壤中水径流(RI)的物理意义建立这两个参数的函数关系，并在流域出口处利用实测流量过程线来划分水源，得到壤中水径流(RI)。利用SM和RI之间的函数关系估算得到出分水源参数SM、KI与KG的值。使得估算出来的SM、KI与KG的值更加合理准确。同时在构建新安江模型时，减少了所需要率定的参数的个数，使得参数率定的过程变得更加简便，提高了计算效率。

本文以陈河流域为研究示例，以该流域自由水蓄水容量与壤中水径流的函数关系为基础，采用2012080313号，2008090319号和2010092218号洪水资料对陈河流域的分水源参数进行估算，得到陈河流域的SM为9.99、KI为0.47、KG为0.23。同时将这些参数带入新安江模型对陈河流域上的17场洪水进行模拟演算，并取得了良好演算结果。

在实际的生产应用中应结合流域的自然地理气候条件，尽量将本方法应用于湿润流域以及半湿润流域。同时为进一步提高估算出来的参数的准确性，在应用时建议采用多场单峰式洪水资料对于分水源参数进行综合估算，以避免偶然误差的出现。

□

[1] 王佩兰,赵人俊. 新安江模型(三水源)参数的检验[J]. 河海大学学报，1989,17(4):16-20.

[2] 赵人俊,王佩兰,胡凤彬. 新安江模型的根据及模型参数与自然条件的关系[J]. 河海大学学报，1992,20(1):52-59.

[3] 王光生,周记华. 新安江模型改进的尝试[J]. 水文，1998,(S1):22-27.

[4] 郝庆庆,陈 喜. 新安江模型在乌江独木河流域的应用与改进[J]. 河海大学学报(自然科学版)，2012,40(1):119-112.

[5] 李致家,孔祥光, 张初旺. 对新安江模型的改进[J]. 水文，1998,(4):18-23.

[6] 芮孝芳. 水文学原理[M]. 1版，北京：中国水利水电出版社， 2004:280-287.

[7] 陈洋波,朱德华. 小流域洪水预报新安江模型参数优选方法及应用研究[J]. 中山大学学报(自然科学版)，2005,44(3):93-96.

[8] 李巧玲，王荣克，董小涛，等. 泾河上游植被覆盖动态及其与降雨径流的关系[J].水力发电，2015,(11):21-33.

[9] 姚 成，孙如飞，李致家，等. 下垫面变化条件下合河流域设计洪水修订[J].水力发电，2015,41(11):9-13.

[10] 安 东，李致家. 数据驱动模型与概念性模型的应用对比[J]. 水力发电, 2013,39(12):9-12.

[11] Yao Cheng. Improving the flood prediction capability of the Xinanjiang model in ungauged nested catchments by coupling it with the geomorphologic instantaneous uint hydrograph[J]. Journal of Hydrology, 2014,51(7):1 035-1 048.

[12] 吴险峰,刘昌明. 流域水文模型研究的若干进展[J] 地理科学进展, 2002,21(4):341-347.

[13] Hapuarachchi H A P, 李致家, 王寿辉. SCE-UA方法在新安江模型参数优化中的应用(英文)[J] 湖泊科学, 2001,12(4):305-314.