水资源开发影响下三江平原生态系统健康评价

刘 莹，王立权，孔 达，王子龙

(1.黑龙江大学水利电力学院，哈尔滨 150080；2.东北农业大学水利与土木工程学院，哈尔滨 150030)

0 引 言

生态系统健康是指在生态系统基本单元、区域或景观以及全球等多个尺度上生态系统的自我保持与更新的能力和社会经济服务功能[1]。随着社会经济的快速发展，人类高强度活动导致的生存环境恶化、水土资源萎缩、生态功能退化、承载能力降低、生物多样性缩减等生态系统问题日益突出，由此给社会经济可持续性发展带来了严重影响。生态系统健康日益受到国际社会的广泛关注，成为了生态系统管理的重要问题和热点领域[2]。生态系统健康评价兴起于20世纪80年代，在区域或景观尺度上已经开展了河流[3]、湖泊[4]、森林[5]、湿地[6]、流域[7]、海岛[8]、城市[9]等多种类型区域的生态系统健康评价，由简单到复杂、由定性到定量、由关注生物指标到重视服务功能，已成为该领域研究的重要趋势。

三江平原是三江(松花江、黑龙江和乌苏里江)汇流、冲积形成的沼泽化低平原，地理位置位于黑龙江省东部区域，行政区划包括佳木斯市、鹤岗市、双鸭山市、七台河市、鸡西市、穆棱市、依兰县，同时包括分布其中的几十个国有农场和林业局[10]。该区域经过几十年的开发，生态系统受到了一定的影响，特别是以地下水过度利用为代表的水循环变化引起的生态环境效应凸显，有必要定量评估三江平原的生态系统健康状况。

1 评价指标体系的构建

评价指标体系的构建是生态系统健康综合评价的基础和核心，不同研究中提出了多种生态系统健康综合评价指标体系的框架或方案[11-15]。针对三江平原生态系统特征，借鉴其他学者相关研究成果[16-18]，依据评价指标体系建立的原则，从社会、经济、生态3个子系统相互依存和相互作用的关系入手，注重生态系统的服务功能和价值，构建了三江平原生态系统健康评价指标体系包含目标层、系统层和指标层三个层次，如图1所示。

第一层为目标层(三江平原生态系统健康A)，为本研究所追求的总目标；第二层为系统层，是与此研究目标紧密联系的三个系统，即生态系统B1、社会系统B2、经济系统B3；第三层为目标层，共包括12项指标，各指标的计算公式及指标表征含义见表1。

图1 三江平原生态系统健康评价指标体系

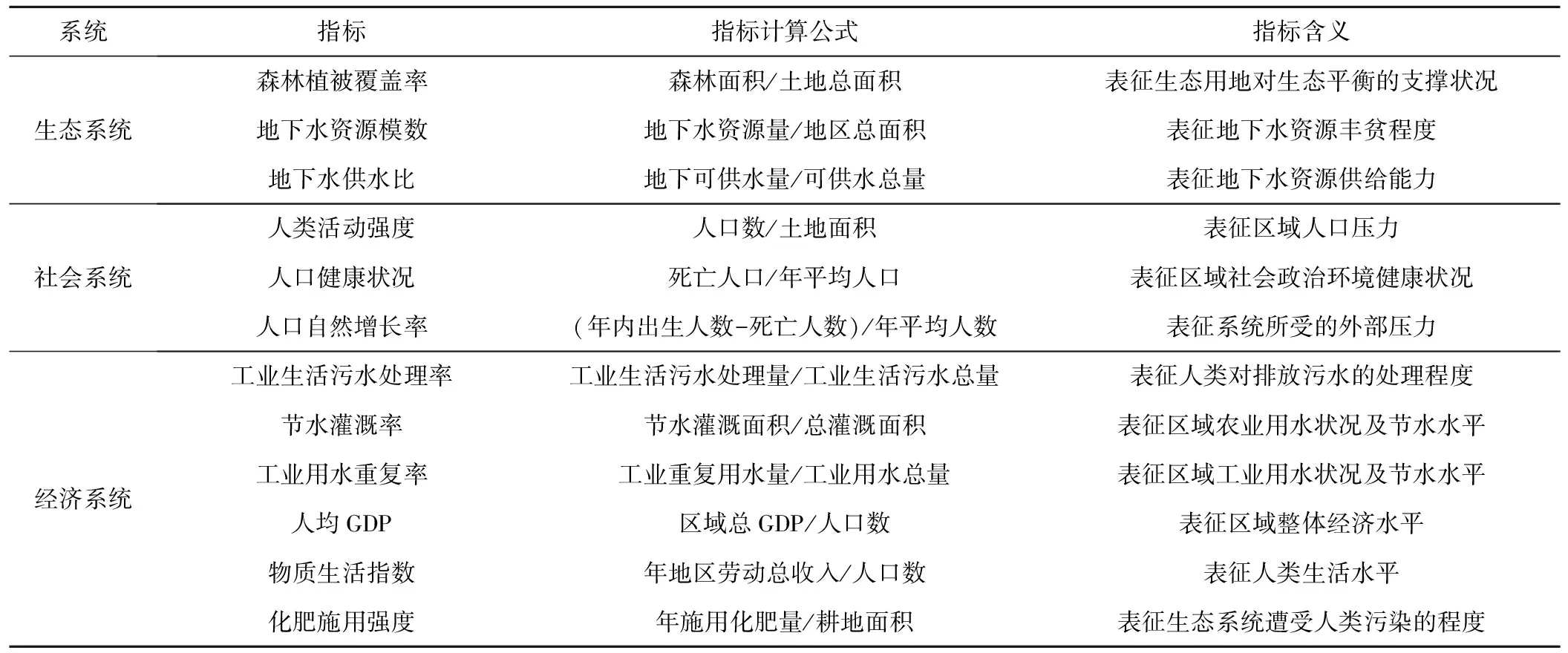
表1 三江平原生态系统健康评价指标计算公式及其含义

2 生态系统健康评价方法

生态系统健康评价的模型方法所采用的指标体系法，通过指标层次和指标选取体现待评价生态系统的特点与价值，能够更为全面地体现复杂生态系统健康状况[19]，本研究采用指标体系法，构建生态系统健康评价的指标体系，运用数学模型对三江平原生态系统健康进行综合评价。

2.1 粒子群优化算法

粒子群优化(Particle Swarm Optimization，简称PSO)算法是一种源于对鸟群捕食行为的研究而发明的进化计算技术[20]。粒子群体中的每个粒子代表解空间中一个可能的解，群体中每个粒子在优化过程中所找到的最好位置就是该粒子本身所找到的最好解，整个粒子群体所找到的最好位置就是整个粒子群体目前找到的最好解。前者称为个体极值，后者称为全局极值，每个粒子都通过这两个极值不断更新自己位置和速度，从而产生新一代粒子群体，在整个过程中粒子群体对解空间进行全面搜索寻找最优[21]。

2.2 基于粒子群优化的投影寻踪模型

运用投影寻踪模型开展评价问题研究的基本步骤是：根据数据结构寻找最佳投影方向，运用投影值计算公式，计算被评价对象各样本的最佳投影值，将各样本的最佳投影值进行相对比较，以确定待评价样本的优劣。对于投影寻踪模型而言，如何获得最佳投影方向是评价模型构建的核心问题，最佳投影方向的寻求可以通过一个复杂的非线性优化问题来解决[22]。本研究采用操作相对简单的粒子群算法优化最佳投影方向，建立投影寻踪评价模型[23]。

3 结果与分析

3.1 三江平原不同时期生态系统健康变化分析

采用粒子群优化算法对投影寻踪评价模型中的投影方向进行优化。利用MATLAB软件编制基于粒子群优化的投影寻踪评价模型程序，其中粒子群优化算法的参数设置如下：种群规模N=400，最大迭代次数Gmax=30，惯性权重w=0.996 5，学习因子c1=c2=2。在MATLAB环境下运行程序，得到投影指标函数最大值Q*(a)、最佳投影方向a*以及粒子群优化算法的迭代寻优过程，如图2所示。

图2 粒子群优化算法的寻优过程(三江平原)

采用2000-2011期间12年的数据，在MATLAB环境下运行程序，得出投影指标函数最大值Q*(a)=0.067 205 862 065 981，最佳投影方向a*=(0.727 930 300 198 792，0.001 433 060 959 954，0.287 577 467 128 917，0.622 426 401 101 767)。将最佳投影方向 代入公式即可得评价指标的最佳值a*=(1.431 847 331 635 9，1.600 378 867 016 74，1.594 041 503 740 58，1.393 663 791 829 91，1.393 663 537 376 41，1.32711440223315，1.393 667 335 629 2，1.254 983 159 846 58，1.155 477 796 397 66，1.263 885 522 669 75，1.091 869 707 395 63，1.011 533 228 609 15)。

计算可得三江平原地区2000-2011年12年的最佳投影值，如图3所示。由图3可知，2000-2011年，三江平原生态健康指数处于递减趋势，也就是说该期间待评价地区的生态健康情况处于下滑阶段。

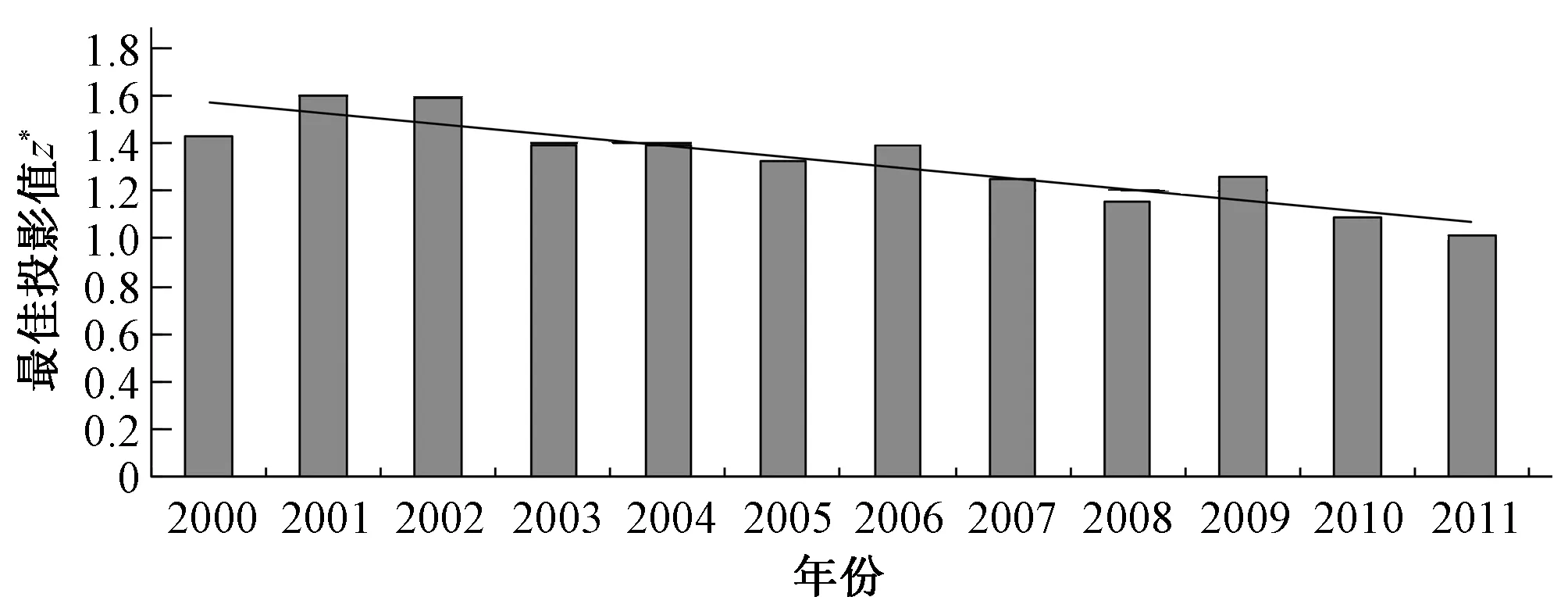
图3 2000-2011年三江平原生态系统健康指数

分析三江平原生态系统健康评价的12年结果可知，地下水资源模数由2000年的8.81 万m3/(km2·a)逐步下降至2011年的5.00 万m3/(km2·a)，而地下水供水比趋于稳定，所以地下水资源的压力越来越大，对三江平原生态系统健康有逆向影响。而此阶段大力发展工业及相关行业，使人均GDP得到了迅猛发展，由2000年的6 440.97 元/人增加到2011年的30 247.17 元/人，说明经济发展水平、人民的生活质量得到了提高，对水利的投入提供了保障。但同时，工业的发展也对三江平原生态系统的生态功能、物种的多样性、水质的标准起到了恶化的效果。

3.2 三江平原不同地区生态系统健康对比分析

根据前述评价模型的理论和方法，分别对2006年和2011年三江平原各地区生态健康状况进行评价。运行程序语言，计算投影指标函数最大值为Q*(a)=0.252 847 734 301 184，最佳投影方向a*=(0.002 922 068 891 988，0.485 527 633 730 488，0.840 718 624 038 648，0.016 525 437 155 085，0.000 381 150 453 593，0.000 074 440 839 243，0.136 551 761 430 636，0.196 282 829 488 327)，并得到粒子群优化算法的迭代寻优过程，如图4所示。

图4 粒子群优化算法的寻优过程(三江平原不同地区)

依据粒子群优化算法获得的最佳投影方向计算可得2006年和2011年评价指标数据集的最佳投影值，如图5、图6所示。

图5 2006年三江平原不同地区生态系统健康状况

图6 2011年三江平原不同地区生态系统健康状况

由图5可知，2006年穆棱市的生态系统健康状况处于三江平原平均水平之上，依兰县次之，佳木斯市、鸡西市、鹤岗市、双鸭山、七台河市六个地区生态健康状况处于三江平原平均水平，其中，穆棱市生态系统健康状况最优，双鸭山市生态系统健康状况最差。

对比分析图5与图6，自2006-2011年，三江平原区域内的依兰县、穆棱市、佳木斯市、鸡西市、鹤岗市、双鸭山市、七台河市生态系统健康状况均处于下滑状态，即三江平原生态健康状况持续恶化。对比分析各指标数据，相对于2006年，虽然2011年三江平原各地区的人均GDP等各项正向指标有所上升，但是2011年三江平原各地区的地下水供水比、人类活动强度、人口健康状况等逆向指标上升幅度更为明显，表明人类活动对生态系统健康的影响很大。

4 结 语

随着三江平原各地区经济的快速发展和人口数量的增多，水资源需求量会日益增加，对生态环境的污染 日益加剧，湿地面积不断减小。因此，应尽快提高水资源利用率，在加快经济的发展的同时，力争做到社会-经济-生态的和谐与可持续发展是保持三江平原生态系统健康发展的必要措施。

[1] Rapport D J, Costanza R, McMichael A J. Assessing ecosystem health [J]. Trends in Ecology & Evolution, 1998,13(10):397-402.

[2] Wang R S. Integrative eco-management for resource, environment and industrial transformation [J]. Systems Engineering-theory & Practice, 2003,(2):125-132.

[3] 朱卫红, 曹光兰, 李 莹, 等. 图们江流域河流生态系统健康评价[J]. 生态学报, 2014,34(14):3 969-3 977.

[4] 张艳会, 杨桂山, 万荣荣. 湖泊水生态系统健康评价指标研究[J]. 资源科学, 2014,36(6):1 306-1 315.

[5] 袁 菲, 张星耀, 梁 军. 基于干扰的汪清林区森林生态系统健康评价[J]. 生态学报, 2013,33(12):3 722-3 731.

[6] 郝文渊, 李文博, 王忠斌, 等. 西藏拉萨河谷拉鲁湿地生态系统健康评价[J]. 干旱区资源与环境, 2013,27(5):95-99.

[7] 廖静秋, 曹晓峰, 汪 杰, 等. 基于化学与生物复合指标的流域水生态系统健康评价----以滇池为例[J]. 环境科学学报, 2014,34(7):1 845-1 852.

[8] 陆丽珍, 詹远增, 叶艳妹, 等. 基于土地利用空间格局的区域生态系统健康评价----以舟山岛为例[J]. 生态学报, 2010,30(1):245-252.

[9] 赵 帅, 柴立和, 李鹏飞, 等. 城市生态系统健康评价新模型及应用----以天津市为例[J]. 环境科学学报, 2013,33(4):1 173-1 179.

[10] 何 琏. 中国三江平原[M]. 哈尔滨: 黑龙江科学技术出版社, 2000.

[11] 刘明华, 董贵华. RS和GIS支持下的秦皇岛地区生态系统健康评价[J]. 地理研究, 2006,25(5):930-938.

[12] 崔保山, 杨志峰. 湿地生态系统健康评价指标体系Ⅱ.方法与案例[J]. 生态学报, 2002,22(8):1 231-1 239.

[13] 陈 铭, 张树清, 王志强, 等. 基于GIS的蛟流河流域湿地生态系统健康评价[J]. 山东农业大学学报自然科学版, 2007,22(1):165-168.

[14] 戴全厚, 刘国彬, 田均良, 等. 侵蚀环境小流域生态经济系统健康定量评价[J]. 生态学报, 2006,26(7):2 219-2 228.

[15] 官冬杰, 苏维词. 城市生态系统健康评价方法及其应用研究[J]. 环境科学学报, 2006,26(10):1 716-1 722.

[16] 王慧亮, 王学雷, 莫明浩, 等. 基于生态健康的洪湖湿地恢复评价[J]. 武汉大学学报(理学版), 2010,56(5):557-563.

[17] 王文杰, 张 哲, 王 维, 等. 流域生态健康评价框架及其评价方法体系研究(一)----框架和指标体系[J]. 环境工程技术学报, 2012,2(4):271-277.

[18] 李春晖, 郑小康, 崔 嵬, 等. 衡水湖流域生态系统健康评价[J]. 地理研究, 2008,27(3):565-573.

[19] 马克明, 孔红梅, 关文彬, 等. 生态系统健康评价:方法与方向[J]. 生态学报, 2001,21(12):2 106-2 116.

[20] Kennedy J, Eberhart R. Particle swarm optimization[C]∥ IEEE International Conference on Neural Networks, 1995. Proceedings. IEEE, 1995:1942-1948 vol.4.

[21] 雷崇民, 任再敏, 高岳林. 约束优化问题带有混沌变异的PSO-DE混合算法[J]. 兰州理工大学学报, 2010,36(6):94-98.

[22] 陈广洲, 汪家权. 基于模拟退火算法的投影寻踪方向优化[J]. 合肥工业大学学报(自然科学版), 2008,31(8):1 315-1 317.

[23] 蔡怡馨, 王 静, 刘鹏玲,等. 利用组合模型评价云南省水资源利用效率[J]. 人民黄河, 2015,37(5):58-61.