砂土斥水性与含水率关系的试验研究及理想模型分析
刘 畅,陈俊英,2,张智韬,2,柴红阳,蔡耀辉
(1.西北农林科技大学水利与建筑工程学院,陕西 杨凌 712100;2.西北农林科技大学旱区节水农业研究院,陕西 杨凌 712100)
0 引 言
土壤斥水性是一种土壤颗粒表面不能或难以被水湿润的物理现象[1]。土壤斥水性改变了土壤的渗透性能,降低土壤入渗和保水能力,对土壤水分运移、水土保持和地下水环境产生严重影响[2]。
土壤含水率作为土壤斥水性最重要的影响因素之一,受到国内外学者的广泛研究。随着土壤水分含量的变化,土壤斥水程度发生较大改变。Bond等[3]发现土壤斥水性随着含水率提高而逐渐减小,最后消失的现象;Dekker等[4]研究了荷兰的斥水性砂土,发现土壤含水率小于2%时,斥水性消失;King等[4]研究发现土壤斥水性的临界含水率范围是34%~38%;张培培等[5]试验得出土壤斥水性随含水率变化的趋势为双峰曲线;而陈俊英等[6]通过不同类型斥水土壤的试验研究,得出斥水性随含水率提高呈现单峰曲线变化趋势。这些研究均是对滴水渗透时间法试验测定结果的趋势规律进行总结,而缺少理论的数量分析。
土壤斥水性随含水率的变化,反映了不同含水率下土壤水吸力的差异,但受到土壤质地结构的影响难以直接定量分析,而通过理想土壤颗粒物理模型下接触角变化进行理论分析可以提供方便。栾茂田等[7]通过理想土壤颗粒模型,提出等效基质吸力和广义土壤水分水特征曲线的概念。Lechman等[8]、杨松等[9]基于理想土壤颗粒模型,计算分析了不同接触角下土壤水吸力和含水量的关系。张昭等[10]通过不等径土颗粒模型,分析了不同表面粗糙程度下土颗粒与液桥相互作用的微观水力特性。这些研究主要基于理想土壤颗粒模型,通过接触角的变化对土体的强度特征和形变特性等进行分析,较多的应用于岩土力学方向,而在土壤的亲斥水性质方面的研究和涉及相对较少。
本文通过试验观测和基于理想土壤颗粒模型分析相结合的方式,从滴水渗透时间法和接触角法两种斥水性表示方法分析了砂土斥水性随土壤含水率的变化规律,对比了不同砂土自身斥水强度对土壤斥水性的峰值和阈值及其对应含水率高低的影响,解释了滴水渗透时间法和接触角法在土壤斥水性表达上的差异和联系。
1 材料与方法
1.1 土壤斥水性的表示方法
滴水渗透时间(WDPT)法是当WDPT>5 s时,认为土壤具有斥水性质[3],Dekker和Ritsema[11]根据WDPT值的大小将土壤斥水程度划分5个等级:当5 s
接触角(CA)法是测定土表的固体、液滴和空气三相体系交点处的气-液界面切线和固-液界面线之间夹角δ(0<δ<180°)的大小评价土壤的斥水性[12](图1)。δ的大小受液滴分子之间内聚力与固体和液滴之间附着力的相对大小影响[7]。图1中γSG、γSL和γLG分别表示固-气、液-固和液-气界面张力,当δ<90°时,γSG>γSL,液滴沿固体表面铺展,并使其润湿,表现出亲水性质。随着δ增大,亲水性质逐渐减弱。当δ>90°时,γSG<γSL,液滴在固体表面收缩聚集成珠球状,固体表面很难被润湿,表现出斥水性质。
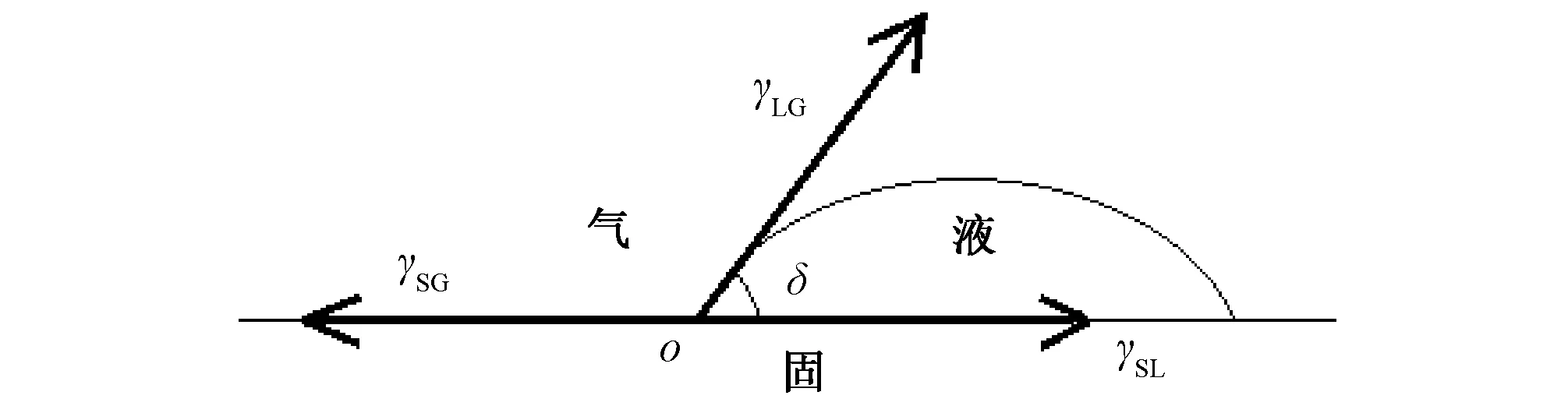
图1 液滴在固体表面的接触角Fig.1 Contact angle of droplet on solid surface
1.2 供试土样性质及其改性处理
试验土样选用砂土,取自0~30 cm的表层土壤,将土壤自然风干、碾压粉碎,过2 mm筛网进行后续试验,通过激光粒度仪测定土样颗粒组成(表1)。采集土壤表现为亲水性质,需对土壤进行改性处理,获得具有斥水性的砂土。该改性处理仅改变砂土颗粒表面性质,不改变土壤结构。改性方法有物理和化学方法,本试验通过向土壤中添加表面活性材料(十八烷基伯胺,C18H39N)的方法获得斥水性砂土[13,14]:分别按1 kg风干砂土添加0.1、0.2、0.4 g表面活性材料的比例,再加入适量水充分混合均匀,放置24 h,配制出不同斥水程度的斥水砂土,分别记为S1、S2、S3。通过透过测量法和Washburn方程[15],确定土样S1、S2、S3以及未经改性处理的砂土S0的接触角分别为18.7°、43.3°、61.2°和3.8°。
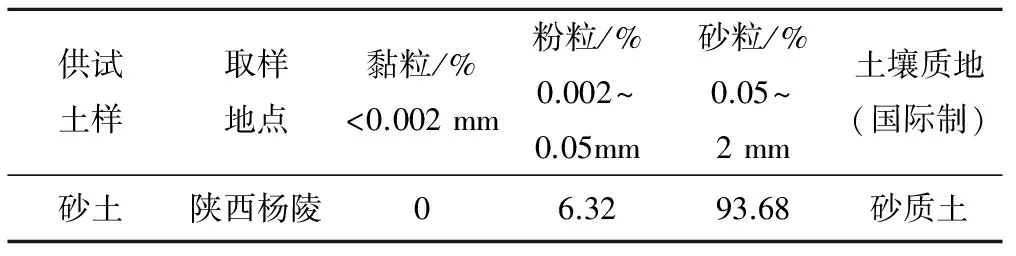
表1 试验砂土的物理性质Tab.1 Physical properties of the test sand
1.3 试验方法和观测内容
将斥水性砂土S1、S2、S3分别装入试验土盒中,土盒由10 mm厚有机玻璃材料制成,尺寸为200 mm×200 mm×100 mm(长×宽×高),土盒底面有16个直径2 mm的小孔,装土前在土盒底部铺设滤纸,装土高度为80 mm。通过气压式喷壶模拟田间喷灌的灌水方式,向土盒中缓慢均匀喷洒水雾,直至土盒底部有水流出,达到土壤的最大持水量,停止喷水。将各试验土盒放置在避光的实验室进行水分自然蒸发,实验室内温度保持在20 ℃,避免风和温度变化等因素对试验结果造成潜在影响[6]。在砂土水分蒸发脱湿过程中,每间隔一段时间,测定一次砂土的斥水持续时间及其对应的土壤含水率,直至蒸发到含水率不再变化,停止测量。
采用WDPT法测定斥水性砂土S1、S2、S3的斥水持续时间:选用同一标准的滴管,分别在距离砂土S1、S2、S3表面5 mm的不同位置处,垂直滴下10滴蒸馏水,使用秒表记录每个水滴在砂土表面渗入土壤需要的时间,计算10滴水入渗时间的平均值作为每个土样最终的斥水持续时间[2,6]。随着斥水性砂土的蒸发脱湿,土壤含水率逐渐减小,在进行土壤斥水持续时间测定时,相应的取砂土表层0~10 mm 范围内约20 g土壤,采用105 ℃烘干法测定土壤的质量含水率。取土时应该避开滴水的位置,避免水滴入渗改变了土壤含水率。
2 结果与分析
2.1 试验结果
图2为不同含水率下的各土样的斥水持续时间,其变化趋势符合陈俊英等[6]得出的斥水持续时间与含水率之间满足的Lorentzian曲线关系。随着水分蒸发、土壤脱湿,3个不同斥水程度砂土的WDPT均表现为逐渐增大的变化趋势,当土壤含水率降低到某一特定含水率值时,砂土S1、S2、S3的WDPT都达到极大值,而随着土壤含水率的进一步降低,各个土样的WDPT开始逐渐减小。当土样的WDPT达到峰值时,对应的土壤含水率都在1.5%~2%范围内。即在一定土壤含水率变化范围内,随着土壤含水率的提高,砂土S1、S2、S3的斥水性均呈现出以含水率1.5%~2%为拐点的先增强、后减弱的单峰曲线变化趋势。
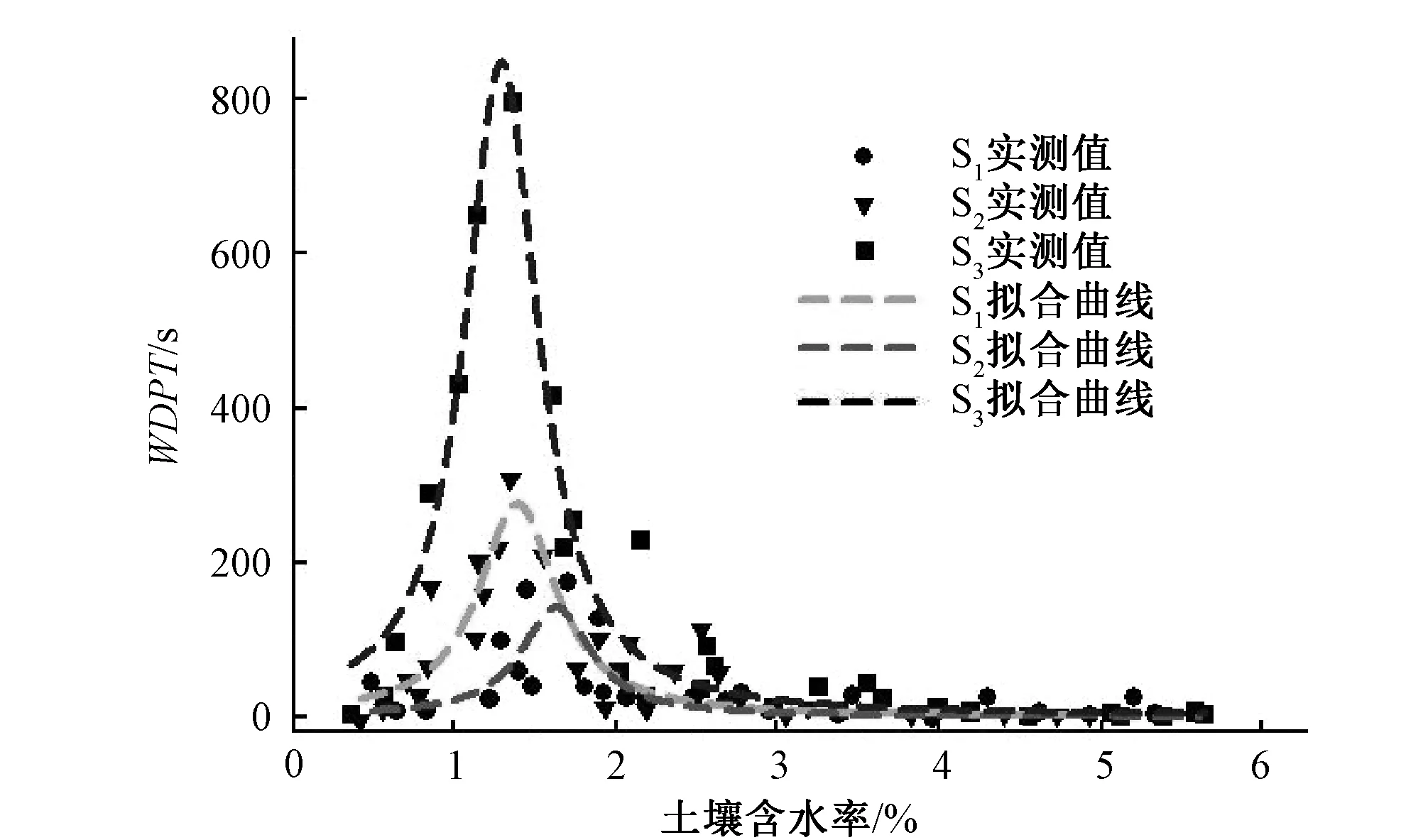
图2 滴水穿透时间与土壤含水率的关系Fig.2 Relationship between WDPT and soil moisture content
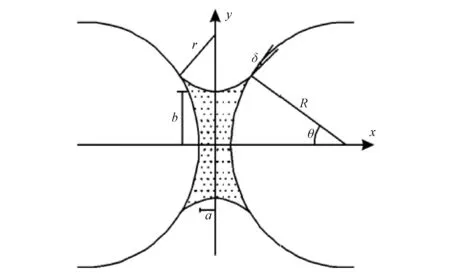
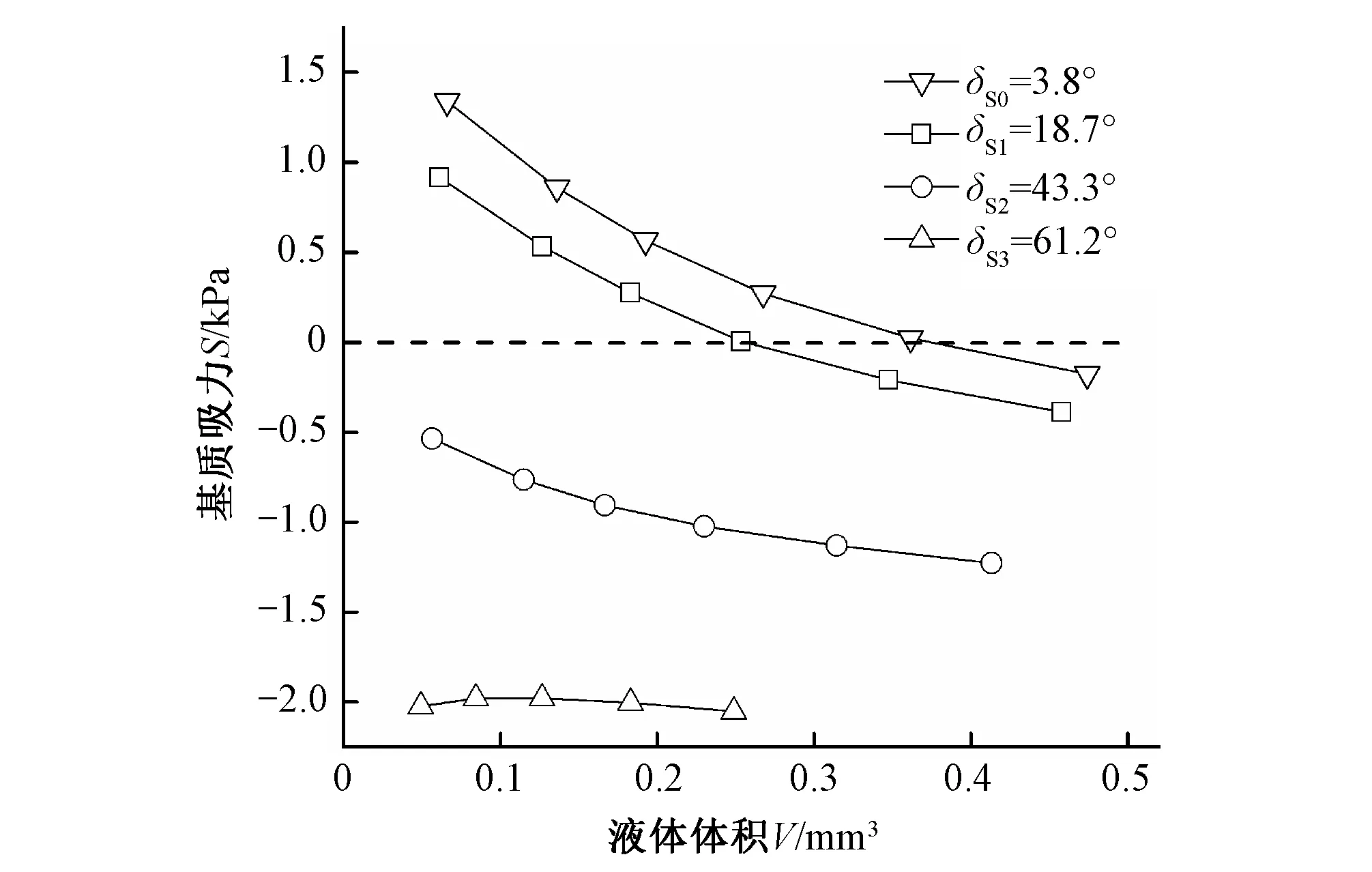
由图2可知,虽然S1、S2、S3三个斥水程度的砂土随着土壤含水率的变化趋势基本一致,但是不同的表面活性材料掺量,导致在相同土壤含水率时各个土样的WDPT差异很大,整体表现为S1 2.2.1 理想模型建立 真实的土颗粒三维方向尺寸差异很大,多为不规则形状。以当量粒径代替其真实直径,将土壤颗粒近似看作理想的球体颗粒[7-10],假设土壤颗粒半径均为R,土壤颗粒之间的距离为M=2a(图3)。当土壤含水率较低时,土壤颗粒之间由水量很少的液桥相互连接(重力可忽略不计),液桥的弯液面满足热力学的一般假设,为圆弧形状。在图3所示的xoy平面内,土壤颗粒的圆心距离为L=2(a+R),弯液面的形状是半径为r的一段圆弧,弯液面底部的高度为b,水与土壤颗粒的接触角为δ,土壤颗粒的半湿润角为θ。 图3 理想砂土颗粒的平面模型Fig.3 Plane model of ideal sand particle 在土壤颗粒与弯液面交点处,满足: (x-a-R)2+y2=R2 (1) x2+(y-r-b)2=r2 (2) 由式(2)可得出土壤颗粒与弯液面交点处的弯液面切线斜率为: (3) 2.2.2 液桥体积和基质吸力的表示 土壤颗粒之间液体体积V的大小,在一定程度上可以反映土壤的饱和程度,即V越大,土壤的含水率越高。两个土壤颗粒之间液桥的体积可由弯液面圆弧绕两球心轴线旋转得到: (4) 含水率较低(水分自身重力不计)的不饱和土壤基质吸力S主要受到孔隙气压力Sa和孔隙水压力Sw影响。土体颗粒间液桥受到液体表面张力作用,在弯液面内外产生压力差△P,数值上与基质吸力S是相反数。其关系可用Laplace公式表示: (5) 式中:σ为液体表面张力系数;R1、R2为曲率半径。图3所示弯液面情况R1=r、R2=-b,则有: (6) 当接触角δ增大时,基质吸力S减小,土壤亲水性质逐渐减弱。当δ增大到一定程度时,S值小于0,此时土壤对水分表现出排斥作用,斥水性质增强。在接触角δ变化时,理想土壤颗粒模型的各参数也随之改变,由式(1)、式(2)、式(3)联立确定,进而求得液桥体积V[式(4)]。 2.2.3 基质吸力与液桥体积的关系 假设土壤颗粒的半径R=1 mm,土壤颗粒的间距M=2a=0.2 mm,查表得到20 ℃时水的表面张力系数为72.8 kN/m。已知砂土S0、S1、S2、S3的接触角分别是3.8°、18.7°、43.3°和61.2°。对于给定不同的弯液面底部高度b,可以计算得到相应的弯液面半径r,进而求解出基质吸力S和液桥的体积V,二者关系如图4所示。 图4 基质吸力与液桥体积的关系Fig.4 Relationship between matric suction and liquid bridge volume 由图4不同接触角δ下土体颗粒间基质吸力S和液桥体积V的关系可知,当接触角δ相同时,基质吸力S随着液桥体积V的增大呈现出逐渐减小的变化趋势,表现为土壤的亲水性质逐渐减弱,当液桥体积V增加到一定程度时,基质吸力S<0,此时土体颗粒开始对水产生排斥作用,表现出斥水性质;当液桥体积V相同时,基质吸力S随着接触角δ的增大而逐渐减小,直到基质吸力S<0时,表现出对水分的斥力;而当基质吸力S=0时,随着接触角δ的增大,液桥体积V逐渐减小,土壤饱和度相对降低。所以在一定土壤含水率变化范围内,3个土样的WDPT随含水率提高而逐渐增大;而随着土样斥水强度的提高,WDPT峰值增大,且表现出斥水性质的阈值和WDPT峰值对应的土壤含水率逐渐减小。 由图2和图4可以看出,WDPT法的试验结果和基于理想土壤颗粒模型下接触角变化的理论分析结果存在差异:图2所示的变化关系中,随着土壤含水率提高,各土样WDPT曲线均在峰值处出现拐点,即斥力增大到一定程度后,随着土壤含水率继续提高开始逐渐减小。而图4所示变化关系中,虽然基质吸力S随着液桥体积V提高而减小的趋势逐渐减弱,但是没有出现V增大到一定程度后,S逐渐增大的情况。其原因可能是在图3的理想土体颗粒模型中,假定不饱和土壤的含水率较低,液桥水分含量相对很少,分析计算过程中忽略了液桥水分的自身重力影响。而随着土壤含水率的提升,土壤颗粒间的液桥体积必然增大,所含水分的质量提高,此时水分的自身重力影响较大,不能忽略。同时图2所示WDPT法测得土样的下阈值含水率(WDPT峰值拐点之前)的相对大小关系为θS3<θS2<θS1,但其上含水率阈值(WDPT峰值拐点后)的相对大小关系并不明显,而由图4理想土壤颗粒模型下的基质吸力S与液桥体积V的变化关系也无法判断。同样是由于土壤含水率的增大,使其自身重力影响加大。在各土壤含水率下,基质势、重力势和土样表现出的不同斥水程度等共同作用,使得各个土样的上含水率阈值相对大小难以确定。 WDPT法和接触角法对同一斥水性砂土的评价出现矛盾:通过添加不同质量表面活性斥水材料进行改性处理获得斥水性砂土S1、S2、S3的接触角分别为18.7°、43.3°和61.2°,均小于90°,土壤仍应表现亲水性质。但通过WDPT法测得土样S1、S2、S3的WDPT值均随着土壤含水率的增大而提高(峰值拐点前),并从某一含水率开始大于5 s,表现出斥水性质,导致两种方法对于试验砂土斥水性的评价产生差异。这主要因为WDPT法和接触角法是不同的土壤斥水性评价方法,WDPT法主要是评价土壤的斥水持久性,而接触角法是评价土壤的斥水强度[15]。对于WDPT法,认为土壤的WDPT>5 s时,即表现出具有斥水性,并且按照WDPT值的大小划分不同等级,其实质是对土壤斥水性质的持续性大小进行描述。而接触角法是通过测定土表的固、液、气三相接触角δ的大小判断土壤亲水或斥水的相对强弱程度,并规定δ=90°是土壤表现出亲水和斥水的接触角分界。因此,虽然本试验中的砂土土样S1、S2、S3的接触角均小于90°,但随着接触角增大,砂土的亲水程度逐渐减弱,潜在的斥水性质逐渐表现出来,在相同含水率下对应的WDPT值也逐渐提高(图2),此时土壤表现出一种临界状态的相对斥水(或相对亲水)特征[16],所以两种方法的结果并不矛盾。 本文通过对斥水砂土进行试验探究和基于理想土壤颗粒模型的对比分析,得出以下结论。 (1)各个斥水程度砂土随含水率变化的趋势大体一致:随着土壤含水率的提高,砂土斥水性呈现出以1.5%~2%含水率范围为拐点的先增大、后减小的单峰曲线变化趋势。 (2)砂土自身潜在的斥水强度对其斥水性表达影响较大。在1.5%~2%含水率范围内,随着砂土自身斥水强度的提高,WDPT峰值的数值逐渐增大,且峰值对应的含水率值逐渐减小。同时砂土斥水性的下阈值含水率也逐渐减小,但上阈值含水率的相对大小趋势并不明显。 (3)接触角法与WDPT法对土壤斥水性质的评价虽然存在一定差异,但实质上并不矛盾,主要是两种方法的评价指标不同,接触角法评价的是土壤自身斥水强度,而WDPT法是评价土壤斥水的持久性,可根据实际情况选择适合的测定方法。 [1] 杨邦杰. 土壤斥水性引起的土地退化、调查方法与改良措施研究[J]. 环境科学,1994,15(4):88-90. [2] 李 毅,商艳玲,李振华,等. 土壤斥水性研究进展[J]. 农业机械学报,2012,43(1):68-75. [3] Bond R D, Harris J R. The influence of the microflora on the physical properties of soils. I. Effects associated with filamentous algae and fungi[J]. Australian Journal of Soil Research, 1964,2(1):111-122. [4] Dekker L W, Ritsema C J. Wetting patterns and moisture variability in water repellent Dutch soils[J]. Journal of Hydrology, 2000, s231-232(00):148-164. [5] 张培培,赵允格,王 媛,等. 黄土高原丘陵区生物结皮土壤斥水性[J]. 应用生态报,2014,25(3):657-663. [6] 陈俊英,吴普特,张智韬,等. 土壤斥水性对含水率的响应模型研究[J]. 农业机械学报,2012,43(1):63-68. [7] 栾茂田,李顺群,杨 庆. 非饱和土的理论土-水特征曲线[J]. 岩土工程学报,2005,27(6):611-615. [8] Lechman J, Lu N. Capillary Force and Water Retention between Two Uneven-Sized Particles[J]. Journal of Engineering Mechanics, 2008,134(5):374-384. [9] 杨 松,吴珺华,董红艳,等. 砂土和黏土的颗粒差异对土壤斥水性的影响[J]. 土壤学报,2016,53(2):421-426. [10] 张 昭,刘奉银,张国平,等. 不等径湿颗粒与液桥相互作用的微观水力特性[J]. 水利学报,2013,(7):810-817. [11] Dekker L W, Ritsema C J. How water moves in a water repellent sandy soil: 1. Potential and actual water repellency[J]. Water Resources Research, 1994,30(9):2 507-2 517. [12] Dekker L W, Jungerius P D. Water repellency in the dunes with special reference to The Netherlands[J]. Catena, Supplement, 1990,(18):173-183. [13] 刘春成,李 毅,郭丽俊,等. 微咸水灌溉对斥水土壤水盐运移的影响[J]. 农业工程学报,2011,27(8):39-45. [14] 李 毅. 斥水土壤水盐运移规律及空间变异性研究[M]. 北京:中国水利水电出版社,2016. [15] 储 鸿,崔正刚. 粉体接触角的测定方法[J]. 化工时刊,2004,18(10):44-47. [16] Ellerbrock R H, Gerke H H, Bachmann J, et al. Composition of Organic Matter Fractions for Explaining Wettability of Three Forest Soils[J]. Soil Science Society of America Journal, 2005,69(1):57-66.2.2 基于理想模型从接触角分析斥水性和含水率关系
3 讨 论
3.1 土壤含水率对斥水性的影响
3.2 接触角法与WDPT法对斥水性评价的差异和联系
4 结 语

