出水管角度对网式过滤器内部流场影响研究

陶洪飞，滕晓静，马英杰，赵经华，洪 明，马 亮，付秋萍

(新疆农业大学水利与土木工程学院，乌鲁木齐 830052)

过滤器是微灌系统中的重要组成部分，网式过滤器具有结构简单、造价低廉、体积小等特点，一般作为最末级过滤器，其过滤性能好坏直接影响到下级输配水管网的正常运作和使用寿命。

国内对过滤器的研究虽起步较晚，但近些年已有一些系统的研究。石河子大学的宗全利[1,2]、骆秀萍[3,4]、刘飞[5]等人针对自清洗网式过滤器的水力性能进行了大量研究。山西省运城市水利科学研究所研发了一种离心筛网一体式过滤器[6]，将筛网置于离心过滤器腹腔中，并对该过滤器的水力性能[7]、砂砾运移规律[8]进行研究。在国外，Capra[9]研究了不同类型的过滤器对废水的过滤能力，结果表明网式过滤器和叠片过滤器对过滤有机污物的能力较差。Yurdem H[10]、Duran-Ros M[11]等人对过滤器的水利性能和效率进行了深入研究。

过滤器传统的研发过程是需要先制造出网式过滤器的实体模型，再进行水力性能和泥沙处理能力的研究，该研发方式不仅周期长，而且成本高，也无法探寻过滤器内部的流场状况。随着计算机普及以及计算软件的发展，关于网式过滤器数值模拟的研究也开始出现[12,13]。王新坤[14]用多孔介质模型模拟滤网，将数值计算结果与试验结果相比较，发现吻合程度较高，证实了多孔介质模型的可行性。目前，已有不少学者将多孔介质模型应用到其他型号的过滤器上，以探究过滤器内部流场状况并进行结构优化[15-18]。相对于传统过滤器的研发方式，将CFD技术应用于过滤器的结构优化有着无可比拟的优势。

本文拟利用Fluent软件模拟网式过滤器在过滤状态下的清水流场，探究出水管与罐体之间的角度对过滤器内部流场的影响，从而为网式过滤器的优化设计提供理论依据。

1 全自动网式过滤器的介绍

本文所研究的全自动网式过滤器(下文简称“过滤器”)具有便于维护、工作流量大、水头损失小、自动反冲洗等优点。该过滤器由罐体、不锈钢滤网、自动控制器等部件组成，图1为过滤器的整体示意图。过滤器主要尺寸如下：进水管、出水管直径均为0.2 m；排污管直径0.05 m；滤网长0.961 m，直径0.2 m；罐体长1.031 m，直径0.257 m。为过滤器建立坐标系，坐标原点在进水管中心处，滤网轴线、进水管轴线、排污管轴线均与X轴重合，出水管轴线平行于Y轴，出水管与罐体之间的角度α=90°。取Z=0 m断面为过滤器横断面。

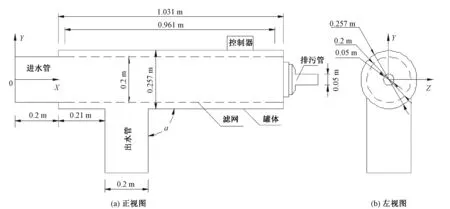
图1 全自动网式过滤器示意图Fig.1 Structural diagram of automatic screen filter

过滤器过滤时，排污阀处于关闭状态，粒径大于滤网孔径的固体杂质会被拦截在滤网内部，而净水在滤网外部。进水管口、出水管口装有压力传感器，当进、出水口压降达到预设压差时，控制器控制电磁阀打开排污阀，此时固体杂质从排污管排出，排污时间达到预设时间后，排污阀自动关闭，直冲洗结束。

2 全自动网式过滤器的数值模拟

2.1 三维建模

先用Gambit软件对过滤器进行前期建模及网格划分，再用Fluent软件对过滤器过滤状态进行数值模拟，最后利用Tecplot软件进行后期数据可视化处理。图2是过滤器的三维图，图中深颜色的部分为滤网。

图2 三维图Fig.2 Three-dimension graph

2.2 网格划分

由于过滤器模型为三维模型，故采用体网格划分更加便捷。其中进水管和排污管由于结构简单，采用六面体结构性网格；其余部分由于结构复杂，同时为了避免在Fluent软件中检查时网格出现负体积，采用四面体非结构网格。网格是后续计算的基础，网格的数量关系到计算量的大小和计算结果的准确性，为了探究网格节点间距(网格数量取决于网格节点间距)对计算结果的影响，针对本模型，划分了三种不同数量的网格，具体节点间距、网格数量如表1所示。

表1 网格划分Tab.1 Mesh generation

2.3 计算模型、边界条件及求解方法

数值模采用非定常流二阶隐式格式，以提高计算精度；湍流模型采用Realizablek-ε模型。

求解方法采用基于压力-速度修正算法(SIMPLE)；差分格式采用精度更高的二阶迎风格式；残差标准设置为1.0×10-3；为了尽快收敛，迭代时间步长为1.0×10-4s。

边界条件设置如下：①过滤器罐体按固壁处理。②本文仅模拟过滤状态下的流场，此时排污口关闭，故排污管出口视为固壁。③操作压力默认为101 325 Pa，故以下讨论的压强均为相对压强。④进口、出口的条件同物理实验，即进口为速度进口，流速为1.769 m/s(此时流量为200 m3/h)。出水管出口为压力出口，出口压强为263 kPa。⑤滤网采用多孔阶跃模型，即将滤网所在的面设为Porous Jump。有关多孔阶跃模型的具体设置见2.4节。

2.4 多孔阶跃模型

物理实验中，滤网孔径为0.18 mm，如此微小的网孔，若按照实际状况划分网格，必定会十分麻烦，且计算量巨大。借鉴其他学者对多孔阶跃模型的应用[14,16,19]，可以通过孔隙率、渗透率等参数体现滤网的阻力特性。将滤网所在面定义为多孔阶跃面，可以大大简化问题。多孔阶跃面(Porous Jump)是多孔介质(Porous Media)模型的一维简化，用以模拟速度-压降特性已知的薄膜。多孔介质模型定义在流体区域上，而多孔阶跃面定义在界面区上，相比多孔介质模型，多孔阶跃面更易收敛，更适合模拟滤网。

多孔介质模型通过在动量方程中增加黏性阻力项和惯性损失项这两个源项来模拟计算域中多孔性材料对流体的流动阻力。有关这两个源项可以参考文献[20]。ANSYS FLUENT参考手册给出了各方向黏性阻力系数和惯性损失系数计算公式：

(3)

式中：C1为阻力系数，m-2；k为渗透率，m2；C2为惯性损失系数，m-1；D为滤网孔直径，mm；ε为孔隙比，%。

为了便于比较，滤网有关参数设置与物理实验中所用滤网实际参数一致：滤网孔直径D=0.18 mm；孔隙比ε=38 %；丝径d=0.112 mm；滤网厚度取0.001 m。根据以上数据，可计算得到k=3.083 3×10-11m2，C1=3.24×1010m-2，C2=219 703.2 m-1。

2.5 模型验证

为了更好地比较，规定过滤器进口压强与出口压强之差为该过滤器的压降。将三种不同网格的计算结果同物理实验结果相比较。对比结果如表2所示。由表2可知，网格数量对计算结果有明显的影响。网格数越多，即网格密度越大，计算结果越准确。当网格数量为69 189个时，计算得到的压降与实际压降误差为12%，当网格数量为123 887个时，相对误差为6.77%。当网格数量为168 681时，相对误差仅为5.06%。当网格数量多到一定程度时，再增加网格数量，对提高计算精确度帮助不大。对比工况2、3，网格个数多了44 794个，相对误差却只减小了1.71%，可以看出工况2的网格密度已经足够。由此得出结论：工况1的网格数量不够，计算误差太大，不宜采用。工况2、3计算误差都在可接受范围内，但工况3网格数量太多，计算量太大，也不宜采用。故本模型采用工况2的网格节点间距较为合理。

表2 结果对比Tab.2 Results comparison

3 不同出水管角度的数值模拟

3.1 原模型流场分析

这里仅分析工况2(网格数量为123 887个)的计算结果。图3是过滤器横断面的速度云图、矢量图和压强云图。从图3(a)中可以看出水流均匀地从进水管进入滤网，一部分水流直接穿过滤网，流向出水管。而另一部分水流在滤网内部继续前行，与过滤器尾部折返回来的水流相互混掺，最后沿反方向流向出水管。进水管流速为设定的1.769 m/s，滤网进口段流速约为1.4 m/s，沿着滤网方向，流速逐渐变小，过滤器尾部流速很小，接近静止。出水管段Y字型高流速区是整个过滤器流速最大的区域，而就在高流速区域左右两侧各有一个低流速的漩涡区域，这是因为出水管垂直罐体，结构突变，水流在这块区域混掺和碰撞，从而消耗能量，流速减小。从速度矢量图上可以看出，出水管左侧流来的水流流速大于右侧的水流流速，且左侧漩涡区也大于右侧的漩涡区。进入出水管的水流流动方向由近似水平逐渐转变为垂直，在这个过程中，水流冲击出水管右侧边壁，造成能量损失。

图3 流场分析Fig.3 Flow field analysis

从图3(b)中可以看出，进水管、滤网、排污管内部压强分布均匀，且压强较大。以滤网为分界面，滤网外部的压强明显小于滤网内部，这正是由于多孔阶跃面产生的压降，反映到实际情况上，就是液体穿过滤网所产生的压降。在滤网前部压降约为6 kPa，滤网中部(即出水管上部)压降约为8 kPa，滤网尾部压降约为2 kPa。漩涡区域压力低于周围约为2 kPa。整个过滤器压强损失约为10 kPa，可见绝大部分压强损失在滤网附近。

3.2 不同出水管角度模型

由于这种过滤器具有实物的只有一种----出水管垂直罐体，即夹角α=90°。为研究其他夹角对过滤器内部流场的影响，本文采用相同的数值计算方法，对不同出水管夹角的过滤器进行数值模拟。在保证滤网面积、进水管直径、出水管直径、流量均不变的前提下，提出以下方案：由于出水管中水流方向与水平方向呈斜交状态，故可尝试逆时针旋转出水管，即改变图1中的夹角α值，分别模拟α=75°、60°、45°、30°时的流场。

3.3 不同模型计算结果

表3为不同出水管角度的计算结果。由表3可以看出，出水管与罐体夹角α对压降的影响非常小。当α=30°时，压降最小为0.997 m，当α=60°时，压降最大为1.051 m，两者相差仅为0.054 m。出水管角度对压降影响极小是因为滤网面积、孔径及滤网压降特性均未变化，而压降产生的主要部位是滤网，故夹角α的改变对压强损失的影响可忽略不计。

表3 数值模拟结果Tab.3 Numerical simulation results

图4为各个方案的速度云图和矢量图。从流场分布可以看出：①滤网内有一块低速回流区域(滤网尾部，靠近下侧滤网)，从滤网尾部一直延伸到出水管右侧边缘，在夹角α由75°变到30°的过程中，出水管与罐体相交的右侧交点逐渐向右边移动(左侧交点则向左边移动)，导致回流区域也跟着向右侧移动，回流区域面积变小。在回流区域前部，水流流向为正向，且流速分布均匀约为1.8 m/s，可见此处是滤网有效利用率最高的部位。在回流区域，流速较小，且流向各异，因此回流区域滤网的过滤效率较低。当夹角α=30°时，回流区域最小，滤网有效利用率最高。除此之外，进水管、排污管、滤网内部速度分布特征基本与夹角α=90°时一致。②出水管内流速分布有较大差异。随着夹角α逐渐变小，出水管内高流速区域面积先增大后减小，且位置也发生了较大变化。当夹角α=90°时[图3(a)]，高流速区域在出水管上部中间略微偏右的位置；当夹角α=75°时[图4(a)]，在出水管上部中间的位置；当夹角α=60°时，在出水管中下部左侧的位置；当夹角α=30°时，在出水管左下部的位置，且形状也不再是Y字型。③出水管内漩涡区也随着高流速区的改变而发生变化。当夹角α=90°时[图3(a)]，漩涡区在出水管左右两侧，左侧大于右侧。随着夹角α变小，出水管内左侧漩涡渐渐消失，而右侧漩涡却在变大。由于夹角α变小，出水管左侧水流能更平顺地进入出水管，因此左侧漩涡消失。出水管右侧水流为从过滤网尾部回流的水流，水流方向与出水管出流方向存在一个夹角，α越小该夹角越大，回流水需转过的角度也越大，因此在出水管右侧造成的漩涡也越大。值得注意的是，出水管左侧水流流速大、流量大，右侧水流流速小流量小，左侧水流占据主流。因此将出水管逆时针旋转，顺应主流是合理的。但是出水管右下部存在一个较大漩涡区同样不可忽略，对于消除这个漩涡区可以尝试将出水管向右平移，以进一步减小出水管右侧水流流量，达到减小漩涡的目的。

图4 断面速度场Fig.4 Velocity field of the section

图5为各个方案压强云图。与α=90°时的压强分布规律相比较，当夹角α改变时，进水管、排污管、罐体内压强分布仍然比较均匀，最大压差约为2 kPa。主要的压降还是在滤网上。但是随着夹角α的改变，出水管内压强分布规律发生了明显的变化：夹角α越小，出水管内压强分布越均匀。当夹角α=75°时，出水管上方(即出水管与罐体相交处)，左右两侧即出现漩涡低压区，且压强分布不均匀。当夹角α=45°时，出水管左侧低压区基本消失，虽然右侧低压区还存在，但是出水管内总体压强分布趋于均匀。当夹角α=30°时，出水管上部压强分布十分均匀，这对滤网均匀受压，不至于局部破坏来说十分有利。整个出水管内，压强沿水流方向逐渐减小，压降有明显的过渡过程。

图5 断面压强场Fig.5 Pressure field of the section

4 结 语

(1)根据对过滤器压强场的分析可知，压降主要的部位为滤网。因此保持滤网有关特性不变，而改变出水管与罐体的夹角，对过滤器整体压降影响不大，从焊接罐体与出水管的工艺来说，选择α=90°最为合适。

(2)改变出水管与罐体的夹角α，对进水管、滤网内部、排污管流场的影响比较小，而对出水管的流场有明显的影响，主要表现在：随着夹角α的减小，出水管上部流速、压强分布均趋于均匀；出水管左侧漩涡区域逐渐消失，右侧漩涡区域有所增大。

(3)由于改变出水管角度对过滤器内部流场影响不大，若要对过滤器进行结构优化，改善流场分布，则需要从优化滤网部分着手。

[1] 宗全利,刘 飞,刘焕芳,等.大田滴灌自清洗网式过滤器水头损失试验[J]. 农业工程学报，2012，16:86-92．

[2] 宗全利,刘焕芳,郑铁刚,等. 微灌用网式新型自清洗过滤器的设计与试验研究[J]. 灌溉排水学报,2010,29(1):78-82.

[3] 骆秀萍,刘焕芳,宗全利,等. 自清洗网式过滤器排污流量的计算[J]. 排灌机械工程学报,2012,30(5):588-591,608.

[4] 骆秀萍,刘焕芳,宗全利,等. 微灌自清洗网式过滤器水头损失的试验研究[J]. 石河子大学学报(自然科学版),2011,29(1):98-102.

[5] 刘 飞,刘焕芳,宗全利,等. 新型自清洗网式过滤器结构优化研究[J]. 中国农村水利水电,2010,(10):18-21.

[6] 孙新忠. 离心筛网一体式微灌式过滤器的试验研究[J]. 排灌机械,2006,24(3):20-23.

[7] 李正平. 离心筛网一体式微灌过滤器水力性能试验[J]. 水利与建筑工程学报,2012,10(6):156-159.

[8] 李振成,孙新忠. 离心筛网一体式微灌过滤系统砂粒运移规律的试验研究[J]. 节水灌溉,2013,(2):14-16.

[9] Capra, Scicolone.Assessing dripper clogging and filtering performance using municipal wastewater[J].Irrigation and Drainage, 2005(54):871-879.

[10] Yurdem H, Demir V, Degirmencioglu A. Development of a mathematical model to predict clean water head losses in hydrocyclone filters in drip irrigation systems using dimensional analysis[J]. Biosystems Engineering, 2010,105(4):495-506.

[11] Duran-Ros M, Puig-Bargues J, Arbat G, et al.Performance and backwashing efficiency of disc and screen filters in microirrgation systems[J]. Biosystems Engineering, 2009,103(1):35-42.

[12] 巴 鹏,房元灿,谭效武. 基于CFD技术的管道过滤器内部流场模拟及其结构优化设计[J]. 润滑与密封,2011,36(4):98-101.

[13] 王栋蕾,宗全利,刘建军. 微灌用自清洗网式过滤器自清洗结构流场分析与优化研究[J]. 节水灌溉,2011,(12):5-8,12.

[14] 王新坤,高世凯,夏立平,等. 微灌用网式过滤器数值模拟与结构优化[J]. 排灌机械工程学报,2013,31(8):719-723.

[15] 阿力甫江·阿不里米提,虎胆·吐马尔白,马合木江·艾合买提,等. 直冲洗鱼雷网式过滤器内流场的数值模拟[J].节水灌溉,2014,(10):6-10.

[16] 阿力甫江·阿不里米提,陶洪飞,马英杰,等. 不同出水口位置下全自动鱼雷网式过滤器内部流场的数值模拟[J]. 灌溉排水学报,2015,34(12):47-51.

[17] 李 浩,韩启彪,黄修桥,等. 基于多孔介质模型下微灌网式过滤器CFD湍流模型选择及流场分析[J]. 灌溉排水学报,2016,35(4):14-19.

[18] 王忠义,任翱宇,王纪达,等. 管道过滤器流场数值模拟与实验[J]. 华中科技大学学报(自然科学版),2015,43(1):75-79.

[19] 姚卓飞. 高温陶瓷过滤器的设计与数值模拟研究[D]. 北京：华北电力大学,2015.

[20] 刘 洋. 地下输油管道泄漏污染物迁移过程仿真研究[D]. 黑龙江大庆：东北石油大学,2015.