3DEC中红砂岩节理模型开发及数值模拟

刘清朴，侯 迪，荣 冠

(1. 武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072; 2. 武汉大学 水工岩石力学教育部重点实验室，武汉 430072； 3. 贵州省水利水电勘测设计研究院，贵阳 550002)

0 引 言

天然岩体中存在着大量结构面，如节理、裂隙等。节理力学性质较完整岩石更为复杂，显著影响整个岩体的力学特性。在工程荷载作用下，节理及其力学性质影响着岩体中的应力分布，进而影响岩体工程的稳定性。同时，节理的抗剪强度模型是岩石力学的基础问题和研究的难点。

目前，研究者提出很多节理峰值抗剪强度模型。其中，Patton[1]根据齿状节理直剪试验，提出了反映节理起伏的线性抗剪强度模型。Ladanyi[2]考虑法向应力与节理锯齿起伏的互锁作用关系，提出了节理非线性抗剪强度模型。Barton[3,4]通过引入节理粗糙度系数(JRC)，提出了著名的抗剪强度模型。Plesha[5]假定节理为均匀对称的齿形起伏面，提出了一个在力学上更严格的抗剪强度模型。但上述模型都是基于岩石节理二维形貌参数提出的峰值强度模型，而二维模型难以合理和全面地反映出岩石节理各向异性等力学特性。因此，深入研究节理三维形貌的表征方法，建立岩石节理三维强度模型成为克服节理模型难以准确反映其真实力学特性的关键。Jing[6]研究了节理面的各向异性摩擦角，并参考Plesha模型中剪胀角演化算法，提出了考虑三维各向异性的节理强度模型。夏才初等[7]根据实验结果给出了节理抗剪强度与形貌统计参数Z2的经验关系。Grasselli[8,9]通过大量岩石节理直剪实验，认为在剪切过程中只有面对剪切方向的微单元面才相互接触剪切、磨损，而面向方向的会出现分离，通过研究节理面微元有效剪切倾角与其对应接触面积的统计数学模型，提出了节理三维粗糙度的拟合算法，建立了节理三维抗剪强度模型。唐志成等[10,11]在Grasselli强度模型的基础上，考虑峰值剪胀角与三维形貌特征关系，提出一个可以反映剪胀效应的峰值强度修改模型。

由Cundall于1971年提出来的离散元方法允许不同块体之间产生大的位移甚至脱离接触，并在计算过程中程序能够自动判断块体之间接触状态的变化，适用于解决大位移(诸如滑移、张开或闭合等)的非线性问题，在工程岩体数值分析计算中有着独特的优势。目前离散元程序中节理模型主要有库伦滑移节理模型(Coulomb Slip Model)、连续屈服节理模型(Continuously Yielding Joint Model)、BB模型(Barton-Bandis Joint Model)，但在工程岩体计算分析中，现有模型存在着一些不足。其中，库伦滑移节理模型假定法向变形为线弹性、切向变形为理想弹塑性，所以不能合理的模拟出节理的非线性力学特性。由Cundall和Hart[12]提出的连续屈服节理模型，采用指数方程来表征节理法向变形特征，而由Bandis等[13]提出的法向双曲线方程应用较为广泛，且连续屈服节理模型计算参数需依靠经验确定，无法在工程计算中广泛应用。BB模型剪切方向采用Barton基于节理二维形貌参数提出的剪切强度模型，Hong等[14]指出二维形貌参数会低估节理面的粗糙度，BB模型难以全面反映三维形貌影响下岩石节理剪切力学特性。高艳华等[15]基于试验数据拟合，通过在三维离散元软件3DEC中编写FISH语言动态改变调用的内置节理模型参数，研究了节理剪切力学特性，但通过FISH进行动态修改的方法将大大增加计算时间，特别是在大型岩体工程计算中将影响计算效率。如何基于三维形貌参数把节理非线性变形特征引入到三维离散元软件3DEC中成为了大型工程更加合理模拟分析的关键。

综上所述，本文采用人工劈裂的红砂岩节理进行直剪试验，提出了反映节理三维形貌的红砂岩节理峰值抗剪强度模型。并根据提出的节理峰值抗剪强度修正描述了剪切过程，采用C++语言编写了相应节理模型[16]。在3DEC主程序中模拟了单轴压缩试验和直剪试验，验证了所提模型可以合理反映出红砂岩节理力学特性，为后续研究优势结构面控制下的边坡稳定性及在开挖、支护等工程作用下围岩洞室稳定性分析、安全评价提供基础。

1 节理直剪试验

1.1 试件制备

由于天然岩石节理采集难度较大，因此采用人工劈裂节理进行直剪试验研究。通过采集天然红砂岩制备成尺寸为200 mm×100 mm×100 mm岩石试件(编号为hs-1、hs-2、hs-3、hs-4、hs-5)，并将其劈裂获得新鲜耦合岩石节理(见图1)。试验中使用的红砂岩试件采自湖北鄂州。试件岩石新鲜，颜色为砖红色，主要组成矿物为长石和石英，细砂质结构。利用室内岩石取芯机，对采集的红砂岩钻取直径50 mm 、长度为100 mm 的标准岩样。通过在三轴伺服试验机上进行单轴压缩试验，测量出红砂岩的抗压强度、弹性模量及泊松比。通过岩样用巴西劈裂法测定红砂岩的抗拉强度。并通过对平滑节理面进行反复直剪试验确定试样基本摩擦角。本次试验采用试件的基本力学参数为：单轴抗压强度为65 MPa，抗拉强度2.6 MPa，节理面黏聚力为0 MPa，节理基本摩擦角28°，弹性模量为22.4 GPa，泊松比为0.18。

图1 红砂岩劈裂节理试件Fig.1 Joint specimens of sandstone

1.2 试验方法

试验采用五组红砂岩试件，在耦合状态下使用JAW-1000型岩石节理剪切-渗流耦合试验机(见图2)进行剪切试验。首先按照荷载控制方式施加法向荷载，岩石节理的法向荷载按照σn∶σc(法向荷载：单轴抗压强度) 分别为0.5%、1.0%、1.5%、2.0%、2.5%施加。每次法向荷载按0.1 kN/min加载速率加至预定法向荷载。然后按照位移加载控制方式进行直剪试验，剪切速率为0.5 mm/min。当剪切位移达到10 mm时停止试验，在试验过程中，试验系统通过控制软件可自动采集数据结果。

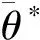
(2)

式中：m为面对剪切方向的单元数；θ*si为第i个面对剪切方向单元的视倾角；Af为面对剪切方向的三角形单元面积总和；At为粗糙节理面实际面积。

图2 剪切渗流耦合试验系统整机图Fig.2 Photograph of coupled shear-flowtest system

图3 KEYENCE_LK-G5000扫描仪及其测量现场Fig.3 The scanner and its measurement field

1.3 试验结果

在法向荷载为0.325、0.65、0.975、1.3、1.625 MPa情况下对红砂岩节理试件进行直剪试验。直剪试验结果及节理三维形貌参数见表1和图4。

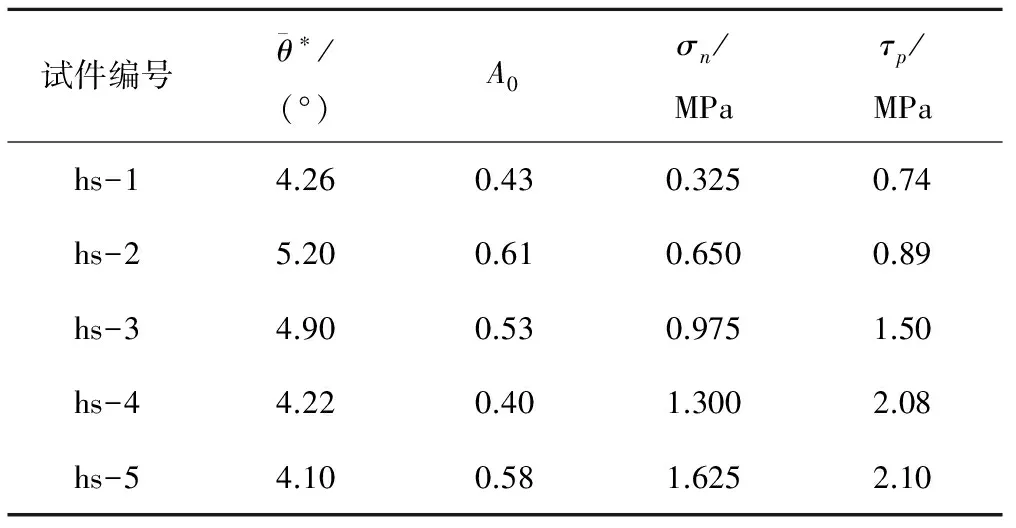
表1 岩石节理形貌参数及强度试验值Tab.1 Morphology parameters and results of shear tests

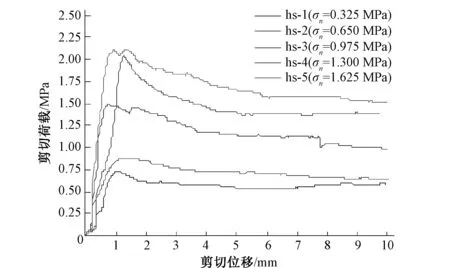
图4 红砂岩试件剪切位移与剪切荷载曲线Fig. 4 Curves of direct shear tests of sandstone

2 节理峰值抗剪强度模型

根据Barton[4]，Grasselli[8,9]，唐志成[10,11]等研究表明，在岩石节理剪切试验中随着法向荷载的增加峰值剪胀角由一个最大值减小到一个恒定值，分析剪胀角与法向荷载的关系可以发现，剪胀角与法向荷载之间符合函数y=1/(1+x)的形式。此外，Grasselli等[9]指出岩石抗拉强度对节理抗剪强度有着重要影响。根据表1和表2分析形貌参数与剪胀角度之间关系可知三维平均倾斜角越大，节理粗糙程度越高，峰值剪胀角度越大；而最大接触面积比越大，说明节理粗糙程度越低，峰值剪胀角越小。峰值剪胀角与法向荷载之间存在如下边界条件：

(3)

式中：i0为节理初始剪胀角；σn为节理法向应力。

根据峰值剪胀角曲线变化规律，考虑上述边界条件，并考虑抗拉强度的影响，而且采用σn/σt作为变量可使得等式左右量纲守恒，提出如下公式：

(4)

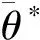
基于Parton公式，即可得岩石节理抗剪强度公式为：

(5)

根据直剪试验数据(见表2)拟合，确定该节理试件经验系数a=0.057 3，b=0.269 9。

为了验证新模型的正确性，采用峰值剪切强度公式(5)计算红砂岩节理试件峰值抗剪强度值，同时采用Barton峰值抗剪强度公式计算，节理试件的JRC值采用Barton[17]的经验公式计算，公式如下：

(6)

式中：L为节理长度；ξ为节理最大凸起程度。

本文每隔1 mm选取沿剪切方向的共9条剖面线计算其ξ值，节理ξ值由组成节理面的9条剖面线的计算值求平均得到。JRC计算结果与节理峰值剪切强度的计算结果列于表2。

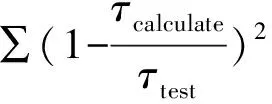
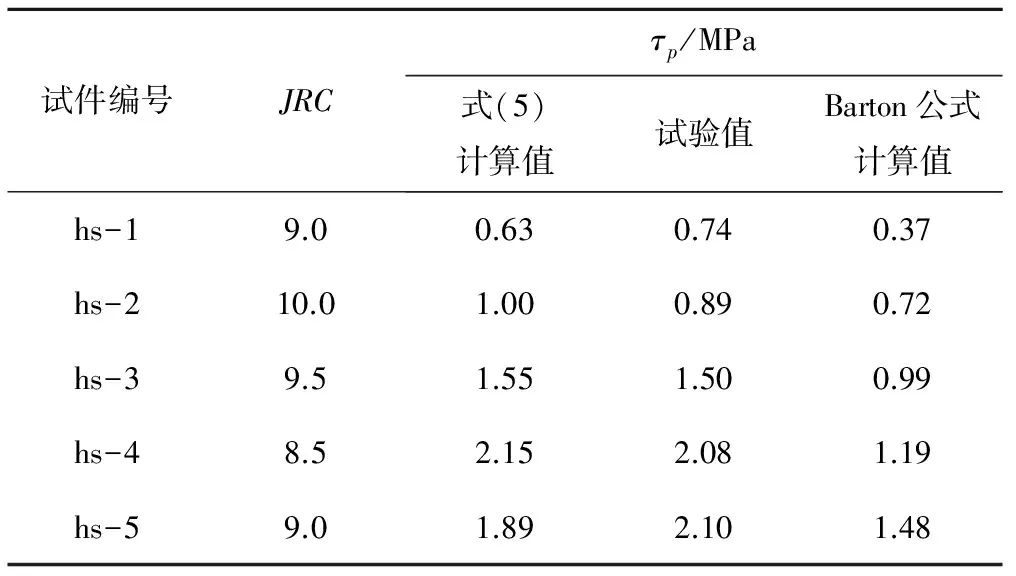
表2 岩石节理强度计算值与试验值对比表Tab.2 Comparison between calculated and observed results

由表2及误差平方和结果可以看到，采用新模型计算岩石节理的峰值剪切强度与试验值更为接近，Barton公式在一定程度上低估了节理的峰值抗剪强度，采用新模型计算节理峰值剪切强度明显优于Barton公式。

3 节理模型二次开发与数值模拟

3.1 节理模型

国内外学者对节理法向变形规律进行过大量研究，主要是根据室内试验得到节理法向应力-节理闭合量曲线。目前应用广泛的为Bandis等[13]基于5种不同岩石(石灰岩、粉砂岩、板岩、砂岩、玄武岩)结构面进行了大量室内试验，指出节理法向应力与法向变形为非线性关系，提出的如下双曲线本构方程：

(7)

式中：ΔVj为节理法向变形；节理初始法向刚度Kni和节理最大闭合量Vm可由Bandis等[13]根据节理粗糙系数JRC、节理壁抗压强度JCS、平均节理缝隙宽度ajn提出的经验公式求出。其中，Bandis提出的Vm经验公式中给出了不同循环加卸载次数下计算参数，为了便于计算，本文仅采用第一次加载曲线。

文献[18]指出对于未风化粗糙节理，影响节理剪切强度的节理因素主要包括节理的粗糙度部分i和基本摩擦角φb两部分。其中，在剪切过程中基本摩擦角可认为不发生变化，其粗糙度呈递减变化。Barton等[18]提出节理表面的粗糙度直接影响剪切强度，通过剪切位移与峰值对应位移的比值修正了节理粗糙系数JRC，得到整个剪切过程的剪切强度。因此，根据上述Barton提出未风化粗糙节理在剪切过程中修正方法，结合1.2节中提出的峰值抗剪强度经验公式(5)，可得出剪切过程中节理切向应力τ为：

τ=σntan (i+φb)

(8)

式中：σn为节理法向应力；φb为基本摩擦角；i=Bip为修正的峰值剪胀角，表示当前状态下节理形貌剪胀效应的大小，ip为峰值剪胀角，B可由表3中A对应计算得出，A是当前的剪切位移与峰值位移的比值，即：A=u/upeak。

表3 系数B的计算对照表[18]Tab.3 values used for calculating the coefficient B[18]

峰值剪切位移upeak由Barton[18]提出的经验计算公式可得：

(9)

在剪切过程中，法向位移增量和切向位移增量的比值定义为剪胀角的正切值。参照Barton[4]提出的关于未风化节理剪胀模型，计算剪切过程中剪胀角dn，其公式为：

(10)

在剪切过程中，法向闭合量不仅与法向应力有关，还受到剪切位移的影响，根据剪胀角的定义对其进行修正，剪切位移引起的Δun的计算公式为：

Δun=Δustandn

(11)

3.2 节理模型的二次开发

三维离散元软件3DEC为用户提供了两种方法来修改节理模型。一种是通过3DEC内部的FISH语言命令对计算过程中调用3DEC原有的模型进行动态修改；该方法编写简单、容易掌握，但其在计算过程中需不断对原有模型的进行动态修改，速度比内置DLL文件模型要慢数倍，直接影响计算效率。另一种是通过3DEC为用户提供的user-defined joint constitutive models 接口，利用C++语言编写相应的节理模型DLL文件(3DEC程序自带模型均是以DLL文件的形式提供给用户)，该方法可以高效、稳定和简洁地将模型嵌入到3DEC程序中。因此，笔者采用第二种方法编写新模型的DLL文件。

3DEC为用户提供了节理模型开发的模板，节理模型开发工作主要是在原有模板基础上，通过Microsoft Visual Studio 2010平台，运用C++语言修改编写新节理模型相应的头文件(.h)和源文件(.cpp)。最终，编译形成相应的动态链接库DLL文件，并进行调试修改。

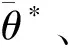
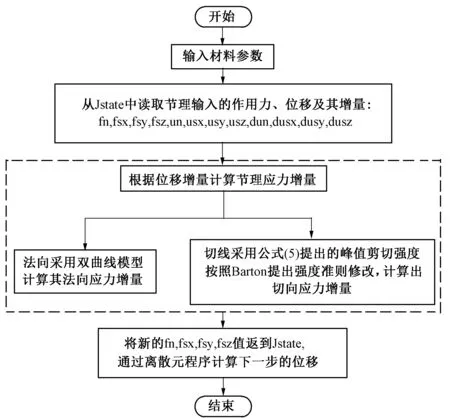
图5 userjbb节理模型开发流程图Fig.5 Development flowchart of userjbb joint model

3.3 节理力学特性模拟

为了验证上述编写的节理模型正确性，本文采用3DEC模拟了单轴压缩试验和直剪试验，与已有成果进行对比分析。为了保持与室内试验相一致，模型尺寸采用200 mm×100 mm×100 mm，该模型为含有一水平节理的岩体。对节理下部岩块底部进行固定，节理上部岩块施加一水平速度，直剪试验中采用与室内试验的相同荷载条件，计算模型如图6所示。

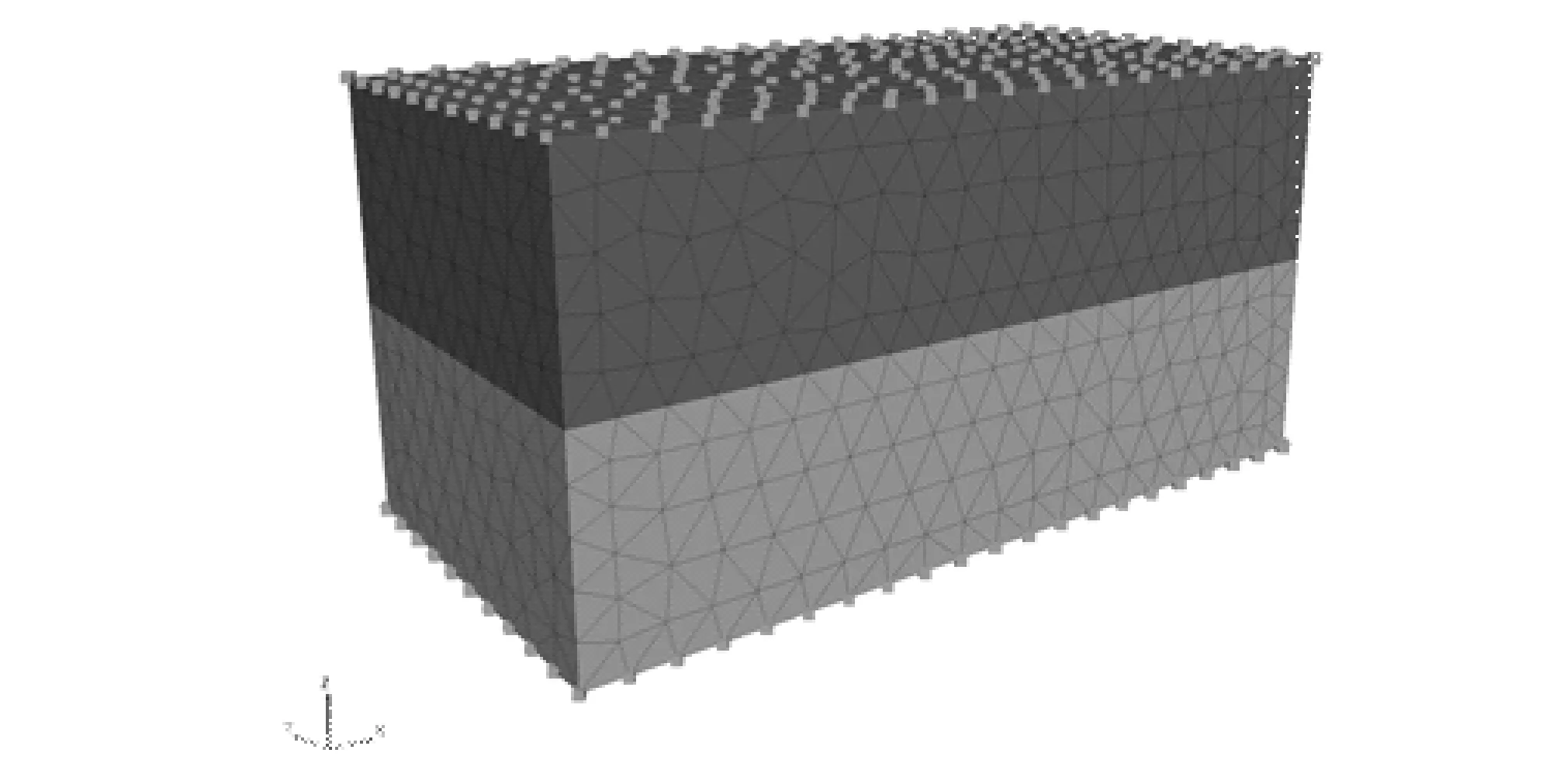
图6 数值模拟计算模型Fig.6 Computational model in numerical simulation

计算模型由岩块和节理两部分组成。BB模型及userjbb模型计算中岩块、节理的力学及几何形貌采用室内试验中hs-3、hs-4两组参数(见表4)。

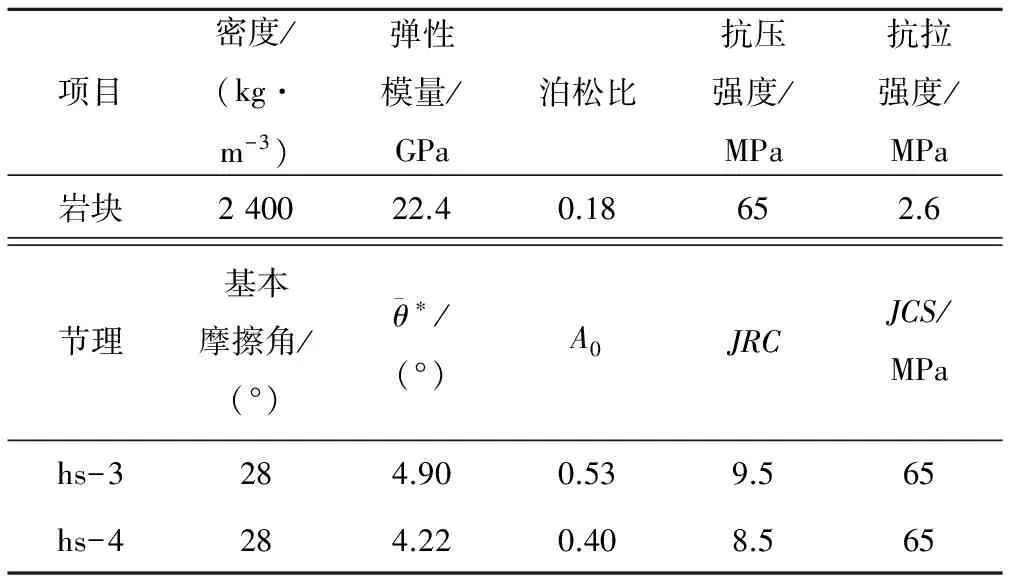
表4 岩体力学及形貌参数Tab.4 Mechanical properties and morphology parameters of rock mass

根据离散元计算原理可知，块体间的整个接触又分成了若干个子接触。因此，在数值模拟计算中，需根据节理面各子接触作用力计算总的应力，并根据节理面子接触的相对位移计算出节理平均位移，取法向为例，其表示式如下：

(13)

式中：n为子接触个数；Fni为第i个子接触法向力；A为整个节理面面积；uni为第i个子接触法向位移。同理，可以计算出平均切向应力和平均切向位移。

3.4 模拟结果分析

通过编写试验相应的3DEC命令代码和平均应力和平均位移计算代码，求出数值模拟过程中整个节理面的平均应力和平均位移。采用userjbb节理模型模拟了单轴压缩试验，对比数值模拟和Bandis提出的双曲线方程理论结果，在三维离散元中可以采用双曲线方程描述节理法向的变形特征，如图7所示。两者计算曲线十分接近，变形规律如下：随着法向应力的增加，法向闭合量增加速率逐渐增大，法向闭合量不断增加，最终趋近于最大闭合量。在法向应力较小时，其法向闭合量与法向应力近似为线性。但是当应力较大时，节理法向非线性变形特征尤为突出。

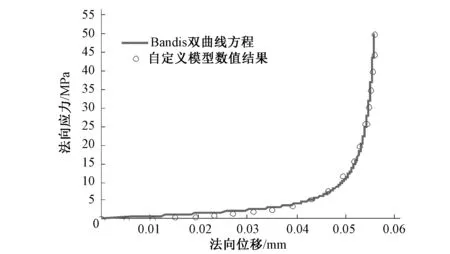
图7 节理法向应力-法向位移数值试验与理论结果Fig.7 Numerical and theoretical results of joint normal stress vs normal displacement

采用三维离散元程序中userjbb节理模型及二维离散元程序中BB模型模拟了红砂岩节理的直剪试验，并与室内直剪试验结果进行了对比，如图8所示。图8表明数值模拟计算结果、试验结果均表现了节理剪切应力-剪切变形的总体规律为非线性：在常法向应力下节理剪切应力随着剪切位移的增加而增加至峰值抗剪强度，之后随着剪切位移的增加而衰减，衰减到残余剪切强度后保持不变。其中，采用userjbb节理模型的数值结果和试验结果吻合较好，而BB模型数值结果明显低于userjbb节理模型的数值结果和试验结果。究其原因为：岩体节理表面为凸凹不平的三维粗糙面，其表面上随机分布了一些微凸体。随着剪切位移的增加，节理面上的微凸体发生咬合、爬坡等现象。当作用在微凸体上的法向应力大于其所能承受的最大应力时，则会导致节理微凸体的磨损甚至破碎。充分考虑节理形貌特征，将其引入到剪切强度计算中成为合理反映剪切强度的关键。而在BB模型中仅考虑了节理的二维形貌，计算结果偏于保守，不能反映出节理三维形貌对剪切强度的影响。

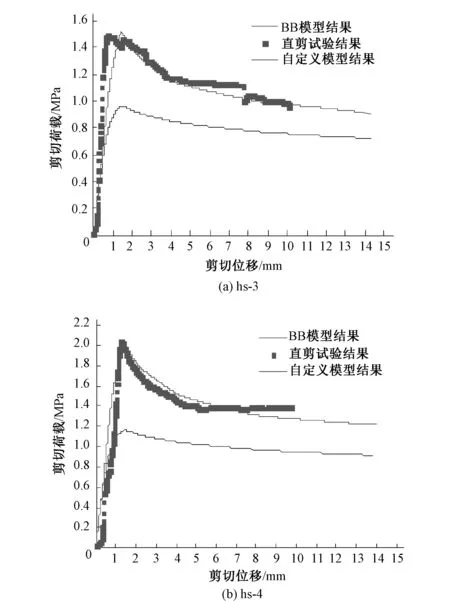
图8 红砂岩节理数值模拟与直剪试验结果Fig.8 Numerical and test results of sandstone joint

4 结 语

(2)分别采用提出的峰值抗剪强度模型和Barton模型计算了相应的峰值强度值，并与室内试验结果对比分析，分析表明：新模型能更好地描述节理峰值剪切强度，Barton模型在一定程度上低估了节理的峰值抗剪强度。

(3)基于3DEC提供的接口，采用C++语言编写相应的DLL文件，实现了将建立节理非线性本构模型内嵌于3DEC中。通过数值模拟分析验证，该方法是一种行之有效的方法。

(4)通过数值模拟与试验结果对比，可以得出：采用新模型的数值结果与理论、试验结果吻合较好，可以合理反映出红砂岩节理力学特性。

□

[1] Patton F D. Multiple modes of shear failure in rock[C]∥1st ISRM Congress. International Society for Rock Mechanics, 1966.

[2] Ladanyi B, Archambault G. Simulation of shear behavior of a jointed rock mass[C]∥The 11th US Symposium on Rock Mechanics (USRMS). American Rock Mechanics Association, 1969.

[3] Barton N. Review of a new shear-strength criterion for rock joints[J]. Engineering Geology, 1973,7(4):287-332.

[4] Barton N, Choubey V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics, 1977,10(1-2):1-54.

[5] Plesha M E. Constitutive models for rock discontinuities with dilatancy and surface degradation[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1987,11(4):345-362.

[6] Jing L. Numerical modelling of jointed rock masses by distinct element method for two-and three-dimensional problems[D]. Luleå: Luleå Tekniska Universitet,1990.

[7] 夏才初, 孙宗颀. 工程岩体节理力学[M]. 上海：同济大学,2002.

[8] Grasselli G, Wirth J, Egger P. Quantitative three-dimensional description of a rough surface and parameter evolution with shearing[J]. International Journal of Rock Mechanics and Mining Sciences, 2002,39(6):789-800.

[9] Grasselli G, Egger P. Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters[J]. International Journal of Rock Mechanics and Mining Sciences, 2003,40(1):25-40.

[10] 唐志成, 夏才初, 宋英龙, 等. Grasselli节理峰值抗剪强度公式再探[J]. 岩石力学与工程学报, 2012,31(2):356-364.

[11] 唐志成, 夏才初, 宋英龙. 粗糙节理的峰值抗剪强度准则[J]. 岩土工程学报, 2013,35(3):571-577.

[12] Cundall P A, Hart R D. Analysis of block test no. 1 inelastic rock mass behavior: phase 2-a characterization of joint behavior(final report)[R]. Itasca Consulting Group, 1984.

[13] Bandis S C, Lumsden A C, Barton N R. Fundamentals of rock joint deformation[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon, 1983,20(6):249-268.

[14] Hong E S, Lee J S, Lee I M. Underestimation of roughness in rough rock joints[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008,32(11):1 385-1 403.

[15] 高艳华, 吴顺川, 王 贺, 等. 基于持续屈服节理模型的节理直剪数值试验[J]. 中南大学学报 (自然科学版), 2016,(4):23.

[16] Itasca Consulting Group Inc. 3DEC (3 dimensional distinct element code) Constitutive Models[R]. Itasca Consulting Group Inc.，2013.

[17] Barton N, de Quadros E F. Joint aperture and roughness in the prediction of flow and groutability of rock masses[J]. International Journal of Rock Mechanics and Mining Sciences, 1997,34(3-4):252.e1-252.e14.

[18] Barton N. Modelling rock joint behavior from in situ block tests: implications for nuclear waste repository design[R]. USA: Terra Tek, Inc., Salt Lake City, UT, 1982.