多相材料有效性能预测的高精度方法1)
朱合华陈 庆
∗(同济大学土木工程防灾国家重点实验室、岩土及地下工程教育部重点实验室,上海200092)
†(同济大学先进土木工程材料教育部重点实验室,上海200092)
多相材料有效性能预测的高精度方法1)
朱合华∗,2)陈 庆†,3)
∗(同济大学土木工程防灾国家重点实验室、岩土及地下工程教育部重点实验室,上海200092)
†(同济大学先进土木工程材料教育部重点实验室,上海200092)
有效介质方法是常用的细观力学方法之一.其可用于计算多相材料的有效性能,并建立材料微细观结构和宏观性能的定量关系;有助于指导新材料设计,减少试验工作量等.然而,当夹杂含量升高时,传统有效介质方法的计算精度下降.本文以两相材料为研究对象,提出一种新的参考介质,即:为更合理考虑不同夹杂颗粒间的相互作用,假定参考介质的应变是基体相平均应变和某一修正张量的双点积.在此基础上,推导了新参考介质下两相材料的有效模量表达式,并给出该修正张量的近似计算方法;通过反复更新参考介质,采用多层次均匀化思路,将本文方法进一步用于多相材料性能的预测.为验证方法的有效性,将预测结果与已有模型结果和试验数据进行对比.结果表明本文方法较已有方法更为合理、有效.当夹杂含量升高时,本文方法较传统有效介质方法的计算精度有所提升.
高精度方法,高夹杂含量,多夹杂,多层次均匀化,细观力学
引言
细观力学常采用有效介质方法预测复合材料的有效模量,如Eshelby法、Mori-Tanaka(M-T)法、自洽法和微分法等[1-2].文献[3-9]将有效介质方法应用于岩石和混凝土有效模量的预测,文献[10-15]则将该方法应用于饱和与非饱和混凝土电化学沉积修复的细观力学模型.
然而,有效介质方法在计算高夹杂含量复合材料有效模量时较难获得满意的结果.比如,Eshelby法要求夹杂极其稀疏;随着夹杂含量的增大,当夹杂刚度低于(或高于)基体刚度时,M-T方法会高估(或低估)复合材料的有效模量,而自洽法会低估(或高估)复合材料的有效性能,并且自洽法不具备显式表达,需要进行迭代求解;应用微分法预测有效模量时,需要求解非线性微分方程组,给工程应用带来不便[1-2].
Ju等[16-19]近期通过假设夹杂在基体中的分布形式,基于Eshelby理论,直接计算了不同夹杂颗粒间的相互作用,得到高夹杂含量(达50%)复合材料性能高精度预测方法[16-19].可是,由于很难直接计算多相材料中不同颗粒之间的相互影响,该方法目前还仅限于两相材料的性能预测,无法用于计算多相材料的有效性能.
为了解决传统有效介质法因夹杂含量增大导致计算精度下降的问题,本文提出一种多相材料性能的高精度预测方法.具体而言:首先以两相材料为对象,定义参考介质的刚度和基体相相同,参考介质的应变为基体相平均应变和待定修正四阶张量的双点积;然后,结合Ju等近期提出的两相材料性能高精度预测方法,求解该四阶张量的解析表达式,获得高精度预测方法的参考介质性能;最后,通过不断更新参考介质应变修正张量,采用多层次均匀化的方法,获得多相材料有效模量的高精度预测方法.
1 两相材料的有效模量
1.1 有效模量的定义
由于复合材料的微细观结构复杂,常采用代表性体积单元(representative volume element,RVE)的方法进行表征.所谓代表性体积单元是基于细观尺度定义的,一般其尺寸远大于夹杂相的尺寸,而远小于宏观尺寸.以两相材料为例,其有效刚度C∗定义如下[1]
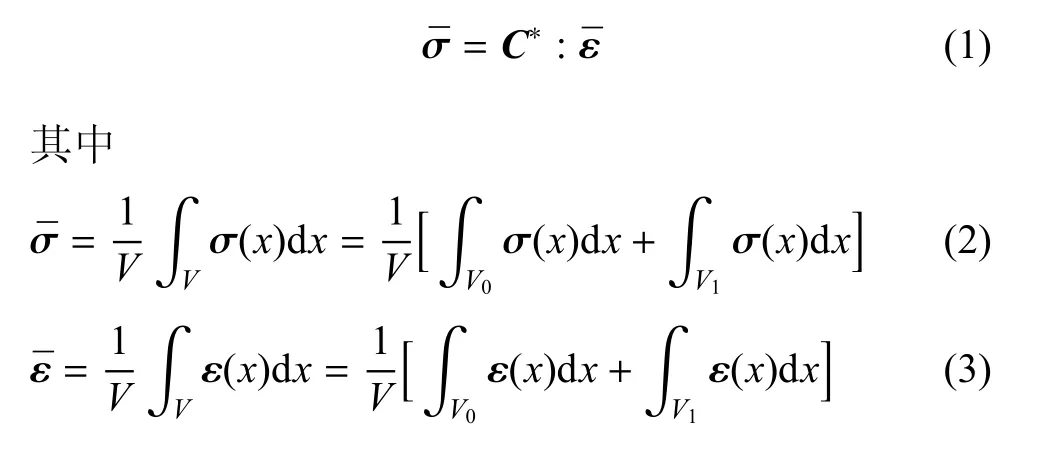
式中,V是代表性体积单元的体积,V0是基体的体积;V1是夹杂相的体积,为平均应变,为平均应力.
1.2 有效介质法简介
Eshelby求解了载荷作用下无限大弹性体中含单个椭球型夹杂的应力和应变问题[20-22].而工程材料常含有不同的夹杂相,并且同一夹杂相也有不同颗粒.在载荷作用下,不同夹杂颗粒将相互影响,使得工程材料内部的应变分布很难精确求解.为简化这一求解过程,有效介质法试图基于Eshelby的成果并通过引入参考介质的方式来近似处理夹杂颗粒之间的相互影响.具体而言如下[1].
(1)Eshelby法假设参考介质的刚度C为基体的刚度C0,参考介质的应变ε为复合材料的平均应变,即假设

(2)M-T法假设参考介质的刚度C为基体的刚度C0,参考介质的应变ε为基体的平均应变即
假设
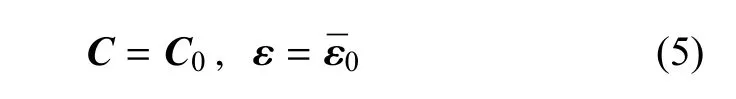
(3)自洽法假定参考介质的刚度C为复合材料的有效刚度C∗,参考介质的应变ε为复合材料的应变即
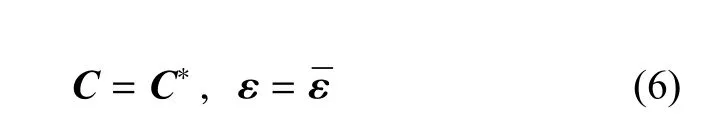
当基体相和夹杂相都是各向同性、且夹杂相的形状为球形时,由M-T法预测的两相材料的体积模量和剪切模量如下
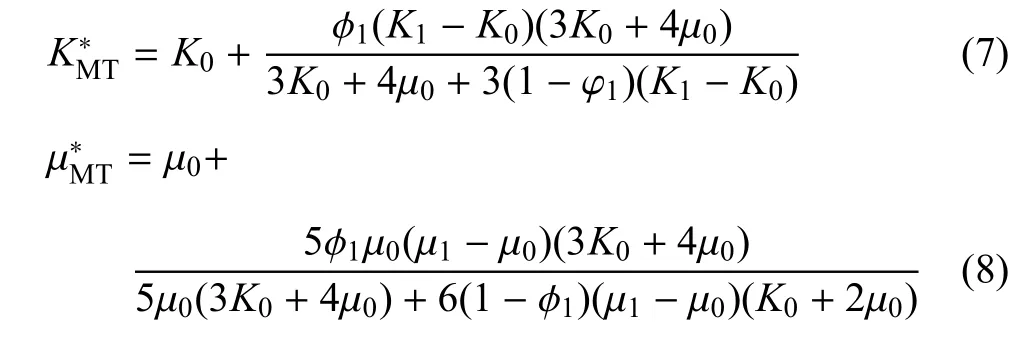
2 两相材料性能预测的高精度方法
2.1 新参考介质定义
借鉴传统有效介质方法的假设,为了获得有效模量的显式表达,一般假设参考介质的刚度为基体刚度.为此:
(1)借鉴Eshelby法和M-T法的假定,本文新参考介质的刚度假定为基体的刚度C0

式中,C是参考介质的刚度张量.
(2)为了更合理考虑不同夹杂间的影响程度,参考介质的应变取待定修正张量和基体相材料平均应变的双点积

式中,U和ε分别是修正四阶张量和参考介质的应变.如果U=I(I是四阶单位张量),那么本文方法就和M-T方法相同.因此,不妨认为本文方法是一种改进的M-T方法.
2.2 新参考介质下两相材料有效模量求解
根据Eshelby的成果,在新参考介质作用下,有下式成立[1]

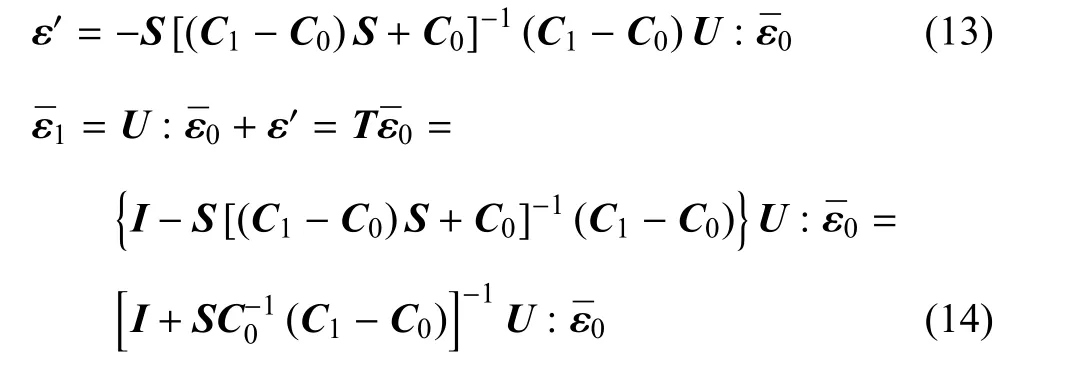
式中,T是关联基体平均应变和夹杂平均应变的转换张量.
假设基体相和夹杂相符合胡克定律,并根据代表性体积单元平均应变和平均应力的定义有
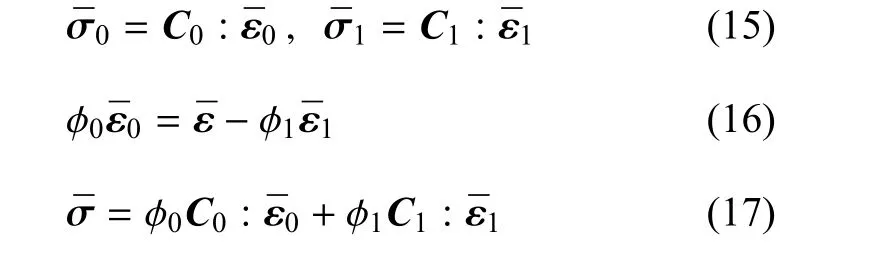
式中φ0和φ1是代表性体积单元中基体和夹杂的体积含量;是代表性体积单元中基体、夹杂和复合材料的平均应变(应力).
将式(14)代入式(16)可以得到
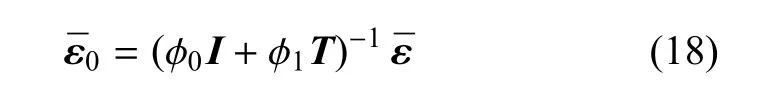
联合式(14),式(17)和式(18)可以得到
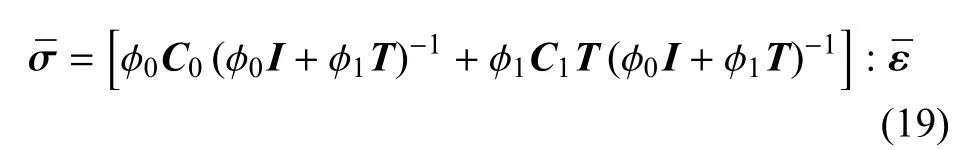
所以,本文参考介质下两相材料的有效模量C∗可由式(20)表示

2.3 待定的四阶张量的近似求解
通过直接考虑夹杂颗粒间相互作用,笔者近期提出了一种高夹杂含量下(达到50%)两相材料性能预测的高精度细观力学方法[16-19].该方法的应变集中张量表达式如下

式中K0,G0,ν0是基体的体积模量,剪切模量和泊松比;K1,G1是夹杂的体积模量和剪切模量.
另外,根据文献[1]可得本文方法的应变集中张量为

如果基体和夹杂都是各向同性,且夹杂的形状为球形,假设式(21)和式(27)相等,经过推导,可以得到待定的四阶张量为

式(28)等号右边各张量的分量如下
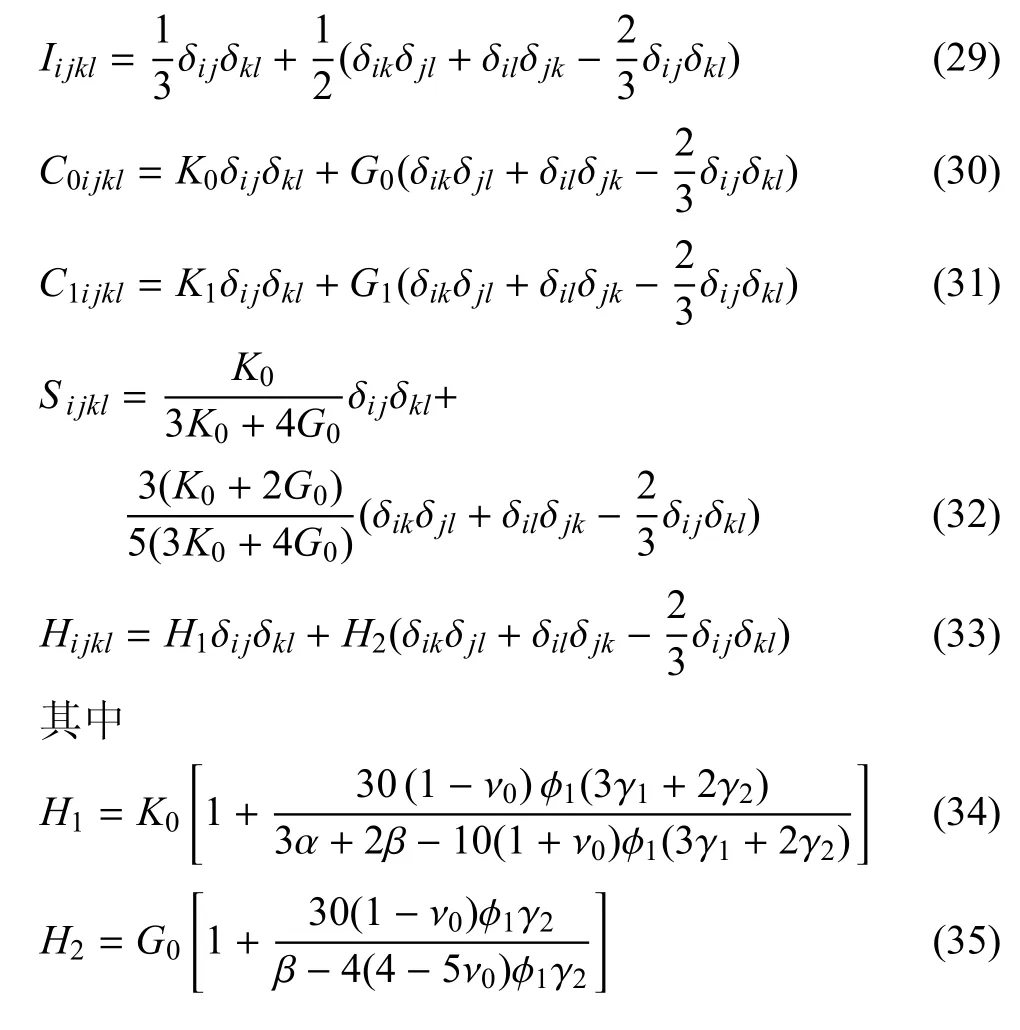
式中δij克罗内克符号.那么,张量U的分量可表达如下

3 多相材料性能预测的高精度方法
3.1 多层次均匀化的思路
第2节关于修正张量U的求解,是借鉴了笔者近期两相材料有效性能预测的结果,因此,该张量U尚无法直接用于多相复合材料的性能预测.为此,本节将进一步借鉴有效介质法的思路,通过反复更新参考介质的性能,采用多层次均匀化思路将第二节提出方法用于多相材料性能预测[10-15,25-27].
假设有n+1相材料,其含有第1,2,··,n种夹杂.为获取其有效性能,可采用多层次均匀化思路如下:先通过第1层均匀化获取基体和第1种夹杂组成的等效材料,然后以此为新基体,通过第2层次均匀化,获得新基体和第2种夹杂组成的等效材料,接着,又以此作为新的基体,依此类推,通过n层均匀化即可得到n+1相复合材料材料的有效性能[10-15,25-27].
3.2 多相材料性能预测
以n+1相材料为例,即除基体相外,还有第1,2,··,n相夹杂.其中基体相的体积为V0,刚度为C0;第1,2,··,n相夹杂的体积分别为V1,V2,··,Vn;刚度分别为C1,C2,··,Cn.
首先,采用本文改进的有效介质方法进行第一层次均匀化处理,获得基体和第一种夹杂组成的等效材料的有效性能.具体如下

接着,采用本文方法进行第二层次均匀化处理,获取由基体和第一、二两种夹杂组成的三相材料的有效性能.具体如下所示
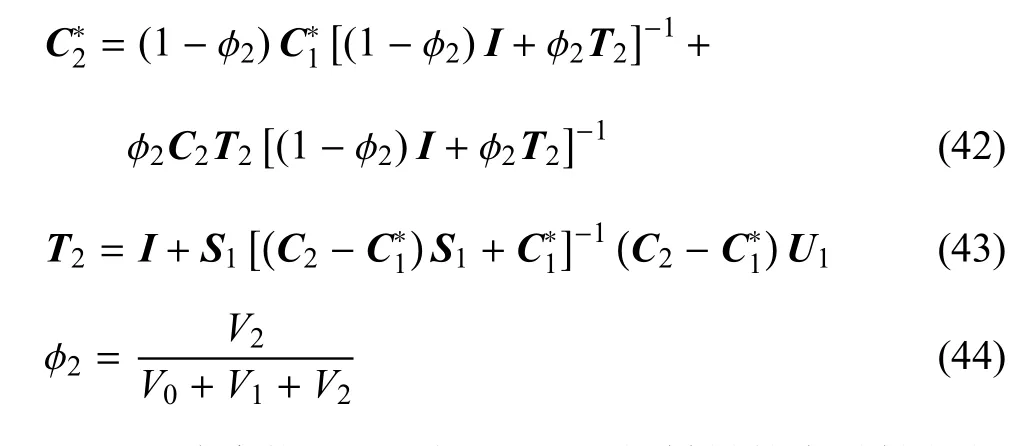
依此类推,可以得到n+1相材料的有效性能如下
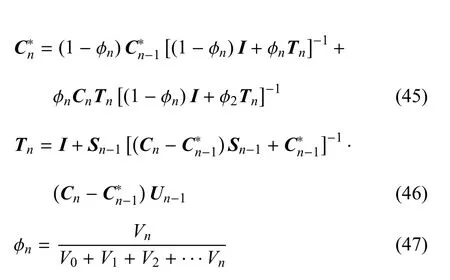
式中,S0,S1和Sn-1是分别对应于基体相(更新前的基体),第一次均匀化后的等效材料(更新一次后的基体),第n-1次均匀化后的等效材料(更新n-1次后的基体)含球形夹杂时的Eshelby张量;U0,U1和分别是基体和第一相夹杂,第一次均匀化后等效材料(更新一次后的基体)和第二相夹杂,以及第n-1次均匀化后等效材料(更新n-1次后的基体)和第n相夹杂组成的两相材料的参考介质应变修正张量.
4 对比验证
为了验证本章提出的模型,本文采用文献[28-29]的试验数据进行对比分析.其中,文献 [28]的材料参数是E0=3.0GPa,ν0=0.4,E1=76GPa,ν1=0.23.文献[29]的材料参数是E0=0.75×106bars和ν0=0.23.材料的体积模量K和剪切模量G按如下关系式换算
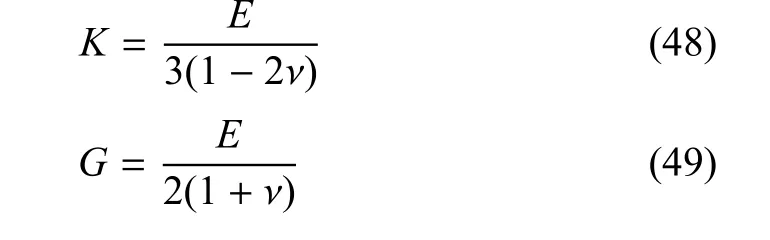
将以上材料参数代入式(7)和式(8)可获得M-T方法的计算结果;对于本文方法,首先将以上材料参数带入式(37)和式(38)可以获得修正张量U;然后根据式(14)可求得张量T,最后根据式(20)计算本文结果.图1表示传统M-T法与本文法预测的杨氏模量和文献[28]的试验数据对比情况.从图1中可以看出,本文方法预测的有效杨氏模量和试验数据吻合的很好,在夹杂含量较低时,传统M-T方法预测结果也可较好地反应该试验的结果.随着颗粒含量的提升,本文方法的精度更高.
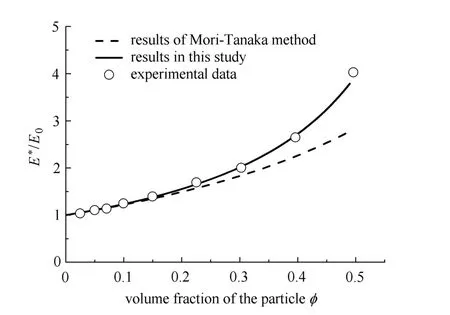
图1 杨氏模量对比图Fig.1 The comparisons among the Young’s modulus obtained by experiment and di ff erent micromechanical methods
图2表示传统M-T法与本文方法预测的剪切模量和文献[28]的试验数据对比情况.从图2可知,在低夹杂含量下,传统M-T方法和本文方法的结果相近,且都与试验结果吻合较好;当高夹杂含量增加时,本文方法预测的有效剪切模量依然与试验数据吻合的很好,而传统M-T方法预测结果偏离试验结果较多.
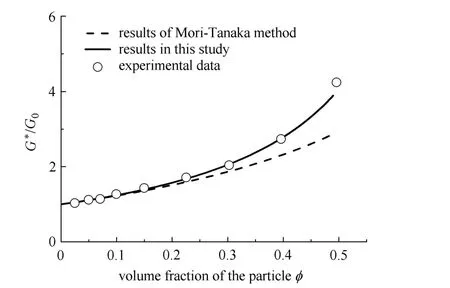
图2 剪切模量对比图Fig.2 The comparisons among the shear modulus obtained by experiment and di ff erent micromechanical methods
图3表示M-T法与本文方法预测的体积模量及文献[29]的试验数据对比情况.同样,无论是低孔隙率还是高孔隙率(50%),本文方法都可以很好地预测试验结果;而传统的M-T方法预测的有效体积模量随着孔隙率的增加精度呈下降趋势.
从上面的3个例子可以看出,对于两相材料有效模量的预测(含杨氏模量、剪切模量和体积模量),当夹杂含量增加时,本文方法的计算精度要高于传统的M-T方法.
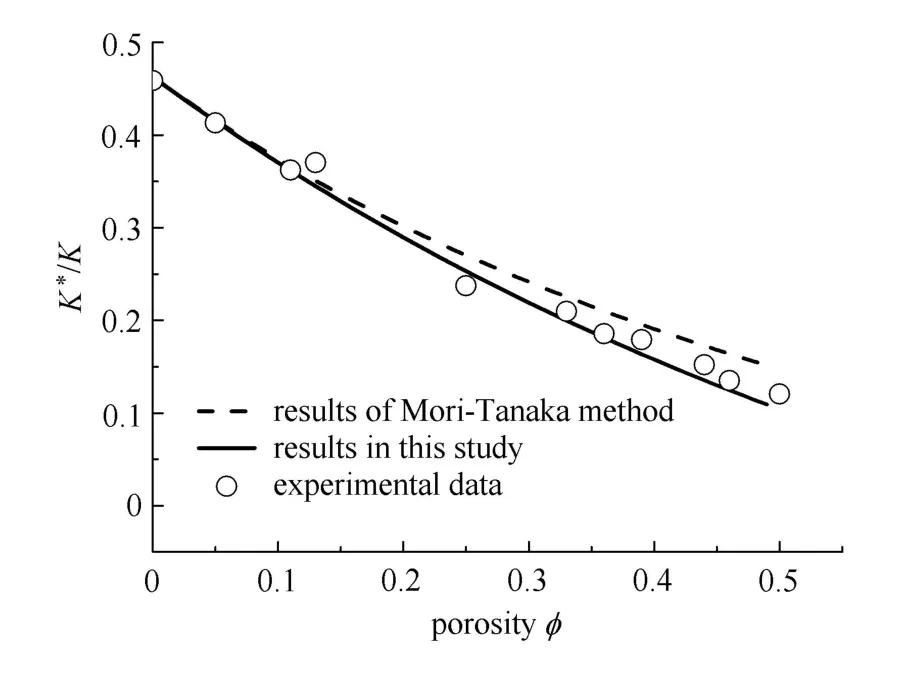
图3 体积模量对比图Fig.3 The comparisons among the bulk modulus obtained by experiment and di ff erent micromechanical methods
为进一步验证本文方法在多相材料性能预测中的可行性,取文献[30]的试验结果作为对比对数.该试验材料是由基体相孔隙相和增强相组成,其中基体相的性能为E0=2.2GPa,ν0=0.3;孔隙相的模量取为0;增强相的性能为E1=75GPa,ν1=0.25.随着孔隙含量和增强相的变化,三相材料的整体性能也将随之变化.表1是不同细观力学模型预测结果和试验结果的对比情况.从表1中可以看出,本文方法与M-T方法预测结果相近.但是,本文方法预测结果(平均误差8.6%)比M-T方法(平均误差11.8%)更接近试验结果.
5 结论
当夹杂含量较高时,传统有效介质方法的计算精度会下降.本文通过改变传统有效介质法中参考介质的应变来提升其计算精度,即:假设参考介质的应变是基体相平均应变和某一修正张量的双点积;并基于笔者近期的成果给出了两相材料该修正张量的近似计算方法;进一步,通过不断更新修正张量,采用多层次均匀化思路,预测了多相材料的性能.经对比验证,本文方法计算结果较传统有效介质方法(以Mori-Tanaka为例)更合理、有效.

表1 不同细观力学模型预测结果和试验结果对比Table 1 The comparisons among the results obtained by experiment and dif f erent micromechanical methods
致谢感谢美国UCLA的朱建文教授在论文写作过程中给予的指导.
1 Qu JM,Cherkaoui M.Fundamentals of Micromechanics of Solids. Hoboken,New Jersey:John Wiley&Sons,Inc.2006
2 Mura T.Micromechanics of Defects in Solids.The Netherlands:Martinus Nijhof fPublishers,1987
3 Sheng P.Ef f ective-medium theory of sedimentary rocks.Physical Review B,1990,41:4507-4512
4 Sheng P,Callegari A.Dif f erential ef f ective medium theory of sedimentary rocks.Applied Physics Letters,1984,44:738-740
5 Nguyen N,Giraud A,Grgic D.A composite sphere assemblage model for porous oolitic rocks.International Journal of Rock Mechanics and Mining Sciences,2011,48:909-921
6 Li G,Zhao Y,Pang SS.Four-phase sphere modeling of ef f ective bulk modulus of concrete.Cement and Concrete Research,1999, 29:839-845
7 Wang H,Li Q.Prediction of elastic modulus and Poisson’s ratio for unsaturatedconcrete.InternationalJournalofSolidsandStructures, 2007,44:1370-1379
8 Yaman I,Aktan H,Hearn N.Active and non-active porosity in concrete part II:evaluation of existing models.Materials and Structures,2002,35:110-116
9 王海龙,李庆斌.饱和混凝土的弹性模量预测.清华大学学报(自然科学版),2005,45(6):761-763(Wang Hailong,Li Qingbin. Saturated concrete elastic modulus prediction.Journal of Tsinghua University(Science and Technology),2005,45(6):761-763(in Chinese))
10 Zhu HH,Chen Q,Yan ZG,et al.Micromechanical model for satu-rated concrete repaired by electrochemical deposition method.Materials and Structures,2014,47:1067-1082
11 Yan ZG,Chen Q,Zhu HH,et al.A multiphase micromechanical model for unsaturated concrete repaired by electrochemical deposition method.International Journal of Solids and Structures,2013, 50(24):3875-3885
12 陈庆.多相材料随机细观力学模型及其在电化学沉积修复混凝土中的应用.[博士论文].上海:同济大学,2014(Chen Qing.The stochastic micromechanical models of the multiphase materials and their applications for the concrete repaired by electrochemical deposition method.[PhD Thesis].Shanghai:Tongji University,2014(in Chinese))
13 陈庆,朱合华,闫治国等.基于Mori-Tanaka法的电化学沉积修复饱和混凝土细观描述.建筑结构学报,2015,36(1):98-103 (Chen Qing,Zhu Hehua,Yan Zhiguo,et al.Micro-scale description of the saturated concrete repaired by electrochemical deposition method based on Mori-Tanaka method.Journal of Building Structures,2015,36(1):98-103(in Chinese))
14 陈庆,朱合华,闫治国等.基于自洽理论的电化学沉积修复饱和混凝土细观描述.力学学报,2015,47(2):367-371(Chen Qing,Zhu Hehua,Yan Zhiguo,et al.Micro-scale description of the saturated concrete repaired by electrochemical deposition method based on self-consistent method.Chinese Journal of Theoretical and Applied Mechanics,2015,47(2):367-371(in Chinese))
15 Chen Q,Jiang ZW,Yang ZH,et al.Dif f erential-scheme based micromechanical framework for saturated concrete repaired by the electrochemical deposition method.Materials and Structures,2016, 49(12):5183-5193
16 Ju JW,Chen T.Ef f ective elastic moduli of two-phase composites containing randomly dispersed spherical inhomogeneities.Acta Mechanica,1994,103:123-144
17 Ju JW,Chen T.Micromechanics and ef f ective moduli of elastic composites containing randomly dispersed ellipsoidal inhomogeneities.Acta Mechanica,1994,103:103-121
18 Chen Q,Zhu HH,Ju JW,et al. A stochastic micromechanical model for multiphase composite containing spherical inhomogeneities.Acta Mechanica,2015,226(6):1861-1880
19 Zhu HH,Chen Q,Ju JW,et al.Maximum entropy based stochastic micromechanical model for two-phase composite considering the inter-particle interaction ef f ect.Acta Mechanica,2015,226(9):3069-3084
20 Eshelby JD.The determination of the elastic fiel of an ellipsoidal inclusion,and related problems.Proceedings of the Royal Society of London.Series A.Mathematical and Physical Sciences,1957,241:376-396
21 Eshelby JD.The elastic fiel outside an ellipsoidal inclusion.Proceedings of the Royal Society of London.Series A,Mathematical and Physical Sciences,1959,252:561-569
22 Eshelby JD.Elastic inclusions and inhomogeneities.Progress in Solid Mechanics,1961,2:89-140
23 Mori T,Tanaka K.Average stress in matrix and average elastic energy of materials with misfittininclusions.Acta metallurgica, 1973,21:571-574
24 Benveniste Y.A new approach to the application of Mori-Tanaka’s theory in composite materials.Mechanics of materials,1987,6:147-157
25 Chen Q,Zhu HH,Yan ZG,et al.A multiphase micromechanical model for hybrid fibe reinforced concrete considering the aggregate and ITZ ef f ects.Construction and Building Materials,2016, 114:839-850
26 Nezhad MM,Zhu HH,Ju JW,et al.A simplifie multiscale damage model for the transversely isotropic shale rocks under tensile loading.International Journal of Damage Mechanics,2016,25:705-726
27 ChenQ,NezhadMM,FisherQ,etal.Multi-scaleapproachformodeling the transversely isotropic elastic properties of shale considering multi-inclusions and interfacial transition zone.International Journal of Rock Mechanics and Mining Sciences,2016,84:95-104
28 Smith JC.Experimental values for the elastic constants of a particulate-filleglassy polymer.Journal of Research of the National Bureau of Standards,1976,80A:45-49
29 Walsh JB,Brace WE,England AW.Ef f ect of porosity on compressibility of glass.Journal of the American Ceramic Society,1965,48:605-608
30 Cohen L,Ishai O.The elastic properties of three-phase composites.Journal of Composite Materials,1967,1:390-403
AN APPROACH FOR PREDICTING THE EFFECTIVE PROPERTIES OF MULTIPHASE COMPOSITE WITH HIGH ACCURACY1)
Zhu Hehua∗,2)Chen Qing†,3)
∗(China State Key Laboratory for Disaster Reduction in Civil Engineering,Key Laboratory of Geotechnical and Underground Engineering of the Ministry of Education,Tongji University,Shanghai200092,China)
†(Key Laboratory of Advanced Civil Engineering Materials of Ministry of Education,Tongji University,Shanghai200092,China)
The ef f ective medium approach is one of the common micromechanical methods,which can be utilized to predict the material’s ef f ective properties and set up the quantitative relationship between the material’s microstructures and macroscopic properties.It is helpful and meaningful for the new material design and reducing the(experimental) workload to use these micromechanical estimations of the material’s properties.However,the calculation accuracy will decline when the ef f ective medium method is adopted to estimate the ef f ective properties of the composite with high volume fraction of inclusions.Therefore,in this paper the two-phase composite is taken as the example firstl and the strain of the reference medium is assumed to be the product of the average strain of the matrix and a modifying tensor. Thentheexpressionsoftheef f ectivemodulusarederivedwiththeproposedreferencemedium.What’smore,thesolutions for modifyingtensorarereached by using theachievementwe obtained recently.Further,through optimizingthereferencemedium repeatedly,with the help of multi-level homogenization scheme,the proposed modifie method is extended to predict the properties of the multiphase composite with many types of inclusions.To verify our proposed framework, the predictions are compared with the experimental data and the results of existing models.The comparisons show that the estimations of the presented method are more reasonable and acceptable.When the volume fraction of inclusions is higher,the calculation accuracy of the presented method in this paper is better than those of the existing ef f ective medium methods.
high accuracy approach,high volume fraction of inclusion,multi-inclusions,multi-level homogenization, micromechanics
O343.7
A doi:10.6052/0459-1879-16-347
2016-11-25收稿,2016-11-28录用,2016-12-02网络版发表.
1)国家自然科学基金(51508404,U1534207)和高性能土木工程材料国家重点实验室(2015CEM008)资助项目.
2)朱合华,教授,主要研究方向:隧道及地下结构计算方法.E-mail:zhuhehua@tongji.edu.cn
3)陈庆,助理研究员,主要研究方向:混凝土修复,细观力学,地下结构.E-mail:chenqing19831014@163.com
朱合华,陈庆.多相材料有效性能预测的高精度方法.力学学报,2017,49(1):41-47
Zhu Hehua,Chen Qing.An approach for predicting the e ff ective properties of multiphase composite with high accuracy.Chinese Journal of Theoretical and Applied Mechanics,2017,49(1):41-47

