基于PIV的泥泵叶轮内颗粒相对速度场的研究

徐立群，倪福生，刘明星，顾 磊

（1.河海大学疏浚技术教育部工程研究中心，江苏常州 213022；2.河海大学，江苏常州 213022）

1 前言

疏浚施工过程中，泥泵被用来抽吸和输送浆体，为管道输送提供动力，是挖泥船的核心设备，其正常运转是疏浚任务顺利完成的保障。而且，疏浚船舶的大部分功率都消耗在泥泵上，其性能决定了疏浚船舶的动力配置和施工效益［1~4］。泥泵的性能受诸多因素影响，其中叶轮内泥砂颗粒的运动甚为关键，是研究泥泵性能的重要方面。

PIV测量技术即粒子图像测速技术，是一种瞬态、全流场、无干扰的测量技术［5］。该技术可直接测得泵内流场，被广泛用于研究泵叶轮的内部流动［6~10］，取得了长足的进展。但可以发现，针对疏浚行业泥泵内部流动的研究较为少见，已有研究中颗粒直径均相对较小。为此，本文扩大颗粒粒径范围，在河海大学疏浚技术教育部工程中心的疏浚泥泵透明试验平台上，采用PIV系统测量颗粒在泥泵叶轮内的相对速度场，以期为研究叶轮内颗粒的运动规律提供参考。

2 试验介绍

2.1 模型泵

本试验采用的模型泵是依据某挖泥船泥泵根据相似理论设计制造的，按照疏浚泥泵的设计原则，保证了叶片弯曲角度和流道形状满足相似性，模型泵模型如图1所示。为确保PIV能够拍摄叶轮内部的清晰图像，参照文献［10~12］，模型泵的泵壳和叶轮均采用透明有机玻璃制成，并将吸入口置于轴侧［10］，其主要设计参数如表1所示。模型泵由变频电机驱动，可调节频率设定泵转速。

图1 透明模型泵

表1 模型泵的主要参数

2.2 PIV系统

PIV系统的组成和工作原理如图2所示。

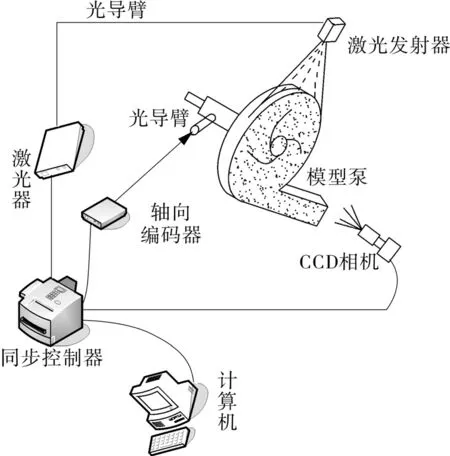
图2 PIV系统原理

激光从模型泵正上方垂直向下照射，为降低边壁效应，照射面处于叶轮宽度方向的中间。CCD相机镜头垂直于照射面，正对模型泵的非轴侧进行拍摄。泵轴相连的电机轴末端装有编码器，与PIV系统的同步控制器相连。在编码器中设定某一角度，每当叶轮旋转至这一角度时，均由编码器向同步控制器发出一个脉冲信号，同步控制器间隔极短的时间分2次向激光器和CCD相机同时发出触发命令，激光照射的同时进行拍摄，获得一对图像，对该图像对进行相关性分析即可获得叶轮内的流场信息。当试验系统内流动基本稳定后，叶轮旋转至相同角度时的流场趋于定常，此时将同一角度下拍摄的多幅图片平均处理，即可获得叶轮内水流或颗粒的运动趋势。

2.3 试验工况

本文选择疏浚中常见的砂土颗粒作为研究对象，分别对0.2~0.4 mm粒径的中砂和0.8~1 mm的粗砂颗粒进行了系列试验。由于PIV系统对颗粒的感光性、透光性等方面的要求，试验采用密度相近的玻璃珠代替砂土，玻璃珠密度为2.42 g/cm3。考虑到疏浚船舶上泥泵一般运行在400~600 r/min范围内，故试验中泵转速采用500 r/min。改变管路中的阀门开度可调节流量，流量参数依次选取为 1.25Q0、1.0Q0和 0.75Q0（Q0为该转速下输送清水时的最高效率点对应流量），通过管路中的电磁流量计可获得实时的流量。初步探索试验时发现即使采用透光性较好的玻璃珠代替泥砂颗粒，当颗粒浓度稍高时，激光照射面仍会受叶轮上半部分颗粒较大的影响，导致叶轮上下两部分颗粒的灰度值差异较大而无法同时识别，软件对下部流场无法进行有效的流速分析。故试验选取较低的体积浓度CV，分别为0.1%、0.5%和2%。试验时，观察管道内颗粒分布均匀且流量基本稳定后，即进行拍摄，每一工况拍摄100对图片，进行平均分析。同时作为比较基准，还在各流量下进行了相应的清水试验，此时采用粒径1~5 μm的示踪粒子反映流场信息。试验工况表如表2所示。

表2 试验工况表

3 试验结果与分析

PIV的图像处理可直接获得叶轮内的绝对速度流场，而研究颗粒对叶轮做功的影响，主要分析颗粒相对叶片的运动情况。根据颗粒和泵轴中心的位置，可算得颗粒处的叶轮轴向速度，结合所测绝对速度通过速度三角形即可计算出相对速度。将多对图像中颗粒的相对速度汇总显示，可反映颗粒在叶轮内运动的总体趋势。以0.1%浓度工况为例，该工况下不同流量下中砂和粗砂的相对速度场如图3所示。

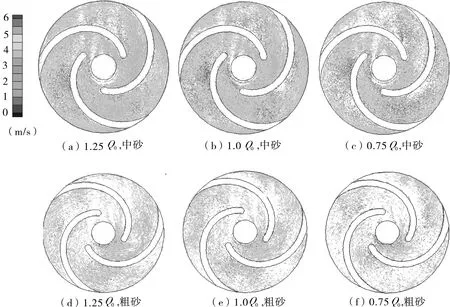
图3 颗粒相对速度场(CV=0.1%)

PIV系统可通过灰度值识别出颗粒，然后依据图像的相关性对各个颗粒计算其速度，即图中的速度点与颗粒一一对应，速度点的疏密程度反映了单位空间内的颗粒数含量。体积浓度相同时，中砂颗粒的数目较多，因此图中叶轮内中砂颗粒的速度点比粗砂颗粒分布更为密集。

从图可见，叶轮流道内颗粒的相对速度是变化的，尤其是中砂颗粒的速度场中，流道的前半段出现了速度较高的区域，而后半段出现了则低速区，且随着流量减小，颗粒在叶轮内运动的相对速度下降，低速区有向叶轮进口方向扩大的趋势。

为更直观地观察颗粒相对速度在流道内的变化，按照与泵轴中心距离线性递增的方式，沿流道中线选择6个点（见图4），读取各点的相对速度值，以CV=0.1%、Q=1.0Q0的工况为例，将清水、中砂和粗砂试验时该点的相对速度值对比显示在图4中。

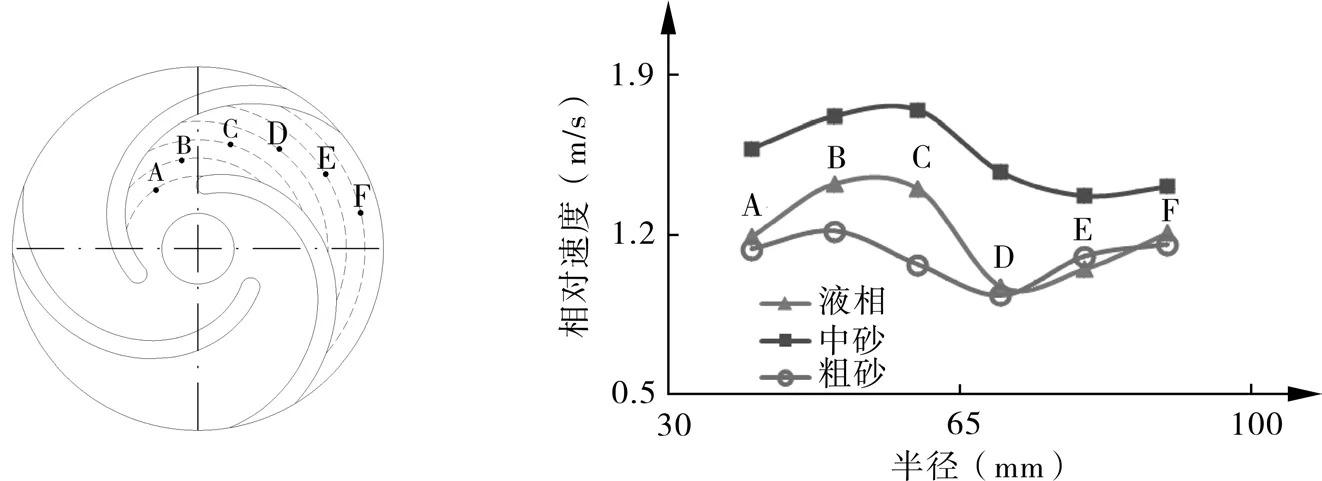
图4 流道内颗粒相对速度对比（CV=0.1%，Q=1.0Q0）

由图可知，流道内中砂颗粒和粗砂颗粒的相对速度值变化规律并不相同。从数值的变化幅度来看，中砂颗粒的变化与清水相似，均在流道前半段出现高速区，后半段出现低速区；而粗砂颗粒的相对速度值尽管也略有起伏，但变化幅度较小。这主要是由2种粒径颗粒的惯性不同引起的。旋转叶轮通过液相对颗粒传递作用，液相速度的变化必然会引起颗粒变速，粗砂颗粒质量大于中砂颗粒，惯性大，外界变化引起的加速度较小，故中砂颗粒对液相速度变化的响应快，与液相呈现相似的变化趋势，而粗砂颗粒的响应则较小。

另一方面，比较颗粒与液相的相对速度值，中砂颗粒在整个流道内的相对速度均高于液相，而粗砂颗粒的相对速度在流道前半段小于液相，后半段则与液体相近。根据文献［13］可知，中砂颗粒相对速度高于液相，会对过流通道产生“相对抽吸”作用，数量较大时会引起轴面运动速度降低，液相流动角减小，而粗砂颗粒则会对流动前半段产生“相对阻塞”作用，适当提高轴面运动速度，液相流动角有所增加。

2种泥砂颗粒运动的这种不同，是由其受到的外力决定的。颗粒在叶轮流道内的受力复杂，包括水下重力、离心力、液体粘性力、Basset力、附加质量力、Magnus力和Saff man力等［14］。其中，某些力只在特定情况下才会出现，且量级较小，而前5种力对颗粒的运动影响较大，是一般研究中主要考虑的颗粒作用力［15］。假设泥砂为直径ds的球形颗粒，颗粒和液体密度分别为ρs和 ρl，液相的动力粘度和运动粘度分别记作μ和ν，ws和wl分别表示固体颗粒和流体的相对速度，us为液相圆周速度，CD为液相绕流颗粒时的阻力系数，时间记作t，则上述主要作用力及其所引起的颗粒加速度可由表3中公式表示。

表3 颗粒所受主要作用力及其加速度计算式

上述作用力中，颗粒运动的驱动源自离心力，是由颗粒在液相裹挟下作圆周运动产生的，研究发现颗粒与液相在圆周方向的跟随性较好，为简化分析忽略其相对滑移。液相粘性力的方向与两相的相对速度差有关，当颗粒运动快于液相时，粘性力是颗粒运动的阻力，反之则对颗粒起挟带作用，两相速度接近时该作用力消失。Basset力是颗粒在粘性流体内发生速度变化时受到的瞬时阻力，与两相速度变化率的差值相关。附加质量力是液相推动颗粒周围流体随颗粒一起加速所需的附加力，是颗粒运动的阻力，也与两相速度变化率的差值相关。

分析加速度公式可获知改变颗粒运动的关键因素，中砂和粗砂的颗粒密度相同，区别在于粒径不同。从表中可以看出，离心力加速度与颗粒粒径无关，即相同转速下中砂和粗砂颗粒在同一位置处获得的驱动加速度一定，速度的改变主要取决于阻力。中砂颗粒与液相的跟随性好，两相速度变化率较接近，Basset力和附加质量力较小，主要由液相粘性力产生阻力与离心力进行平衡，故颗粒速度高于液相；粒径增加时颗粒惯性变大，固液两相的速度变化率差距加大，这会引起Basset力和附加质量力的加速度产生增加的趋势。粗砂颗粒的Basset力和附加质量力的加速度达到一定量级［16］，甚至高于离心力作用，需通过粘性力提供动力才能达到平衡，故在流道前半段，粗砂颗粒相对速度低于液相。而当Basset力和附加质量力的加速度与离心力加速度达到平衡时，两相的相对速度就相差不大，这可能是流道后半段粗砂颗粒相对速度与液相接近的原因。

4 结论

（1）中砂颗粒和液体的相对速度场均在流道前半段出现高速区，在后半段出现低速区，且流量减小时低速区面积增加并向进口方向扩大；与此相比，粗砂颗粒的相对速度变化幅度较小。

（2）在离心力的主要驱动下，中砂颗粒的相对速度值在整个流道内均高于液相，会对流道产生“相对抽吸”作用；粗砂颗粒运动的阻力增大，在流道前半段其相对速度值低于液相，会对流道产生“相对阻塞”作用，在流道后半段两相速度接近。

［1］ 倪福生, 杨年浩, 孙丹丹. 固液两相流泵的研究进展［J］. 矿山机械, 2006(2):67-69.

［2］ 程成，施卫东，张德胜，等． 后掠式双叶片污水泵固液两相流动规律的数值模拟［J］.排灌机械工程学报，2015，33(2) : 116-122．

［3］ 韩伟，岳婷，李仁年，等.基于大涡模拟的动静叶栅内固液两相流动［J］.排灌机械工程学报，2015，33(11) : 940-944．

［4］ 张立栋，杨梓，李伟伟,等. 低温省煤器入口联箱工质流动分析［J］.压力容器，2015,32(10)：30-36.

［5］ 北京立方天地科技发展有限责任公司.粒子图像分析系统MicroVec V2.3使用手册［Z］.2008.

［6］ Khalitov D A, Longmire E K. Simultaneous two-phase PIV by two-parameter phase discrimination［J］.Experiments in Fluids, 2002(32):252-268.

［7］ Jaikrishnan R K, Pathom C, Subramanian A, et al.Investigations of particle velocities in aslurry pump using PIV: Part 1, the tongue and adjacent channel flow［J］. Journal of Energy Resources Technology,2004(126):271-278.

［8］ 崔巧玲. 固相参数对泵内流动影响的数值模拟与PIV测试［D］.杭州：浙江理工大学,2012.

［9］ 李昳.离心泵内部固液两相流动数值模拟与磨损特性研究［D］.杭州:浙江理工大学,2014.

［10］ 杨敏官,刘栋,顾海飞,等.盐析液固两相流场的PIV测量方法［J］.江苏大学学报(自然科学版),2007, 28(4):324-32.

［11］ 郎涛, 施卫东, 陈刻强,等.前伸式双叶片污水泵内部流场PIV试验［J］. 农业工程学报, 2015,31(20):74-79.

［12］ 刘明星,倪福生,汤雷,等.疏浚泥泵小流量工况下的PIV试验［J］. 流体机械, 2015, 43(7): 6-9.

［13］ 蔡保元.水力机械内的固液二相流设计新理论［J］.工程热物理学报, 1991, 12(3):261-266.

［14］ Sellgren A. Performance of a centrifugal pump when pumping ores and industrial minerals［C］. Proceedings of 6th International Conference on the Hydraulic Transport of Solids in Pipes, 1979: 291-304.

［15］Burgess K E, Reizes J A. The effect of sizing,specific gravity and concentration on the performance of centrifugal slurry pumps［J］. Proceedings of the Institution of Mechanical Engineers, 1976, 190(1):391-399.

［16］ 李昳.离心泵内部固液两相流动数值模拟与磨损特性研究［D］.杭州:浙江理工大学,2014.