基于灰关联分析和粗糙集的通信电台识别方法*
史健,蒋建中
(解放军信息工程大学,郑州450000)
基于灰关联分析和粗糙集的通信电台识别方法*
史健,蒋建中
(解放军信息工程大学,郑州450000)
通信侦察过程积累了大量电台通信记录,对这些数据进行分析、推理,可以识别电台的数量、装载平台等,为了提高识别正确率,提出了基于灰关联分析和粗糙集的通信电台识别方法。首先,依据粗糙集理论将信息表划分等价类,得到电台航迹;再根据灰关联分析计算雷达航迹和电台航迹的灰关联度,最后按照最大灰关联度原则进行通信电台关联。实验结果表明该方法适用范围更广,在多个平台的运动轨迹交叉且在交叉时刻各有电台通联、同一平台上的多个电台在不同时间通联这两种情况下,均能较好地对电台进行关联。
电台识别,通信对抗,数据关联,灰关联分析,粗糙集理论
0 引言
通信电台识别是通信电子战中的重点、难点内容。对通信电台型号、数量、装载平台及网台种类等进行识别,是分析敌军行动意图和战场态势的前提。然而通信信号技术参数与通信电台之间的关系、通信电台与其装载平台之间的关系均不够明确,有时它们相互之间甚至没有清晰的对应关系[1]。如何处理大量的、杂乱无章的无线电信号数据,成为通侦信息融合的首要问题。文献[2]将粗糙集理论用于通信电台及其装载平台的识别,按照中心频率、调制方式、带宽等属性对电台通信记录进行划分。划分到等价类中的记录,被认为来自于同一电台。然后根据电台的三维坐标,判断哪些电台在同一平台上,再根据平台上电台数量初步判断该平台的类型,文中给出装载平台的判断规则如下:
①若地面平台的电台数量大于等于4个,则该平台是指挥所;
②若空中平台的电台数量大于3,则该平台是预警机,否则是战斗机;
③若空中平台的电台功率大于400 W,且电台数量小于3,则该平台是电子战飞机。
文献[3-4]对原始侦察数据作预处理后,同样采用粗糙集的方法进行电台识别。粗糙集理论已经成功应用于通信电台及其装载平台的识别。然而上述文献中利用三维坐标判断电台数量的方法仍存在弊端,原因有:①目前无线电台定位精度不够高,尤其短波定位误差较大;②如果两个或多个平台的航迹交叉,在交叉点处又恰好都有通信电台发出电磁信号,那么势必会造成电台数量的误判;③对于同一移动平台上的不同电台,当它们在不同的时间出联时,无法判断它们是否来自同一平台。
对此,文献[5]提出对电台航迹进行聚类,属于同一类的电台被认定在同一装载平台上,由此来判断平台上的电台数量,该方法在一定程度上弥补了文献[2-4]中方法的不足。但是在电台航迹交叉以及电台出联时刻相距较长时,对电台航迹聚类的方法也存在较大误差。
因此,本文提出一种新的改进方法,将电台航迹与雷达航迹进行关联,与同一雷达航迹关联的电台被认为处在相同的平台,以此来判断平台上的电台数量。为叙述方便,本文将通过雷达测量的平台运动轨迹称作雷达航迹(以方位角表示);将根据电台信号测得的电台运动轨迹称作电台航迹(以方位角表示)。理论上,如果某电台搭载在某个平台上,那么该电台航迹与雷达航迹是重合的,所以在同一时间内,只要电台航迹与雷达航迹足够接近,就认为该电台搭载在该平台上。
雷达航迹与电台航迹的关联,即确定电台信号究竟源于哪一个雷达目标,本质上是模式识别问题。假设在t1~t2时间内,发现n个电台信号,它们的航迹分别是radio1,radio2,…,radion;该段时间内测得雷达目标有m个,它们的航迹分别是radio1,radio2,…,radiom。那么上述航迹关联问题就简化为将radioi(i=1,2,…,n)划分到类radioj(j=1,2,…,m)中。本文采用的划分方法是灰关联分析,把radioi(i=1,2,…,n)划分给与其关联度最大的类。
仿真实验表明,本文方法可以克服文献[2-5]方法的不足。多个平台在同一时刻经过同一点,且在该时刻都有电台通联的情况下,本文方法不会将来自不同平台的电台关联在一起(图5中电台D和电台G便是此情形下的一个例子);同一平台上的几个电台即使在不同时间通联,本文方法也可以将这些电台正确地关联在一起(见第32页图5中电台A、B、C和D)。
1 基本概念
本文根据粗糙集理论进行等价类划分,得到电台航迹。但是与文献[2-4]中按照电台三维坐标划分等价类并进行电台关联的做法不同,本文方法在得到电台航迹后,采用灰关联分析理论对电台航迹与雷达航迹作灰关联分析,以此进行电台关联。下面对文中涉及的基本概念作粗略的介绍。
1.1 粗糙集
粗糙集(Rough Set)理论[6]是一个处理模糊和不确定数据的数学工具,在数据挖掘、模式识别、专家系统等领域应用广泛。粗糙集与证据理论、模糊集等理论相比,其最大的特点是不需要任何的先验信息,它不需要基本概率分配函数、不需要隶属度函数,仅根据数据本身便可以对数据进行处理。
应用粗糙集理论之前,需要把数据组织成信息表形式。信息表是一个表格,它的行表示对象(object),列表示属性(attribute),全体对象的集合称为论域(一般用U表示)。表1便是一个信息表的例子[7]。

表1 信息表
表1中共有4个对象(patient1,patient2,patient3,patient4)、4个属性(headache,muscle_pain,temperature,flu),其中flu被称作决策属性,其他3个属性称作条件属性。粗糙集中的主要概念是不可分辨关系(indiscernibility relation),它通常由一系列属性组成。例如属性headache和muscle_pain组成不可分辨关系r1,在此关系下,对象patient1、patient2、patient3的取值相同,也就是说它们之间是不可分辨的,此时认为3个对象等价。关系r1在论域U上产生一个划分,即U/r1={{patient1,patient2,patient3},{patient4}},其中{patient1,patient2,patient3}和{patient4}称作等价类,等价类中的对象是等价的。
1.2灰关联分析
灰关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密,曲线越接近,相应序列之间关联度就越大,反之就越小[8]。
假设有序列Xi=(xi(1),xi(2),…,xi(k),…,xi(n)),k=1,2,…,n,如果k为时刻,则Xi称为时间序列;如果k表示指标,则Xi称为指标序列;如果k表示对象,则Xi称为横向序列。无论是时间序列、指标序列还是横向序列,都可以用来作关联分析。此外,灰关联分析中还定义了几个算子,其中常用到的是区间值化算子。
定义1假设有序列Xi=(xi(1),xi(2),…,xi(n)),D为序列算子,且
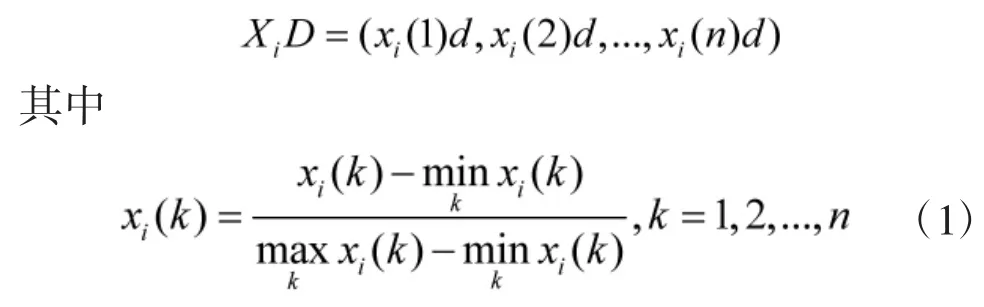
则称D为区间值化算子。
区间值化算子可以使序列无量纲化,且在数量上归一。因此,常用于序列数据的预处理。
设有序列Xi=(xi(1),xi(2),…,xi(n)),i=0,1,…,m,选取X0作为参考序列,Xi(i=0,1,…,m)为比较序列,那么X0与Xi的灰关联度为:
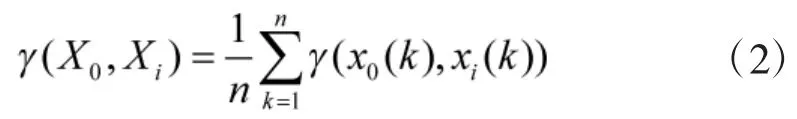
其中,
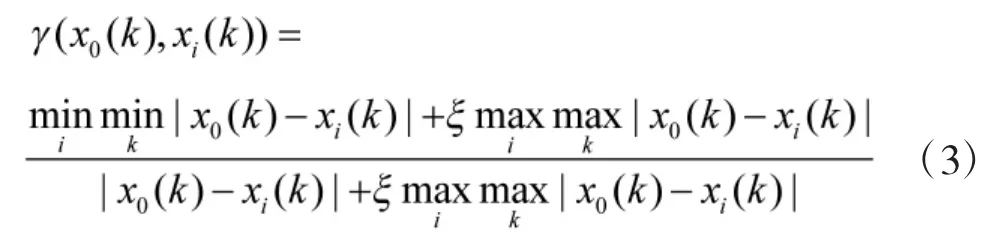
式(2)和式(3)中

得到灰关联度后,按照最大关联度准则,选择与X0最相近的序列。
2 基于数据关联的电台识别方法
2.1 数据处理
经过长期积累,数据库中保存了大量侦察数据,在进行分析之前要对这些数据作一些处理,这些处理包括:
(1)把数据组织成信息表形式。
把数据库中每条电台侦察记录视作一个对象,将中心频率、调制方式、带宽、截获时间等技术参数视作属性,得到如下信息表。
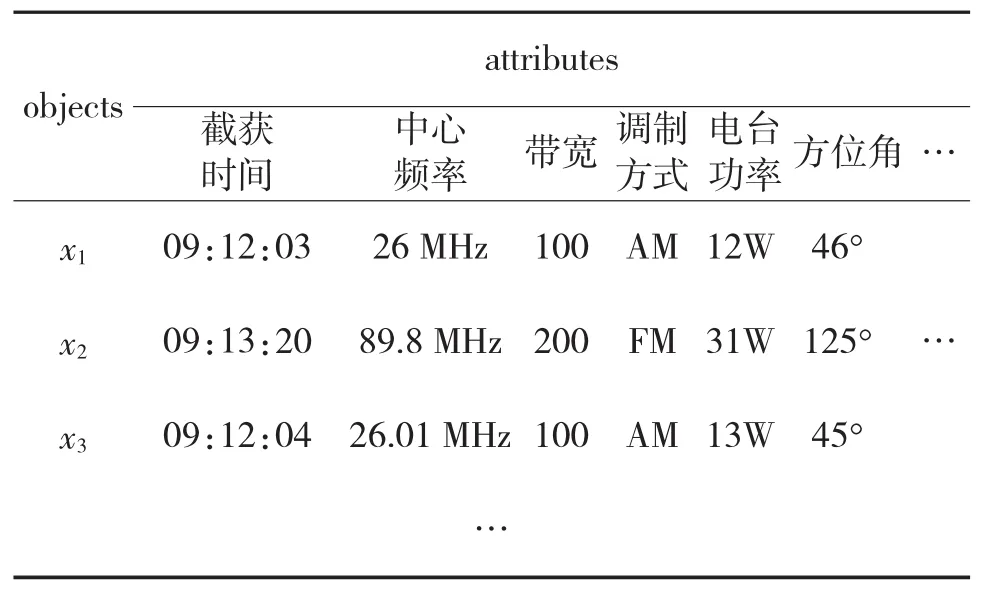
表2 通信侦察数据信息表
(2)定义不可分辨关系,然后用不可分辨关系对论域进行划分,求得电台航迹。
不可分辨关系定义为R={中心频率,调制方式,带宽,…},R将论域U划分成不同等价类,每个等价类代表一部电台通信记录。更详细的描述参见文献[2-3]。
经过关系R划分后得到电台库,根据电台库可以求得电台航迹。例如表2中论域U={x1,x2,x3},经过关系R划分后得到等价类{x1,x3}和{x2},则电台库为{电台A,电台B}。等价类{x1,x3}表示电台A在不同时刻被侦察到两次,那么电台A的航迹记作(46°,45°),等价类{x2}表示电台B的侦察记录,那么电台B的航迹可以记作(125°)。
(3)统一坐标系与参考点,利用式(1)除去量纲。
如果雷达与ESM设备处于同一平台,它们测量的方位角信息是一致的。若雷达和ESM设备异地配置,它们测量的方位角信息不一致。如图1所示。

图1 雷达和ESM设备侦测示意图
雷达和ESM设备测得目标方位角分别是θr和θe。根据文献[9],假设雷达测量目标的距离为L,则目标的直角坐标为

转换成以ESM设备为参考点后,目标的方位角为

(4)对雷达航迹进行曲线拟合。
由于雷达扫描周期比ESM扫描周期长,所以在相同时间内两者的航迹点数是不相等的。又因为计算灰色关联度时要求序列等长,所以必须将雷达航迹与电台航迹的数据点对齐,即补齐雷达航迹在某些时刻的值,本文采用的方法是对雷达航迹进行曲线拟合,得出雷达航迹的方程,然后求取相应时刻雷达航迹的值。
2.2 雷达航迹与电台航迹关联
一个雷达目标航迹对应一个目标,一个电台航迹对应一个辐射源,且一个目标可以载有多个辐射源,因而一个雷达目标航迹可以和多个电台航迹关联,而一个电台航迹至多可以和一个雷达目标航迹关联[10]。

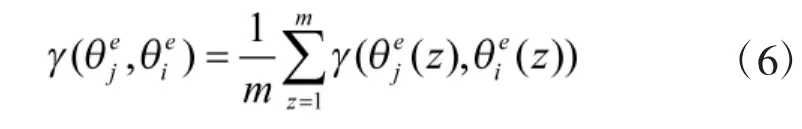
其中,

S4:如果已经遍历电台航迹库,转到S5,否者转到S1;
S5:与同一个雷达航迹关联的电台被认为在相同的平台上;
S6:结束。
3 实验仿真
设雷达扫描周期为5 s,雷达测角误差服从正态分布N(0,0.3),测距误差服从正态分布N(0,150),雷达坐标(20,0);ESM侦测设备扫描周期为1 s,测角误差服从正态分布N(0,1),坐标(0,0);平台运动速率不变。
在时间T内,有3个空中平台,在直角坐标系中,其运动轨迹如图2所示,雷达测得的目标轨迹如图3所示:
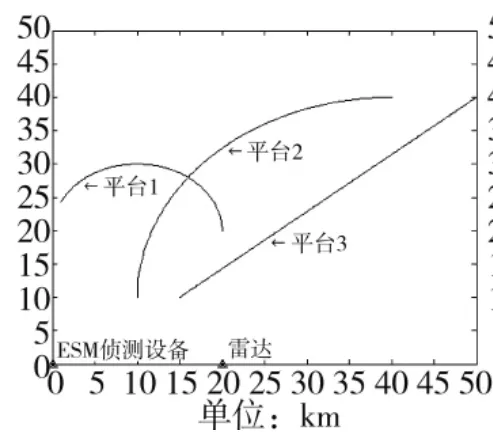
图2 平台的真实运动轨迹

图3 雷达测得的平台运动轨迹
利用式(4)和式(5),把图3所示的二维坐标点转换成以ESM设备为参考点、以方位角表示的航迹,即上文所述雷达航迹,雷达航迹见图4。经过2.1节数据处理后,得到电台航迹如图5所示。
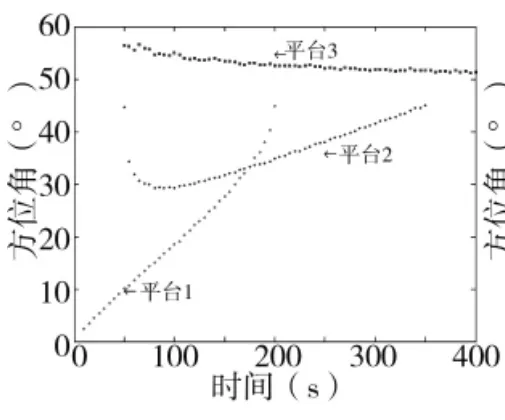
图4 雷达航迹
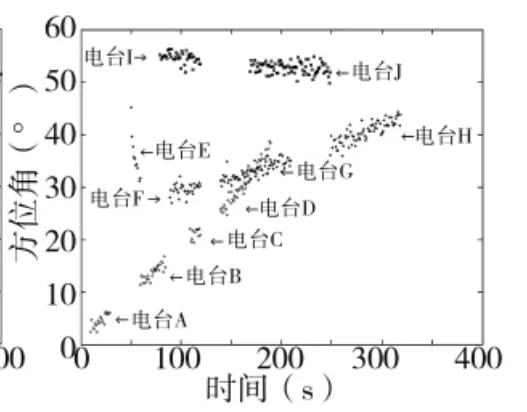
图5 电台航迹
将电台A的电台航迹与所有雷达航迹进行灰关联分析,由于电台航迹与雷达航迹的点数不一致,需用最小二乘方法对雷达航迹作曲线拟合。计算电台A的电台航迹与所有雷达航迹的灰关联度。关联结果如下页表3所示。
阈值α取0.85,根据最大关联度准则,判决结果为:电台A、B、C、D与平台1关联,电台E、F、G、H与平台2关联,电台I、J与平台3关联。根据文献[3]给出的装载平台判断规则,可知电台A、B、C、D、E、F、G和H的装载平台都是预警机,电台I和J的装载平台可能是战斗机或者电子战飞机,若要知道该平台更详细的描述,可以根据粗糙算子作进一步的判断[2,11]。
如果按照文献[2-4]的方法计算,在电台B与电台D航迹交叉的地方会造成关联错误;按照文献[5]的方法,电台A、B、C和D的航迹相距较远,它们并不能聚在同一类,因此,不能判断电台A、B、C和D装载在同一个平台上。
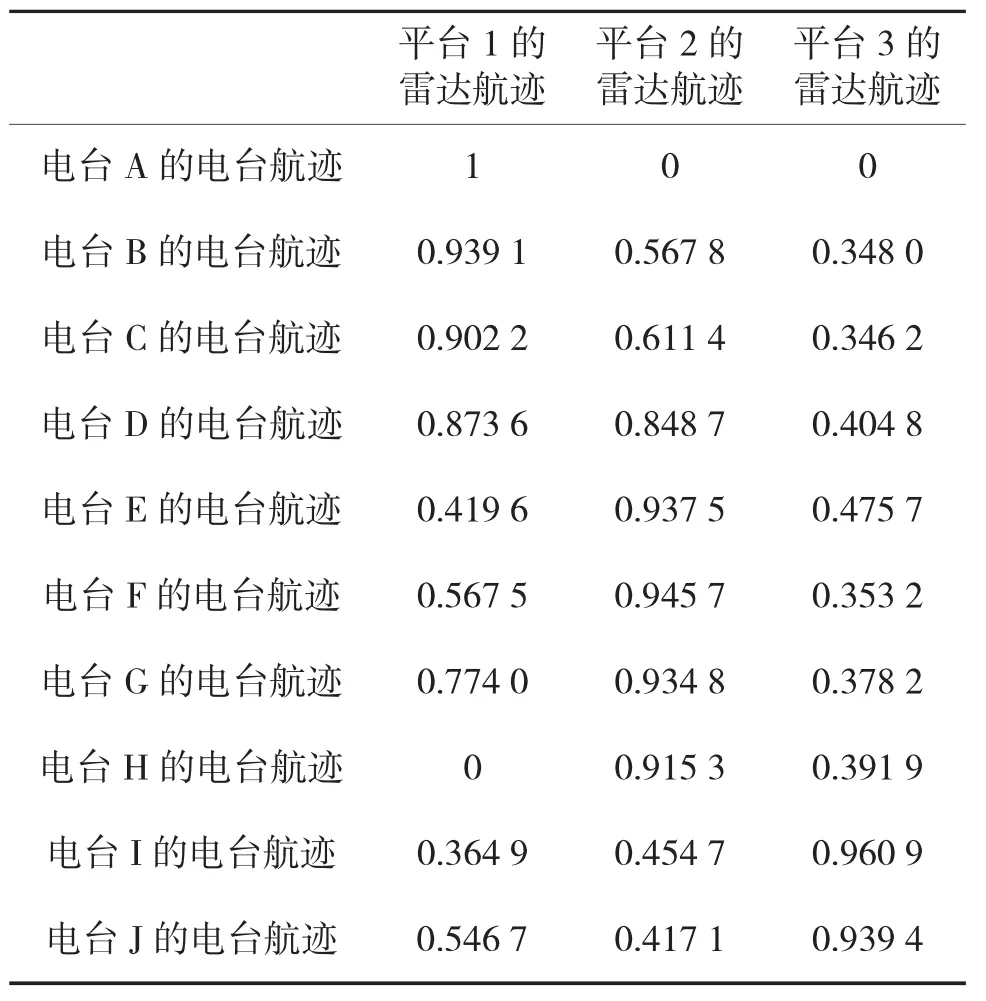
表3 电台航迹与雷达航迹的关联度
4 结论
通信侦察产生大量电台通信数据,如何对它们进行分析和挖掘是通侦信息融合的重要内容。对雷达和电台数据进行融合,可以充分利用不同类型传感器的特点,实现对目标更透彻的理解。因此,本文利用粗糙集理论进行等价类划分得到电台航迹后,把电台航迹与雷达航迹进行关联。实验分析结果表明,在多个平台的运动轨迹交叉且在交叉时刻各有电台通联、同一平台上的多个电台在不同时间通联这两种情况下,本文方法均能较好地对电台进行关联。
[1]徐从富,潘云鹤.通侦信息智能化融合系统(TFS/CI2)[J].电子与信息学报,2002,24(10):1358-1365.
[2]徐从富.基于粗糙集理论的通信电台及其装载平台识别[J].计算机工程与应用,2002,38(10):221-226.
[3]任重,邵军力.粗糙集理论在通侦信息融合中的应用[J].解放军理工大学学报(自然科学版),2002,3(6):96-99.
[4]李晶莹,钟子发,范瑞星.基于粗糙集理论对多传感器侦察数据初级融合处理[J].通信技术,2009,42(11):104-107.
[5]金栋,文志信,吴天昊.DBSCAN算法在通信电台关联上的应用[J].舰船电子工程,2011,31(6):76-79.
[6]PAWLAK Z.Rough sets[J].International Journal of Computer and Information Sciences,1982,11(5):341-356.
[7]PAWLAK Z,GRZYMALA-BUSSE J,SLOWINSKI R,et al. Rough sets[J].Communications of the ACM,1995,38(11):89-95.
[8]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].3版.北京:科学出版社,2004:50-72.
[9]宋振宇,张翔宇,张光铁.系统误差对异地配置的雷达和ESM航迹关联影响[J].电光与控制,2014,21(3):42-46.
[10]何友,王国宏,陆大幺灬金,等.多传感器信息融合及应用[M].北京:电子工业出版社,2000:167-170.
[11]蒋云良,徐从富,邵斌.基于Rough Set理论的推理机制的研究[J].计算机应用研究,2004,21(9):110-112.
A Method of Communication Station Recognition Based on Grey Relational Analysis and Rough Set
SHI Jian,JIANG Jian-zhong
(Information Engineering University,Zhengzhou 450000,China)
Analysing data of communication reconnaissance will help to recognise the quantity and platform of communication stations.A method of communication station recognition based on grey relational analysis and rough set is proposed for the purpose of enhancing accuracy.Firstly,information table is divided by indiscernibility relation according to rough set theory to obtain communication station tracks;Then gray relational degreesbetween radar tracks and radio station tracks are computed;Finally,corelation of communication stations is analysed according to maximum gray relational degree principle.The experiment result shows that this method has good performance,particularly inthe following two cases:radio stations are sending signalsnear the junction of their trajectories and radio stations from the same platform work at different time periods.
radio station recognition,communication countermeasures,data correlation,grey relational analysis,rough set theory
TP391.4
A
1002-0640(2017)02-0029-05
2016-01-11
2016-02-27
国家自然科学基金资助项目(61104036)
史健(1990-),男,辽宁葫芦岛人,硕士研究生。研究方向:通信信号分析与处理,人工智能。

