改进的正弦余弦算法在函数优化问题中的研究
张校非,白艳萍,郝 岩,王永杰
(中北大学 理学院,太原 030051)
改进的正弦余弦算法在函数优化问题中的研究
张校非,白艳萍,郝 岩,王永杰
(中北大学 理学院,太原 030051)
正弦余弦算法(SCA)是2015年提出的一种新型的群智能算法。针对标准正弦余弦算法局部搜索能力差、精度低的缺点,提出改进的正弦余弦算法(简称ISCA)。首先,引入动态惯性权重平衡算法的局部与全局搜索能力;然后,为更进一步加强迭代后期局部搜索能力,将参数r1由线性递减函数变成了指数型递减函数;最后,引入自适应变异因子,增强种群的多样性;最后,将改进的SCA算法对10个经典的单峰、多峰函数进行测试,并同标准SCA算法、粒子群算法(PSO)、遗传算法(GA)进行比较。实验结果表明:ISCA算法优于其他几种算法。
正弦余弦算法;动态惯性权重;指数递减参数;自适应变异因子;函数优化
目前,用群智能算法解决优化问题是一个十分活跃的研究领域[1],而用于解决优化问题的群智能算法有很多,如遗传算法(GA)[2]、粒子群算法(PSO)[3-4]、人工蜂群算法(ACO)[5-7]、果蝇算法(FOA)[8-11]等。正弦余弦算法(SCA)[12]是一种新型的元启发试算法,它是建立在正弦余弦函数上的自组织和群智能基础上的数值优化计算方法。最先由Seyedali和 Mirjalili提出了正余弦概念的自组织模型。通常来说,群优化技术开始于一组随机解,这个随机解通过一个目标函数反复被评估,并且通过一组规则来提高,这是优化技术的核心。因为基于群的优化技术随机寻找优化问题的最优解,所以不能保证再一次运行中找到最优解。然而,通过足够的随机解和优化迭代,能够大大增加找到全局最优解的可能性。
虽然SCA算法具有较强的全局搜索能力,但局部搜索能力较差。本文提出的改进的SCA算法是为了进一步加强标准SCA算法的局部搜索能力,提高算法精度以及减少早熟、过学习的发生。通过引入动态惯性权重,平衡了局部搜索和全局搜索的过程;在算法中引入自适应变异因子,增加了种群的多样性;又将参数r1变为指数递减函数,增强了其后期的局部搜索能力。最后,将改进的SCA算法在函数优化问题上进行了仿真实验。
1 标准的正弦余弦算法(SCA)
标准的SCA算法是由澳大利亚学者Seyedali和 Mirjalili于2015年提出。算法始于一组随机解,通过搜索和开发阶段不断逼近全局最优解。首先,初始化解的位置,算法更新如式(1)所示:
(1)

(2)

如式(1)所示,在SCA算法中有4个主要参数,分别是r1,r2,r3和r4。参数r1决定了下一个位置的区域(或移动方向),它既可以是当前解和目标解之间的区域,也可以是二者之外的区域;参数r2定义了当前解应该朝目标解或远离目标解的距离;参数r3为目标解随机地赋予一个权值,目的是加强(r3>1)或削弱(r3<1)所定义的距离对目标解的影响;参数r4使式(1)中的正余弦的组成部分均等转换。
图1表明了当r1取不同值范围时,解的搜索区域。

图1 不同r1值对解搜索区域的影响
图1只说明了一个二维模型,应该注意的是这个模型可以扩展到更高的维度。正弦余弦函数的循环模式允许一个解在其他解的周围被重新复位,这能保证在两个解之间的空间进行搜索。对于搜索空间,解应该能够同时搜索到它们相关的目标点之间的空间外侧, 这是通过改变正弦余弦函数的范围来实现的,如图2所示。

图2 在区间[-2,2]的正弦余弦函数Fig.2 Sine cosine function in interval[-2,2]
一个范围在[-2,2]的正弦余弦函数的概念模型如图3所示。表明无论怎样改变正弦和余弦函数的范围,在这个解和其它解之间都需要一个解在空间内部和外部更新它的位置。在等式(1)中的内、外部随机位置通过定义一个范围在[0,2π]的随机数来实现。因此,这种机制保证了搜索空间的搜索和开发。
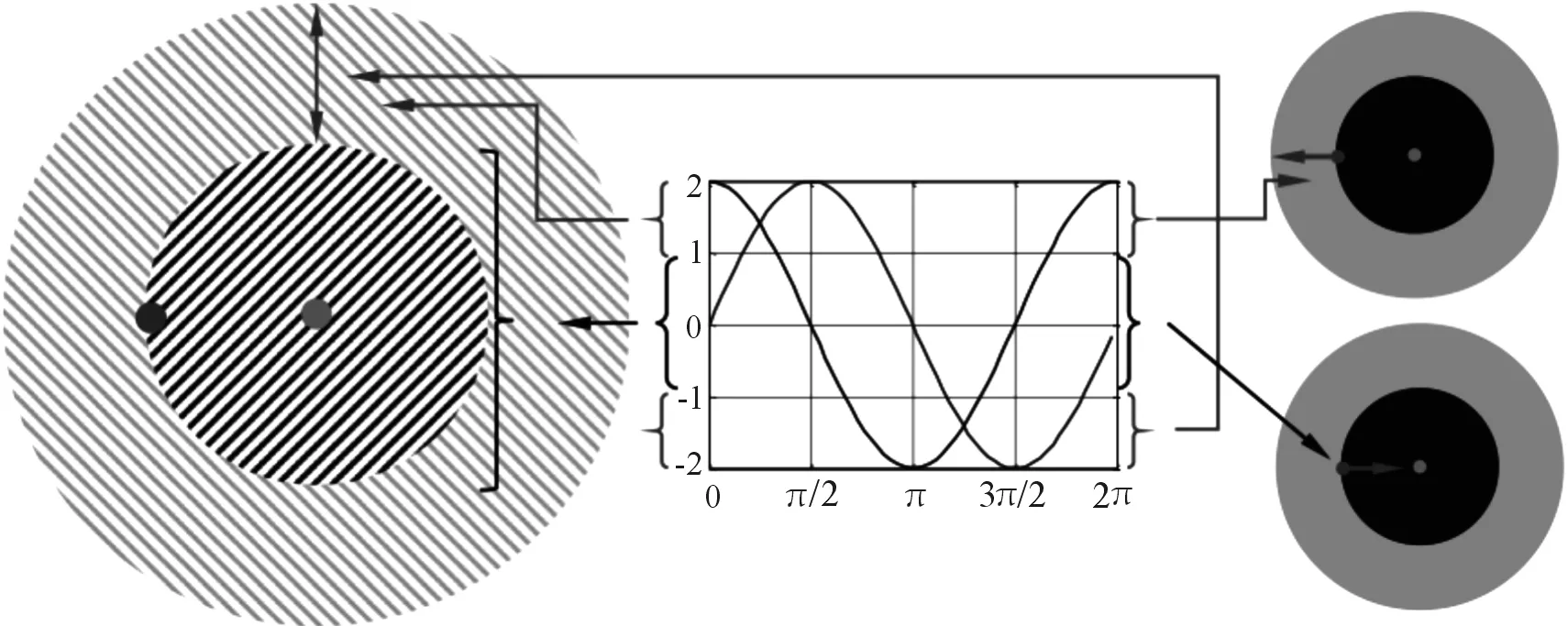
图3 在当前解和目标点的内部和外部区域
图4显示了在式(1)迭代过程中如何降低正、余弦函数的范围。从图3和4中可以看出:当正余弦函数的区间范围在(1,2]和[-2,-1)上时,SCA算法搜索搜寻空间;当区间范围在[-1,1]上时,算法开发搜索空间。
经过以上操作,SCA算法能在理论上得到优化问题的全局最优解,主要有以下原因:
1) 对于一个问题,SCA提高了随机解的质量,与基于个体的算法相比,它本质上得益于较强的搜索能力和避免局部最优的能力。
2) 当正弦和余弦函数的返回值大于1或小于-1时,将搜索不同的空间区域。
3) 当正余弦值在[-1,1]时,期望的搜索空间区域被开发。
4) SCA算法从搜索到开发将进行平滑的过度,使用恰当的正余弦函数的范围。
5) 最接近全局最优的解作为目标点被储存在变量中,并且在优化过程中不会丢失。
6) 由于该解能随时更新当前在它周围得到最优解的位置,在优化过程中搜索空间有一个朝向最优区域的趋势。
7) 由于提出的算法将优化问题视为一个黑箱子,它可以很容易地结合不同领域的问题。

图4 递减的正弦余弦模式
2 改进的正弦余弦算法
2.1 动态惯性权重
经研究发现:惯性权重体现的是粒子位置多大程度上继承先前的位置。如果保持惯性权重不变,粒子在搜索的后期非常容易发生震荡。为了更好地平衡算法的全局搜索与局部搜索能力,本文在式(1)的基础上提出了线性型递减的惯性权重即:
w(t)=w0×(1.1-t/T)
(3)
式中,w0=1,w(t)为第t次迭代的惯性权重。随着迭代的进行,惯性权重从1.1递减到0.1,迭代初期保持了较强的搜索能力,而到了后期较小的惯性权重加强了局部开发,使解的搜索更精确。更新后的式(1)如式(4)所示:
(4)
2.2 指数型递减参数r1
为了进一步加强迭代后期局部搜索能力,将参数r1由线性递减函数变成了指数型递减函数即:
(5)
一般来说,r1start=0.9、rend=0.4时,算法性能最好。
2.3 自适应变异
SCA优化算法收敛快、结构简单,具有很强的通用性,但同时存在搜索精度低、容易早熟收敛、后期迭代效率低等缺点。本文借鉴了遗传算法中的粒子变异的思想,将变异算子引入SCA算法中,即以一定的概率对粒子进行初始化。变异操作扩大了在迭代过程中不断减少的搜索空间,使粒子可以跳出先前搜索到的最优值位置,保持了种群的多样性。其基本思想是粒子每次更新之后,以一定的概率重新初始化粒子,Matlab代码如下:
if rand>0.5
k=ceil(2*rand);
ifk== 1
X(i,k) =(20-1)*rand+1;
else
X(i,k)=(Xmax-Xmin)*rand+Xmin;
end
end
其中,Xmax、Xmin分别是粒子位置坐标的上界和下界;rand表示在(0,1)之间的随机数;X(i,k)表示第i个粒子在第k维搜索空间中的位置。
2.4 改进SCA算法流程
算法中每个粒子对应一个解,寻优过程如下:
步骤1 初始化解集xij,i=1,2,…,N,j=1,2…,D,其中N为粒子的数量,D为粒子维数。
步骤2 计算粒子的适应度找出全局最优。
步骤3 根据式(4)对粒子进行更新。
步骤4 以一定的概率重新初始化粒子;
步骤5 检查粒子的范围是否超出边界。若是,则把上界的值赋给大于上界的值,把下界的值赋给小于下界的值。反之,不作处理。
步骤6 判断当前粒子的适应度是否优于之前种群的全局最优解。若是,将当前的粒子的适应度值替换为全局最优解,反之,则返回步骤3;
步骤7 如果t 3.1 测试函数及算法参数设置 为了检验改进的SCA算法的性能,本文选用10个典型的测试函数进行数值实验。将改进的SCA算法与标准SCA算法进行比较,来测试改进后的SCA算法的效果和可行性。表1列出了10个测试函数,其中f1~f7为单峰函数,f8~f10为多峰函数。算法参数设置的表达式、维数、解初始范围、最优解如表1。 3.2 仿真实验 种群规模固定为30,迭代次数固定为1 000,算法运行30次。首先,对比 SCA 和 ISCA 的函数优化效果。实验选取了3个经典高维单峰函数和3个经典高维多峰函数。二者的收敛效果见图5;其次,选取表1的10个经典函数,分别从均值(ave)、方差(std)评估了ISCA的收敛精度,并与同类研究参考文献中标准的SCA算法、粒子群算法(PSO)、遗传算法(GA)相比较,结果见表2。 从图5(a)~(c)可以看出:对于单峰函数,ISCA在收敛精度和收敛速度上都远优于SCA。从图5(d)~(f)可以看出:对于某些多峰函数,两种算法的收敛精度近似,但ISCA收敛速度明显快得多。而对于另外一些多峰函数,ISCA的收敛精度和速度均有着明显的优势。 从表2中可以看出:对于单峰函数和多峰函数,ISCA无论是在收敛能力还是稳定性上,都优于其它3种群算法,这得益于其较强的跳出局部最小值的能力。观察表2中最后一行可以发现:ISCA算法中这10个测试函数的累积均值和累积标准差分别为2.1×10-4和9.875×10-5,而其他3种算法分别为9.51×10-3和1.05×10-3、7.88×10-1和1.56、5.19和3.995,说明该算法具有广泛的适用性。 表1 测试函数的基本信息 表2 4种算法的平均值和标准差 图5 函数 f1~f3、f8~f10在SCA和ISCA算法的收敛趋势比较 本文在原有SCA算法的基础上对其进行了的改进。通过引入动态惯性权重、改变参数r1的函数表达式、引入自适应变异因子等方式,使算法在寻优过程中不仅保持了较强的全局搜索能力,而且加强了其局部搜索能力,且丰富了种群的多样性。同其它的群智能算法相比,ISCA算法具有更好的收敛速度及精度,且适应性、稳定性更强。然而,该算法也有一些不足,比如在某些多峰函数中搜索精度不高,这些方面有待今后重点研究。 [1] 胡中功,李静.群智能算法的研究进展[J].自动化技术与应用,2008,27(2):13-15. HU Zhonggong,LI Jing.Research progress of swarm intelligence algorithms[J].Automation techtechnology and Application,2008,27(2):13-15. [2] 马永杰,云文霞.遗传算法研究进展[J].计算机应用研究,2012,29( 4):1201-1206. MA Yongjie,YUN Wenxia.Research progress of genetic algorithm[J].Computer applicationr research,2012,29(4):1201-1206. [3] KENNEDY J.Particle swarm optimization[M].New York:Springer,2011. [4] 梁军,程灿.改进的粒子群算法[J].计算机工程与设计,2008,29(11):2893-2896. LIANG Jun,CHENG Can.Improved particle swarm optimization algorithm[J].Computer engengineering and design,2008,29(11):2893-2896. [5] KARABOGA D.An idea based on honey bee swarm for numerical optimization[R].Technical report-tr06,Erciyes university,engineering faculty,computer engineering department,2005. [6] 郑伟,刘静,曾建潮.人工蜂群算法及其在组合优化中的应用研究[J].太原科技大学学报,2012,31(6):467-471. ZHENG Wei,LIU Jing,ZENG.Jianchao.Research on artificial bee colony algorithm and its appapplaication in combinatorial optimization[J].Journal of Taiyuan University of Science and TecTechnology,2010,31(6):467-471. [7] 王慧颖,刘建军,王全洲.改进的人工蜂群算法在函数优化问题中的应用[J].计算机工程与应用,2012,48(19):36-39. WANG Huiying,LIU Jianjun,WANG Quanzhou.Application of improved artificial bee colony algoralgorithm in function optimization[J].Computer engineering and ApplApplication,2010,31(6):467-471. [8] PAN W T.A new fruit fly optimization algorithm:taking the financial distress model as an example[J].Knowledge-Based Systems,2012,26:69-74. [9] 段艳明,肖辉辉.求解TSP问题的改进果蝇优化算法[J].计算机工程与应用,2016,52(6):144-149. DUAN Yanming,XIAO Huihui.Improved fruit fly optimization algorithm for solving TSP proproblem[J].Computer engineering and Applications,2016,52(6):144-149. [10]杨立君,付雅琴,殷旅江,等.一种改进的果蝇优化算法求解连续函数优化问题[J].湖北汽车工业学院学报,2016,30(1):71-74. YANG Lijun,FU yanqin,YIN Lvjiang,et al.An improved optimization algorithm for the the optimization of fruit fly optimization algorithm for continuous function optimoptimization[J].Journal of Hubei automobile and automobile industry collecollege,2016,30(1):71-74.[11]徐富强,陶有田,吕洪升.一种改进的果蝇优化算法[J].苏州大学学报(自然科学版),2014,29(1):16-23. Xu Fuqiang,Tao Youtian,LV Hongsheng.An improved fruit fly optimization algorithm[J].JourJournal of Soochow University(NATURAL SCIENCE EDITION),20142014,29(1):16-23.[12]MIRJALILI S.SCA:A Sine Cosine Algorithm for solving optimization problems[J].Knowledge-Based Systems,2016,96:120-133. (责任编辑 陈 艳) Research of Improved Sine Cosine Algorithm in Function Optimization ZHANG Xiao-fei, BAI Yan-ping, HAO Yan, WANG Yong-jie (School of Science, North University of China, Taiyuan 030051, China) The sine cosine algorithm (SCA) is a new kind of swarm intelligence algorithm which was proposed in 2015. In view of the poor local search capability and low precision of the standard sine cosine algorithm, an improved sine cosine algorithm (ISCA) was proposed. Firstly, we introduced dynamic inertia weight and balance the algorithm of local and global search ability; and the, we further strengthened the late iterative local search ability, and made parameters R1 turn from linear decreasing function into the exponential decreasing function; thirdly, we introduced self-adaptive mutation factor to enhance the diversity of the population. Finally, the improved SCA algorithm was tested on 10 classical single peak and multimodal functions, and compared it with standard SCA algorithm, particle swarm optimization (PSO) and genetic algorithm (GA). Experimental results show that the ISCA algorithm is better than other algorithms. sine cosine algorithm; dynamic inertia weight; exponential decline parameter; adaptive mutation factor; function optimization 2016-10-12 基金项目:国家自然科学基金资助项目(61275120) 张校非(1991—),男,硕士研究生,主要从事现代优化算法、神经网络在组合优化中的应用研究,E-mail:598095564@qq.com。 张校非,白艳萍,郝岩,等.改进的正弦余弦算法在函数优化问题中的研究[J].重庆理工大学学报(自然科学),2017(2):146-152. format:ZHANG Xiao-fei, BAI Yan-ping, HAO Yan, et al.Research of Improved Sine Cosine Algorithm in Function Optimization[J].Journal of Chongqing University of Technology(Natural Science),2017(2):146-152. 10.3969/j.issn.1674-8425(z).2017.02.024 TP301 A 1674-8425(2017)02-0146-073 仿真试验和结论



4 结束语

